4. La réponse à la sélection

Introduction au sujet

Dans ce chapitre, nous aborderons des notions de génétique quantitative. La compréhension du concept de réponse à la sélection et de ce qui l’affecte nous permettra de tester des prédictions sur l’évolution des adaptations physiologiques.

Objectifs spécifiques

À la fin de ce chapitre, vous serez en mesure de :

  • Expliquer l’objectif de la génétique quantitative
  • Définir la réponse à la sélection
  • Expliquer les variables qui forment l’équation de l’éleveur
  • Définir l’héritabilité
  • Appliquer une méthode pour estimer l’héritabilité

Notions clés

1. La génétique quantitative

En tant que biologistes, nous sommes intéressés à comprendre l’évolution des adaptations. Pour que ces adaptations évoluent, il doit y avoir présence de sélection naturelle dans une population, soit une différence de phénotype entre les individus qui est associée à une différence de fitness. Cependant, la présence de sélection naturelle n’est pas suffisante pour qu’il y ait évolution, qui, rappelons-le, est définie comme un changement de fréquences alléliques entre les générations. Pour qu’il y ait de la sélection naturelle, une corrélation entre la valeur d’un trait et le fitness est essentielle. Pour qu’il y ait réponse à la sélection, c’est-à-dire un changement de phénotype dans la prochaine génération comparé à la génération parentale, une corrélation entre la valeur du trait et le génotype doit aussi être présente. Si c’est le cas, il y a alors une corrélation entre le génotype et le fitness et un changement de fréquences alléliques entre les générations. Pour illustrer ce fait, nous allons utiliser des principes de la génétique quantitative.

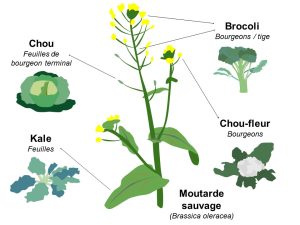
La génétique quantitative est un champ de recherche en biologie qui remonte aux programmes de sélection en agriculture, par exemple pour des plantes ou des animaux possédant certaines caractéristiques désirables comme une croissance rapide, une résistance à un pathogène, etc. Habituellement, on veut augmenter la valeur d’un trait (augmenter la quantité de gras d’un animal, augmenter la taille d’un légume) ou le diminuer (âge à la reproduction). On fait donc de la sélection directionnelle. Ainsi, comme nous l’avons vu, le graphique représentant la relation entre le phénotype et le fitness montre une relation linéaire. Si on prend l’exemple de la moutarde sauvage qui a été sélectionnée artificiellement en agriculture (figure 4.1), la cible de la sélection peut être les feuilles du bourgeon terminal, ce qui donne le chou, le bourgeon et les tiges, qui donnent le brocoli, les bourgeons, qui donnent le chou-fleur, ou bien les feuilles, qui donnent le chou kale.

Plant de moutarde sauvage (Brassica oleracea) dont différentes parties de la plante sont visées par la sélection artificielle afin de créer différents légumes tels que le chou (feuilles de bourgeon terminal), le kale (feuilles), le brocoli (bourgeons/tiges) et le chou-fleur (bourgeons).Figure 4.1. Sélection artificielle sur différents traits de la moutarde sauvage (Brassica oleracea) sur des centaines d’années, à l’origine de plusieurs légumes consommés de nos jours, tel le chou, le kale, le brocoli et le chou-fleur. Adapté de [1].

 

Les scientifiques dans ce domaine tentent de prédire quelle est la réponse à la sélection sur un trait donné, étant donné la pression de sélection artificielle qu’ils imposent en sélectionnant uniquement certains individus avec un phénotype désirable pour se reproduire. Ils ont développé un modèle pour quantifier la réponse à la sélection, c’est-à-dire s’il y a aura évolution à la suite de la sélection. Ce type d’approche nous intéresse, car cette façon de quantifier la réponse à la sélection dans un programme de croisements en agriculture nous permet aussi de comprendre l’évolution en milieu naturel, à court terme.

Cette vidéo présente un résumé sur la génétique quantitative. [CC-BY]

Vous trouverez la transcription de l’audio de cette capsule en cliquant sur ce lien: Transcription en format word

 

 

2. La réponse à la sélection

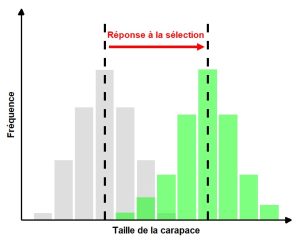
La réponse à la sélection peut être définie comme le changement de la moyenne et/ou de la variance du phénotype entre la génération parentale et la génération de leurs rejetons. La réponse à la sélection peut donc être quantifiée en utilisant le changement de la distribution de fréquence de la valeur des phénotypes dans une population entre les générations (figure 4.2).Histogrammes de fréquence de la taille de la carapace chez deux générations de tortues. La distribution de fréquence est décalée vers les valeurs plus élevées dans la génération des rejetons. Ainsi, la génération suivante possède en moyenne une taille de carapace plus élevée.Figure 4.2. Réponse à la sélection entre deux générations de tortues où les individus à grandes carapaces présentent un meilleur fitness. L’histogramme en gris représente la distribution parentale et l’histogramme en vert représente la distribution des rejetons.

 

3. L’équation de l’éleveur

Nous savons que la sélection naturelle est définie comme la relation entre le fitness et le phénotype et qu’on peut la quantifier pour un trait à l’intérieur d’une génération et obtenir le coefficient de sélection S. Cependant, comme nous l’avons déjà évoqué, ce coefficient de sélection S n’implique pas nécessairement un changement de phénotype entre les générations. Il peut y avoir de la sélection naturelle sans évolution! Pourquoi? Parce que la réponse à la sélection (R) à la prochaine génération (c.-à-d. l’évolution) dépend aussi d’un autre facteur, l’héritabilité du trait, désigné h2.

 

Ceci est représenté par l’équation de l’éleveur :

R = S * h2

 

La figure animée 4.3 illustre la contribution de la force de la sélection et de l’héritabilité du trait sur la réponse à la sélection.

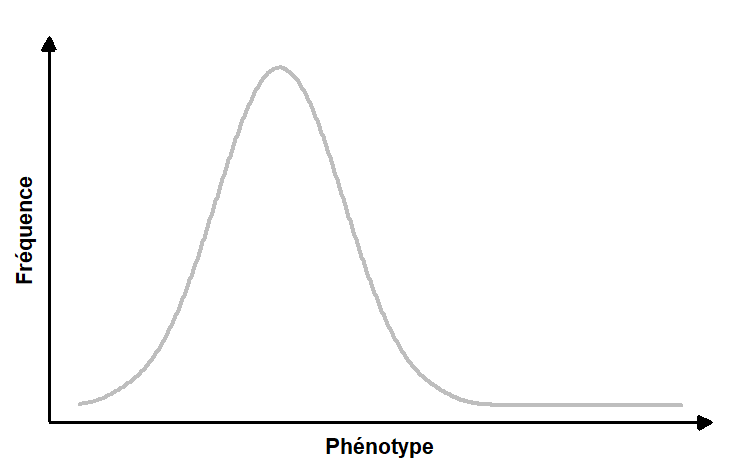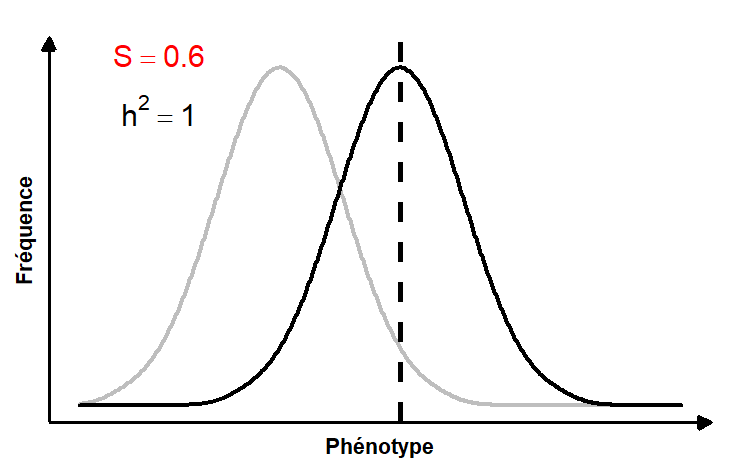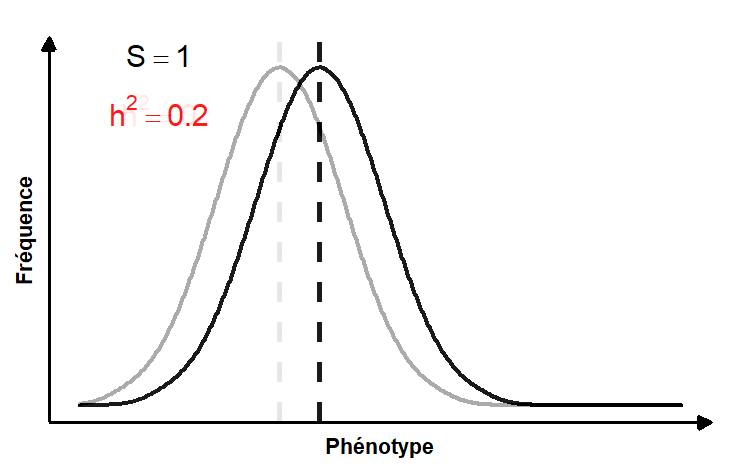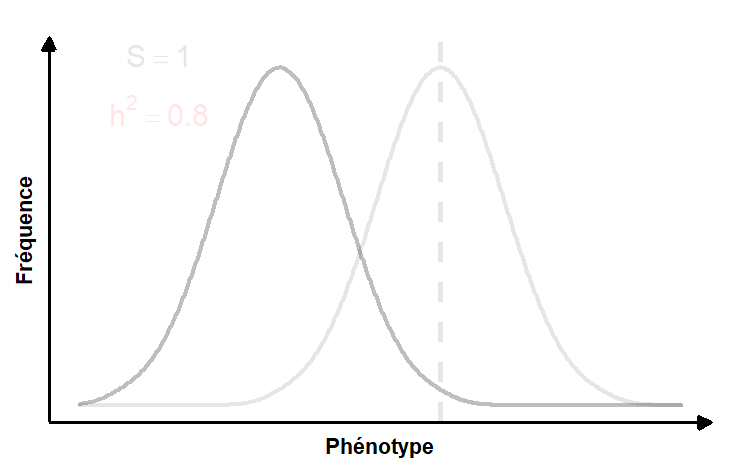
Graphique animé présentant le changement de la fréquence d’un phénotype, par la réponse à la sélection, causé par un changement des paramètres S ou h2. Le paramètre S est laissé constant à une valeur de 1 alors qu’on varie la valeur de h2 entre 0 et 0,8. La réponse à la sélection est d’abord nulle lorsque h2 est de zéro, mais augmente par la suite. La courbe se déplace vers la droite. De la même manière, le paramètre h2 est laissé constant à une valeur de 1 alors qu’on varie la valeur de S entre 0 et 0,8. La réponse à la sélection est d’abord nulle lorsque S est de zéro, mais augmente par la suite. La courbe se déplace vers la droite.

Figure 4.3. Effet du changement des paramètres de l’équation de l’éleveur sur la réponse à la sélection. La distribution de fréquence du phénotype est représentée en gris à la génération 0 et en noir à la génération 1. La réponse à la sélection est nulle si le coefficient de sélection S est de zéro ou si l’héritabilité du trait est nulle.

 

En remaniant cette équation, on peut aussi estimer l’héritabilité du trait, si on connait la force de la sélection (par exemple si on effectue de la sélection artificielle) et si on peut mesurer la réponse phénotypique obtenue à la génération suivante.

4. L’héritabilité

L’héritabilité représente la proportion de la variance phénotypique (VP) que l’on mesure dans un trait quantitatif entre les individus qui est expliquée par la variance génétique (VG) dans une population, à un moment donné.

 

Héritabilité au sens large : H2 = VG/VP

 

Nous n’avons pas à connaitre les bases génétiques de cette variation. La plupart du temps, on ne sait pas quel gène (pour les traits discrets), ou plus souvent quels gènes (pour les traits quantitatifs), affectent la valeur du trait et de quelle façon. On veut simplement savoir si les différences qu’on observe sont entièrement dues à l’environnement dans lequel les individus se sont développés (par exemple si certains ont eu accès à plus de nourriture que d’autres) ou si ces différences sont reliées à des différences dans leur génotype. En rappel, on peut représenter l’apport de la variation génétique et celui de la variation environnementale sur la variation phénotypique comme ceci :

VP = VG + VE

 

Autrement dit, on se demande si la variation génétique (VG) explique une grande partie de la variation phénotypique (VP), ce qui correspond à de l’héritabilité élevée, ou si au contraire la variation dans le phénotype est complètement due à l’environnement (VE), ce qui correspond à l’héritabilité proche de zéro ou carrément nulle. Dans la réalité, on est le plus souvent intéressé par l’héritabilité au sens strict (h2, remarquez qu’ici on utilise une lettre minuscule) qui quantifie l’apport de la variance génétique additive.

 

Héritabilité au sens strict : h2 = VG additive/VP

 

La variation génétique additive représente les effets additifs des allèles des différents locus et exclut les effets de dominance d’un allèle sur l’autre, un phénomène que nous avons déjà vu, ainsi que les interactions entre les allèles à différents locus ou entre les allèles à un locus, un phénomène appelé épistasie (voir figure 4.4 pour un exemple d’épistasie).

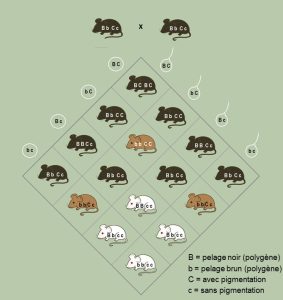
Échiquier de Punnett présentant les combinaisons d’allèles pour deux gènes affectant la coloration du pelage de la souris. L’allèle B code pour un pelage noir (polygène) alors que l’allèle b code pour un pelage brun (polygène). Le gène C a un effet épistatique puisqu’il permet l’expression des gènes de pigmentation. L’allèle C permet l’expression de la pigmentation alors que l’allèle c ne le permet pas. Les individus homozygotes cc sont alors albinos (blancs).Figure 4.4. Échiquier de Punnett présentant un cas d’épistasie affectant la couleur du pelage chez la souris. Si le gène de pigmentation (C) n’est pas produit, les autres gènes de couleur du pelage (B, b) n’ont pas d’effet sur le phénotype, qu’ils soient des génotypes dominants ou récessifs. Adapté de [2].

 

C’est donc une version très simple que nous utilisons. Si un trait est majoritairement influencé par l’effet d’un allèle à un locus sur un allèle à un autre locus (épistasie), ça ne sera pas capturé dans l’équation de l’éleveur. Comme ce sont les allèles qui sont transmis, et non les combinaisons d’allèles, l’équation de l’éleveur tente de mesurer la contribution des allèles et non la contribution de paires d’allèles entre des locus ou à un locus. Pour les éleveurs et éleveuses qui veulent faire de la sélection directionnelle, l’épistasie n’est pas « intéressante ». Cependant, ça peut l’être grandement pour des biologistes évolutifs! Nous nous contenterons en revanche de ce modèle plus simple afin d’explorer comment les traits physiologiques qui nous intéressent peuvent évoluer. Pour la suite du texte, nous utiliserons « héritabilité » pour parler de l’héritabilité au sens strict (h2).

Prenons un exemple de trait pour lequel nous avons une estimation de la variation phénotypique dans une population, soit la taille de la carapace d’une espèce de tortues (figure 4.5). Quelle est la cause de cette variation? Est-elle due à de la variation génétique (VP)? Est-ce un effet de l’environnement (VE)? Dans le cas d’une population de tortues, un effet environnemental sur la taille de la carapace pourrait être la température ambiante durant l’incubation dans le nid. Cette température pourrait varier selon la profondeur à laquelle la mère a creusé son nid. Ainsi, la variation dans le phénotype entre les individus serait entièrement explicable par la variance environnementale et l’héritabilité serait de zéro.Histogramme de fréquence de la taille de carapaces dans une population.Figure 4.5. Fréquence de la taille de carapace dans une population de tortues.

 

5. Estimer l’héritabilité en utilisant les parents et les rejetons

L’héritabilité mesure si on peut prédire le phénotype des rejetons à partir du phénotype des parents. Si on peut prédire de quoi aura l’air la prochaine génération (héritabilité élevée), ça veut dire que le génotype de l’individu (qui lui vient de ses parents) explique une très grande partie de son phénotype pour ce trait. Si on a une héritabilité élevée et que certains parents avec certains phénotypes se reproduisent davantage (il y a de la sélection), il y aura réponse à la sélection, car le phénotype des rejetons sera similaire à celui des parents qui se sont reproduits. Donc, pour un même coefficient de sélection S, la valeur d’héritabilité affecte la réponse à la sélection.

S’il y a une corrélation entre le phénotype moyen des deux parents et celui des rejetons, c’est qu’on peut prédire le trait des descendants à partir des parents. Le trait a donc une forte héritabilité. La pente de la corrélation est une estimation de l’héritabilité (figure 6). Une héritabilité de 1 voudrait dire que toute la variance phénotypique (VP) est expliquée par la variance génotypique (VG) et qu’on peut prédire la taille du rejeton avec la taille moyenne des deux parents. Une héritabilité de 0 veut dire que toute la variation observée est due à la variance environnementale (VE). Habituellement, on se retrouve avec des valeurs d’héritabilité entre ces deux valeurs. 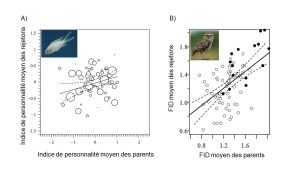Dans la figure 4.6, on voit un exemple où la pente est faible (panneau A, h2 = 0,12) et un autre ou la pente est élevée (panneau B, h2 = 0,64).Un graphique en nuage de point présente la relation entre la valeur moyenne d,un phénotype pour des rejetons et la moyenne de ce trait pour les parents. A) la pente de la relation entre l’indice de personnalité moyen des rejetons et des parents est faible, signifiant une faible héritabilité du trait chez ce poisson. B) La pente de la relation entre la distance moyenne d’initiation du vol des rejetons et des est élevée, signifiant une forte héritabilité du trait étudié chez cette espèce de hibou.Figure 4.6. Héritabilité d’un trait du comportement chez deux espèces. A) Indice de personnalité (audace, agressivité, propension à explorer) des rejetons de poissons Neolamprologus pulcher en fonction de celui de leurs parents. L’héritabilité de ce trait est faible (0,12). B) Distance d’initiation du vol (FID) des rejetons de Chevêche des terriers (Athene cunicularia) en fonction de celle de leurs parents. L’héritabilité de la crainte des humains est plutôt élevée (0,64). Adapté de [3-6].

 

Imaginons qu’il y a de la sélection sur un phénotype qui a une héritabilité élevée. Puisque certains individus vont avoir un meilleur fitness et comme l’héritabilité est élevée, les descendants auront une valeur de phénotype très similaire à leur parent, qui correspondent aux individus qui se sont reproduits. On pourra mesurer une réponse à la sélection dans la moyenne du trait dans la deuxième génération car la moyenne du trait qui nous intéresse changera entre la génération des parents et la génération des rejetons.

Cas appliqué

L’héritabilité mesurée en nature

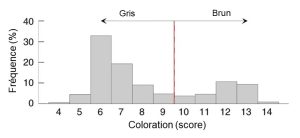
L’héritabilité peut être estimée en milieu naturel si on peut établir les liens de parenté entre des individus. Des scientifiques ont observé deux colorations distinctes chez une espèce de chouette hulotte, étant soit grises soit brunes (Strix aluco) (figure 4.7).

La coloration du plumage observées chez la chouette hulotte est bimodale: certains individus ont une grande proportion de gris dans leur plumage et d’autres sont plutôt bruns.Figure 4.7. Coloration du plumage chez la chouette hulotte observée au sud de la Finlande. Adapté de [7].

 

Les ornithologues ont quantifié précisément la variation phénotypique dans la coloration du plumage de cette chouette en mesurant la quantité de brun sur le plumage de 491 oiseaux. Elles ont mis en évidence une distribution bimodale du score de coloration (figure 4.8).L’histogramme de la distribution de fréquence du score de coloration brune a des valeurs allant de 4 à 14. La distribution est bimodale, avec 30% des individus ayant un score de coloration de 6, ce qui est considéré comme un morphe gris et un deuxième mode d’environ 10% pour le score de coloration 12, considéré comme un morphe brun. Les fréquences les plus basses sont autour des score de coloration 9 et 10, et les auteurs ont divisé les individus en un morphe ou l’autre en utilisant cette valeur comme séparation.Figure 4.8. Le score de coloration brune du plumage de chouettes présente une distribution bimodale. Adapté de [7].

 

Les biologistes ont estimé l’héritabilité de la coloration à l’aide de 187 paires de parent et de rejetons dont le suivi en nature a été fait grâce à de l’identification individuelle. Elles ont estimé l’héritabilité à h2 = 0.79. Ceci indique que presque 80% de la variation phénotypique de la coloration est expliquée par la variation génétique entre les individus. On peut donc prédire la coloration d’un rejeton à partir de celle de ses parents. La bimodalité des données leur a permis de modéliser avec une haute probabilité que le trait est contrôlé par un petit nombre de gènes qui ont de larges effets sur la coloration et qu’un individu hétérozygote serait brun, avec l’allèle brun dominant sur l’allèle gris.

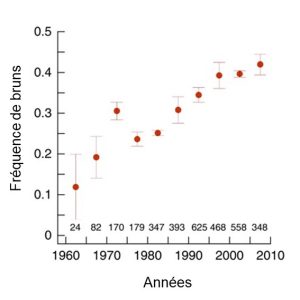
Des données obtenues depuis les années 1960 montrent que la proportion d’individus bruns a constamment augmenté dans les dernières décennies (figure 4.9). Comme l’héritabilité du trait est très élevée, les biologistes excluent la possibilité que ce soient des changements environnementaux qui aient affecté le phénotype (comme la diète). De plus, comme ce patron d’augmentation du morphe brun est retrouvé partout en Finlande et que la migration est faible, elles proposent que ce changement de fréquence n’est pas le résultat de la dérive génique ou du flux génique, mais plutôt le résultat de la sélection naturelle. Nous aurions alors dans cette figure un exemple de réponse à la sélection. Il reste aux biologistes à démontrer quel est l’agent de sélection et si la coloration est elle-même la cible de la sélection, ou si un autre trait est sous sélection.

La fréquence moyenne du morphe brun passe d’environ 10% en 1960 et augmente de façon graduelle jusqu’à une valeur de 40%dans les années 2000. Ce pourcentage d’individus bruns dans la population se maintient jusqu’en 2010.Figure 4.9. La fréquence d’individus avec une coloration brune a augmenté entre 1960 et 2010. Adapté de [7].

L’héritabilité calculée à l’aide de bases de données génétiques

Nous avons souvent vu des mesures d’héritabilité pour des phénotypes visibles à l’œil nu, comme la coloration du plumage. Il est cependant aussi possible de calculer l’héritabilité de phénotypes à d’autres niveaux d’organisation biologique. Des scientifiques travaillant en biologie médicale ont évalué l’héritabilité du niveau de métabolites sanguins chez des patients et des patientes à jeun. Les petites molécules qui sont produites durant le fonctionnement des cellules sont des métabolites, qui collectivement forment le métabolome. Ces scientifiques s’y intéressent chez les humains car ils veulent savoir si les différences de métabolome qu’on observe entre les individus sont liées à des différences de génotype, pour ensuite étudier si ces différences pourraient être la cause de maladies. Nous avons vu que l’on peut estimer l’héritabilité d’un trait en utilisant la relation entre les parents et les rejetons. Il est aussi possible d’estimer l’héritabilité en utilisant les données de gens apparentés, comme des jumeaux ou des frères et sœurs. Les bases de données pour les tests sanguins sont immenses dans plusieurs pays et permettent de faire ce genre d’estimé.

Les biologistes ont utilisé les données de métabolome sanguin et de génotype de 5117 personnes d’origine européenne qui faisaient partie au total de 2445 familles [8]. Ils ont estimé l’héritabilité du niveau de 369 métabolites et ont découvert que les mesures d’héritabilité varient entre les classes de métabolites. L’héritabilité est assez élevée pour les niveaux de lipides dans le sang, autour de h2 = 0.5. Ceci suggère que la variance phénotypique dans les niveaux de lipides est expliquée à 50% par la variation génétique dans cette population et l’autre moitié par les effets environnementaux. Comme pour toutes les mesures d’héritabilité, ces données sont vraies pour cette population seulement. En effet, si on étudiait une population dans une autre région du monde, les effets environnementaux et les génotypes pourraient être différents et donc donner des valeurs d’héritabilité différentes.

Résumé

La génétique quantitative est une sous-discipline de la biologie qui a été développée pour faciliter les programmes de sélection artificielle en agriculture. Les principes de la génétique quantitative s’appliquent aussi à l’étude de la micro-évolution des populations sauvages. Un principe fondamental de la génétique quantitative est la réponse à la sélection, soit le changement de la moyenne du phénotype entre deux générations lorsqu’on applique une certaine pression de sélection sur la génération parentale. La réponse à la sélection est quantifiée avec l’équation de l’éleveur, qui définit la réponse à la sélection comme étant le résultat de la force de sélection sur ce trait et de l’héritabilité du trait dans cette population et cet environnement. Cette équation nous permet de voir dans quelle circonstance il peut y avoir de la sélection naturelle dans une population mais aucun changement de fréquence allélique et de phénotype dans la génération suivante. En effet, la sélection naturelle ne résulte pas toujours en évolution, ceci dépend aussi de l’héritabilité du trait.

Activité de révision

Exercices

Révision sur la réponse à la sélection

 

Bibliographie

  1. Liwnoc (2019). Selective breeding enlarged desired traits of the wild mustard plant (Brassica oleracea) over hundreds of years, resulting in dozens of today’s agricultural crops [CC-BY-SA]. https://commons.wikimedia.org/wiki/File:Wild_Mustard_Plant_Selective_Breeding.svg
  2. Sciencia58 (2019). Example of epistasis in coat colour genetics: If no pigments can be produced the other coat colour genes have no effect on gene expression, no matter if they would be dominant or recessive, no matter if the individual is homozygous [CC0]. https://commons.wikimedia.org/wiki/File:Epistasis.png
  3. Chervet, N., M. Zöttl, R. Schürch, M. Taborsky et D. Heg (2011). Repeatability and heritability of behavioural types in a social cichlid [CC-BY]. International Journal of Evolutionary Biology, 2011, 1-15. https://doi.org/10.4061/2011/321729
  4. Carrete, M., J. Martínez-Padilla, S. Rodríguez-Martínez, N. Rebolo-Ifrán, A. Palma et J.L. Tella (2016). Heritability of fear of humans in urban and rural populations of a bird species [CC-BY]. https://www.nature.com/articles/srep31060#rightslink
  5. Refet’s Cosmos (2016). Neolamprologus pulcher (Daffodil) Daffodil [CC-BY]. http://refetali.akvaryum.com/daffodil_cp22972.asp
  6. Thompson, J. (2012). Borrowing Owl [CC-BY]. https://www.flickr.com/photos/79492850@N00/7700136498
  7. Karell, P., K. Ahola, T. Karstinen, J. Valkama et J.E. Brommer (2011). Climate change drives microevolution in a wild bird [CC-BY-NC-SA]. Nature Communications, 2(1), 208. https://doi.org/10.1038/ncomms1213
  8. Hagenbeek, F.A., R. Pool, J. Van Dongen, H.H.M. Draisma, J. Jan Hottenga, G. Willemsen, A. Abdellaoui, I.O. Fedko, A. Den Braber, P.J. Visser, E.J.C.N. De Geus, K. Willems Van Dijk, A. Verhoeven, H.E. Suchiman, M. Beekman, P.E. Slagboom, C.M. Van Duijn, A.C. Harms, T. Hankemeier, M. Bartels, M.G. Nivard et D.I. Boomsma (2020). Heritability estimates for 361 blood metabolites across 40 genome-wide association studies. Nature Communications, 11(1). https://doi.org/10.1038/s41467-019-13770-6

Licence

Symbole de License Creative Commons Attribution - Pas d’utilisation commerciale - Partage dans les mêmes conditions 4.0 International

Écophysiologie évolutive  Copyright © 2024 by Nadia Aubin-Horth is licensed under a License Creative Commons Attribution - Pas d’utilisation commerciale - Partage dans les mêmes conditions 4.0 International, except where otherwise noted.

Partagez ce livre