8 Comment se déplacer ? Contrôle, navigation et planification de trajectoire pour les robots mobiles
Jiefei Wang and Damith Herath
Table des matières
Une perspective de l’industrie : Entrevue avec Dana Leslie, ancienne employée de Clearpath Robotics
8.3.1.1 Modélisation cinématique
8.3.1.2 Propulsion holonomique
8.3.1.6 Roues omnidirectionnelles
8.3.2.4 Robots à quatre pattes
8.3.3.2 Un exemple de quadrirotor
8.4.1 Régulateurs PID (proportionnel, intégral et dérivé)
8.4.1.1 Contrôle proportionnel (P)
8.4.1.4 Réglage d’un régulateur PID
8.4.2 Régulateurs à logique floue
8.5 Planification de trajectoire
8.5.1 Algorithmes heuristiques de planification de chemin
8.5.2 Algorithmes probabilistes de planification de chemin
8.6.2 L’histogramme de champ vectoriel (VFH)
8.1 Objectifs d’apprentissage
Vous en apprendrez plus sur :
- Les contrôleurs et techniques de contrôle utilisés en robotique, y compris le régulateur PID
- Les types de locomotion des robots mobiles
- La planification de la trajectoire de robot et évitement d’obstacles.
8.2 Introduction
Lorsque nous pensons aux robots, nous les imaginons comme des manipulateurs, soit dans des installations de fabrication où ils sont stationnaires, soit comme des robots mobiles qui se déplacent (Figure 8-1). Les robots qui se déplacent dans l’environnement sont appelés robots mobiles. Ce chapitre examine les robots mobiles, comment les contrôler, les différents types de locomotion et les algorithmes utilisés pour planifier les trajectoires et l’évitement des obstacles lors de la navigation.
Figure 8-1 : Un bras de robot Kinova Gen3 lite monté sur une plate-forme robotique mobile Clearpath Dingo Indoor (à gauche) à côté d’un véhicule terrestre sans pilote Jackal utilisé pour la navigation en extérieur. (à droite) (Crédits Clearpath/Kinova)
Une perspective de l’industrie
Entrevue avec Dana Leslie, ancienne employée de Clearpath Robotics
Comme beaucoup de jeunes ingénieurs, je suis reconnaissante envers mes parents de m’avoir encouragée à explorer le monde de la robotique. Dès mon plus jeune âge, le plaisir de jouer avec des lego, des kits électroniques et la programmation informatique, a certainement été le moteur de mon choix de carrière en tant qu’ingénieur.
Après avoir obtenu mon diplôme en génie électrique de l’Université de Victoria, j’ai eu la chance de commencer ma carrière dans l’industrie en obtenant un poste chez Cellula Robotics, une entreprise spécialisée dans la robotique sous-marine. C’est là où notre équipe a développé des robots, les a construits et les a déployés dans les zones les plus profondes de l’océan, étudiant et découvrant le monde sous-marin.
Des fonds marins à la terre, les robots que j’ai contribué à concevoir ont continué d’évoluer; j’ai travaillé sur le développement de systèmes terrestres à roues chez Clearpath Robotics en Ontario et, plus récemment, sur des humanoïdes à pattes chez Agility Robotics en Oregon.
Pour la conception d’un robot mobile, nous avons inclus des diodes dans le système d’alimentation, ce qui permet un remplacement à chaud de la batterie. Toutefois, cela signifie que l’énergie produite par la force contre-électromotrice des moteurs lorsque ceux-ci freinent ou sont poussés, ne peut pas être absorbée par la batterie. Le résultat a été une augmentation incontrôlée de la tension, ce qui a causé des problèmes dans différents sous-systèmes, et finalement conduit à l’arrêt total du robot.
Ce type de défi est simple à conceptualiser, mais beaucoup plus difficile à quantifier. Cette situation n’est observable que dans un système totalement intégré, elle est liée à des éléments indépendants de notre volonté et s’accentue lors du transport de charges lourdes ou de la descente de rampes. (Augmentation de la conversion de l’énergie mécanique en énergie électrique.)
En fin de compte, après des tests exhaustifs et répétitifs, la solution consistait en une combinaison de réduction des taux de décélération, de modification de la capacité du système et de l’utilisation de diodes de suppression de tension transitoire.
Il est important de pouvoir alimenter votre robot en lui donnant une poussée, mais il est essentiel que votre robot réagisse lorsqu’il doit s’arrêter!
Les avancées en matière de détection embarquée, de traitement, d’électronique de puissance et de chimie des batteries ont contribué au progrès de l’industrie de la robotique au cours de ma carrière.
Des servo-actionneurs précis et à haute densité d’énergie ont récemment permis le développement de robots humanoïdes de pointe qui sont sur le point de transformer le monde du travail en automatisant les tâches les plus ennuyeuses et les plus dangereuses effectuées par les humains.
Grâce à ces actionneurs, la manipulation robotique a atteint un niveau avancé, ce qui permet à la technologie d’aller au-delà des lignes de production et de s’intégrer sur les lignes de front. Les bras robotiques ne sont plus uniquement utilisés pour l’assemblage de voitures, mais également pour retourner des hamburgers ou emballer vos courses!
8.3 Robots mobiles
Au cours des dernières décennies, les robots mobiles ont suscité un grand intérêt en raison de leur capacité à explorer des environnements complexes tels que l’espace, les opérations de sauvetage et à effectuer des tâches de manière autonome, sans intervention humaine. On peut largement classer les robots mobiles en deux catégories : les robots à roues et les robots volants.
8.3.1 Robots à roues
Les robots à roues se déplacent sur le sol en utilisant des roues motorisées pour se propulser. Comparativement aux robots qui utilisent des pattes ou des ailes pour se déplacer sur un terrain plat ou rocheux, ils sont plus faciles à concevoir, construire et utiliser. De plus, leur contrôle est plus facile, car ils ont moins de degrés de liberté que les robots volants. Toutefois, l’un des défis des robots à roues est qu’ils ne peuvent pas fonctionner de manière optimale sur certaines surfaces du sol telles que les fortes pentes, les terrains accidentés ou les zones à faible friction. Cependant, les robots à roues sont les plus répandus sur le marché grand public en raison de leur faible coût et de la simplicité de leurs mécanismes de direction différentiels. Même si ces robots peuvent avoir n’importe quel nombre de roues, les mécanismes doivent être modifiés pour maintenir l’équilibre dynamique en fonction du nombre de roues. Les configurations à trois ou quatre roues sont les plus populaires et suffisent pour l’équilibre statique et dynamique parmi tous les robots à roues utilisés largement dans les projets de recherche.
8.3.1.1 Modélisation cinématique
Ce livre se concentre principalement sur deux types de robots et leurs mouvements : les robots mobiles et les robots à bras. Dans les deux cas, il est crucial de comprendre comment les mouvements produits par les actionneurs se traduisent en mouvements complexes du corps. Pour concevoir un robot capable d’interagir avec son environnement, nous devons comprendre ces relations géométriques de mouvement.
La Cinématique est l’étude des mouvements de points, de corps et de systèmes de corps (tels que les robots) sans tenir compte des forces agissant sur ces systèmes. Dans ce chapitre, nous discuterons de certaines configurations de roues courantes et de leurs modèles cinématiques respectifs utilisés dans les robots mobiles qui utilisent des moteurs pour les propulser. Ensuite, le chapitre 10 approfondira la modélisation de la cinématique des robots de type bras.
8.3.1.2 Propulsion holonomique
Le terme « holonomique » se rapporte à la relation entre les degrés de liberté contrôlables et totaux d’un robot. Si le nombre de degrés de liberté contrôlables est égal au nombre total de degrés de liberté, alors le robot est dit holonomique. Un exemple d’un tel système est un robot doté de roulettes ou de roues omnidirectionnelles pour la propulsion holonomique. Il peut se déplacer librement dans toutes les directions et les degrés de liberté contrôlables sont égaux aux degrés de liberté totaux.
En revanche, si le nombre de degrés de liberté contrôlables est inférieur au nombre total de degrés de liberté, le système est qualifié comme non-holonomique. Par exemple, une voiture dispose de trois degrés de liberté : sa position selon deux axes et son orientation. Cependant, il n’y a que deux degrés de liberté contrôlables : l’accélération (ou le freinage) et l’angle de braquage du volant. Cela rend difficile pour le conducteur de tourner la voiture dans n’importe quelle direction (sauf si elle dérape ou glisse).
Pour un robot à entraînement différentiel typique, (se référer à Figure 8-4) la contrainte non holonomique pourrait s’écrire comme ceci :
| [latex]\begin{equation} \dot{x} \sin (\phi)-\dot{y} \cos (\phi)=0 \end{equation}[/latex] | (8.1) |
8.3.1.3 Robots à trois roues
L’une des configurations d’actionneurs les plus courantes pour entraîner un robot mobile est la configuration à trois roues (également connue sous le nom de modèle tricycle).
Il existe deux types de robots à trois roues :
- À direction différentielle – deux roues motrices séparées avec une roue supplémentaire à rotation libre. Pour modifier la direction d’un robot, il suffit de changer la vitesse de rotation relative de ses deux roues entraînées séparément. Si les deux roues tournent dans le même sens et à la même vitesse, le robot avancera tout droit. En revanche, si les deux roues tournent à des vitesses différentes ou dans des directions opposées, le robot se déplacera dans une direction différente en fonction de la combinaison de la vitesse et de la direction de rotation. (Figure 8-2)
- Ce type de robot est équipé de deux roues actionnées par un seul actionneur et d’un volant assisté.
Pour éviter tout déséquilibre, le centre de gravité de ce robot doit se trouver à l’intérieur du triangle formé par les roues. Si trop de poids est réparti du côté de la roue en rotation libre, cela peut causer un déséquilibre et entraîner le basculement du robot.
Figure 8-2 : Robot à trois roues à direction différentielle. Les deux roues avant (en haut) sont alimentées par deux moteurs à courant continu. La roue pivotante arrière est libre de tourner et n’est pas alimentée.
Maintenant, explorons comment modéliser cinématiquement un robot à trois roues à direction différentielle.
Le modèle présenté dans la Figure 8-3, introduit une roue virtuelle pour l’ensemble avant de roues motrices différentielles. Les deux roues le long de la ligne médiane du robot représentent essentiellement l’ensemble du système. Avec lesdites contraintes, le robot ne peut exercer que deux degrés de liberté. Ainsi, la dérivation du modèle cinématique fait référence au modèle simplifié du robot. Le centre de rotation instantané (également connu sous le nom centre de vitesse instantanée) dans ce modèle désigne un point fictif attaché au robot où, à un certain moment, la vitesse est nulle alors que le reste du corps du robot est en mouvement planaire. Vous pouvez imaginer que le robot tourne autour de ce point à l’instant considéré.
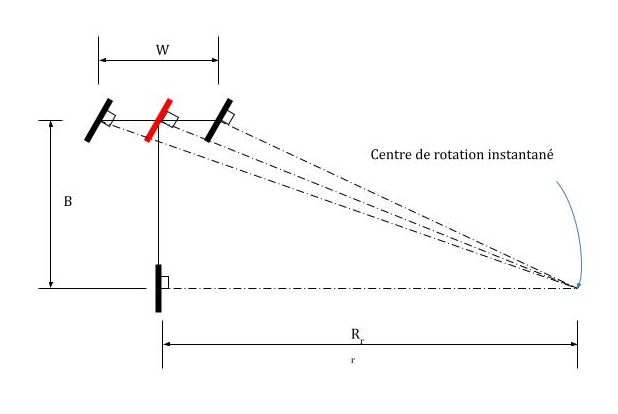
Figure 8-3 : Géométrie du véhicule d’un robot à trois roues typique
Il est possible de dériver la forme temporelle continue du modèle de véhicule (par rapport au centre de la roue avant) de la manière suivante :
| [latex]\begin{equation} \dot{x}(t)=V(t) \cos (\phi(t)+\gamma(t)) \end{equation}[/latex] | (8.2) |
| [latex]\begin{equation} \dot{y}(t)=V(t) \sin (\phi(t)+\gamma(t)) \end{equation}[/latex] | (8.3) |
| [latex]\begin{equation} \dot{\varphi}(t)=\frac{V(t) \sin (\gamma(t)}{B} \end{equation}[/latex] | (8.4) |
Où [latex]x(t)[/latex] et [latex]y(t)[/latex] désignent la position du véhicule, l’angle [latex]\phi(t)[/latex] est l’orientation du robot par rapport à l’axe x, et [latex]V(t)[/latex] représente la vitesse linéaire de la roue avant. L’angle [latex]\gamma[/latex] est défini comme l’angle de braquage du véhicule. B est la longueur de base entre les deux ensembles de roues.
Un modèle cinématique plus simple peut être dérivé du modèle discuté précédemment dans de nombreuses configurations de robot simples où le système rend la vitesse du robot [latex]V(t)[/latex] et la vitesse angulaire du robot [latex]\dot{\phi}(t)[/latex] directement disponibles (par exemple via des encodeurs à roue). Ensuite, le modèle de processus pour le système correspondant peut être représenté comme suit :
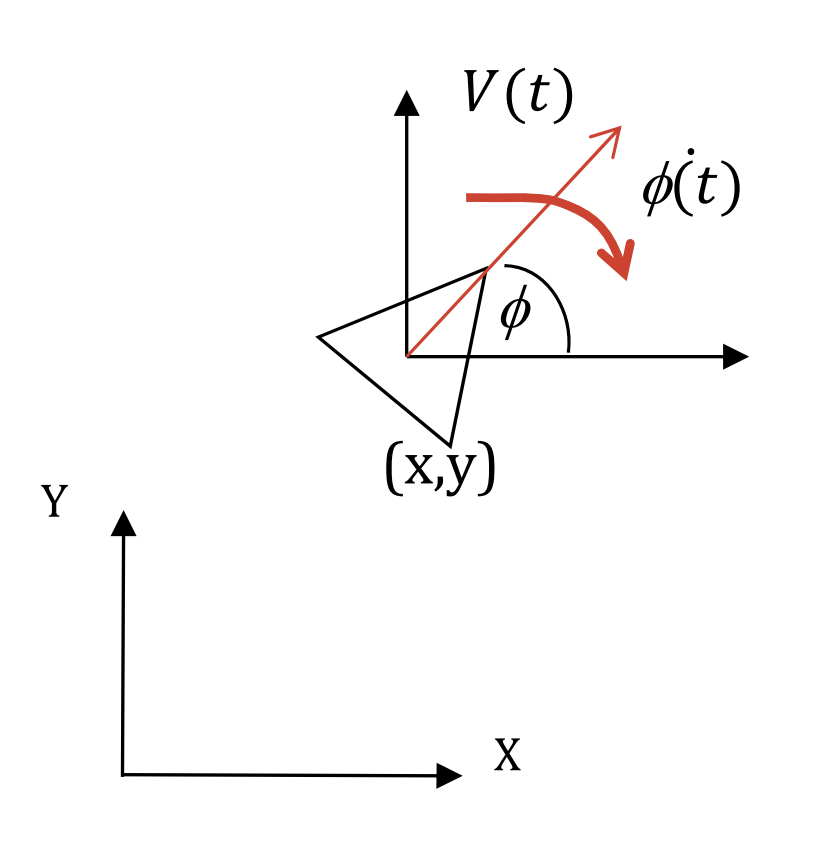
Figure 8-4 : Modèle de robot simplifié
Les équations suivantes plus simples peuvent alors être dérivées :
| [latex]\begin{equation} \dot{x}(t)=V(t) \cos (\phi(t)) \end{equation}[/latex] | (8.5) |
| [latex]\begin{equation} \dot{y}(t)=V(t) \sin (\phi(t)) \end{equation}[/latex] | (8.6) |
| [latex]\begin{equation} \dot{\varphi}(t)=\omega (t) \end{equation}[/latex] | (8.7) |
8.3.1.4 Robots à deux roues
Les robots à deux roues sont plus difficiles à équilibrer que les autres types, car ils doivent continuer à bouger pour rester debout. Le centre de gravité du corps du robot est maintenu sous l’essieu. Généralement, cela est accompli en plaçant les piles sous le corps du robot. Les roues peuvent être parallèles les unes aux autres, et ces véhicules sont appelés des dicycles, ou avoir une roue devant l’autre, comme les vélos avec les roues placées en tandem. Les robots à deux roues doivent continuellement se déplacer pour rester en équilibre, en avançant dans la direction où le robot se penche. Pour maintenir l’équilibre, la base du robot doit rester sous son centre de gravité. Pour un robot qui a des roues à gauche et à droite, il a besoin d’au moins deux capteurs. Un capteur d’inclinaison est utilisé pour déterminer l’angle d’inclinaison et les encodeurs de roue qui gardent une trace de la position de la plate-forme du robot.
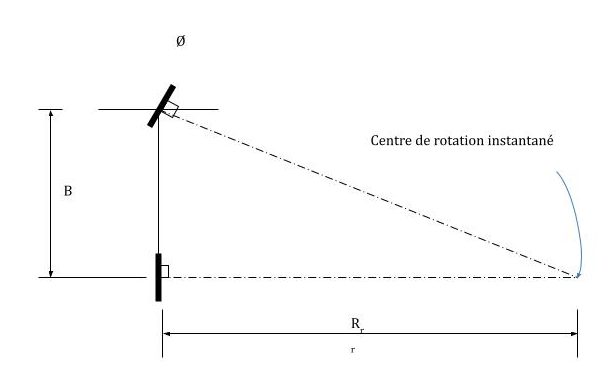
Figure 8-5 : Configuration des roues d’un robot à deux roues
Où [latex]\begin{equation} R_{r r}=\frac{B}{\tan \phi}, \alpha+\phi+90^{\circ}=180^{\circ} \end{equation}[/latex]
8.3.1.5 Robots à quatre roues
Il existe plusieurs configurations possibles avec quatre roues.
- Deux roues motorisées et deux roues en rotation libre
Ces robots ont deux roues à rotation libre supplémentaires pour améliorer l’équilibre, mais leur direction est toujours différentielle, similaire aux robots mentionnés précédemment.
Les robots à quatre roues sont plus stables que ceux à trois roues, car leur centre de gravité doit rester à l’intérieur d’un rectangle formé par les quatre roues au lieu d’un triangle. Cependant, il est conseillé de maintenir le centre de gravité au milieu du rectangle, car cela offre la configuration la plus stable, surtout lors de virages serrés ou sur une surface irrégulière.
- Roues motrices deux par deux pour un mouvement semblable à celui d’un char
Ce type de robot utilise deux paires de roues motrices, et chaque paire tourne dans le même sens. La partie délicate de ce type de propulsion est de faire tourner toutes les roues à la même vitesse. Si les roues d’une paire ne tournent pas à la même vitesse, la paire la plus lente patinera. Si les paires ne fonctionnent pas à la même vitesse, le robot ne peut pas rouler tout droit. Une bonne conception doit incorporer une certaine forme de direction semblable à celle d’une voiture.
- Direction semblable à celle d’une voiture (Entraînement Ackerman)
Cette méthode permet au robot de tourner de la même manière qu’une voiture (Figure 8-6). Toutefois, ce système présente un avantage par rapport aux méthodes précédentes, car le robot ne nécessite qu’un moteur pour entraîner les roues arrière et un servomoteur pour la direction. Les méthodes précédentes exigeaient soit deux moteurs, soit une boîte de vitesses très complexe comportant deux axes de sortie avec des vitesses et des directions de rotation indépendantes.
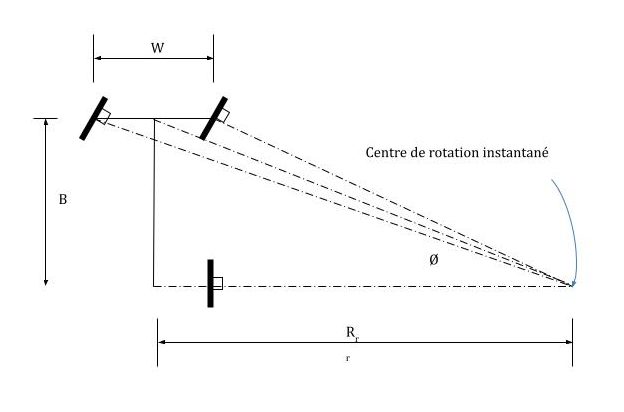
Figure 8-6 : Entraînement Ackerman
Où [latex]\begin{equation} R_{r r}=\frac{B}{\tan \phi} \end{equation}[/latex]
8.3.1.6 Roues omnidirectionnelles
Les robots à roues omnidirectionnels (Omni) appartiennent à une classe de robots mobiles non conventionnels.
Figure 8-7 : Un ensemble de roues Mecanum (un type de roue Omni) sur un robot domestique.
Une roue Omni est composée de nombreuses petites roues qui forment une grande roue, et les plus petites sont montées en angle par rapport à l’axe de la roue principale. Cette configuration permet aux roues de se déplacer dans deux directions et de se déplacer de manière holonomique, c’est-à-dire qu’elles peuvent instantanément se déplacer dans n’importe quelle direction, contrairement à une voiture qui se déplace de manière non holonomique et doit être en mouvement pour changer de direction. De plus, les robots à roues Omni peuvent se déplacer à n’importe quel angle dans n’importe quelle direction sans rotation préalable. Certains robots à roues Omni utilisent une plate-forme triangulaire, avec les trois roues espacées à des angles de 60 degrés. Les roues Omni présentent l’avantage de faciliter la conception de robots avec des roues montées sur un axe non aligné. L’utilisation de roues Omni présente toutefois un inconvénient majeur : leur efficacité est faible, car toutes les roues ne tournent pas dans le sens du mouvement, ce qui engendre une perte d’énergie par frottement. De plus, leur utilisation est plus complexe en termes de calculs, en raison des angles de mouvement qui doivent être pris en compte.
8.3.2 Robots marcheurs
Les robots à pattes tirent leur inspiration des êtres humains, des animaux ou des insectes, qui utilisent des mécanismes de pattes pour la locomotion. En comparaison aux robots à roues, ils sont plus polyvalents. Ils sont capables de se mouvoir dans des environnements extrêmes tels que des terrains non structurés, accidentés, inégaux, ou encore des espaces confinés complexes comme des environnements souterrains ou des structures industrielles.
Les robots à pattes peuvent être classés en fonction du nombre de membres qu’ils utilisent. Les robots avec un nombre de pattes plus élevé ont tendance à être plus stables, alors que ceux avec moins de pattes sont plus maniables. Pour maintenir son équilibre, un robot à pattes doit garder son centre de gravité à l’intérieur de son polygone de stabilité. Le polygone de stabilité est la surface plane délimitée par les points de contact entre les pattes et le sol. Ces pattes à plusieurs degrés de liberté sont généralement modélisées comme des chaînes cinématiques, comme décrit au Chapitre 10.
8.3.2.1 Démarche de robot
Le mouvement périodique des pattes du robot en contact avec le sol est appelé la démarche du marcheur. La démarche spécifique dépend de la configuration des pattes du robot, ainsi que de paramètres tels que la vitesse, le terrain, la tâche à accomplir et les limitations de puissance du robot. Milton Hildebrand a été l’un des premiers zoologistes à étudier les démarches des animaux. Depuis, plusieurs chercheurs ont adopté sa méthode pour spécifier les modèles de marche en robotique, offrant ainsi une approche formelle pour étudier et améliorer la démarche des robots.
8.3.2.2 Robots à deux pattes
Les robots à deux pattes sont aussi appelés des robots bipèdes. Les robots bipèdes sont confrontés à des défis fondamentaux tels que la stabilité et le contrôle du mouvement, qui englobent l’équilibre et la maîtrise des mouvements. Dans les systèmes avancés, des accéléromètres ou gyroscopes fournissent une rétroaction dynamique pour contrôler l’équilibre. Ces capteurs sont également utilisés pour le contrôle des mouvements, la marche, le saut et même la course, combinés à des technologies telles que l’apprentissage machine. D’autre part, le marcheur passif est un mécanisme bipède qui « marche » sans actionnement, utilisant simplement la gravité comme source d’énergie.
8.3.2.3 Robots humanoïdes
Si vous fermez les yeux et pensez à un robot, qu’imaginez-vous dans votre esprit ? Très probablement une créature fictive comme Arnold Schwarzenegger dans les films de la série Terminator ou C-3PO de Star Wars. Il s’agit vraisemblablement d’un humanoïde– un robot humanoïde avec une tête et un corps avec des bras et des jambes, probablement peint en argent métallique. On s’attend à ce que les robots humanoïdes imitent le mouvement et l’interaction humains. (Figure 8-9) Ils ont leurs racines dans le désir et la création de mythes, comme nous l’avons vu dans notre premier chapitre. Après des années de recherche, ils sont désormais disponibles sur le marché dans divers domaines d’application, notamment dans le domaine des jeux compétitifs (tels que la ligue humanoïde RoboCup [1]), ainsi que dans celui des robots sociaux et interactifs comme Pepper. (Figure 8-9) par Softbank Robotics. À proprement parler, Pepper est un robot semi-humanoïde avec une base de robot à roues et non un robot bipède. Comme mentionné précédemment, un robot à roues est beaucoup plus simple, stable et économique à produire. La façon dont ces robots sont déployés est en constante expansion, et avec le développement de nouvelles technologies, le marché suivra.
 |
 |
Figure 8-9 : Robot Pepper (à gauche) – un robot semi-humanoïde à roues utilisé dans le marketing de détail. Le HRP-1 (à droite) – un premier prototype de robot humanoïde développé par le National Institute of Advanced Industrial Science and Technology (AIST), du Japon, exposé au public dans ses locaux.
8.3.2.4 Robots à quatre pattes
Les robots à quatre pattes sont aussi appelés des robots quadrupèdes. Comparativement aux robots à deux pattes, ils présentent une stabilité améliorée lors de leurs mouvements. De plus, grâce à un centre de gravité plus bas et à leurs quatre pattes, ils conservent un équilibre solide lorsqu’ils sont immobiles. Ils peuvent se déplacer en déplaçant une patte à la fois ou en utilisant une autre paire de pattes.
Figure 8-10 : Le chien robot Sony Aibo – L’une des premières versions de la série de chiens robots à quatre pattes de Sony.
Types de démarche pour les robots à quatre pattes
Les robots à quatre pattes peuvent présenter des démarches statiquement et dynamiquement stables. Dans la démarche statiquement stable, chaque patte du robot est soulevée de manière séquentielle, de haut en bas, de sorte qu’il y ait toujours au moins trois pattes en contact avec le sol à tout moment. Ce type de démarche est connue sous le nom de démarche rampante (D Zhao, X Jing, 2012). Les démarches dynamiquement stables sont souvent utilisées dans les robots à quatre pattes pour marcher et courir en raison de leur efficacité, comme le trot, le rythme, le rebond et la démarche au galop (Y Fukuoka, H Kimura, 2009). Dans la démarche de trot, deux pattes du robot se trouvent en diagonale à la même hauteur, tandis que les deux autres pattes restent en contact avec le sol jusqu’à ce que les premières se soulèvent. Cette séquence se répète ensuite deux par deux selon un ordre précis.
8.3.2.5 Robots à six pattes
Les robots à six pattes sont aussi appelés des robots hexapodes. Ils sont conçus pour imiter la mécanique de marche des insectes. Leurs jambes se déplacent en forme de « vague » de l’arrière vers l’avant. Les robots hexapodes offrent une stabilité accrue lors de leurs déplacements et en position debout. De plus, ces robots peuvent fonctionner sur trois pattes tandis que les trois autres pattes restantes offrent de la flexibilité et accroissent leurs capacités. Dans les Chapitres 12 et 17, vous pourrez explorer la conception et la mise en œuvre d’un robot hexapode (Figure 8-11).
Types de démarche pour les robots à six pattes
Une par une est la démarche la plus simple, qui fait avancer chaque patte l’une après l’autre dans le sens des aiguilles d’une montre ou dans le sens inverse des aiguilles d’une montre tandis que les cinq pattes restantes sont dans la phase de posture – immobiles. Pour une démarche à quatre pattes (Figure 8-11), le robot déplace ses deux pattes avant (1 et 2) vers l’avant tandis que les quatre autres pattes (3, 4, 5, 6) soutiennent son corps. Ensuite, le robot déplace ses deux pattes centrales (3, 6) pour pousser le corps vers l’avant, tandis que les autres pattes (1, 2, 4, 5) continuent de le soutenir. Enfin, le robot balance ses deux dernières pattes (4 et 5) vers l’avant, tandis que les autres pattes (1, 2, 3, 6) continuent de le supporter. La séquence est ensuite répétée. Le démarche tripode utilise deux pattes d’un côté et une autre de l’autre côté (par exemple 1, 5 et 3), comme dans un trépied, pour maintenir le robot stable tout en déplaçant les trois pattes restantes vers l’avant (2, 4 et 6) ensemble.
Figure 8-11 : Un robot hexapode (Crédit Bryce Cronin).
8.3.2.6 Robots à huit pattes
Les araignées et autres arachnides inspirent les robots à huit pattes. Les robots octopodes offrent la plus grande stabilité parmi les robots à pattes, ce qui les rend particulièrement adaptés aux environnements difficiles, tels que les zones dangereuses où ils peuvent être utilisés pour effectuer des reconnaissances, détecter des dommages structurels et effectuer des tâches de maintenance.
8.3.3 Robots volants
De nombreux efforts ont été déployés pour améliorer l’endurance de vol et la charge utile des véhicules aériens sans pilote (UAV), plus communément appelés drones. Cela a conduit à la création de différentes configurations de drones de tailles, capacités et durées de vol variables. Contrairement aux robots à pattes et à roues, les robots volants sont libres d’utiliser les six degrés de liberté, permettant différents types de vol pour un drone. Ceux-ci sont connus sous le nom de lacet, tangage et roulis (Figure 8-12).
Lacet (ψ) – Il s’agit de la rotation de la tête du drone vers la droite ou vers la gauche. C’est le mouvement de base pour faire tourner le drone. Dans un drone piloté à distance, cela est généralement réalisé à l’aide de la manette des gaz gauche en se déplaçant vers la gauche ou la droite.
Tangage (θ) – Il s’agit du mouvement du drone, soit vers l’avant, soit vers l’arrière. En général, le mouvement de tangage vers l’avant dans un drone télécommandé est obtenu en poussant la manette des gaz vers l’avant, ce qui incline le drone vers l’avant et le fait avancer loin de vous. De même, le mouvement de tangage vers l’arrière est obtenu en tirant la manette des gaz vers l’arrière.
Roulis (Ø)– Le roulis fait voler le drone latéralement vers la gauche ou vers la droite. La manette des gaz de droite contrôle le roulis dans un drone piloté à distance.
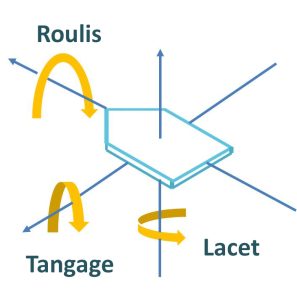
Figure 8-12 : Roulis, tangage et lacet.
Figure 8-13 : Différents types de multicoptères (dans le sens des aiguilles d’une montre à partir du haut à gauche – un quadrirotor – DJI MAVIC PRO, un hexacoptère – modèle sur mesure, DJI Phantom Model et un octocoptère – Modèle sur mesure)
8.3.3.1 Multicoptères
Un multicoptère est un type de véhicule volant avec des hélices entraînées par des moteurs (Figure 8-13). Les pales du rotor principal génèrent une force de poussée puissante qui est utilisée à la fois pour soulever et propulser le véhicule. Les véhicules aériens sans pilote multirotors sont capables de décoller et d’atterrir verticalement (VTOL) et peuvent maintenir une position de vol stationnaire à un endroit fixe, contrairement aux aéronefs à voilure fixe. Leur capacité de vol stationnaire et leur capacité à maintenir leur vitesse les rendent idéaux pour une utilisation civile, la surveillance, la reconnaissance et la photographie aérienne. Cependant, l’un des défis des multicoptères est qu’ils consomment plus d’énergie, ce qui réduit leur endurance. De plus, les multicoptères, contrairement à leurs homologues à voilure fixe, sont intrinsèquement aérodynamiquement instables et nécessitent un contrôleur de vol embarqué (un pilote automatique) pour maintenir la stabilité.
Les multicoptères peuvent être divisés en catégories spécifiques en fonction du nombre et du positionnement des moteurs, et chaque catégorie a sa propre mission (Figure 8-14). Et en fonction des exigences de la mission, ils sont classés dans diverses configurations telles que Monocoptère (1 rotor), tricoptère (3 rotors), quadricoptère (4 rotors), hexacoptère (6 rotors) configurations X/+), Octacoptère (8 rotors) (configurations X/+, rotor X8 et rotor Y6. Les quadrirotors, également appelés drones à quatre rotors, sont des hélicoptères multirotors équipés de quatre rotors qui assurent leur portance et leur propulsion. Ces appareils constituent des outils précieux pour les chercheurs universitaires qui souhaitent tester et évaluer de nouvelles idées dans des domaines variés tels que la théorie de commande de vol, la navigation, ou encore les systèmes en temps réel.
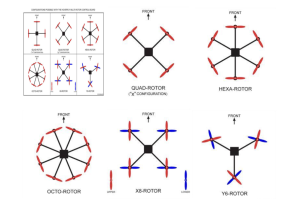
Figure 8-14 : Diverses configurations sont possibles avec la carte de commande hoverfly multirotor (Ed Darack, 2014)
8.3.3.2 Un exemple de quadrirotor
Un quadrirotor (drone) est capable d’effectuer trois manœuvres dans le plan vertical : vol stationnaire, montée ou descente.
Vol stationnaire – Pour maintenir une position fixe en vol, les quatre rotors produisent une poussée nette qui doit être égale à la force gravitationnelle qui tire le drone vers le bas.
Ascension – Pour monter en altitude, la poussée (vitesse) des quatre rotors est augmentée de manière à ce que la force vers le haut soit supérieure au poids et à l’attraction gravitationnelle.
Descente – Pour descendre, il faut faire exactement le contraire de l’ascension, c’est-à-dire réduire la poussée (vitesse) des rotors de manière à ce que la force nette soit dirigée vers le bas.
Afin de faire avancer un quadricoptère, il est nécessaire d’augmenter la vitesse de rotation des rotors 3 et 4 (situés à l’arrière) tout en diminuant celle des rotors 1 et 2 (à l’avant). Il est important que la force de poussée totale reste égale au poids du drone pour qu’il conserve son niveau vertical. Pour effectuer une rotation sans déséquilibrer le drone, il est nécessaire de diminuer la vitesse de rotation des rotors 1 et 3, tout en augmentant celle des rotors 2 et 4.
Figure 8-15 : Une configuration de rotor de quadricoptère.
Modèle mathématique d’un quadricoptère
La structure du quadcoptère est présentée dans la figure ci-dessous, y compris les vitesses angulaires correspondantes, les couples et les forces créées par les rotors.
 |
 |
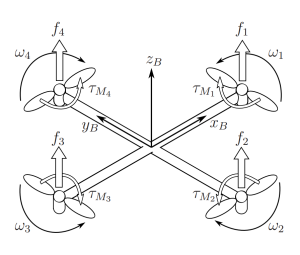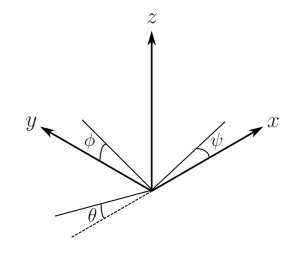
Figure 8-16 : Les cadres d’inertie et de carrosserie d’un quadricoptère
La position linéaire absolue [latex]ξ[/latex] du quadcoptère est définie dans le cadre de référence inertielle. La position angulaire est définie avec trois angles d’Euler [latex]η[/latex]. Le vecteur [latex]q[/latex] contient les vecteurs de position linéaire et angulaire.
| [latex]\begin{equation} \xi=\begin{bmatrix}x\\ y\\z \end{bmatrix}, \eta =\begin{bmatrix} \varnothing \\ \theta \\ \psi\end{bmatrix}, q= \begin{bmatrix} \xi \\ \eta \end{bmatrix} \end{equation}[/latex] | (8.8) |
L’origine du référentiel du corps se trouve au centre de masse du quadricoptère. Dans le référentiel du corps, les vitesses linéaires sont déterminées par [latex]V_{B}[/latex] et les vitesses angulaires par ν
| [latex]\begin{equation} V_B=\begin{bmatrix}v_{x}, B \\ v_{y}, B\\v_{z}, B \end{bmatrix}, v =\begin{bmatrix} p \\ q \\ r \end{bmatrix} \end{equation}[/latex] | (8.9) |
La matrice de rotation du référentiel du corps au référentiel inertiel est
| [latex]\begin{equation} R=\begin{bmatrix} C_{\psi }C_{\theta }C_{\psi }S_{\theta}S_{\phi } &- S_{\psi }C_{\theta }C_{\psi }S_{\theta}C_{\phi } &+ S_{\psi }S_{\theta }S_{\psi }C_{\theta}C_{\psi }S_{\theta}S_{\phi } &+ C_{\psi }C_{\theta }S_{\psi }S_{\theta}C_{\phi }-C_{\psi }S_{\theta } &-S_{\theta }C_{\theta}S_{\phi }C_{\theta}C_{\psi }\end{bmatrix} \end{equation}[/latex] | (8.10) |
Où [latex]S_{x}=\sin \left( x\right)[/latex]et [latex]C_{x}=\cos \left( S\right)[/latex].
La matrice de rotation R est orthogonale, [latex]R^{-1}=R^{T}[/latex]qui signifie qu’elle représente la rotation de référentiel inertiel au référentiel du corps. La matrice de transformation des vitesses angulaires du référentiel inertiel au référentiel du corps est [latex]W_{\eta}[/latex], et du référentiel du corps au référentiel inertiel est [latex]W_{\eta}^{-1}[/latex] :
| [latex]\begin{equation} \dot{\eta} =W_{\eta}^{-1}v \end{equation}[/latex] alors [latex]\begin{equation} v =W_{\eta}\dot{\eta} \end{equation}[/latex] | (8.11) |
Le quadricoptère est supposé avoir une structure symétrique avec les quatre bras alignés avec les axes x et y du corps. Ainsi, la matrice d’inertie est une matrice diagonale [latex]I[/latex] dans laquelle [latex]\begin{equation}I_{xx}= I_{yy}\end{equation}[/latex]
| [latex]\begin{equation} I=\begin{bmatrix} I_{xx} & 0 &0\\ 0& I_{yy} &0& \\0&0&I_{zz}\end{bmatrix} \end{equation}[/latex] | (8.12) |
L’inverse de l’équation suivante pourrait être utilisé pour résoudre les vitesses de rotor requises pour obtenir la poussée souhaitée [latex]T_{\Sigma}[/latex] et des instants [latex]\tau =\left( \tau _{1},\tau _{2},\tau _{3}\right)[/latex] du quadricoptère (Mahony, Kumar, & Corke, 2012);
| [latex]\begin{equation} \begin{pmatrix} T_{\Sigma} \\ \tau _{1} \\ \tau _{2} \\ \tau _{3} \end{pmatrix} = \begin{bmatrix} C_T & C_T & C_T & C_T \\ 0 & dc_T & 0 & -dc_T \\ -dc_T & 0 & dc_T & 0 \\ -C_q & C_q & -C_q & C_q \end{bmatrix} \begin{pmatrix} \omega _{1}^{2} \\ \omega _{2}^{2} \\ \omega _{3}^{2} \\ \omega _{4}^{2} \end{pmatrix}\end{equation}[/latex] | (8.13) |
Où [latex]C_T(>0)[/latex]et [latex]C_q[/latex]sont deux coefficients qui peuvent être déterminés expérimentalement pour le quadricoptère considéré à l’aide de tests de poussée.
8.3.3.3 Voilure fixe
Les UAV à voilure fixe nécessitent une piste pour le décollage et l’atterrissage, contrairement aux multirotors qui peuvent maintenir des vols stationnaires et des vitesses de vol plus faibles Cependant, les UAV à voilure fixe ont une endurance plus longue et peuvent voler à des vitesses de croisière plus élevées en raison de leur conception réussie basée sur les avions à voilure fixe plus grands avec quelques modifications et améliorations légères.
La voilure fixe est un élément principal qui génère la portance en réponse à l’accélération de l’avion vers l’avant. La vitesse et l’angle plus raide de l’air circulant sur la voilure fixe contrôlent la portance produite. Les drones à voilure fixe nécessitent une vitesse initiale plus élevée et un rapport poussée/charge inférieur à 1 pour initier un vol. Si l’on compare les drones à voilure fixe et les multirotors pour une charge utile identique, les drones à voilure fixe sont plus efficaces, car ils nécessitent moins de puissance et une charge de poussée inférieure à 1. L’orientation du UAV dans les angles de lacet, de roulis et de tangage est contrôlée par le gouvernail, les ailerons et les angles d’inclinaison longitudinale.
8.3.3.4 Autres robots volants
Il existe également des configurations non conventionnelles de UAV utilisés pour la recherche scientifique. Ils comprennent les drones hybrides, convertibles et à ailes battantes qui sont capables de décoller verticalement ou de se comporter comme des insectes pour des missions de reconnaissance. Les drones à ailes battantes, qui sont inspirés des insectes tels que les libellules [2] et les oiseaux [3], sont souvent mentionnés dans la littérature de recherche et parfois présentés sous forme de prototypes commerciaux. Grâce à leurs ailes légères et flexibles, ces drones peuvent assurer un vol stable même dans des conditions venteuses. Les drones à ailes battantes ont suscité beaucoup d’intérêt chez les chercheurs et les biologistes en raison de leurs avantages uniques en termes de maniabilité, ce qui a conduit à de nombreuses études sur le sujet. Les dirigeables et les ballons dirigeables sont d’autres types de robots volants qui utilisent un gaz de levage moins dense que l’air ambiant pour se maintenir en vol.
8.4 Contrôler les robots
En utilisant le modèle « Détecter-Penser-Agir », le contrôleur du robot peut être considéré comme le composant de l’élément Penser responsable des mouvements du robot. En général, un microcontrôleur, un ordinateur embarqué ou une combinaison des deux est utilisé pour stocker des informations sur le robot et son environnement, ainsi que pour exécuter les programmes conçus pour faire fonctionner le robot. Le Système de contrôle comprend le traitement des données, les algorithmes de contrôle, l’analyse logique et d’autres activités de traitement qui permettent au robot de fonctionner comme prévu. Les robots les plus sophistiqués sont dotés de systèmes de contrôle plus avancés pour répondre à des exigences spécifiques.
Le système de contrôle intègre les trois aspects de la boucle « Détecter-Penser-Agir » pendant l’exécution. Tout d’abord, le système de détection fournit des informations sur l’environnement, le robot lui-même et la relation entre le robot et l’environnement. Ensuite, sur la base des informations fournies par les capteurs et des objectifs du robot, le système de cognition (Penser) et de contrôle (Agir) doit décider de l’action à prendre pour atteindre les objectifs du robot. Enfin, les commandes appropriées sont envoyées aux actionneurs qui actionnent la structure mécanique. Le système de contrôle coordonne toutes les données d’entrée et planifie le mouvement du robot vers l’objectif souhaité.
Diverses techniques de contrôle ont été proposées et font l’objet de recherches. Les stratégies de contrôle des robots mobiles peuvent être classées en deux catégories : les stratégies de rétroaction en boucle ouverte et en boucle fermée. Lorsqu’il s’agit de contrôle en boucle ouverte, les opérateurs humains sont impliqués dans les décisions. Le robot transmet les informations à l’opérateur uniquement pour exécuter ses instructions. Un exemple d’un tel système est le pilotage d’un drone à l’aide d’un contrôleur de drone. Le succès du robot dans l’accomplissement de sa mission dépend essentiellement des compétences de pilotage de l’opérateur – le contrôleur transmet simplement l’intention de l’opérateur au drone. La plupart du temps, les commandes de contrôle telles que les vitesses ou les couples sont calculées au préalable, en fonction de la connaissance de la position initiale et finale (« Goal pose ») du robot. Cependant, cette stratégie ne peut pas compenser les perturbations et les erreurs de modèle (« Erreur »).
En outre, les stratégies de contrôle boucle fermée pourraient fournir la compensation nécessaire, car les entrées dépendent de l’état réel du système et non seulement des points initiaux et finaux. Ainsi, les perturbations et les erreurs qui causent des écarts par rapport à l’état prédit sont corrigées à l’aide de données de capteur en temps réel (« rétroaction »). (Figure 8-17). Formellement, on pourrait définir un contrôleur de rétroaction permettant à un robot d’atteindre et de maintenir l’état souhaité (appelé un point de consigne) en comparant à plusieurs reprises son état actuel avec l’état d’objectif souhaité. Ici, la rétroaction fait référence aux informations qui sont littéralement « réinjectées » dans le contrôleur du système. Lorsqu’un système fonctionne à l’état souhaité, on dit qu’il fonctionne en régime permanent.
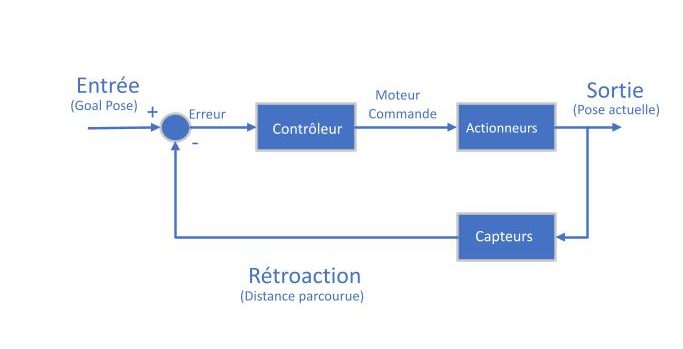Figure 8-17 : Un contrôleur de rétroaction en boucle fermée typique.
8.4.1 Régulateurs PID (proportionnel, intégral et dérivé)
Un régulateur PID est un mécanisme de rétroaction de boucle de contrôle qui calcule la différence entre une valeur souhaitée (point de consigne) et la sortie réelle d’un processus et utilise ce résultat pour appliquer une correction au processus. Le terme PID signifie un contrôle de rétroaction Proportionnel-Intégral-Dérivé, et c’est l’un des contrôleurs les plus couramment utilisés dans l’industrie. C’est un point de départ idéal pour la conception d’un système de contrôle autonome, et il est très couramment utilisé dans les systèmes de pilotage automatique commerciaux ainsi que dans les projets open source.
L’objectif principal de ce processus est de maintenir une valeur de consigne spécifique. Par exemple, on peut vouloir qu’un moteur à courant continu maintienne une valeur de consigne r(t) de 600 impulsions d’encodeur par seconde. La vitesse réelle du moteur y(t), qui est appelée la variable de processus, est soustraite de la valeur du point de consigne de 600 pour obtenir la valeur de l’erreur e(t). Le régulateur PID calcule ensuite la nouvelle valeur de contrôle u(t) à appliquer au moteur sur la base de la valeur d’erreur calculée. Dans le cas d’un moteur à courant continu, la valeur de contrôle serait un signal à modulation de largeur d’impulsion(). Le (t) représente un paramètre de temps passé dans le processus (Figure 8-18).
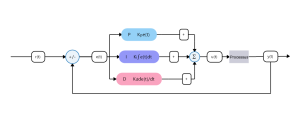
Figure 8-18 : Un régulateur PID implique que r(t) représente le point de consigne de référence, e(t) représente la différence entre la sortie du processus et le point de consigne souhaité, u(t) est la valeur de contrôle d’entrée du processus et y(t) est la sortie du processus.
Maintenant, examinons comment chacun des trois éléments, à savoir P, I et D, contribue au contrôleur global.
8.4.1.1 Contrôle proportionnel (P)
Cet élément prend une certaine proportion de la valeur d’erreur actuelle. La proportion est spécifiée par une constante appelée valeur de gain, et une réponse proportionnelle est représentée par les lettres Kp. Par exemple, la valeur Kp peut être réglée sur 0,25, ce qui calculera une valeur de 25 % de la valeur d’erreur. Ceci est utilisé pour calculer la réponse corrective au processus. Puisqu’il faut une erreur pour générer la réponse proportionnelle, il n’y a pas de partie proportionnelle de la réponse corrective s’il n’y a pas d’erreur. Par exemple, lors du contrôle autonome d’un drone, l’augmentation de la valeur du gain proportionnel, Kp conduit généralement à un temps de montée plus court (c’est-à-dire que le drone atteint rapidement l’altitude requise) et à des dépassements plus importants. Bien qu’il puisse diminuer le temps de stabilisation du système, il peut également conduire le drone à afficher un comportement très oscillatoire ou instable (Figure 8-19).
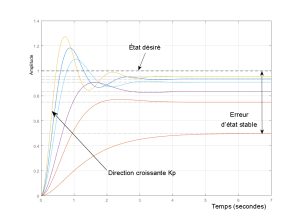
Figure 8-19 : Un exemple montrant les effets de l’augmentation de la valeur Kp – temps de montée plus court, mais augmentation du comportement oscillatoire. (Aucun contrôle intégral ni dérivé)
8.4.1.2 Contrôle dérivé (D)
Le terme dérivé est employé afin de prédire les tendances à venir de l’erreur en se basant sur son taux de variation actuel. Il est utilisé afin d’ajouter un effet d’amortissement au système, de sorte que plus le taux de changement est rapide, plus l’effet de contrôle ou d’amortissement est important. Par conséquent, augmenter le gain Kd du contrôle dérivé entraîne généralement une diminution du dépassement et un comportement mieux amorti. Toutefois, l’augmentation du gain Kd pourrait également entraîner des erreurs plus importantes en régime permanent. (Figure 8-20)
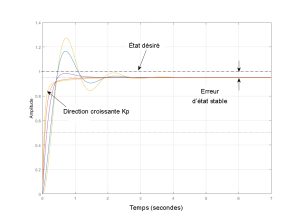
Figure 8-20 : Un exemple illustrant les effets de l’augmentation de Kd avec un Kp constant (aucun contrôle intégral)
8.4.1.3 Contrôle intégral (I)
L’élément I intègre toutes les valeurs d’erreur passées au fil du temps. Le terme « intègre » signifie simplement accumuler ou additionner. Il en résulte que le terme intégral augmente jusqu’à ce que l’erreur atteigne zéro. Une fois que l’erreur est corrigée, le terme intégral cesse d’augmenter. Si une erreur persiste même après l’application du contrôle proportionnel, le terme intégral tente de corriger l’erreur en ajoutant sa valeur accumulée d’erreur. Cela se traduira par une diminution de l’effet proportionnel à mesure que l’erreur diminue, et l’effet intégral croissant compense cela. L’augmentation du gain intégral, Ki entraîne une réduction de l’erreur en régime permanent (souvent élimination), mais peut également entraîner des oscillations plus importantes (Figure 8-21).
Un autre problème à prendre en compte lors de l’utilisation du terme intégral dans un contrôleur fait référence au windup intégral. Dans la plupart des systèmes physiques (systèmes non linéaires), il est courant de constater que des changements significatifs du point de consigne (en positif ou en négatif) entraînent l’accumulation d’erreurs importantes par le terme intégral. Ces erreurs ne peuvent pas être compensées par des erreurs dans la direction opposée, ce qui peut conduire à une perte de contrôle. Au fil des années, les chercheurs ont mis au point plusieurs techniques anti-windup pour contrer ce phénomène. Une technique courante consiste à définir des limites pour le terme intégral en fonction des limitations connues du système, telles que la plage de fonctionnement de l’actionneur.
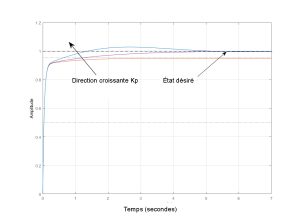
Figure 8-21 : Un exemple illustrant les effets de l’augmentation de la valeur Ki avec des valeurs constantes Kp et Kd.
8.4.1.4 Réglage d’un régulateur PID
Comme on peut le comprendre à partir de cet aperçu du rôle de chaque élément du régulateur PID, il n’est pas possible de régler de manière indépendante les trois gains différents. Chacun d’eux vise à offrir la caractéristique de réponse souhaitée (par exemple, une réponse plus rapide, des oscillations amorties et douces, une erreur de régime permanent proche de zéro), mais a un effet négatif qui doit être compensé en ajustant de nouveau un autre gain. En conséquence, le réglage du PID est une procédure hautement couplée et itérative. Le régulateur PID est constitué de l’action additive des composants proportionnel, intégral et dérivé. Tous ne sont pas nécessaires, c’est pourquoi nous utilisons souvent des régulateurs P, des régulateurs PI ou des régulateurs PD, lorsque le résultat souhaité peut être obtenu avec un régulateur plus simple.
8.4.2 Régulateurs à logique floue
La théorie de la logique floue a vu le jour dans les années 1960 afin de pallier l’imprécision et l’incertitude inhérentes aux systèmes de perception. Depuis lors, elle a trouvé de nombreuses applications en ingénierie. Pour de nombreux problèmes de contrôle non linéaires, notamment ceux liés à la navigation et à la robotique, elle est considérée comme l’une des solutions les plus simples disponibles. En effet, contrairement aux solutions traditionnelles, la logique floue permet aux ordinateurs de se comporter davantage comme des êtres humains, en traitant efficacement des entrées complexes et en gérant des notions linguistiques telles que « trop chaud », « trop froid » ou « parfait ». Par ailleurs, elle est bien adaptée aux implémentations à faible coût basées sur des capteurs peu onéreux, des convertisseurs analogique-numérique à faible résolution et des microcontrôleurs à 4 ou 8 bits. Il est facile d’améliorer les performances de ces systèmes en ajoutant de nouvelles règles ou fonctionnalités. Dans de nombreux cas, le contrôle flou peut être utilisé pour améliorer les systèmes de contrôle traditionnels en ajoutant une couche supplémentaire d’intelligence à la méthode de contrôle existante.
8.4.2.1 Un exemple simple
Considérez un robot terrestre se déplaçant vers une cible.
Le contrôleur à logique floue (CLF) utilisé possède deux entrées : erreur de distance ([latex]\Delta e_{d}[/latex]) et erreur d’angle d’orientation ([latex]\Delta e_{a}[/latex]) du robot. La sortie du contrôleur (c’est-à-dire les signaux de commande) serait des signaux de type modulation en largeur d’impulsion pour contrôler la vitesse angulaire des deux servomoteurs des roues. Par conséquent, le contrôleur à logique floue est un système à deux entrées et deux sorties. Le schéma fonctionnel du système robotique est présenté dans la Figure 8-22.
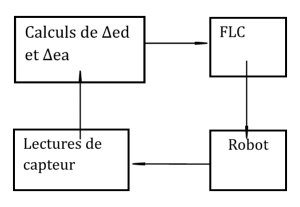
Figure 8-22 : Système de commande à logique floue
8.5 Planification de trajectoire
La planification de trajectoire consiste à trouver une trajectoire appropriée (optimale) pour que la plate-forme mobile se déplace de son point de départ au point d’arrivée dans un environnement donné. Les premiers travaux sur la planification de trajectoires se concentraient sur les manipulateurs robotiques, où un modèle mondial parfait et une connaissance précise des angles des articulations étaient supposés. Toutefois, ces hypothèses ne peuvent être faites pour des robots mobiles évoluant dans des environnements partiellement ou totalement inconnus avec des incertitudes de localisation.
Les algorithmes classiques, tels que l’algorithme de Dijkstra (Dijkstra, 1959), les algorithmes A et A* (Hart et al., 1968), appliquent une recherche globale de graphe pour trouver le chemin le moins coûteux du point de départ au point d’arrivée. D’autres méthodes utilisent l’échantillonnage de l’environnement local pour déterminer le chemin le moins coûteux (Kuffner et LaValle, 2000). L’objectif principal de l’obtention du meilleur chemin est de trouver le chemin le plus court avec une consommation d’énergie minimale et une couverture maximale d’une zone ou une qualité de perception prédite optimisée. Dans certaines situations, il est avantageux de choisir parmi un ensemble donné de trajectoires pouvant être suivies par le contrôleur du robot plutôt que de planifier un chemin spécifique et peut-être impossible (Dey et al., 2011). Par conséquent, différents algorithmes de planification de chemin sont utilisés en fonction des situations, la plupart reposant sur des techniques heuristiques et probabilistes.
8.5.1 Algorithmes heuristiques de planification de chemin
Les méthodes heuristiques utilisent une fonction du coût estimé pour la recherche de chemin orientée vers la cible, ce qui réduit considérablement le temps de calcul. Ces algorithmes calculent le chemin sur la base du plus petit nombre de cellules de grille dans la file d’attente, en attribuant un à chaque nœud en fonction de sa distance par rapport à la distance minimale entre les nœuds de départ et d’arrivée.
8.5.1.1 Algorithme A*
L’algorithme de planification de chemin le plus connu est (Hart et al., 1968), qui utilise une méthode de recherche du meilleur premier pour trouver le chemin le moins coûteux du nœud de départ au nœud de destination. Contrairement aux autres techniques de planification de chemin, on peut considérer que l’algorithme A* possède un « cerveau » qui peut faire les calculs. Il est largement utilisé dans les jeux et les cartes Web pour trouver le chemin le plus court de manière très efficace. Le véhicule se déplace jusqu’au nœud cible en utilisant une fonction heuristique pour évaluer la qualité de chaque nœud ou détermine s’il n’y a pas de chemin disponible.
L’algorithme A* fonctionne sur une carte graphique avec plusieurs nœuds. À chaque étape, il sélectionne le nœud en fonction de la valeur « f », qui est égale à la somme de « g » et « h ». À chaque étape, il choisit le nœud ayant la valeur « f » la plus basse et passe au suivant jusqu’à ce qu’il trouve le point d’arrivée.
| [latex]f(node)= g(node) +h(node)[/latex] | (8.14) |
Où : g(node) est le coût du déplacement du point initial au point actuel; h(node) est la fonction heuristique qui inclut le coût du nœud de départ à l’emplacement actuel, c(n, n′ ) et le coût estimé de l’emplacement actuel à l’objectif h(n′ ).
A* (étoile) Pseudocode de recherche de chemin
//Initialiser à la fois la liste ouverte et la liste fermée
laisse openList et closedList égales à une liste vide de nœuds
//Ajouter la nœud de départ
mettre startNode sur openList (laisser f à zéro)
//Effectuer la boucle jusqu’à trouver la fin
tant que openList n’est pas vide
//Récupérer le nœud actuel
laisser le currentNode égal au nœud avec la plus petite valeur f
supprimer le currentNode de openList
ajouter le currentNode à closedList
//A trouvé l’objectif
si currentNode est l’objectif
objectif trouvé! Revenir en arrière pour obtenir le chemin
//Générer les enfants
laisser les enfants de currentNode égaler les nœuds adjacents
pour chaque enfant dans l’enfant
//L’enfant est dans closedList
si l’enfant est dans closedList
continuer jusqu’au début de la boucle
//Créer les valeurs f, g et h
child.g = currentNode.g + distance entre enfant et courante
child.h = distance à partir de l’enfant jusqu’à la fin
child.f = child.g + child.h
// L’enfant est déjà dans openList
si child.position est dans les positions des nœuds de openList
si child.g est supérieur au nœud openList g continuez jusqu’au début de la boucle
// Ajouter l’enfant à openList
ajouter l’enfant à openList
Par exemple :
Nous aimerions trouver le chemin le plus court entre A et K dans la carte suivante. Le chiffre en rouge représente la distance entre les nœuds, et le chiffre en noir dans le cercle bleu représente la valeur heuristique. A* utilise f (n)=g (n) h(n) pour trouver le chemin le plus court.
Commençons par le point de départ A. A a trois nœuds : B, E et F, alors nous pouvons commencer à calculer f (B), f (E) et f (F) :
f (B) = 3 + 8 = 11
f (E) = 1 + 1 = 2
f ( F) = 5 + 4 = 9
f (E) < f (F) < f (B), nous choisirons donc E comme nouveau nœud de départ.
Pour le nœud E, il y a deux nœuds F et H, f (F) = 7 (1 6) 4 =11, f (H)= 3 (1 2) 4 = 7, f (H) < f (F), donc nous choisirons H comme nouveau nœud de départ.
Pour le nœud H, il a deux nœuds J et I, f (J) = 5 (1 2 2) 3 =8, f (I)= 4 (1 2 1) 2 = 6, f (I) < f (J ), nous choisirons donc I comme nouveau nœud de départ.
Pour le nœud I, il a deux nœuds D et K, f (D) = 10 (1 2 1 6) 5 =15, f (K)= 6(1 2 1 2) 0 = 6, f (K) < f (D), nous allons donc choisir K comme le nœud suivant, car K est le point d’arrivée, l’algorithme s’arrête ici.
Le chemin le plus court de A à K est A – E – H – I –K
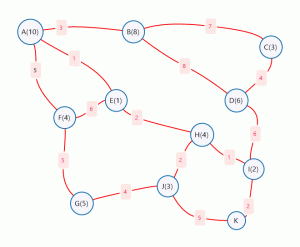
Figure 8-23 : Exemple d’algorithme A*.
L’algorithme A* est similaire à l’Algorithme de Dijkstra (Dijkstra, 1959), sauf qu’il oriente sa recherche vers les états les plus prometteurs, ce qui peut économiser une quantité importante d’effort de calcul. La limitation des approches mentionnées précédemment réside dans le fait qu’elles exigent une carte complète de la zone explorée. Toutefois, lorsqu’on travaille dans des scénarios réels, de nouvelles informations peuvent être ajoutées à la carte, ce qui rend la replanification essentielle. Alors qu’un algorithme A∗ pourrait être utilisé pour planifier à partir de zéro pour chaque mise à jour, cela coûte cher en termes de calculs.
Les algorithmes D* Lite (Koenig et Likhachev, 2005) et Focused Dynamic A* (D*) (Stentz et al., 1995), quant à eux, ne cherchent pas le chemin du début à la fin. Ils recherchent plutôt un chemin de la destination vers le début et mettent à jour les nœuds uniquement lorsque des changements surviennent. Un chemin mis à jour est calculé sur la base du chemin précédent, ce qui est beaucoup plus efficace que le l’algorithme A∗ et l’algorithme de Dijkstra. L’Algorithme D* Lite est l’un des algorithmes de navigation par objectif les plus populaires, largement utilisé pour la navigation de robots mobiles dans des environnements inconnus. Il s’agit d’une méthode de recherche inversée qui peut replanifier à partir de la position actuelle lorsque de nouveaux obstacles bloquent le chemin.
Enfin, Champ D* est un algorithme de planification et de replanification de chemin basé sur l’interpolation (Ferguson et Stentz, 2006). Contrairement à d’autres méthodes où les nœuds sont définis comme les centres des grilles, il définit les nœuds sur les coins des grilles. Ensuite, l’interpolation linéaire est utilisée pour créer des points de cheminement le long des bords des grilles, permettant la planification de trajets directs, peu coûteux et lisses dans des environnements non uniformes. Les variantes de l’algorithme D* sont largement utilisées pour les robots autonomes, notamment les rovers martiens et les voitures autonomes (Stentz et Hebert, 1995; Urmson et al., 2008).
8.5.2 Algorithmes probabilistes de planification de chemin
Les approches probabilistes de planification de chemin échantillonnent l’espace de configuration de manière aléatoire, ce qui permet de réduire le temps de planification du chemin et l’utilisation de la mémoire. Cependant, leur principal inconvénient est qu’ils ne peuvent pas toujours garantir de trouver le chemin optimal.
De nombreux travaux ont été menés sur la base de méthodes probabilistes de planification de chemin. L’une des approches les plus populaires est la carte routière probabiliste (Kavraki et Latombe, 1998; Kavraki et al., 1996). Cette approche se compose généralement de deux phases : premièrement, elle échantillonne aléatoirement des points dans l’espace de configuration pour construire un graphe de la carte routière, puis relie les configurations échantillonnées à leurs voisines; et deuxièmement, dans la phase de requête, les nœuds de départ et d’arrivée sont connectés à leurs voisins dans le graphe et le chemin est calculé à l’aide d’une méthode heuristique. Bien que la recherche d’un chemin existant soit possible avec un nombre suffisamment élevé d’échantillons, des stratégies d’échantillonnage délibérées sont nécessaires pour des situations telles que des couloirs étroits dans de grands environnements, car cela peut augmenter considérablement le temps de planification du chemin. Dans de nombreux cas, un prétraitement est nécessaire pour définir les obstacles avant d’exécuter plusieurs requêtes sur le même graphe basé sur les cartes routières probabilistes.
8.6 Évitement d’obstacle
En mobile robotique, l’objectif de l’évitement d’obstacle est généralement de naviguer d’un point de départ à un point de destination tout en évitant des collisions avec des obstacles pendant le mouvement du robot dans un environnement connu ou inconnu. Par conséquent, l’évitement d’obstacles est presque toujours combiné avec la planification de la trajectoire. Le processus d’évitement d’obstacles nécessite une connaissance de l’environnement, telle qu’une carte complète ou partielle, la position de l’objectif et la localisation du robot (discuté dans le chapitre suivant), ainsi que l’utilisation de capteurs tels que des caméras ou des capteurs laser pour détecter les obstacles.
L’évitement d’obstacles comprend toujours la détection d’obstacles et l’évitement de collision. Différents algorithmes utilisent divers types de capteurs et de techniques pour atteindre l’objectif de détection d’obstacles. Les données traitées reçues des capteurs sont ensuite envoyées au contrôleur pour diriger le robot afin d’éviter les obstacles. Il existe des algorithmes largement utilisés pour l’évitement d’obstacles, tels que les algorithmes de bogue, le VFH et d’autres techniques basées sur la proximité, tels que les capteurs sonar ou les capteurs de pare-chocs.
8.6.1. Algorithme Bug
Parmi toutes les techniques d’évitement d’obstacles, les méthodes d’évitement d’obstacles les plus simples sont les algorithmes Bug. L’algorithme Bug consiste à suivre le contour des obstacles sur le chemin du robot et à le contourner (Lumelsky et Stepanov, 1987; Lumelsky, 2005). Plusieurs variantes de l’algorithme Bug ont été développées, notamment l’algorithme Bug 1, Bug 2, DistBug et Tangential Bug.
L’algorithme Bug 1 est la plus simple parmi toutes les variantes de l’algorithme Bug. Il atteint presque toujours le point de destination avec une grande fiabilité Cependant, son efficacité est un sujet de préoccupation. Le robot suit le chemin le plus court entre sa position actuelle et le point de destination cible jusqu’à ce qu’il rencontre un obstacle sur son chemin. Lorsqu’il rencontre un obstacle, il commence à tourner autour de sa surface et calcule la distance depuis le point de destination. Après un tour complet, il détermine le point de départ le plus proche de la destination. Ensuite, il maintient ou modifie la direction de mouvement en fonction de la distance entre ce point et le point d’impact. Cette méthode peut être illustrée dans les étapes suivantes :
- Se dirige vers le point de destination
- Si un obstacle est rencontré, contournez-le et rappelez-vous à quelle distance vous vous rapprochez du point de destination
- Revenez au point le plus proche et continuez
Le robot contourne chaque obstacle sur son chemin vers la destination, ce qui peut augmenter la charge de calcul. Malgré cela, sa simplicité justifie son utilisation lorsque la tâche doit être effectuée indépendamment du temps nécessaire.
En général, les algorithmes Bug sont efficaces pour éviter un seul obstacle. Cependant, leurs fiabilités diminuent dans un environnement plus complexe et encombré, et selon les conditions particulières, certaines versions peuvent fonctionner mieux que d’autres.
8.6.2 L’histogramme de champ vectoriel (VFH)
L’histogramme de champ vectoriel est une méthode de navigation évitant les obstacles en temps réel pour les robots mobiles, développée par Borenstein et Koren (Borenstein, Koren, 1991). Cette méthode est composée de trois éléments principaux qui aident à éviter les obstacles. Tout d’abord, le robot génère un histogramme sensoriel bidimensionnel autour de son corps ou dans un angle limité et commence à mettre à jour les données de l’histogramme à chaque étape. Deuxièmement, les données de l’histogramme bidimensionnel sont converties en un histogramme polaire unidimensionnel. Enfin, il sélectionne la zone dense polaire inférieure et se déplace en calculant la direction.
Cette méthode permet de surmonter le problème de bruit des capteurs. Un histogramme est un graphique qui montre les probabilités de présence d’obstacles à l’angle associé à la lecture du capteur. Les probabilités sont obtenues en créant une carte quadrillée d’occupation locale (voir chapitre 9) de l’environnement du robot. L’histogramme permet de découvrir tous les passages suffisamment larges pour permettre le passage du robot. La sélection de la trajectoire est basée sur une fonction de coût qui prend en compte l’alignement de la trajectoire du robot avec l’objectif et la différence entre l’orientation actuelle des roues et la nouvelle direction. Une fonction de coût minimum est souhaitable. L’un des avantages de l’utilisation du VFH est qu’il résout le problème de bruit des capteurs en créant un histogramme polaire qui représente la probabilité d’obstacle dans une direction angulaire particulière. Certains inconvénients doivent être pris en considération lors de l’utilisation de cette technique, comme VFH ne garantit pas l’exhaustivité, ce qui peut conduire à une tâche inachevée. Il peut s’avérer problématique de traverser un passage étroit en utilisant cette méthode. De plus, il ne tient pas compte de la dynamique du robot et de son environnement, ce qui le rend peu adapté à une utilisation dans un environnement dynamique complexe.
8.7 Résumé du chapitre
Les robots qui se déplacent dans leur environnement plutôt que de rester fixes à un endroit sont appelés robots mobiles. Ces robots peuvent être classés en fonction de leur type de locomotion, comme les robots à roues, à pattes ou volants.
Le contrôleur de robot fournit essentiellement les commandes de contrôle à ses actionneurs pour diriger le robot vers l’objectif souhaité. Une boucle de contrôle courante est le régulateur PID (proportionnel-intégral-dérivé), qui utilise la rétroaction des capteurs pour mettre à jour le signal de contrôle de manière répétée. En substance, le régulateur applique une correction à une fonction de contrôle où la correction peut être proportionnelle à l’erreur (P), refléter l’erreur cumulée (I) ou le changement de taux d’erreur (D). Un régulateur PID nécessite un réglage de ses paramètres, ce qui nécessite généralement une approche itérative par essais et erreurs ou des algorithmes de réglage sophistiqués pour obtenir des performances optimales.
Afin qu’un robot se déplace d’un point initial à un point objectif donné, il doit élaborer un itinéraire entre les deux points en utilisant des critères optimaux tels que la distance la plus courte, la consommation d’énergie la plus faible ou la plus grande zone de couverture. Au fil des années, de nombreuses techniques ont été développées, y compris des techniques heuristiques et probabilistes, chacune ayant ses avantages et inconvénients. De plus, un problème connexe en matière de planification de trajectoire est le problème d’évitement d’obstacles. Encore une fois, les chercheurs ont élaboré diverses stratégies et techniques pour résoudre ce problème.
En tant que concepteur de robots mobiles, votre responsabilité est de choisir, élaborer et appliquer des techniques, algorithmes et plates-formes basées sur les concepts discutés dans ce chapitre, afin de satisfaire les exigences de la tâche à accomplir.
8.8 Questions de révision
- Si vous utilisez un régulateur PID pour un drone, l’augmentation du gain P Kp conduit-elle généralement à des temps de montée plus courts ou plus longs?
- Si vous utilisez un régulateur PID pour un drone, l’augmentation du gain I de KI entraînerait-elle des oscillations plus petites ou plus grandes?
- En comparant les robots à deux roues, trois roues et quatre roues, lequel d’entre eux est le plus instable?
- Que signifient le tangage, le lacet et le roulis dans un drone?
- Quelle est la différence entre les algorithmes de planification de chemin classiques et heuristiques ?
8.9 Lectures supplémentaires
Le chapitre couvrait des éléments d’introduction sur plusieurs sujets connexes. Une fois les concepts de base bien compris, vous pouvez explorer ces sujets plus en profondeur et développer des sujets avancés. Les titres suivants, offrent des excellentes lectures Introduction à la robotique : Mécanique et contrôle (3e édition) par Jean Craig, Mécanique, planification et contrôle de la robotique moderne par Kevin M. Lynch et Modélisation, planification et contrôle robotiques par Bruno Siciliano. Un autre livre fortement recommandé sur les robots mobiles est le livre de Roland Siegwart, Introduction aux robots mobiles autonomes.
https://en.wikibooks.org/wiki/Robotics/Types_of_Robots/Wheeled, 2021
da Silva, Lucian R., Rodolfo CC Flesch, and Julio E. Normey-Rico. « Analysis of anti-windup techniques in PID control of processes with measurement noise. » IFAC-PapersOnLine 51.4 (2018): 948-953. http://dx.doi.org/10.1016/j.ifacol.2018.06.100
RÉFÉRENCES
Dijkstra, E. W. (1959). A note on two problems in connexion with graphs. Numerische mathematik, 1(1), 269–271. https://doi.org/10.1007/BF01386390
Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. Systems Science and Cybernetics, IEEE Transactions on, 4(2), 100–107. https://doi.org/10.1109/TSSC.1968.300136
Kuffner, J. J. and LaValle, S. M. (2000). Rrt-connect: An efficient approach to single-query path planning. In Robotics and Automation, 2000. Proceedings. ICRA’00. IEEE International Conference on, volume 2, pages 995–1001. IEEE. http://dx.doi.org/10.1109/ROBOT.2000.844730
Dey, D., Liu, T. Y., Sofman, B., and Bagnell, D. (2011). Efficient optimisation of control libraries. Technical report, DTIC Document. https://doi.org/10.1609/aaai.v26i1.8383
Koenig, S. and Likhachev, M. (2005). Fast replanning for navigation in unknown terrain. Robotics, IEEE Transactions on, 21(3), 354–363. https://doi.org/10.1109/TRO.2004.838026
Stentz, A. et al. (1995). The focussed D* algorithm for real-time replanning. In IJCAI, volume 95, pages 1652–1659. https://robotics.caltech.edu/~jwb/courses/ME132/handouts/Dstar_ijcai95.pdf
Stentz, A. and Hebert, M. (1995). A complete navigation system for goal acquisition in unknown environments. Autonomous Robots, 2(2), 127–145. https://doi.org/10.1007/BF00735431
Urmson, C., Anhalt, J., Bagnell, D., Baker, C., Bittner, R., Clark, M., Dolan, J., Duggins, D., Galatali, T., Geyer, C., et al. (2008). Autonomous driving in urban environments: Boss and the urban challenge. Journal of Field Robotics, 25(8), 425–466. https://doi.org/10.1007/978-3-642-03991-1_1
Ferguson, D. and Stentz, A. (2006). Using interpolation to improve path planning: The field D* algorithm. Journal of Field Robotics, 23(2), 79–101. http://dx.doi.org/10.1002/rob.20109
Kavraki, L. E. and Latombe, J.-C. (1998). Probabilistic roadmaps for robot path planning. https://doi.org/10.1109/70.660866
Kavraki, L. E., Svestka, P., Latombe, J.-C., and Overmars, M. H. (1996). Probabilistic roadmaps for path planning in high-dimensional configuration spaces. Robotics and Automation, IEEE Transactions on, 12(4), 566–580. https://doi.org/10.1109/70.508439
Lumelsky, V. J., and Stepanov, A. A. (1987). Path-planning strategies for a point mobile automaton moving amidst unknown obstacles of arbitrary shape. Algorithmica 2, 403–430 https://doi.org/10.1007/BF01840369
Lumelsky, V. J. (2005). Sensing, Intelligence, Motion: How Robots and Humans Move in an Unstructured World. New York, NY: John Wiley & Sons. http://dx.doi.org/10.1002/0471738204.fmatter
Mahony, R., Kumar, V., & Corke, P. (2012). Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor. IEEE Robotics & Automation Magazine, 19(3), 20-32. doi:10.1109/MRA.2012.2206474 https://doi.org/10.1109/MRA.2012.2206474
Borenstein, J.; Koren, Y. (1991). « The vector field histogram-fast obstacle avoidance for mobile robots ». IEEE Transactions on Robotics and Automation. 7 (3): 278–288. https://doi.org/10.1109/70.88137
D Zhao, X Jing, W Dan, et al. Gait Definition and successive gait-transition method based on energy consumption for a quadruped. Chinese Journal of Mechanical Engineering, 2012, 25(1): 29–37. https://doi.org/10.3901/CJME.2012.01.029
Y Fukuoka, H Kimura. Dynamic locomotion of a biomorphic quadruped ‘Tekken’ robot using various gaits: walk, trot, free-gait and bound. Applied Bionics & Biomechanics, 2009, 6(1): 63–71. https://doi.org/10.1080/11762320902734208
Ed, Darack, 2014. https://www.airspacemag.com/flight-today/build-your-own-drone-180951417
Liste des figures
Figure 8-3 : Géométrie du véhicule d’un robot à trois roues typique
Figure 8-4 : Modèle de robot simplifié
Figure 8-5 : Configuration des roues d’un robot à deux roues
Figure 8-6 : Entraînement Ackerman
Figure 8-7 : Un ensemble de roues Mecanum (un type de roue Omni) sur un robot domestique
Figure 8-11 : Un robot hexapode (Crédit Bryce Cronin)
Figure 8-12 : Roulis, tangage et lacet
Figure 8-15 : Une configuration de rotor de quadricoptère
Figure 8-16 : Les cadres d’inertie et de carrosserie d’un quadricoptère
Figure 8-17 : Un contrôleur de rétroaction en boucle fermée typique
Figure 8-22 : Système de commande à logique floue
Figure 8-23 : Exemple d’algorithme A*
