6 Blocs de construction mathématiques : De la géométrie aux quaternions aux bayésiens
Rebecca Stower, Bruno Belzile, and David St-Onge
Table des matières
6.3 Géométrie de base et algèbre linéaire
6.3.2 Représentation vectorielle/matrice
6.3.3 Opérations vectorielles/matrices de base
6.4 Transformations géométriques
6.4.4 Matrices de transformation homogènes
6.7.2 Population générale et échantillons
6.7.4 Le modèle linéaire général
6.1 Objectifs d’apprentissage
L’objectif à la fin de ce chapitre est de maîtriser les compétences suivantes :
- utiliser des opérations vectorielles et matricielles;
- représenter la translation, la mise à l’échelle et la symétrie dans les opérations matricielles;
- comprendre l’utilisation et les limites des angles et des quaternions d’Euler;
- utiliser des transformations homogènes;
- utiliser des dérivées pour trouver les optimums d’une fonction et linéariser une fonction;
- comprendre l’importance et la définition d’une distribution gaussienne;
- utiliser des tests t et des ANOVA pour valider les hypothèses statistiques
6.2 Introduction
De nombreux domaines de la robotique reposent sur des principes de physique et de statistiques. Bien que ce livre s’efforce d’aborder chaque sujet de manière accessible, la plupart des chapitres supposent une connaissance de base en mathématiques. Les pages suivantes résument une variété étendue de concepts mathématiques, allant de la géométrie aux statistiques. Tout au long de ce chapitre, des exemples de fonctions Python pertinentes seront inclus.
6.3 Géométrie de base et algèbre linéaire
Cette section propose un aperçu succinct, mais non exhaustif, des concepts fondamentaux de la géométrie euclidienne. De plus, elle rappelle certaines opérations d’algèbre linéaire qui sont utiles pour manipuler des éléments dans différentes matrices ou tableaux.
6.3.1 Systèmes de coordonnées
Un système de coordonnées est défini comme un « système permettant de spécifier des points en utilisant des coordonnées mesurées de manière spécifique » [1]. Le plus courant, que vous avez très probablement utilisé dans le passé, est le système de coordonnées cartésien, comme illustré à la Figure 6-1. Dans le cas spécifique de l’espace tridimensionnel (3D), il existe un point d’origine à partir duquel les coordonnées sont mesurées, ainsi que trois axes indépendants et orthogonaux, X, Y et Z. Il est nécessaire d’avoir trois axes qui soient indépendants, mais ils ne sont pas obligés d’être orthogonaux. Cependant, dans la plupart des applications (mais pas toutes), il est préférable d’utiliser des axes orthogonaux pour des raisons pratiques (Hassenpflug, 1995).
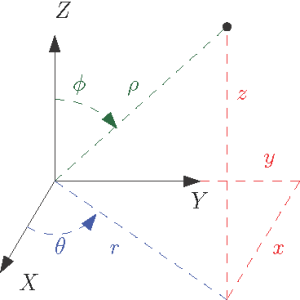
Figure 6-1 : Différents systèmes de coordonnées dans l’espace 3D
Il existe des alternatives courantes aux coordonnées cartésiennes qui peuvent être plus appropriées pour certaines applications, comme les coordonnées sphériques et cylindriques.
Dans le premier cas, les coordonnées sont définies par une distance ρ à partir de de l’origine et de deux angles, c’est-à-dire θ et ϕ. Dans ce dernier, qui est une extension des coordonnées polaires en 2D, une distance radiale r, un azimut (angle) θ et une coordonnée axiale (hauteur) z sont nécessaires. Alors qu’un point est défini uniquement avec des coordonnées cartésiennes, ce n’est pas totalement le cas avec des coordonnées sphériques et cylindriques; plus précisément, l’origine est définie par un ensemble infini de coordonnées avec ces deux systèmes, car les angles ne sont pas définis à l’origine. De plus, vous pouvez additionner/soustraire des multiples de 360° à chaque angle et vous vous retrouverez avec le même point, mais des coordonnées différentes. De plus, il est important d’être attentif aux conventions utilisées pour les coordonnées sphériques et cylindriques, car les variables utilisées pour définir les coordonnées individuelles peuvent être inversées selon le contexte et la discipline. Les conventions peuvent différer entre les physiciens, les mathématiciens et les ingénieurs [2].
6.3.2 Représentation vectorielle/matrice
En mathématiques, un vecteur est défini « comme une quantité qui possède à la fois une magnitude et une direction, et est généralement représenté par un segment de droite orienté dont la longueur représente la magnitude et la direction dans l’espace représente la direction » [3]. Cependant, cette définition ne fait pas référence aux composants et aux systèmes de référence que nous rencontrons souvent lorsqu’il s’agit de vecteurs. Il existe en effet une confusion courante entre la quantité physique représentée par un vecteur et sa représentation de la même quantité dans un système de coordonnées à l’aide de tableaux unidimensionnels. Le même mot, vecteur, est utilisé pour désigner ces tableaux, mais vous devez faire attention à bien distinguer les deux. Généralement, une flèche sur une lettre minuscule définit un vecteur, la quantité physique, par exemple [latex]\overrightarrow{a}[/latex], et une lettre minuscule en gras représente un vecteur défini dans un repère, c’est-à-dire avec des composantes, par exemple a. Veuillez noter cependant que les auteurs utilisent parfois des conventions différentes. Dans ce livre, le système de coordonnées utilisé pour représenter un vecteur est indiqué par un exposant. Par exemple, la variable [latex]\mathbf{b}^{S}[/latex] représente l’incarnation de [latex]\overrightarrow{b}[/latex] dans le cadre S, alors que [latex]\mathbf{b}^{\cal T}[/latex] représente l’incarnation de [latex]\overrightarrow{b}[/latex] dans le cadre [latex]\cal T[/latex]. Ils n’ont pas les mêmes composants, mais ils demeurent le même vecteur.
Vecteurs [latex]\overrightarrow{a}[/latex] et [latex]\overrightarrow{b}[/latex] dans un espace euclidien à n dimensions peuvent être affichés avec leurs composants comme
| [latex]\mathbf{a} = \begin{bmatrix}a_1\\a_2\\a_3\\\vdots \\ a_{n-1}\\a_n\end{bmatrix},\quad \mathbf{b} = \begin{bmatrix}b_1\\b_2\\b_3\\\vdots \\ b_{n-1}\\b_n\end{bmatrix}[/latex] | (6.1) |
par exemple, les vecteurs [latex]\overrightarrow{c}[/latex] et [latex]\overrightarrow{d}[/latex] sont illustrés à la Figure 6-2. Comme on peut le voir, deux cadres de référence sont également affichés. Leurs composants dans ces cadres sont
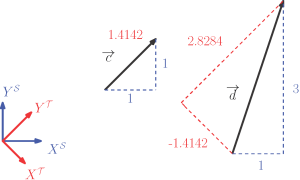
Figure 6-2 : Vecteurs planaires et leurs composants dans différents cadres
import numpy as np # Importation des bibliotheques
# tableaux
a = np.array([1,1]) # vecteur
A = np.array([1,2],
[3,4]) # matrice
De même, les tenseurs sont utilisés pour représenter les propriétés physiques d’un corps (et bien d’autres choses). De manière plus formelle, les tenseurs sont des objets algébriques qui définissent des relations multilinéaires entre différents objets dans un espace vectoriel. Cependant, ne vous attardez pas trop sur la définition mathématique, mais plutôt sur ce que vous connaissez déjà. Vous avez déjà rencontré des tenseurs dans ce chapitre, car les scalaires et les vecteurs (la quantité physique, pas le tableau) sont respectivement des tenseurs de rang 0 et de rang 1 [4]. Par conséquent, les tenseurs peuvent être considérés comme une généralisation des scalaires et des vecteurs. Un exemple de tenseur de rang 2 est le tenseur d’inertie d’un corps rigide, qui représente la distribution de masse à l’intérieur du corps rigide (indépendamment du référentiel utilisé). Pour faciliter les calculs numériques, la représentation d’un tenseur de rang 2 dans un système de coordonnées peut être réalisée à l’aide d’une matrice. Cependant, il est important de ne pas confondre les matrices avec les tenseurs de rang 2. En effet, tous les tenseurs de rang 2 peuvent être représentés par une matrice, mais toutes les matrices ne sont pas des tenseurs de rang 2. En d’autres termes, les matrices ne sont que des boîtes (tableaux) avec des nombres à l’intérieur (composants) qui peuvent être utilisées pour représenter différents objets, parmi lesquels des tenseurs de rang 2. Les matrices sont généralement représentées par des lettres majuscules en gras, par ex. [latex]\mathbf{A}[/latex]. Les matrices, qui ont des composants, peuvent également être définies dans des référentiels spécifiques. Par conséquent, l’exposant pour désigner le cadre de référence s’applique également aux matrices du livre, par exemple, [latex]\mathbf{H}^{\cal S}[/latex] représente une matrice de transformation homogène (on le verra dans la section 6.4.4) défini dans S.
D’autres matrices courantes avec des caractéristiques typiques comprennent :
- la matrice carrée, qui est une matrice avec un nombre égal de lignes et de colonnes;
- la matrice diagonale, qui n’a que des composantes non nulles sur sa diagonale, c’est-à-dire des composantes [latex](1, 1), (2, 2), . . . , (n, n)[/latex];
- la matrice d’identité [latex]\mathbf{1}[/latex], qui représente une [latex](n\times n)[/latex] matrice avec seulement 1 sur la diagonale, les autres composantes étant toutes égales à 0.
6.3.3 Opérations vectorielles/matrices de base
Les vecteurs et les matrices sont des outils mathématiques puissants et polyvalents qui possèdent de nombreuses propriétés et opérations. Nous rappellerons les plus utiles en robotique dans ce qui suit.
Produit interne
L’addition et la multiplication à l’aide d’opérations scalaires avec des vecteurs sont tout simplement réparties sur les composants. Sinon, les deux opérations les plus pertinentes en robotique sont les produits scalaires et vectoriels dot productscalar productcross product. Le produit interne est également connu sous le nom de produit scalaire, car le résultat du produit interne de deux vecteurs arbitraires est un scalaire. Laisser [latex]\overrightarrow{a}[/latex]et [latex]\overrightarrow{b}[/latex] être deux vecteurs arbitraires et leur amplitude correspondante [5] être [latex]\| \overrightarrow{a} \|[/latex] et [latex]\| \overrightarrow{b} \|[/latex], alors le produit interne de ces deux vecteurs est
| [latex]\begin{equation}\overrightarrow{a}\cdot\overrightarrow{b}=\| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos\theta\end{equation}[/latex] | (6.3) |
où θ représente l’angle entre ces deux vecteurs. Si les deux vecteurs sont orthogonaux, par définition, le résultat sera nul. Si des composants sont utilisés, alors nous avons
| [latex]\begin{equation}\mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+a_3b_3+\dots+a_{n-1}b_{n-1}+a_nb_n\end{equation}[/latex] | (6.4) |
import numpy as np # Importation des bibliotheques
# produit interne
np.dot(a,b) # produit interne de deux entrees de type tableau
np.linalg.multi dot(a,b,c) # produit interne de deux tableaux ou plus en un seul appel
# magnitude un vecteur
np.linalg.norm(a)
En utilisant les valeurs numériques précédemment données dans (6.2), le produit interne de [latex]\overrightarrow{a}[/latex]et [latex]\overrightarrow{b}[/latex] est :
| [latex]\begin{align}\overrightarrow{a}\cdot\overrightarrow{b}=1.4142\cdot3.1623 \cos(0.4636)=&4 \end{align}[/latex] | (6.5) |
| [latex]\begin{align}\mathbf{a}^{\cal S}\cdot\mathbf{b}^{\cal S}=1\cdot1+1\cdot3=&4 \end{align}[/latex] | (6.6) |
| [latex]\begin{align}\mathbf{a}^{\cal T}\cdot\mathbf{b}^{\cal T}=0\cdot1.4142+1.4142\cdot2.8284=&4 \end{align}[/latex] | (6.7) |
Comme vous pouvez le voir sur cet exemple, les définitions géométriques et algébriques du produit interne sont équivalentes.
Produit vectoriel
L’autre type de multiplication avec des vecteurs est le produit vectoriel.
Contrairement au produit interne, le produit vectoriel de deux vecteurs donne un autre vecteur, pas un scalaire. Encore une fois, les deux vecteurs doivent avoir la même dimension.
Avec [latex]\overrightarrow{a}[/latex] et [latex]\overrightarrow{b}[/latex] utilisés ci-dessus, le produit vectoriel est défini comme
| [latex]\begin{equation} \overrightarrow{a}\times\overrightarrow{b}=\| \overrightarrow{a} \| \| \overrightarrow{b} \| \sin\theta\overrightarrow{e} \end{equation}[/latex] | (6.8) |
où, comme pour le produit interne, θ représente l’angle entre [latex]\overrightarrow{a}[/latex]et [latex]\overrightarrow{b}[/latex] , et [latex]\overrightarrow{e}[/latex] représente un vecteur unitaire [6] orthogonal aux deux premiers . Sa direction est établie avec la règle de la main droite. Dans l’espace 3D, les composants du vecteur résultant peuvent être calculés avec la formule suivante :
| [latex]\begin{equation} \mathbf{a}\times\mathbf{b}=\begin{bmatrix} a_2b_3-a_3b_2\\ a_3b_1-a_1b_3\\ a_1b_2-a_2b_1 \end{bmatrix} \end{equation}[/latex] | (6.9) |
où [latex]\mathbf{a}=[a_1\quad a_2\quad a_3]^T[/latex] et [latex]\mathbf{b}=[b_1\quad b_2\quad b_3]^T[/latex]
La règle de la main droite right-hand rule permet de déterminer facilement la direction d’un vecteur résultant du produit vectoriel de deux autres. Tout d’abord, vous pointez dans la direction du premier vecteur avec vos doigts restants, puis courbez-les pour pointer dans la direction du deuxième vecteur. Selon cette règle, le pouce de la main droite pointera dans la direction du vecteur résultant, qui est normal au plan formé par les deux vecteurs initiaux.
import numpy as np # Importation des bibliotheques
# produit vectoriel
np.cross(a,b)
Encore une fois, en utilisant les valeurs numériques utilisées ci-dessus dans (6.2), nous pouvons calculer le produit vectoriel. Bien entendu, puisque ces deux vecteurs sont plans et que le produit vectoriel est défini sur l’espace 3D, la troisième composante de Z est supposée être égale à zéro. Voici le résultat :
| [latex]\begin{align} \overrightarrow{a}\times\overrightarrow{b}=1.4142\cdot3.1623 \sin(0.4636)\overrightarrow{k}=&2\overrightarrow{k}\end{align}[/latex] | (6.10) |
| [latex]\mathbf{a}^{\cal S}\times\mathbf{b}^{\cal S}=\begin{bmatrix} 1\cdot0-0\cdot3\\ 0\cdot1-1\cdot0\\ 1\cdot3-1\cdot1 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 2 \end{bmatrix}[/latex] | (6.11) |
| [latex]\begin{align}\mathbf{a}^{\cal T}\times\mathbf{b}^{\cal T}=\begin{bmatrix} 1.4142\cdot0-0\cdot2.8284\\ 0\cdot-1.41421356-1.4142\cdot0\\ 0\cdot2.8284-1.4142\cdot-1.4142 \end{bmatrix}=&\begin{bmatrix} 0\\ 0\\ 2 \end{bmatrix}\end{align}[/latex] | (6.12) |
où [latex]\overrightarrow{k}[/latex] est le vecteur unitaire parallèle à l’axe Z. Par cette définition, vous pouvez observer que le vecteur unitaire définissant l’axe Z d’un référentiel cartésien est simplement le produit vectoriel des vecteurs unitaires définissant le X et les axes Y , suivant l’ordre donné par la règle de la main droite. Ces trois vecteurs unitaires sont communément étiquetés [latex]\overrightarrow{i}[/latex] , [latex]\overrightarrow{j}[/latex] et [latex]\overrightarrow{k}[/latex], comme illustré à la Figure 6-3. Vous devez noter que le produit vectoriel du vecteur unitaire [latex]\overrightarrow{a}[/latex] avec [latex]\overrightarrow{j}[/latex] se traduit également par [latex]\overrightarrow{k}[/latex] , depuis [latex]\overrightarrow{a}[/latex] est aussi dans le plan XY . De plus, comme vous pouvez le constater avec le produit vectoriel de [latex]\overrightarrow{i}[/latex] et [latex]\overrightarrow{k}[/latex] illustré sur la même figure, un vecteur n’est pas attaché à un point particulier de l’espace. Comme mentionné précédemment, il est défini par une direction et une magnitude, ainsi l’endroit où il est représenté n’a aucun impact sur le résultat du produit vectoriel.
Multiplication matricielle
Comme pour les vecteurs, l’addition et la multiplication par un scalaire sont également réparties sur les composants des matrices. Par contre, la multiplication matricielle est un
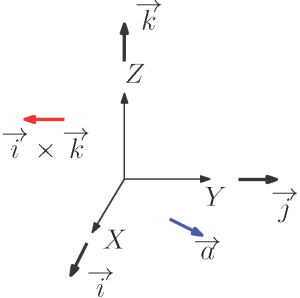
Figure 6-3 : Vecteurs unitaires définissant un repère cartésien
peu plus compliquée. Définissons la matrice A par des vecteurs lignes et la matrice B par des vecteurs colonnes, c’est-à-dire :
| [latex]\begin{equation} \mathbf{A}=\begin{bmatrix}\mathbf{a}_1\\\mathbf{a}_2\\\mathbf{a}_3\\\vdots\\\mathbf{a}_{n-1}\\\mathbf{a}_n\end{bmatrix},\quad \mathbf{B}=\begin{bmatrix}\mathbf{b}_1&\mathbf{b}_2&\mathbf{b}_3&\dots&\mathbf{b}_{n-1}&\mathbf{b}_n\end{bmatrix} \end{equation}[/latex] | (6.13) |
Ensuite, la multiplication matricielle est définie comme :
| [latex]\begin{equation} \mathbf{A}\mathbf{B}=\begin{bmatrix} \mathbf{a}_1\cdot\mathbf{b}_1 & \mathbf{a}_1\cdot\mathbf{b}_2 & \mathbf{a}_1\cdot\mathbf{b}_3 & \dots & \mathbf{a}_1\cdot\mathbf{b}_{n-1} & \mathbf{a}_1\cdot\mathbf{b}_{n}\\ \mathbf{a}_2\cdot\mathbf{b}_1 & \mathbf{a}_2\cdot\mathbf{b}_2 & \mathbf{a}_2\cdot\mathbf{b}_3 & \dots & \mathbf{a}_2\cdot\mathbf{b}_{n-1} & \mathbf{a}_2\cdot\mathbf{b}_{n}\\ \mathbf{a}_3\cdot\mathbf{b}_1 & \mathbf{a}_3\cdot\mathbf{b}_2 & \mathbf{a}_3\cdot\mathbf{b}_3 & \dots & \mathbf{a}_3\cdot\mathbf{b}_{n-1} & \mathbf{a}_3\cdot\mathbf{b}_{n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ \mathbf{a}_{n-1}\cdot\mathbf{b}_1 & \mathbf{a}_{n-1}\cdot\mathbf{b}_2 & \mathbf{a}_{n-1}\cdot\mathbf{b}_3 & \dots & \mathbf{a}_{n-1}\cdot\mathbf{b}_{n-1} & \mathbf{a}_{n-1}\cdot\mathbf{b}_{n}\\ \mathbf{a}_n\cdot\mathbf{b}_1 & \mathbf{a}_n\cdot\mathbf{b}_2 & \mathbf{a}_n\cdot\mathbf{b}_3 & \dots & \mathbf{a}_n\cdot\mathbf{b}_{n-1} & \mathbf{a}_n\cdot\mathbf{b}_{n}\\ \end{bmatrix} \end{equation}[/latex] | (6.14) |
Bien que ce résultat puisse sembler effrayant au premier abord, vous pouvez voir que le [latex](i,j)[/latex] composant [7] est simplement le produit interne de [latex]i^{è}[/latex] rangée de la première matrice et la [latex]j^{è}[/latex] colonne de la deuxième matrice. Le nombre de colonnes de la première matrice [latex]\mathbf{A}[/latex] doit être égal au nombre de lignes de la deuxième matrice [latex]\mathbf{B}[/latex].
import numpy as np # Importation des bibliotheques
# multiplication matricielle
np.matmul(A,B) # pour les tableaux de type entrees
A @ B # pour les entrees ndarray
Pour illustrer cette opération, définissons [latex]\mathbf{A}[/latex] et [latex]\mathbf{B}[/latex] représentant [latex](2\times2)[/latex] des matrices, c’est-à-dire :
| [latex]\begin{equation} \mathbf{A}=\begin{bmatrix} 1 & 2\\3 & 4 \end{bmatrix},\quad \mathbf{B}=\begin{bmatrix} 1 & 0\\-1 & 2 \end{bmatrix} \end{equation}[/latex] | (6.15) |
Alors, le résultat de la multiplication matricielle est :
| [latex]\begin{equation} \mathbf{A}\mathbf{B}=\begin{bmatrix} 1\cdot1-2\cdot1 & 1\cdot0+2\cdot2\\3\cdot1-4\cdot1 & 3\cdot0+4\cdot2 \end{bmatrix}= \begin{bmatrix} -1 & 4\\-1 & 8 \end{bmatrix} \end{equation}[/latex] | (6.16) |
Il est essentiel que vous compreniez que la multiplication matricielle est non commutative, ce qui signifie que l’ordre compte, comme vous pouvez le constater dans l’exemple suivant avec des matrices [latex]\mathbf{A}[/latex] et [latex]\mathbf{B}[/latex] utilisées ci-dessus :
| [latex]\begin{equation} \mathbf{A}\mathbf{B}= \begin{bmatrix} -1 & 4\\-1 & 8 \end{bmatrix},\textrm{ but}\quad \mathbf{B}\mathbf{A}= \begin{bmatrix} 1 & 2\\5 & 6 \end{bmatrix} \end{equation}[/latex] | (6.17) |
Transposition d’une matrice
Une autre opération courante sur une matrice est le calcul de sa transposée, à savoir une opération qui retourne une matrice sur sa diagonale. La matrice générée, notée [latex]\mathbf{A}^T[/latex] a les indices de ligne et de colonne commutés par rapport à [latex]\mathbf{A}[/latex]. Par exemple, avec un [latex](3\times3)[/latex] matrice [latex]\mathbf{C}[/latex], sa transposée est définie comme :
| [latex]\begin{equation} \mathbf{C}^T=\begin{bmatrix} c_{1,1} & c_{1,2} & c_{1,3}\\ c_{2,1} & c_{2,2} & c_{2,3}\\ c_{3,1} & c_{3,2} & c_{3,3} \end{bmatrix}^T =\begin{bmatrix} c_{1,1} & c_{2,1} & c_{3,1}\\ c_{1,2} & c_{2,2} & c_{3,2}\\ c_{1,3} & c_{3,2} & c_{3,3} \end{bmatrix} \end{equation}[/latex] | (6.18) |
import numpy as np # Importation des bibliotheques
# transposition de matrice
np.transpose(A) # fonction pour une entree de type tableau
A.transpose() # methode pour ndarray
A.T # attribut pour ndarray
Puisque les vecteurs (tableau de composants) sont fondamentalement des matrices [latex](1\times n)[/latex], la transposition peut être utilisée pour calculer le produit interne de deux vecteurs avec une multiplication matricielle, c’est-à-dire
| [latex]\begin{equation} \mathbf{a}\cdot\mathbf{b}=\mathbf{a}^T\mathbf{b}=a_1b_1+a_2b_2+\dots+a_nb_n \end{equation}[/latex] | (6.19) |
Déterminant et inverse d’une matrice
Enfin, il convient de faire une brève introduction à l’inverse d’une matrice, qui est une notion courante en robotique, couvrant des domaines tels que la mécanique, le contrôle et l’optimisation. Laisser [latex]\mathbf{A}[/latex] représenter une [latex](n\times n)[/latex] matrice carrée [8]; cette matrice est inversible si
| [latex]\begin{equation} \mathbf{A}\mathbf{B}=\mathbf{1},\quad \textrm{et}\quad \mathbf{B}\mathbf{A}=\mathbf{1} \end{equation}[/latex] | (6.20) |
Ensuite, la matrice [latex]\mathbf{B}[/latex] est l’inverse de [latex]\mathbf{A}[/latex], et peut donc s’écrire [latex]\mathbf{A}^{-1}[/latex]. Les composants de [latex]\mathbf{A}^{-1}[/latex] peuvent être calculés formellement avec la formule suivante :
| [latex]\begin{equation} \mathbf{A}^{-1}=\frac{1}{\textrm{det}(\mathbf{A})}\mathbf{C}^T \end{equation}[/latex] | (6.21) |
où [latex]\textrm{det}(\mathbf{A})[/latex] s’appelle le déterminant de [latex]\mathbf{A}[/latex] et [latex]\mathbf{C}[/latex] représente la matrice des cofacteurs [9] de [latex]\mathbf{A}[/latex].
Le déterminant d’une matrice, un scalaire parfois étiqueté [latex]|\mathbf{A}|[/latex], est égal à, dans le cas d’une matrice [latex](2\times2)[/latex],
| [latex]\begin{equation} \textrm{det}(\mathbf{A})= ad-bc, \quad \textrm{où}\quad \mathbf{A}=\begin{bmatrix} a & b\\c & d \end{bmatrix} \end{equation}[/latex] | (6.22) |
De même, pour une matrice [latex]3\times3[/latex], nous avons
| [latex]\begin{equation} \textrm{det}(\mathbf{A})= a(ei-fh)-b(di-fg)+c(dh-eg), \quad \textrm{où}\quad \mathbf{A}=\begin{bmatrix} a & b & c\\d & e & f\\g & h & i \end{bmatrix} \end{equation}[/latex] | (6.23) |
Le déterminant d’une matrice est critique pour le calcul de son inverse, car un déterminant de 0 correspond à une matrice singulière , qui n’a pas d’inverse. L’inverse d’une matrice [latex](2\times2)[/latex] peut être calculé formellement avec la formule suivante
| [latex]\begin{equation} \mathbf{A}^{-1}= \frac{1}{ad-bc}\begin{bmatrix} d & -b\\-c & a \end{bmatrix}, \quad \textrm{où}\quad \mathbf{A}=\begin{bmatrix} a & b\\c & d \end{bmatrix} \end{equation}[/latex] | (6.24) |
De même, pour une matrice [latex]3\times3[/latex], nous avons
| [latex]\begin{equation} \mathbf{A}^{-1}= \frac{1}{\textrm{det}(\mathbf{A})}\begin{bmatrix} (ei-fg) & -(bi-ch) & (bf-ce)\\ -(di-fg) & (ai-cg) & -(af-cd)\\ (dh-eg) & -(ah-bg) & (ae-bd) \end{bmatrix}, \quad \textrm{où}\quad \mathbf{A}=\begin{bmatrix} a & b & c\\d & e & f\\g & h & i \end{bmatrix}\label{e:inv3D} \end{equation}[/latex] | (6.25) |
import numpy as np # Importation des bibliotheques
# determinant de la matrice
np.linalg.det(A)
# matrice inverse
np.linalg.inv(A)
Comme vous pouvez le voir sur l’équation (6.25), vous ne pouvez pas inverser une matrice avec un déterminant égal à zéro, car cela entraînerait une division par zéro. L’inverse d’une matrice est un outil utile pour résoudre un système d’équations linéaires. En effet, un système de n équations avec n inconnues peut être exprimé sous forme de matrice comme
| [latex]\begin{equation} \mathbf{A}\mathbf{x}=\mathbf{b} \end{equation}[/latex] | (6.26) |
où les inconnues sont les composantes de [latex]\mathbf{x}[/latex], les constantes sont les composantes de [latex]\mathbf{b}[/latex] et les facteurs devant chaque inconnue sont les composantes de la matrice [latex]\mathbf{A}[/latex]. Par conséquent, nous pouvons trouver la solution de ce système, à savoir les valeurs des variables inconnues, comme
| [latex]\begin{equation} \mathbf{x}=\mathbf{A}^{-1}\mathbf{b} \end{equation}[/latex] | (6.27) |
Inverses généralisés
Cependant, si nous avons plus d’équations (m) que le nombre d’inconnues (n), le système est surdéterminé, et donc [latex]\mathbf{A}[/latex] n’est plus une matrice carrée. Ses dimensions sont [latex](m\times n)[/latex]. Une solution exacte à ce système d’équations ne peut généralement pas être trouvée. Dans ce cas, on utilise une inverse généralisée ; une stratégie pour trouver une solution optimale. Plusieurs inverses généralisés, ou pseudo-inverse, se trouvent dans la littérature (Ben-Israel and Greville, 2003), chacune avec un critère d’optimisation différent. Dans le contexte de ce livre, nous présentons ici uniquement un type spécifique, à savoir l’inverse généralisé de Moore-Penrose (MPGI). Dans le cas de systèmes surdéterminés, le MPGI est utilisé pour trouver une solution approximative qui minimise la norme euclidienne de l’erreur. Cette norme est définie comme
| [latex]\begin{equation} \mathbf{e}_0=\mathbf{b}-\mathbf{A}\mathbf{x}_0 \end{equation}[/latex] | (6.28) |
où [latex]\mathbf{x}_0[/latex] et [latex]\mathbf{e}_0[/latex] sont respectivement la solution approximative et l’erreur résiduelle. La solution approximative est calculée avec
| [latex]\begin{equation} \mathbf{x}_0=\mathbf{A}^L\mathbf{b},\quad \mathbf{A}^L=(\mathbf{A}^T\mathbf{A})^{-1}\mathbf{A}^T \end{equation}[/latex] | (6.29) |
où [latex]\mathbf{A}^L[/latex] est nommée l’inverse généralisé de Moore-Penrose de gauche (LMPGI), puisque [latex]\mathbf{A}^I\mathbf{A}=\mathbf{1}[/latex].En guise d’exercice, vous pouvez tenter de démontrer cette équation. Il existe un autre MPGI qui peut être utile en robotique, mais pas aussi commun que le LMPGI, le inverse généralisé de Moore-Penrose de droite (RMPGI). L’inverse généralisé de droite est défini comme
| [latex]\begin{equation} \mathbf{A}^R \equiv \mathbf{A}^T(\mathbf{A}\mathbf{A}^T)^{-1},\quad \mathbf{A} \mathbf{A}^R = \mathbf{1}\label{e:RMPGI} \end{equation}[/latex] | (6.30) |
où [latex]\mathbf{A}[/latex] est un une matrice [latex]m\times n[/latex] avec [latex]m < n[/latex], c’est-à-dire représentant un système d’équations linéaires avec plus d’inconnues que d’équations. Dans ce cas, ce système admet une infinité de solutions. Par conséquent, notre objectif n’est pas de trouver la meilleure solution approximative, mais plutôt une solution avec une norme minimale (euclidienne). Par exemple, en robotique, lorsqu’il existe un ensemble infini de configurations articulaires possibles pour atteindre une position arbitraire avec précision à l’aide d’un manipulateur, le MPGI à droite peut nous donner la configuration en minimisant les rotations articulaires. Avec les deux inverses généralisés présentés ici, nous supposons que [latex]\mathbf{A}[/latex] représente une matrice de plein rangmatrix!rank, ce qui signifie que ses colonnes individuelles sont indépendantes si [latex]m > n[/latex], ou ses lignes individuelles sont indépendantes si [latex]m < n[/latex]. Dans le cas d’une matrice carrée [latex](m = n)[/latex], une matrice de plein rang est tout simplement non singulière.
6.4 Transformations géométriques
En robotique, il est essentiel de pouvoir décrire les relations géométriques de manière claire et sans ambiguïté. Cela est réalisé à l’aide de systèmes de coordonnées et de cadres de référence, comme mentionné précédemment. Il est possible que vous ayez déjà étudié quatre types de transformations géométriques : la translation, la mise à l’échelle, la symétrie (miroir) et la rotation. Nous allons les passer rapidement en revue, car elles sont toutes utiles pour la conception assistée par ordinateur. Cependant, il est important de noter que les transformations utilisées pour mapper les coordonnées d’une image dans une autre ne font appel qu’à la translation et à la rotation.
Dans un souci de clarté, nous présenterons toutes les transformations géométriques sous forme de matrices, afin de bénéficier des opérations et des propriétés puissantes qu’elles offrent, ainsi que de leur format condensé. En utilisant l’introduction vectorielle ci-dessus (Section 6.3.2), l’élément géométrique le plus simple sera utilisé pour introduire la transformation, le point :
| [latex]\begin{equation} P_{2D}(x,y)=\begin{bmatrix}x\\ y\end{bmatrix},~ P_{3D}(x,y,z)=\begin{bmatrix}x\\ y\\ z\end{bmatrix} \end{equation}[/latex] | (6.31) |
En réalité, il est possible d’appliquer des transformations aux entités ponctuelles afin de transformer n’importe quelle géométrie en 2D ou en 3D. à partir d’un ensemble de points, il est possible de définir des paires connectées, telles que des arêtes ou des lignes, et à partir d’un ensemble de lignes, on peut définir des boucles, c’est-à-dire des surfaces. Enfin, un ensemble de surfaces sélectionnées peut définir un solide.
6.4.1 Transformations de base
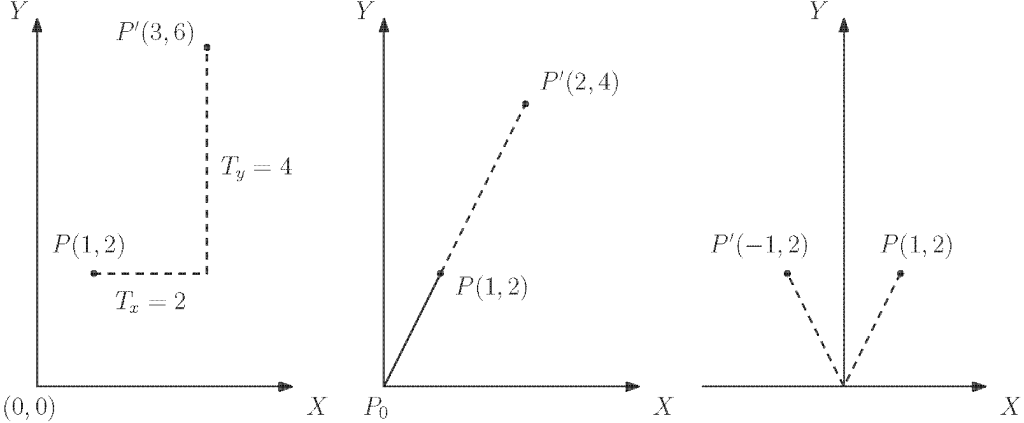
Figure 6-4 : Transformations géométriques de base, de gauche à droite : translation, mise à l’échelle et miroir (symétrie).
Commençons par un exemple numérique : étant donné un point dans [latex]x = 1[/latex] et [latex]y = 2[/latex] que nous avons l’intention de nous déplacer de 2 unités vers x positif et de 4 unités vers y positif.
La forme algébrique de cette opération est simplement [latex]x′ = x + 2[/latex]et [latex]y′ = y + 4[/latex], qui peut s’écrire sous forme matricielle :
| [latex]\begin{equation} P’=P+T=\begin{bmatrix}1\\ 2\end{bmatrix}+\begin{bmatrix}2\\ 4\end{bmatrix} \end{equation}[/latex] | (6.32) |
Un raisonnement similaire s’applique en trois dimensions. Imaginons maintenant que nous utilisons le point [latex]P[/latex] pour définir une ligne avec l’origine [latex]P_0=\begin{bmatrix}0\\ 0\end{bmatrix}[/latex]et que nous voulons étirer cette ligne avec un facteur d’échelle de 2. La forme algébrique de cette opération est simplement
| [latex]\begin{equation} P’=SP=\begin{bmatrix}2 & 0\\ 0 & 2\end{bmatrix}\begin{bmatrix}1\\ 2\end{bmatrix} \end{equation}[/latex] | (6.33) |
Cette opération de mise à l’échelle est appelée proportionnelle, puisque les deux axes ont le même facteur d’échelle. L’utilisation de différents facteurs d’échelle peut entraîner une déformation de la géométrie. Cependant, au lieu de simplement appliquer une mise à l’échelle à la géométrie, il est possible d’utiliser une matrice diagonale similaire pour changer le signe d’un ou plusieurs de ses composants. Cela aura pour effet de générer une symétrie. Par exemple, une symétrie par rapport à y est écrit:
| [latex]\begin{equation} P’=SP=\begin{bmatrix}-1 & 0\\ 0 & 1\end{bmatrix}\begin{bmatrix}1\\ 2\end{bmatrix} \end{equation}[/latex] | (6.34) |
Ces opérations sont simples et ne changent pas avec l’augmentation des dimensions de deux à trois. Les rotations, cependant, ne sont pas en tant que telles.
6.4.2 Rotations 2D/3D
Une rotation est une transformation géométrique qui s’introduit plus facilement avec des coordonnées polaires (voir la Figure 6-5):
| [latex]\begin{equation} P=\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}r\cos(\alpha)\\ r\sin(\alpha)\end{bmatrix} \end{equation}[/latex] | (6.35) |
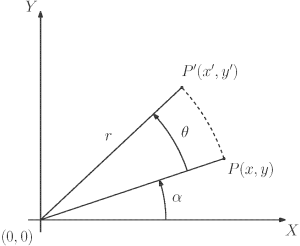
Figure 6-5 : Rotation planaire et coordonnées polaires.
Puis une rotation θ appliqué à ce vecteur consiste à :
| [latex]\begin{equation} P’=\begin{pmatrix}r\cos(\alpha+\theta)\\ r\sin(\alpha+\theta)\end{pmatrix}, \end{equation}[/latex] | (6.36) |
qui peut être divisé par rapport aux angles en utilisant des identités trigonométriques communes conduisant à P′ =
| [latex]\begin{equation} P’=\begin{bmatrix}x\cos(\theta)-y\sin(\theta)\\ x\sin(\theta)+y\cos(\theta)\end{bmatrix}=\begin{bmatrix}\cos(\theta) & -\sin(\theta)\\ \sin(\theta) & \cos(\theta)\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix} \label{e:2drot} \end{equation}[/latex] | (6.37) |
La matrice résultante [latex]2\times2[/latex] est appelée matrice de rotation et son format est unique en 2D.
Toute rotation dans le plan peut être représentée par cette matrice, en utilisant la règle de droite pour le signe de θ. Cette matrice est unique, car il existe un seul axe de rotation pour la géométrie plane : la perpendiculaire au plan (souvent définie comme z − axis). En ce qui concerne la géométrie dans l’espace tridimensionnel, il existe une infinité d’axes de rotation potentiels. Il suffit de visualiser les mouvements de rotation que l’on peut appliquer à un objet tenu dans la main. Une approche pour relever ce défi consiste à définir un vecteur directeur dans l’espace et un angle de rotation autour de celui-ci, puisque Leonhard Euler nous a appris que « dans l’espace tridimensionnel, tout déplacement d’un corps rigide tel qu’un point sur le corps rigide reste fixe, équivaut à une rotation unique autour d’un axe passant par le point fixe ». Bien que cette représentation soit intéressante pour les amateurs de géométrie, elle n’est pas pratique à implémenter dans des programmes informatiques pour des rotations généralisées. Au lieu de cela, nous pouvons décomposer toute rotation tridimensionnelle en une séquence de trois rotations autour des axes principaux. Cette approche est appelée Euler’s Angles et est la représentation la plus courante de la rotation tridimensionnelle. Il suffit de définir trois matrices :
| [latex]\mathbf{R}_x=\begin{bmatrix}1 & 0 & 0\\ 0 & \cos(\psi) & -\sin(\psi)\\ 0 & \sin(\psi) & \cos(\psi)\end{bmatrix},[/latex] | (6.38) |
| [latex]\mathbf{R}_y=\begin{bmatrix}\cos(\phi) & 0 & \sin(\phi)\\ 0 & 1 & 0\\-\sin(\phi) & 0 & \cos(\phi)\end{bmatrix},[/latex] | (6.39) |
| [latex]\mathbf{R}_z=\begin{bmatrix}\cos(\theta) & -\sin(\theta) & 0\\ \sin(\theta) & \cos(\theta) & 0\\ 0 & 0 & 1\end{bmatrix}[/latex] | (6.40) |
Bien que ces matrices soient suffisantes pour représenter toutes les rotations, elles laissent néanmoins deux définitions arbitraires en suspens :
- l’orientation des axes principaux [latex](x − y − z)[/latex] dans l’espace,
- l’ordre des rotations.
Les matrices de rotation sont des opérations de multiplication sur des caractéristiques géométriques, et comme cela a été mentionné précédemment, ces opérations ne sont pas commutatives. La solution consiste à s’entendre sur un ensemble universel de conventions :
| [latex]\begin{equation} XYX,~XYZ,~XZX,~XZY,~YXY,~YXZ,~YZX,~YZY,~ZXY,~ZXZ,~ZYX,~et~ZYZ \end{equation}[/latex] | (6.41) |
Ces douze conventions nécessitent encore la définition de l’orientation de leurs axes : chaque axe peut soit être fixé au repère inertiel (souvent appelé rotations extrinsèques) ou attaché au corps en rotation (souvent appelé rotations intrinsèques. Par exemple, la matrice de rotation fixe pour la convention XYZ est :
| [latex]\begin{equation} \mathbf{R}_z\mathbf{R}_y\mathbf{R}_x=\begin{bmatrix}\cos_{\theta}\cos_{\phi} & \cos_{\theta}\sin_{\phi}\sin_{\psi}-\sin_{\theta}\cos_{\psi} & \cos_{\theta}\sin_{\phi}\cos_{\psi}+\sin_{\theta}\sin_{\psi}\\ \sin_{\theta}\cos_{\phi} & \sin_{\theta}\sin_{\phi}\sin_{\psi}-\cos_{\theta}\cos_{\psi} & \sin_{\theta}\sin_{\phi}\cos_{\psi}-\cos_{\theta}\sin_{\psi}\\ -\sin_{\phi} & \cos_{\phi}\sin_{\psi} & \cos_{\phi}\cos_{\psi}\end{bmatrix} \end{equation}[/latex] | (6.42) |
Bien que l’utilisation d’un cadre de référence fixe puisse sembler plus facile à visualiser, la plupart des contrôleurs intégrés exigent que les mouvements de rotation soient exprimés dans le cadre du corps lui-même attaché à l’objet et se déplace avec lui. La même convention XY Z, mais dans le cadre mobile est :
| [latex]\begin{equation} \mathbf{R}_x'\mathbf{R}_y'\mathbf{R}_z'=\begin{bmatrix} \cos_{\phi}\cos_{\theta} & -\cos{\phi}\sin_{\theta} & \sin_{\phi}\\ \cos_{\psi}\sin_{\theta}+\sin_{\psi}\sin_{\phi}\cos_{\theta} & \cos_{\psi}\cos_{\theta}-\sin_{\psi}\sin_{\phi}\sin_{\theta} & -\sin_{\psi}\cos_{\phi}\\ \sin_{\psi}\sin_{\theta}-\cos_{\psi}\sin_{\phi}\cos_{\theta} & \sin_{\psi}\cos_{\theta}+\cos_{\psi}\sin_{\phi}\sin_{\theta} & \cos_{\psi}\cos_{\phi}\end{bmatrix} \end{equation}[/latex] | (6.43) |
En aviation, la convention la plus courante est le ZYX (roulis-tangage-lacet) aussi appelé la variante Tait-Bryan. En robotique, chaque fabricant et développeur de logiciels décide de la convention qu’il préfère utiliser. Par exemple, FANUC et KUKA utilisent la convention d’angle d’Euler XYZ fixe, tandis qu’ABB utilise la convention d’angle d’Euler mobile ZYX.
Pour ce qui est de la conception assistée par ordinateur, les angles d’Euler utilisés dans CATIA et SolidWorks sont décrits selon la convention des angles d’Euler mobiles ZYZ.
Il est important de noter qu’une limitation majeure de la représentation des angles d’Euler est le phénomène connu sous le nom de verrouillage du cardan.gimbal lock. En un coup d’oeil, chaque convention présente des orientations singulières, ce qui signifie qu’il existe des configurations où deux axes se superposent, ayant ainsi le même effet sur la rotation. Lorsque deux axes génèrent la même rotation, il y a des zones de l’espace tridimensionnel qui ne sont plus accessibles, c’est-à-dire qu’une rotation devient impossible. Le verrouillage du cardan est devenu un problème assez répandu dans le contrôle des engins spatiaux depuis qu’il a été observé lors de la mission Apollo (Jones and Fjeld, 2006). Néanmoins, les angles d’Euler demeurent la représentation la plus courante et la plus intuitive pour la rotation et l’orientation tridimensionnelles. Cependant, en raison de la limitation du verrouillage du cardan, d’autres représentations, souvent plus complexes, ont été introduites pour y remédier.
6.4.3 Quaternion
L’une de ces représentations sans verrouillage de cardan est le quaternion. Le quaternion est un concept mathématique assez complexe par rapport au niveau requis pour ce manuel.
Nous n’essayerons pas de définir précisément le quaternion en fonction de sa construction mathématique ni de détailler toutes ses propriétés et opérations. Cependant, vous pouvez appréhender le concept en le comparant aux nombres imaginaires, un concept mathématique plus courant.
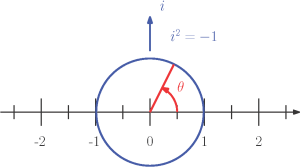
Figure 6-6 : Représentation vectorielle de la rotation plane à l’aide de l’axe imaginaire i.
On rappelle que l’axe imaginaire [latex](i)[/latex] est orthogonal aux nombres réels un (voir la Figure 6-6), avec la propriété unique [latex]i^2=-1[/latex]. Ensemble, ils créent un cadre de référence plan qui peut être utilisé pour exprimer des rotations :
| [latex]\begin{equation} R(\theta)=\cos(\theta)+\sin(\theta)i \label{e:im} \end{equation}[/latex] | (6.44) |
En d’autres termes, nous pouvons représenter une rotation dans le plan sous la forme d’un vecteur avec une partie imaginaire. Maintenant, imaginez que nous ajoutions deux rotations supplémentaires, comme défini précédemment avec les angles d’Euler. Pour représenter ces rotations, nous aurons besoin de deux autres axes orthogonaux « imaginaires ». L’équation (6.44) devient :
| [latex]\begin{equation} R(\theta)=\cos(\theta)+\sin(\theta)(\text{x}i+\text{y}j+\text{z}k) \end{equation}[/latex] | (6.45) |
Bien que cela puisse être facilement confondu avec une représentation d’angle vectoriel, il faut se rappeler que [latex]i−j −k[/latex] définit des axes « imaginaires »; et non pas des coordonnées dans l’espace cartésien. Ces axes ont des propriétés similaires à celles des axes plus courants [latex]i[/latex] axe imaginaire :
| [latex]\begin{equation} \left\| i,j,k\right\|=1,~ji=-k,~ij=k,~i^2=-1 \end{equation}[/latex] | (6.46) |
Pour la plupart des gens, il peut être difficile de visualiser les quaternions par rapport aux angles d’Euler. Cependant, les quaternions offrent une représentation sans singularité et présentent plusieurs avantages du point de vue informatique. C’est pourquoi les développeurs de ROS (voir chapitre 5) ont choisi les quaternions comme représentation standard. En Python la bibliothèque scipy contient un ensemble de fonctions permettant de passer facilement d’une représentation à une autre :
# Importer la bibliotheque
from scipy.spatial.transform import Rotation as R
# Creer une rotation avec des angles Euler
mat = R.from euler(’yxz’, [45, 0, 30], degrees=True)
print("Euler: ", mat.as euler(’yxz’, degrees=True))
# Imprimer le quaternion resultant
print("Quaternion: ", mat.as quat ())
6.4.4 Matrices de transformation homogènes
Une méthode normalisée pour appliquer une transformation d’un système de coordonnées à un autre, c’est-à-dire pour mapper un vecteur d’un référentiel à un autre, consiste à utiliser des matrices de transformation homogènes. En effet, une matrice de transformation homogène peut être utilisée pour décrire à la fois la position et l’orientation d’un objet. La [latex](4\times4)[/latex] matrice de transformation homogène est définie comme
| [latex]\begin{equation} \mathbf{H}_{\cal S}^{\cal T} \equiv \begin{bmatrix} \mathbf{Q} & \mathbf{p}\\ \mathbf{0}^T & 1 \end{bmatrix} \label{e:DH_transformation} \end{equation}[/latex] | (6.47) |
où Q est la [latex](3\times3)[/latex] matrice de rotation (orientation), [latex]\mathbf{p}[/latex] est le vecteur tridimensionnel définissant la position cartésienne[latex][x,\quad y,\quad z][/latex] de l’origine et [latex]\mathbf{0}[/latex] est le vecteur nul tridimensionnel. Comme on peut le constater avec l’exposant et l’indice de [latex]\mathbf{H}[/latex], la matrice définit le référentiel [latex]\cal T[/latex] dans le cadre du référentiel [latex]\cal S[/latex]. Effectivement, bien que les matrices de transformation homogènes soient composées de 9 composantes, elles ne sont pas toutes indépendantes, car la position et l’orientation dans l’espace cartésien totalisent 6 degrés de liberté (DoF). La matrice homogène combine la translation mentionnée précédemment avec la rotation, ce qui permet d’utiliser uniquement des multiplications pour effectuer la transformation, au lieu d’ajouter séparément la translation et la rotation.
6.5 Probabilité de base
6.5.1 Probabilité
Lorsque nous parlons de probabilité, nous sommes généralement intéressés par la prédiction de la probabilité qu’un événement se produise, exprimée en [latex]P(event)[/latex]. Au niveau le plus élémentaire, cela peut être conceptualisé comme une proportion représentant le nombre d’événements qui nous intéressent (qui satisfont certains critères spécifiques) divisé par le nombre total d’événements possibles, qui ont tous une probabilité égale.
Vous trouverez ci-dessous un résumé de la notation utilisée pour décrire les différents types et combinaisons d’événements de probabilité qui seront utilisés dans la suite de cette section.
| P(A) | Probabilité que A se produise |
| P(A′) | Probabilité que A ne se produise pas |
| P(A ∩ B) | Probabilité que A et B se produisent à la fois |
| P(A ∪ B) | Probabilité que A ou B se produise |
| P(A|B) | Probabilité que A se produise étant donné que B se produit |
Tableau 6-1 : Notations de probabilité courantes
Par exemple, supposons que nous ayons un dé à 6 faces typique (non truqué). Chacune des six faces a une probabilité égale de se produire à chaque lancer du dé. Par conséquent, le nombre total de résultats possibles lors d’un seul lancer de dé, chacun ayant une probabilité égale de se produire, est de 6. Ainsi, nous pouvons représenter la probabilité d’obtenir un nombre spécifique lors d’un lancer de dé comme une proportion sur 6.
Par exemple, la probabilité d’obtenir un 3 peut être exprimée par :
| [latex]\begin{equation} P(3) = \frac{1}{6} \end{equation}[/latex] | (6.48) |
La probabilité d’un événement qui ne se produit pas est toujours l’inverse de la probabilité qu’il se produise, ou [latex]1 - P(\textrm{event})[/latex]. Ceci est connu sous le nom de règle de soustraction.
| [latex]\begin{equation} P(A) = 1 - P(A') \end{equation}[/latex] | (6.49) |
Ainsi, dans l’exemple ci-dessus, la probabilité de ne pas obtenir un 3 est :
| [latex]\begin{equation} P(3') = 1 - \frac{1}{6} = \frac{5}{6} \end{equation}[/latex] | (6.50) |
On pourrait aussi modifier nos critères pour être plus généraux, par exemple en calculant la probabilité d’obtenir un nombre pair lors d’un lancer de dé. Dans ce cas, nous avons maintenant 3 résultats possibles qui satisfont nos critères (obtenir un 2, un 4 ou un 6), mais le nombre total d’événements possibles reste à 6. Ainsi, la probabilité d’obtenir un nombre pair est :
| [latex]\begin{equation} P(\textrm{even}) = \frac{3}{6} = \frac{1}{2} \end{equation}[/latex] | (6.51) |
Maintenant, imaginons que nous élargissions ces critères pour calculer la probabilité d’obtenir soit un nombre pair, soit un nombre supérieur à 3 lors d’un lancer de dé. Nous avons maintenant deux critères distincts qui nous intéressent (être un nombre pair ou être supérieur à 3), et nous voulons calculer la probabilité qu’un seul lancer de dé donne l’un ou l’autre de ces résultats.
Pour commencer, nous pourrions simplement essayer d’additionner la probabilité de chaque résultat individuel :
| [latex]\begin{equation} \begin{split} P(\textrm{even } \cup > 3) &= \frac{3}{6} + \frac{3}{6} = \frac{6}{6} = 1 \end{split} \end{equation}[/latex] | (6.52) |
En effet, nous nous sommes retrouvés avec une probabilité de 1, ce qui signifie une certitude de 100. L’erreur de calcul provient du fait qu’il existe des nombres qui sont à la fois pairs ET supérieurs à 3 (à savoir, 4 et 6). En additionnant simplement les probabilités, nous avons « compté deux fois » leur probabilité de se produire, ce qui a faussé le résultat. Dans la Figure 6-7, nous pouvons constater que si nous créons un diagramme de Venn avec des nombres pairs et des nombres > 3, ils se chevauchent au milieu avec les valeurs de 4 et 6. Si nous considérons la probabilité comme le calcul de la surface totale de ces cercles dans un diagramme de Venn, nous n’avons besoin de compter qu’une seule fois le chevauchement des événements.
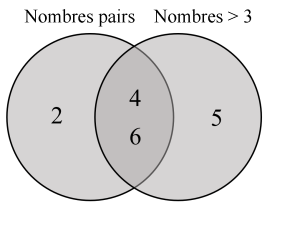
Figure 6-7 : Diagramme de Venn des nombres pairs et des nombres supérieurs à 3
Donc, pour surmonter le double comptage, nous devons soustraire la probabilité que les deux événements se produisent simultanément (dans cet exemple, la probabilité d’obtenir un nombre qui est à la fois pair ET supérieur à 3) de la probabilité totale obtenue en additionnant les probabilités des événements individuels.
| [latex]\begin{equation} P(\textrm{even } \cup > 3) = \frac{3}{6} + \frac{3}{6} - \frac{2}{6} = \frac{4}{6} = \frac{2}{3} \end{equation}[/latex] | (6.53) |
Plus généralement, on parle de règle d’addition, qui prend la forme générale :
| [latex]\begin{equation} P(A \cup B) = P(A) + P(B) - P(A \cap B) \end{equation}[/latex] | (6.54) |
Dans le cas où deux résultats ne peuvent pas se produire simultanément (c’est-à-dire qu’il n’y a pas de chevauchement dans le diagramme de Venn), alors [latex]P(A \cup B) = P(A) + P(B)[/latex], comme [latex]P(A \cap B) = 0[/latex]. Ceci est connu comme des événements mutuellement exclusifs.
Enfin, supposons que nous modifions légèrement nos critères pour nous intéresser à la probabilité d’obtenir à la fois un nombre pair ET un nombre supérieur à 3 lors d’un lancer de dé. Vous avez peut-être remarqué que nous avons déjà utilisé la probabilité que les événements « nombre pair » et « nombre supérieur à 3 » se produisent simultanément dans l’équation précédente pour calculer la probabilité que l’un des deux événements se produise, [latex]P(\textrm{even } \cap > 3) = \frac{2}{6} = \frac{1}{3}[/latex]. Effectivement, dans cet exemple avec un petit nombre de résultats possibles, il est relativement simple de compter directement le nombre de résultats qui satisfont nos critères. Cependant, dans des scénarios plus complexes, le calcul de probabilité peut devenir plus difficile.
Donc, pour commencer à réfléchir à la question de savoir comment calculer la probabilité que deux événements se produisant simultanément, nous pouvons d’abord demander quelle est la probabilité que l’un des événements se produise, étant donné que l’autre événement s’est déjà produit. Dans cet exemple, nous pourrions calculer la probabilité d’obtenir un nombre supérieur à 3, étant donné que le nombre obtenu est déjà pair. Autrement dit, si nous avons déjà lancé le dé et savons que le résultat est un nombre pair, quelle est la probabilité qu’il soit aussi supérieur à 3?
Nous savons déjà qu’il y a trois faces du dé qui ont des nombres pairs (2, 4 ou 6). Cela signifie que notre nombre de résultats possibles, si nous savons que le résultat est pair, est réduit de 6 à 3. On peut alors compter le nombre de résultats de cet ensemble qui sont supérieurs à 3. Cela nous donne deux résultats (4 et 6). Ainsi, la probabilité de lancer un nombre supérieur à 3, étant donné qu’il est aussi pair est :
| [latex]\begin{equation} P(>3 | \textrm{even}) = \frac{2}{3} \end{equation}[/latex] | (6.55) |
Cependant, ce calcul surestime encore la probabilité que les deux événements se produisent simultanément, car nous avons réduit notre scénario à celui où nous sommes déjà certains à 100% qu’un des résultats s’est produit (nous avons déjà supposé que le résultat du lancer est un nombre pair). Donc, pour remédier à cela, nous pouvons alors multiplier cette équation par la probabilité globale d’obtenir un nombre pair lors du lancer, que nous avons déjà mentionnée précédemment comme étant[latex]P = \frac{3}{6}[/latex].
| [latex]\begin{equation} P(\textrm{even } \cap >3) = \frac{3}{6} \times \frac{2}{3} = \frac{6}{18} = \frac{1}{3} \end{equation}[/latex] | (6.56) |
Cela nous donne la même valeur, [latex]P(A \cap B) = \frac{1}{3}[/latex] que nous avons vu dans notre équation précédente. Ceci est également appelé la règle de multiplication, avec la forme générale :
| [latex]\begin{equation} P(A \cap B) = P(A)P(B|A) \end{equation}[/latex] | (6.57) |
Un autre aspect à prendre en compte lors du calcul de la probabilité est de déterminer si les événements sont dépendants ou indépendants. Dans l’exemple des dés, ces événements sont dépendants, car le fait qu’un événement se produise (obtenir un nombre pair) affecte la probabilité de l’autre événement (obtenir un nombre supérieur à 3). La probabilité globale d’obtenir un nombre supérieur à 3 est [latex]\frac{1}{2}[/latex] , mais augmente à [latex]\frac{2}{3}[/latex] si nous savons déjà que le nombre obtenu est pair.
Si les événements sont indépendants, ce qui signifie qu’ils n’affectent pas la probabilité de se produire mutuellement, la règle de multiplication se simplifie à :
| [latex]\begin{equation} P(A \cap B) = P(A) \times P(B) \end{equation}[/latex] | (6.58) |
La règle de multiplication constitue également la base du théorème de Bayes, qui sera abordé dans la section suivante.
6.5.2 Théorème de Bayes
Le théorème de Bayes est un principe important utilisé en intelligence artificielle pour calculer la probabilité des prochaines étapes d’un robot en tenant compte des étapes qu’il a déjà exécutées. Le théorème de Bayes est défini par :
| [latex]\begin{equation} P(A \cap B) = \frac{P(A)P(B|A)}{P(B)} \end{equation}[/latex] | (6.59) |
Les robots, et parfois les humains, sont dotés de capteurs bruyants et ont une connaissance limitée de leur environnement. Imaginons un robot mobile utilisant la vision pour détecter des objets et sa propre position. Lorsqu’il détecte un four, il peut utiliser cette information pour déduire sa propre position. Ce que nous savons, c’est que la probabilité de voir un four dans une salle de bain est assez faible, tandis qu’elle est élevée dans une cuisine. C’est là que le théorème de Bayes entre en jeu. Vous n’êtes pas certain à 100% de cela, car il est possible que vous l’ayez récemment acheté et l’ayez laissé dans le salon, ou que vos capacités visuelles soient altérées (vos capteurs de vision sont bruyants et peu fiables). Dans ce contexte, il est raisonnable de supposer que, étant donné que vous avez vu un four, il est « plus probable » que vous soyez dans une cuisine plutôt que dans une salle de bain. Le théorème de Bayes offre un mécanisme (mais pas le seul) pour effectuer ce type de raisonnement.
[latex]P(room)[/latex] est la croyance « antérieure » avant que vous n’avez vu le four, [latex]P(oven|room)[/latex] fournit la probabilité de voir un four dans une pièce, et [latex]P(room|oven)[/latex] est votre nouvelle croyance après avoir vu le four. Ceci est également appelé la probabilité « postérieure », la probabilité conditionnelle qui résulte après avoir examiné les preuves disponibles (dans ce cas, une observation du four).
6.5.3 Distribution gaussienne
En effet, dans la réalité, les événements n’ont pas toujours la même probabilité de se produire.
Lorsque différents résultats ont des probabilités différentes de se produire, nous pouvons envisager ces probabilités en termes de fréquences. Plus précisément, nous pouvons nous demander, sur un certain nombre de répétitions d’un événement, à quelle fréquence un résultat spécifique est susceptible de se produire? Nous pouvons tracer ces fréquences sur un histogramme de fréquence, qui compte le nombre de fois que chaque événement s’est produit. Cette logique constitue la base des statistiques fréquentistes, dont nous discuterons plus en détail dans la Section 6.7.
La distribution gaussienne, également connue sous le nom de distribution normale ou « courbe en cloche », désigne une distribution de fréquence ou un histogramme de données dans lequel les points de données sont répartis de manière symétrique. Cela signifie qu’il y a un « pic » dans la distribution, représentant la moyenne, où la plupart des valeurs de l’ensemble de données se situent. Ensuite, la distribution diminue symétriquement de chaque côté à mesure que les valeurs deviennent moins fréquentes (voir la Figure 6-8). De nombreux ensembles de données d’origine naturelle suivent une distribution normale, par exemple la taille moyenne de la population, les résultats des tests à de nombreux examens et le poids des sauterelles lubber.
En robotique, on observe une distribution normale sur la sortie de plusieurs capteurs. En fait, le théorème central limit suggère qu’avec un échantillon suffisamment grand, de nombreuses variables tendront vers une distribution normale, (même si elles ne suivaient pas initialement une distribution normale). Cela en fait un point de départ utile pour de nombreuses analyses statistiques.
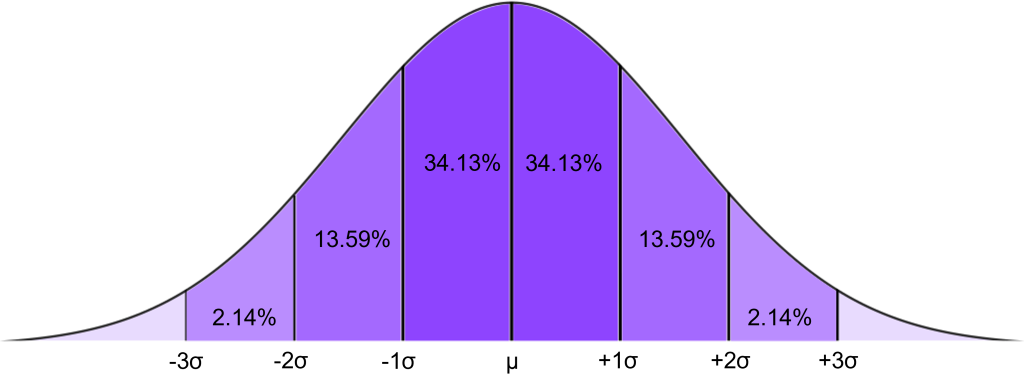
Figure 6-8 : La distribution normale
Nous pouvons utiliser la distribution normale pour prédire la probabilité qu’un point de données se situe dans une certaine zone sous la courbe. Plus précisément, si nos données suivent une distribution normale, nous savons que 68,27% des points de données se situeront à moins de 1 écart-type de la moyenne, 95,45% se situeront à moins de 2 écarts-types, et 99,73% se situent à moins de 3 écarts-types. En termes de probabilité, nous pourrions exprimer cela en disant « qu’il y a une probabilité de 68,27% qu’une valeur choisie au hasard se situe à moins d’un écart-type de la moyenne ». Plus une valeur s’éloigne de la moyenne (le sommet de la courbe), moins sa probabilité d’occurrence est élevée. La probabilité totale de toutes les valeurs de la distribution normale (c’est-à-dire l’aire totale sous la courbe) est égale à 1.
Mathématiquement, l’aire sous la courbe est représentée par une fonction de densité de probabilité, où la probabilité de tomber dans un intervalle donné est égale à l’aire sous la courbe pour cet intervalle. En d’autres termes, nous pouvons utiliser la distribution normale pour calculer la densité de probabilité de voir une valeur, [latex]x[/latex], étant donné la moyenne, [latex]\mu[/latex], et l’écart-type, [latex]\sigma^2[/latex].
| [latex]\begin{equation} p(x|\mu,\sigma^2) = \frac{1}{{\sqrt{2\pi\sigma^2}}}e^{-\frac{1}{2}\frac{(x-\mu)^2}{2\sigma^2}} \end{equation}[/latex] | (6.60) |
Nous pouvons constaté qu’il n’y a en fait que deux paramètres qui doivent être saisis, [latex]\mu[/latex] et [latex]\sigma^2[/latex]. La simplicité de cette représentation est également pertinente pour les applications en informatique et en robotique.
Dans une distribution normale standard, la moyenne est de 0 et l’écart type est de 1. La moyenne et l’écart type de n’importe quel jeu de données distribué normalement peuvent ensuite être transformés pour s’adapter à ces paramètres à l’aide de la formule suivante :
| [latex]\begin{equation} z = \frac{x - \mu}{\sigma} \end{equation}[/latex] | (6.61) |
Ces valeurs transformées sont appelées scores z. Ainsi, si nous avons la moyenne et l’écart type de tout ensemble de données normalement distribué, nous pouvons le convertir en z-scores.
Ce processus est connu sous le nom standardisation et il est utile, car il nous permet d’utiliser les propriétés mentionnées précédemment de la distribution normale pour déterminer la probabilité qu’une valeur spécifique se produise dans n’importe quel ensemble de données qui suit une distribution normale, indépendamment de sa moyenne et de son écart type réels.
C’est parce que chaque z-score est associé à une probabilité spécifique de se produire (nous connaissons déjà les probabilités pour les z-scores à exactement 1, 2 et 3 écarts-types audessus/en dessous de la moyenne). Vous pouvez tout vérifier toutes les probabilités de score z en utilisant les z-tables [10]. à partir de ces z-tables, nous pouvons calculer le pourcentage de la population qui tombe soit au-dessus ou au-dessous d’un certain z-score. Un z-score peut alors être considéré comme une statistique de test représentant la probabilité qu’un résultat spécifique se produise dans un ensemble de données (normalement distribué). Cette étape devient particulièrement importante lors de la réalisation de statistiques inférentielles, qui seront traitées plus en détail dans la suite de ce chapitre.
6.6 Dérivés
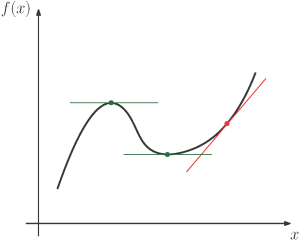
Figure 6-9 : La dérivée d’une fonction donne la pente instantanée de cette fonction. Les emplacements à dérivée nulle sont en représentés en vert : les optimums.
Le calcul différentiel joue un rôle fondamental dans de nombreux concepts mathématiques en robotique, allant de la recherche de gains optimaux à la linéarisation de systèmes dynamiques complexes. La dérivée d’une fonction [latex]f(x)[/latex]est la vitesse à laquelle sa valeur change.
Il peut être approximé par [latex]f'(x)=\frac{\Delta f(x)}{\Delta x}[/latex] . Cependant, plusieurs fonctions algébriques ont des dérivées exactes connues, comme [latex]\dfrac{dx^{n}}{dx}=nx^{n-1}[/latex]. En robotique, nous manipulons des dérivées pour des variables physiques telles que la vitesse ([latex]\dot{x}[/latex]), la dérivée de la position [latex](x)[/latex], et l’accélération ([latex]\ddot{x}[/latex]), la dérivée de la vitesse. En plus de cela, la dérivée peut être utile pour trouver une fonction optimale : lorsque la dérivée d’une fonction est égale à zéro, nous sommes soit à un minimum (local) soit à un maximum (local) (voir la Figure 6-9). Plusieurs propriétés sont utiles à retenir, comme l’opérateur de dérivée qui peut être distribué sur l’addition :
| [latex]\begin{equation} [f(x)+g(x)]'=f'(x)+g'(x), \end{equation}[/latex] | (6.62) |
et réparti sur des fonctions imbriquées :
| [latex]\begin{equation} f(g(x))'=f'(g(x))g'(x) \end{equation}[/latex] | (6.63) |
Enfin, les opérateurs dérivés peuvent être distribués sur une fonction multivariée, en utilisant des dérivées partielles, c’est-à-dire les dérivées par rapport à chaque variable indépendamment.
Par exemple :
| [latex]\dfrac{\partial \left[ Ax_{1}+Bx_{2}\right] }{\partial x_{1}}=A[/latex] | (.6.64) |
6.6.1 Série Taylor
La robotique implique la tentative de contrôler des systèmes dynamiques complexes dans des environnements dynamiques complexes. Dans la plupart des cas, ces systèmes et modèles présentent des dynamiques non linéaires. Par exemple, les forces de traînée sur les avions et les sous-marins ont un impact sur l’accélération du véhicule en fonction du carré de sa vitesse.
Une manière de faire face à cette complexité est de simplifier l’équation en utilisant une approximation polynomiale, qui consiste à additionner différentes puissances de la variable.
La plus populaire est certainement la série Taylor :
| [latex]\begin{equation} f(x)\rvert_a=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+... \end{equation}[/latex] | (6.65) |
qui approxime [latex]f(x)[/latex] autour du point [latex]x = a[/latex] en utilisant une combinaison de ses dérivés. Si nous voulons que notre approximation linéarise la fonction, nous ne garderons que les deux premiers termes :
| [latex]\begin{equation} f(x)\approx f(a)+f'(a)(x-a) \end{equation}[/latex] | (6.66) |
6.6.2 Jacobien
Maintenant, au lieu d’une seule fonction dépendant d’une seule variable, vous vous retrouverez souvent avec un ensemble d’équations dépendant chacune de plusieurs variables. Par exemple :
| [latex]\begin{equation} f_1=Axy,~f_2=Cy^2+Dz,~and~f_3=E/x+Fy+Gz \end{equation}[/latex] | (6.67) |
qui peut s’écrire sous forme de vecteur :
| [latex]\begin{equation} \mathbf{F}=\begin{bmatrix}f_1\\f_2\\f_3\end{bmatrix} \end{equation}[/latex] | (6.68) |
Vous pouvez linéariser ce système d’équations en utilisant la série de Taylor :
| [latex]\begin{equation} \mathbf{F}\approx \mathbf{F}(a)+\mathbf{J}\begin{bmatrix}x-x_a\\y-y_a\\z-z_a\end{bmatrix}, \end{equation}[/latex] | (6.69) |
où [latex]\mathbf{J}[/latex] est la matrice des dérivées partielles des fonctions, souvent appelée jacobienne, dans ce cas :
| [latex]\begin{align} \mathbf{J} = \begin{bmatrix}\dfrac{\partial f_1}{\partial x} & \dfrac{\partial f_1}{\partial y} & \dfrac{\partial f_1}{\partial z}\\ \dfrac{\partial {f_2}}{\partial x} & \dfrac{\partial {f_2}}{\partial y} & \dfrac{\partial {f_2}}{\partial z} \\ \dfrac{\partial {f_3}}{\partial x} & \dfrac{\partial {f_3}}{\partial y} & \dfrac{\partial {f_3}}{\partial z} \end{bmatrix}=\begin{bmatrix}Ay & Ax & 0\\ 0 & 2Cy & D\\ -E/x^2 & F & G\end{bmatrix} \end{align}[/latex] | (6.70) |
Dans le chapitre 10, le jacobien est utilisé comme une matrice pour établir la relation entre l’espace des tâches (vitesses des effecteurs terminaux) et l’espace articulaire (vitesses des actionneurs). Une matrice jacobienne dérivée pour une seule fonction, c’est-à-dire une matrice avec une seule ligne, est appelée un gradient; noté (pour une fonction géométrique dans l’espace cartésien) :
| [latex]\begin{equation} \mathbf{\nabla}f=\begin{bmatrix}\dfrac{\partial f}{\partial x} & \dfrac{\partial f}{\partial y} & \dfrac{\partial f}{\partial z}\end{bmatrix} \end{equation}[/latex] | (6.71) |
Le gradient est un outil utile pour trouver l’optimum d’une fonction en en voyageant dessus; une approche stochastique très utile en apprentissage automatique (voir le chapitre 15).
6.7 Statistiques de base
Lorsque vous menez des recherches en robotique, notamment des études sur les utilisateurs, il est courant de disposer de données que vous avez collectées dans le but de répondre à une question de recherche spécifique. En règle générale, ces questions de recherche s’articulent autour de la relation entre une variable indépendante et une variable dépendante. Par exemple, vous pourriez vous poser la question de savoir comment le nombre de drones (variable indépendante) dans une mission affecte la charge de travail cognitive de l’opérateur (variable dépendante). Il est essentiel de pouvoir analyser les données que vous avez collectées afin de communiquer les résultats de votre recherche. Le chapitre 13 fournira plus de détails sur la conception et la conduite d’études sur les utilisateurs. Pour l’instant, nous allons commencer à expliquer certaines des analyses que vous pouvez effectuer une fois que vous avez obtenu quelques données!
La première étape de l’analyse d’un ensemble de données consiste généralement à décrire ses propriétés d’une manière significative pour votre public (statistiques descriptives).
Cela implique de prendre les données brutes et de les transformer (par exemple, en visualisations ou en statistiques récapitulatives). La deuxième étape consiste ensuite à déterminer comment vous pouvez utiliser vos données pour répondre à une question de recherche spécifique et/ou généraliser les résultats à une population plus large (statistiques déductives). Ici, il est important de faire la distinction entre un échantillon de données collectées, et la population dont les données sont destinées à être généralisées (voir également le chapitre 13). De manière critique, les statistiques descriptives se rapportent uniquement à l’échantillon réel de données que vous avez collectées, tandis que les statistiques inférentielles tentent de faire des généralisations à l’ensemble de la population. En règle générale, les formules utilisées pour calculer les valeurs d’un échantillon font appel à des lettres grecques, tandis que les formules utilisées pour une population font appel à des lettres romaines. Vous trouverez ci-dessous un tableau avec certaines des notations les plus courantes pour les échantillons et les populations.
| Paramètre | Échantillon | Population |
| Moyenne | [latex]\overline{x}[/latex] | [latex]\mu[/latex] |
| Écart-type | [latex]s[/latex] | [latex]\sigma[/latex] |
| Variance | [latex]s^2[/latex] | [latex]\sigma^2[/latex] |
| Nombre de points de données | [latex]n[/latex] | [latex]N[/latex] |
Tableau 6-2 : Notations des paramètres communs pour les échantillons par rapport aux populations
Lorsque nous recueillons des données, nos échantillons peuvent être soit indépendants (les données proviennent de deux groupes de personnes différents), soit répétés (du même groupe).
Prenons l’exemple où nous souhaitons tester les connaissances des étudiants en robotique en ce qui concerne la géométrie de base et l’algèbre linéaire. Nous pourrions soit prendre un seul échantillon d’étudiants et tester leurs connaissances avant et après la lecture de ce chapitre – ce serait une étude au sein des groupes, car les mêmes étudiants ont été testés à chaque fois.
Alternativement, nous pourrions prendre un échantillon d’étudiants qui ont lu ce chapitre du livre et les comparer à un échantillon qui n’a pas lu ce chapitre. Il n’y a pas de chevauchement entre ces deux groupes, il s’agit donc d’une conception d’étude entre-groupes.
Vous pouvez d’abord commencer à décrire les propriétés de votre échantillon en utilisant trois mesures de tendance centrale; la moyenne, la médiane et le mode. Le mode représente la valeur de réponse la plus courante dans vos données . En d’autres termes, si vous prenez toutes les valeurs individuelles de votre ensemble de données et comptez combien de fois chacune apparaît, le mode correspond à la valeur qui apparaît le plus grand nombre de fois. Par exemple, imaginons que nous demandions à 10 professeurs de robotique combien de robots ils ont dans leur laboratoire (voir le Tableau 6-3).
| ID de professeur | Nombre de robots |
|
1 2 3 4 5 6 7 8 9 10 |
1 5 7 10 10 12 12 12 15 20 |
Tableau 6-3 : Exemple de données de robots par professeur
Nous pouvons voir que la valeur la plus courante signalée est 12 robots – il s’agit du mode.
Le mode peut être plus facilement identifié en créant une distribution de fréquence des valeurs dans votre ensemble de données (voir la Figure 6-10).
La médiane est la valeur qui se situe au milieu de votre plage de valeurs. En utilisant l’exemple ci-dessus, si nous avons classé le nombre de robots dans chaque laboratoire du plus petit au plus grand, la médiane est la valeur qui tombe exactement au milieu (ou, s’il y a un nombre pair de points de données, la somme des deux valeurs divisées par 2). Dans ce cas particulier, nous avons 10 valeurs, donc la médiane est la moyenne des 5e et 6e valeurs, [latex]\frac{10 + 12}{2} = 11[/latex].
Cependant, la médiane et le mode se basent tous les deux sur des valeurs uniques, ce qui signifie qu’ils ne tiennent pas compte d’une grande partie des informations disponibles dans un ensemble de données. La mesure finale de la tendance centrale est alors la moyenne, qui prend en compte toutes les valeurs des données en additionnant le total de toutes les valeurs et en les divisant par le nombre total d’observations. La formule pour calculer la moyenne d’un échantillon est exprimée comme suit :
| [latex]\begin{equation} \bar{x} = {\frac{\sum_{i=1}^Nx_i}{n}} \end{equation}[/latex] | (6.72) |
Où [latex]\bar{x}[/latex] représente la moyenne de l’échantillon, [latex]x[/latex] représente une valeur individuelle, et [latex]n[/latex] représente le nombre de valeurs dans l’ensemble de données.
Dans notre exemple, ce serait :
| [latex]\begin{equation} \bar{x}_{robots} = \frac{1 + 5 +7 + 10 + 10 + 12 + 12 + 12 + 15 + 20}{10} = 10.4 \end{equation}[/latex] | (6.73) |
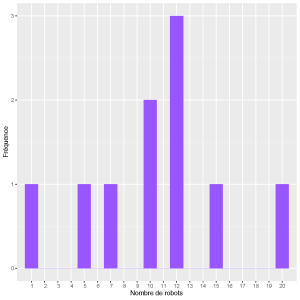
Figure 6-10 : Distribution de fréquence du nombre de robots par laboratoire
Contrairement à la médiane et au mode, cette valeur ne doit pas nécessairement exister dans l’ensemble de données (par exemple, si le nombre moyen de robots dans le laboratoire est en fait de 10,4, certains étudiants ont probablement des questions à répondre…)
De nombreuses statistiques de base peuvent être calculées en utilisant Python avec la bibliothèque numpy :
import numpy as np # Importation des bibliotheques
mu = np.mean(data) # Moyenne de echantillon de donnees
mod = np.mode(data) # Mode de echantillon de donnees
med = np.median(data) # Mode de echantillon de donnees
Dans la distribution normale classique, la moyenne, la médiane et le mode sont égaux.
Cependant, dans la vie réelle, les données ne sont souvent pas parfaitement conformes à cette distribution, ainsi, ces mesures peuvent différer les unes des autres. En particulier, alors que la médiane et le mode sont relativement robustes aux valeurs extrêmes (valeurs aberrantes), la valeur de la moyenne peut changer considérablement. Par exemple, supposons que notre échantillon comprenne un professeur travaillant avec des microrobots qui déclare avoir des centaines de robots dans son laboratoire. Cela fausserait considérablement la moyenne, tout en étant peu représentatif de la majorité de l’échantillon.
Imaginons maintenant que nous ayons demandé à 90 autres professeurs de robotique le nombre de robots dont ils disposent. Nous avons donc maintenant échantillonné un total de 100 professeurs de robotique. Nos résultats montrent maintenant la distribution de fréquence illustrée à la Figure 6-11.
Nous pouvons voir que bien que la moyenne soit toujours de 10,4, le mode est maintenant de 8 robots et la médiane de 10. Ces valeurs, bien qu’étant similaires, ne sont pas identiques, même si les données suivent une distribution normale. Nous pouvons le vérifier en utilisant la fonction de densité de probabilité. Une fois de plus, la distribution normale ne représente pas parfaitement les données, mais elle offre une très bonne approximation des données.
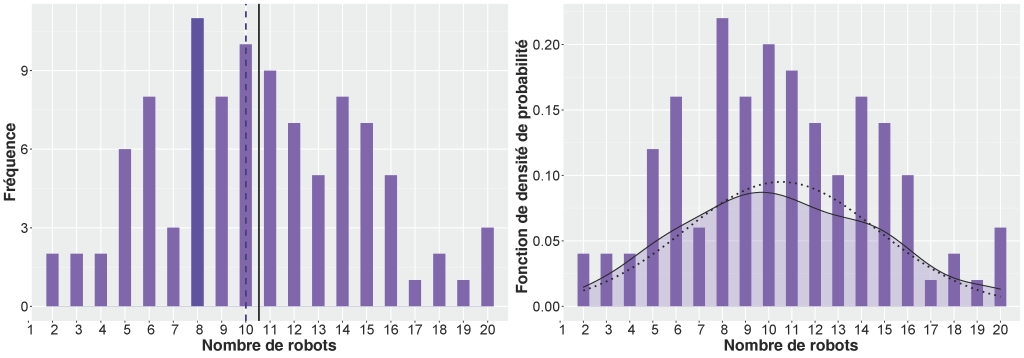
Figure 6-11 : Histogramme de fréquence et fonction de la densité de probabilité pour un ensemble de données distribuées normalement. Le graphique de gauche illustre les mesures de tendance centrale, où la barre violette foncée représente le mode, la ligne violette pointillée représente la médiane et la ligne noire pleine représente la moyenne. Le graphique de droite montre la distribution de probabilité réelle des données en contraste avec une distribution normale.
6.7.1 Variance
La sensibilité de nos métriques descriptives d’ensemble de données à de nouveaux points de données peut être appréhendée en termes de variabilité. Nous pouvons mesurer la quantité de variance dans un échantillon donné, ainsi que détecter les valeurs aberrantes, de plusieurs manières différentes. La première est l’écart-type. Cela représente en moyenne l’écart entre les valeurs et la moyenne. Plus l’écart type est petit, plus les valeurs de l’échantillon sont en moyenne proches de la moyenne et plus la moyenne est précise pour représenter l’échantillon.
Nous pouvons également utiliser l’écart type pour créer un seuil pour les valeurs extrêmes – toute valeur supérieure ou inférieure à 3 écarts types par rapport à la moyenne est susceptible d’être une valeur aberrante (c’est-à-dire non représentative de la population) et peut souvent être exclue.
Pour calculer l’écart type d’une variable, nous prenons d’abord chaque valeur individuelle et en soustrayons la moyenne, ce qui donne une plage de valeurs représentant les écarts par rapport à la moyenne. L’ampleur totale de ces écarts est égale à la variance totale de l’échantillon. Cependant, étant donné que certaines valeurs individuelles peuvent être supérieures à la moyenne et d’autres inférieures, nous devons mettre ces écarts au carré afin qu’ils soient tous positifs, pour éviter que les valeurs positives et négatives ne se compensent mutuellement. Nous additionnons ensuite les écarts au carré pour obtenir une valeur totale de l’erreur dans les données de l’échantillon (appelée somme des carrés). Ensuite, nous divisons par le nombre de points de données dans l’échantillon [latex](n)[/latex], moins un. Parce que nous calculons la moyenne de l’échantillon, et non la moyenne de la population, [latex]n − 1[/latex] représente le degrés de liberté dans l’échantillon. En effet, nous connaissons à la fois la moyenne de l’échantillon et le nombre de points de données. Ainsi, si nous avons les valeurs de tous les points de données sauf un, le dernier point de données ne peut être que la valeur nécessaire pour obtenir cette moyenne spécifique. Par exemple, si nous revenons à notre premier échantillon de 10 professeurs de robotique, et prenons les valeurs des 9 premiers, sachant que la moyenne est de 10,4 et que nous avons échantillonné 10 professeurs de robotique au total, le nombre de robots dans le labo du dernier professeur doit avoir une valeur fixe.
| [latex]\begin{equation} \begin{split} 10.4 =& \frac{1 + 5 + 7 + 10 + 10 + 12 + 12 + 12 + 15 + x}{10} \\ x =& 20 \end{split} \end{equation}[/latex] | (6.74) |
C’est-à-dire que cette valeur de [latex]x[/latex] n’est pas libre de varier. Ainsi, les degrés de liberté sont toujours inférieurs au nombre de points de données dans l’échantillon.
Enfin, après avoir initialement élevé au carré nos valeurs de déviance, nous prenons la racine carrée de l’ensemble de l’équation afin que l’écart type soit toujours exprimé dans les mêmes unités que la moyenne.
Ci-dessous, la formule complète de calcul de l’écart type d’un échantillon. Veuillez noter que si nous devions calculer l’écart-type de la moyenne de la population à la place, la première partie serait remplacée par [latex]\frac{1}{N}[/latex], plutôt que par [latex]\frac{1}{n - 1}[/latex].
| [latex]\begin{equation} s=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2} \end{equation}[/latex] | (6.75) |
En Python, nous pouvons calculer cela en utilisant :
import numpy as np # Importation des bibliotheques
stddev = np.std(data) # Ecart type de echantillon ‘data’
Si nous ne prenons pas la racine carrée de l’équation et la laissons telle quelle, cela s’appelle la variance, noté par [latex]s^2[/latex].
Dans le cadre des tests statistiques, notre intérêt réside dans l’explication des facteurs à l’origine de la variation autour de la moyenne. Dans ce contexte, la moyenne peut être perçue comme un modèle extrêmement simplifié des données, tandis que la variance indique dans quelle mesure ce modèle décrit nos données. Les moyennes présentant une variance élevée sont une représentation peu fiable des données, tandis que celles avec une variance très faible ont de fortes chances d’être une bonne représentation.
La variance d’une variable donnée est composée de deux sources différentes; variance systématique, qui est la variance qui peut être expliquée (potentiellement par une autre variable), et variance non systématique, ce qui est dû à une erreur dans nos mesures.
Nous avons donc souvent, dans nos expériences, plus d’une variable, et nous pourrions être intéressés à décrire la relation entre ces variables – c’est-à-dire que lorsque les valeurs d’une variable changent, les valeurs de l’autre variable changent aussi? Ceci est connu sous le nom de covariance.
La variance totale d’un échantillon à deux variables est alors constituée de la variance attribuée à la variable x, de la variance attribuée à la variable y, et la variance attribuée aux deux. En se souvenant que la variance est simplement le carré de la formule de l’écart type, ou [latex]s^2[/latex], nous pouvons encadrer la somme de la variance totale pour deux variables comme :
| [latex]\begin{equation} (s_x + s_y)^2 = {s_x}^2 + {s_y}^2 + 2s_{xy} \end{equation}[/latex] | (6.76) |
C’est ce dernier terme, [latex]2s_{xy}[/latex] qui nous intéresse, car cela représente la covariance entre les deux variables. Pour calculer cela, nous prenons l’équation de la variance, mais plutôt que de mettre au carré la déviance de [latex]x[/latex], [latex](x - \bar{x})[/latex], nous la multiplions par la déviance de l’autre variable, [latex]y - \bar{y}[/latex]. Cela garantit que nous évitons toujours que les écarts positifs et négatifs s’annulent mutuellement. Ces déviances combinées sont appelées écart de produit vectoriel.
| [latex]\begin{equation} cov(x,y) =\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) \end{equation}[/latex] | (6.77) |
En Python, pour obtenir la covariance entre deux variables, nous pouvons utiliser :
import numpy as np # Importation des bibliotheques
cov = np.cov(data ,ddof=0) #calculer la matrice de covariance
6.7.2 Population générale et échantillons
Dans l’exemple mentionné précédemment, nous nous concentrons sur une population spécifique qui suscite notre intérêt : les professeurs de robotique. Cependant, étant donné la difficulté de tester chaque professeur de robotique dans le monde, nous avons choisi un échantillon restreint de professeurs de robotique et leur avons demandé combien de robots ils avaient dans leurs laboratoires. Dans ce cas, le nombre moyen de robots est une estimation de la moyenne de la population générale. Ceci est différent de la véritable moyenne de la population, qui est la moyenne que nous obtiendrions si nous pouvions réellement demander à chaque professeur de robotique combien de robots il possède. Dans un monde idéal, l’échantillon que vous avez collecté serait parfaitement représentatif de l’ensemble de la population, ce qui signifierait que la moyenne de l’échantillon correspondrait à la véritable moyenne. Cependant, étant donné qu’il y a toujours une certaine marge d’erreur associée aux données, il est probable que la moyenne de l’échantillon diffère légèrement de la véritable moyenne.
Si nous devions prendre plusieurs échantillons différents de professeurs de robotique, chaque échantillon aurait sa propre moyenne et son écart-type, et certains pourraient surestimer ou sous-estimer la véritable moyenne de la population. Si nous représentions graphiquement les moyennes de chaque échantillon dans une distribution de fréquences, le centre de cette distribution serait également représentatif de la moyenne de la population. Il est essentiel de souligner que si la population suit une distribution normale, la distribution des échantillons suivra également une distribution normale. Par conséquent, en connaissant la variance au sein de la distribution des échantillons, nous sommes en mesure d’estimer la probabilité qu’un échantillon particulier soit proche de la véritable moyenne de la population, de la même manière que l’écart type des valeurs individuelles par rapport à la moyenne de l’échantillon permet d’estimer l’erreur dans cet échantillon. L’écart type d’une distribution d’échantillons autour de la moyenne de la population est alors appelé erreur standard, et est exprimé comme.
| [latex]\begin{equation} \label{eq:se} \sigma = \frac{s}{\sqrt{n}} \end{equation}[/latex] | (6.78) |
L’erreur standard nous permet d’estimer la distance moyenne entre la moyenne d’un échantillon choisi au hasard dans la population et la moyenne de la population elle-même.
Bien sûr, lors de nos expérimentations, nous ne sommes généralement pas en mesure de prélever plusieurs échantillons distincts de la population. En général, nous disposons d’un seul échantillon. Cependant, le concept de l’erreur standard revêt une importance théorique pour comprendre comment généraliser nos résultats à partir de notre échantillon à l’ensemble de la population. En revenant au théorème central limite, si la taille de l’échantillon est suffisamment grande, la moyenne de l’échantillon tendra à se rapprocher de la véritable moyenne de la population. En effet, l’erreur standard tend également à se rapprocher de l’erreur standard de la population. Pour cette raison, lors de l’utilisation de statistiques inférentielles, l’erreur standard est souvent préférée à l’écart type.
6.7.3 L’hypothèse nulle
Effectivement, le test d’hypothèse implique de formuler une prédiction concernant nos données, puis de vérifier si cette prédiction est correcte. Généralement, ces prédictions concernent l’existence ou l’absence d’un effet, c’est-à-dire s’il y a une relation entre les variables étudiées ou non.
L’hypothèse nulle, généralement désignée par [latex]H_0[/latex], est l’hypothèse qu’il n’y aura aucun effet présents dans les données. Par exemple, si vous comparez deux robots différents sur certaines caractéristiques (par exemple, l’apparence) et dans quelle mesure l’apparence affecte la sympathie des robots, [latex]H_0[/latex] déclarerait qu’il n’y a pas de différence entre les deux robots. Reliant cela à notre distribution normale, [latex]H_0[/latex] est l’hypothèse que les données des deux groupes proviennent de la même population (c’est-à-dire qu’elles sont représentées par la même distribution, avec la même moyenne). En d’autres termes, le test d’hypothèse nous permet de déterminer s’il y a une différence systématique entre deux échantillons, en évaluant si leurs différences de moyenne et d’écart type sont le résultat du hasard ou si elles reflètent une véritable distinction entre les deux groupes (voir la Figure 6-12) ?
En revanche, l’hypothèse alternative, ou [latex]H_1[/latex], concerne la présence d’un certain effet (dans l’exemple ci-dessus, [latex]H_1[/latex] serait qu’il y a un effet de l’apparence du robot sur la sympathie).
Encore une fois, en mettant cela dans le contexte de la distribution normale, [latex]H_1[/latex] est l’idée que les données proviennent de deux distributions de population différentes, avec des moyennes et des écarts-types différents. Dans ce contexte, le terme « populations » peut également faire référence à des groupes formés dans le cadre d’une manipulation expérimentale. Par exemple, on peut considérer une population de personnes qui ont été exposées à un robot avec des boutons rouges lumineux et émettant des bips agressifs, tandis qu’une autre population a été exposée à un robot avec des lumières colorées et des bips calmes.
Dans les tests inférentiels, nous partons du principe que [latex]H_0[/latex] est vrai par défaut. Ainsi, l’objectif n’est pas de prouver que [latex]H_1[/latex] est vrai, mais plutôt d’essayer de démontrer que [latex]H_0[/latex] est faux. Effectivement, l’objectif est de démontrer qu’il est très peu probable que les deux groupes (ou plus) proviennent de la même distribution de la population.
Ainsi, lorsque nous avons deux moyennes d’échantillons différentes, nous pouvons effectuer un test pour déterminer si les différences entre ces valeurs sont le résultat du hasard (c’est-à dire une variation aléatoire) ou si elles proviennent réellement de populations distinctes. La probabilité que nous aurions obtenu ces données, étant donné que l’hypothèse nulle est vraie, est représentée par la valeur p, voir la Figure 6-13. Typiquement, le seuil de cette probabilité est fixé à 95%. En effet, si nous supposons que l’hypothèse nulle est vraie et que les résultats de
Figure 6-12 : Deux courbes en cloche se chevauchant à partir d’échantillons différents
notre modèle indiquent une probabilité d’observer ces résultats de 5% ou moins, cela suggère que l’hypothèse nulle n’est probablement pas une explication correcte des données.
Dans ce cas, nous rejetons [latex]H_0[/latex] et acceptons [latex]H_1[/latex]. Autrement dit, on appelle le résultat statistiquement significatif. Plus le p-valeur, plus la probabilité que [latex]H_0[/latex] est vrai. Bien que [latex]p < .05[/latex] est le seuil minimal généralement accepté, [latex]p < .01[/latex] et [latex]p < .001[/latex] peuvent également être utilisés.

Figure 6-13 : p-valeurs par rapport à la distribution normale
Veuillez noter que tous ces seuils laissent encore une marge d’erreur – il est possible que nous puissions observer ces résultats même si [latex]H_0[/latex] est vrai, juste peu probable. Effectivement, il est possible de choisir par hasard deux échantillons qui diffèrent considérablement l’un de l’autre (il est important de garder à l’esprit que la distribution des échantillons prélevés dans la population générale suit également une distribution normale, par conséquent, il existe toujours une possibilité d’obtenir un échantillon qui ne représente pas fidèlement la population).
On l’appelle une erreur de Type-I , également connue sous le nom de faux positif – nous avons conclu à tort que les échantillons proviennent de populations différentes, alors qu’en réalité, ils proviennent de la même population. L’inverse de cela, si nous concluons à tort que les échantillons proviennent de la même population, alors qu’en réalité ils proviennent de populations différentes, s’appelle un Type II erreur, voir Tableau 6-4.
Un facteur supplémentaire à prendre en compte lors du réglage du p − value seuil est la directionnalité de notre test. Si nous formulons une prédiction selon laquelle il y aura une différence significative entre les moyennes de nos deux échantillons, nous pourrions choisir
| H0 est vrai | H0 est faux | |
|
Rejeter H0 |
Erreur de type I |
Correct 1 − β |
|
Accepter H0 |
Correct |
Erreur de type II β |
Tableau 6-4 : Erreurs de type I et II
de tester spécifiquement si l’un des échantillons a une moyenne plus élevée que l’autre. Par exemple, nous pourrions effectuer un test pour déterminer si un modèle de robot plus ancien ou plus récent présente des niveaux de performance de batterie différents ou nous pourrions spécifiquement tester si le nouveau modèle a une performance de batterie supérieure à celle de l’ancien modèle. Dans le premier scénario, nous utiliserions test d’hypothèse bilatéral.
Autrement dit, nous ne savons pas de quel côté de la distribution normale notre statistique de test (par exemple, le valeur z) tombera, nous considérons donc les deux. Dans ce dernier scénario, nous spécifions explicitement que la moyenne du nouveau modèle de robot sera supérieure à la moyenne de l’ancien modèle. Ainsi, nous nous concentrons uniquement sur les probabilités associées à cette partie de la distribution en utilisant une statistique de test unilatéral, également appelé test d’hypothèse unilatéral. Cependant, les tests d’hypothèses unilatéraux sont généralement utilisés avec prudence et uniquement dans des contextes où il est logistiquement impossible ou non pertinent d’envisager des résultats dans les deux sens.
En d’autres termes, même si nous avons une hypothèse directionnelle (par exemple, le nouveau modèle a une meilleure performance de batterie), s’il est théoriquement possible que l’ancien modèle ait une meilleure performance de batterie, nous devons également tester les deux extrémités de la distribution de probabilité. Dans cet exemple, si nous utilisions un test d’hypothèse unilatéral en supposant que le modèle le plus récent est meilleur, et qu’en réalité il est pire que l’ancien modèle, il est probable que nous obtenions un résultat non significatif.
Cela nous conduirait à conclure à tort qu’il n’y a pas de différence significative dans les performances de la batterie entre les deux modèles. Pour cette raison, dans la plupart des tests d’hypothèses en robotique, il est préférable d’utiliser des tests bilatéraux.
6.7.4 Le modèle linéaire général
Jusqu’à présent, nous avons discuté des mesures de tendance centrale et des différentes mesures de variance comme moyen de décrire les variables. Cependant, comme mentionné au début de cette section, notre intérêt ne se limite pas seulement à décrire nos données, mais aussi à les utiliser pour prédire un certain résultat. En d’autres termes, notre objectif est de créer un modèle à partir de nos données afin de pouvoir prédire avec précision le résultat pour un ensemble donné de paramètres. Nous pouvons alors conceptualiser tout résultat ou variable que nous essayons de prédire comme une combinaison de la vraie valeur du modèle et de l’erreur associée, de sorte que :
| [latex]\begin{equation} outcome_i = model_i + error_i \end{equation}[/latex] | (6.79) |
Où [latex]Model_i[/latex] peut être remplacée par n’importe quel nombre de variables prédictives. Cela constitue la base du modèle linéaire général. Mathématiquement, ce modèle peut être exprimé par :
| [latex]\begin{equation} Y_i = b + wX_i + \epsilon_i \end{equation}[/latex] | (6.80) |
Où [latex]Y_i[/latex] représente la variable de résultat, [latex]b[/latex] est où tous les prédicteurs sont 0, et [latex]w[/latex] représente la force et la direction d’un effet.
Comme mentionné précédemment, ce processus peut être étendu à un nombre quelconque de variables prédictives. :
| [latex]\begin{equation} Y_i = b_0 + b_1X_i + b_2X_i + ... + b_nX_i + \epsilon_i \end{equation}[/latex] | (6.81) |
Une fois que nous avons défini un modèle, notre objectif est de tester dans quelle mesure il prédit effectivement les données dont nous disposons. Pour évaluer la performance de notre modèle, nous pouvons comparer la quantité de variance dans les données qui est expliquée par notre modèle, divisée par la variance inexpliquée (erreur) pour obtenir différentes statistiques de test. Ensuite, nous pouvons utiliser la distribution normale pour évaluer la probabilité d’obtenir une statistique de test spécifique, étant donné que l’hypothèse nulle est vraie.
| [latex]\begin{equation} \label{eq_test_statistic} \textrm{statistique de test} = \frac{\textrm{variance expliquée par le modèle }}{\textrm{variance inexpliquée (erreur)}} \end{equation}[/latex] | (6.82) |
Pour obtenir le rapport de la variance expliquée à la variance inexpliquée, nous commençons par calculer la variance totale de notre échantillon. Pour ce faire, nous devons revenir à la formule de la somme des carrés, qui est simplement :
| [latex]\begin{equation} SS_{total} = \sum_{i=1}^n(x_i-\bar{x}_{grand})^2 \end{equation}[/latex] | (6.83) |
Où [latex]x_i[/latex]est un point de données individuel, [latex]\bar{x}_{grand}[/latex] est la moyenne générale, ou la moyenne de l’ensemble de données total, et [latex]n[/latex] est le nombre de points de données.
Effectivement, nous savons que la variance peut être calculée en divisant la somme des carrés par les degrés de liberté, ainsi, nous pouvons réorganiser la formule de la somme des carrés comme suit :
| [latex]\begin{equation} \label{eq_SS} \begin{split} s^2 =& \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x}_{grand})^2 \\ s^2 =& \frac{1}{n-1}SS_{total} \\ SS_{total} =& s^2(n-1) \end{split} \end{equation}[/latex] | (6.84) |
Cela nous donne la quantité totale de variation présente dans les données, qui est la somme des écarts de chaque point de données individuel par rapport à la moyenne générale. Nous sommes intéressés à la part de cette variation qui peut être expliquée par notre modèle (en nous rappelant que la variation totale = variation expliquée + variation inexpliquée).
Pour obtenir la quantité de variation expliquée par notre modèle, nous devons ensuite examiner nos moyennes de groupe, plutôt que la moyenne générale. Dans ce cas, notre modèle prédit qu’un individu du groupe A aura une valeur égale à la moyenne du groupe A, un individu du groupe B aura une valeur égale à la moyenne du groupe B. etc.
Nous avons ensuite la possibilité de calculer la déviation de chaque moyenne de groupe par rapport à la moyenne globale, en les mettant au carré (ce qui revient exactement à calculer une somme normale des carrés). Ensuite, nous multiplions chaque valeur par le nombre de participants dans ce groupe. Enfin, nous additionnons toutes ces valeurs.
Donc, si nous avons trois groupes, cela ressemblerait à :
| [latex]\begin{equation} SS_{model} = n_a(\bar{x}_a - \bar{x}_{grand})^2 + n_b(\bar{x}_b - \bar{x}_{grand})^2 + n_c(\bar{x}_c - \bar{x}_{grand})^2 \end{equation}[/latex] | (6.85) |
Où [latex]n_a[/latex] représente le nombre de points de données dans le groupe A, [latex]\bar{x}_a[/latex] représente la moyenne du groupe A, et [latex]\bar{x}_{grand}[/latex] représente la moyenne générale.
Cela peut être étendu à k nombre de groupes avec la forme générale :
| [latex]\begin{equation} SS_{model} = \sum_{n=1}^kn_k({\bar{x}_k}-\bar{x}_{grand})^2 \end{equation}[/latex] | (6.86) |
Où [latex]k[/latex] représente le nombre de groupes, [latex]n_k[/latex] représente le nombre de points de données dans le groupe k, [latex]\bar{x}_k[/latex] représente la moyenne du groupe [latex]k[/latex], et [latex]\bar{x}_{grand}[/latex] représente la moyenne générale.
Maintenant, nous disposons de la variance totale ainsi que de la variance expliquée par notre modèle. Intuitivement, la variance restante correspond à la variance d’erreur, ou la variance qui n’est pas expliquée par le modèle. Cette variance résiduelle représente la différence entre les prédictions de notre modèle (basées sur les moyennes des groupes) et nos données réelles. Bien qu’en théorie, nous puissions obtenir cette valeur en soustrayant la variance du modèle de la variance totale, nous pouvons également la calculer indépendamment.
N’oubliez-pas que notre modèle prédit qu’un individu du groupe A aura un score égal à la moyenne du groupe A. Ainsi, pour calculer la variance résiduelle, nous commençons par calculer la déviance de chaque individu du groupe A par rapport à la moyenne du groupe A, et nous répétons le même processus pour le groupe B et ainsi de suite. Cela peut être exprimé comme suit :
| [latex]\begin{equation} SS_{residual} = \sum_{i=1}^n(x_{ik}-\bar{x}_{k})^2 \end{equation}[/latex] | (6.87) |
Où [latex]n[/latex]représente le nombre total de points de données, [latex]i[/latex]représente un point de données individuel, [latex]x_{ik}[/latex] représente la valeur d’un individu, [latex]i[/latex] en groupe [latex]k[/latex], et [latex]\bar{x}_k[/latex] représente la moyenne de ce groupe.
On peut calculer la déviation de chaque point de données individuel par rapport à sa moyenne de groupe respective, puis les additionner. Cependant, on peut également considérer la variance résiduelle comme la somme de la variance du groupe A, plus la variance du groupe B, et ainsi de suite pour [latex]k[/latex] nombre de groupes. Nous avons également vu précédemment comment la somme des carrés peut être exprimée en termes de variance (voir équation 6.84).
La même logique peut être appliquée ici pour additionner les variances de groupe pour nous donner :
| [latex]\begin{equation} SS_{residual} = \sum s_k^2(n_k-1) \end{equation}[/latex] | (6.88) |
Où [latex]s^2_k[/latex] représente la variance du groupe [latex]k[/latex], et [latex]n_k[/latex] représente le nombre de points de données pour ce groupe.
Visuellement, la somme totale des carrés ([latex]SS_{total}[/latex]), la somme des carrés du modèle ([latex]SS_{model}[/latex]), et la somme résiduelle des carrés ([latex]SS_{residual}[/latex]) peuvent être représentées par les trois valeurs illustrées à la Figure 6-14.
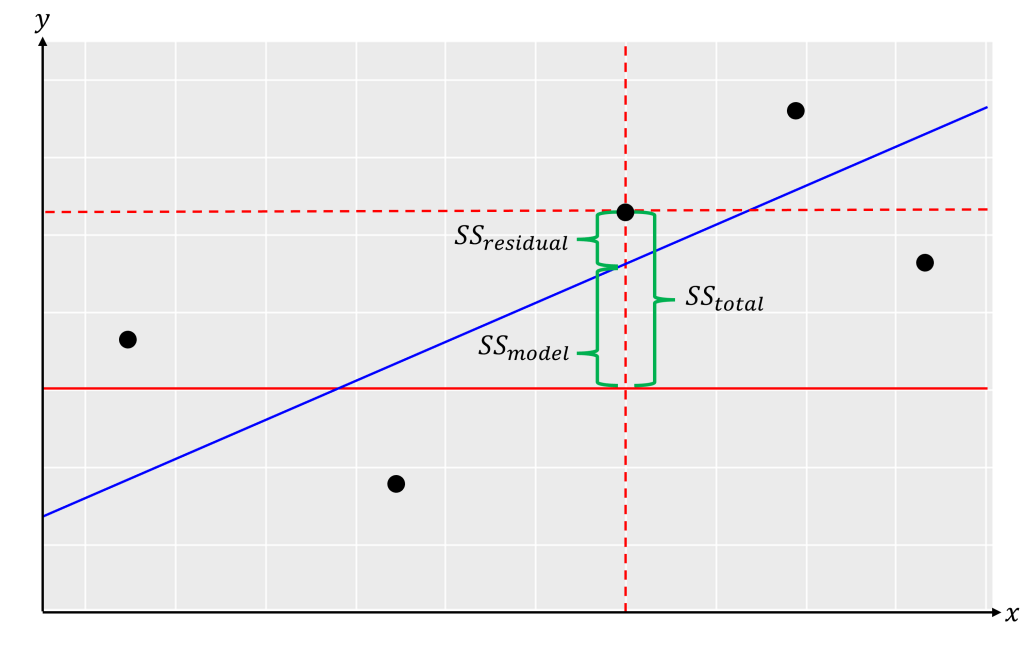
Figure 6-14 : Illustration de la somme totale des carrés, de la somme des carrés du modèle et de la somme résiduelle des carrés. La ligne rouge continue représente la moyenne générale, les lignes rouges pointillées indiquent un point de données spécifique (ou moyenne de groupe) et la ligne bleue continue représente la valeur prédite de y pour une valeur donnée de x.
Cependant, à l’heure actuelle, ces valeurs sont biaisées par le nombre de points de données utilisés pour les calculer. La somme des carrés du modèle est basée sur le nombre de groupes (par exemple, 3), tandis que la somme des carrés totale et résiduelle est basée sur le nombre de points de données individuels (qui pourraient être 5, 15, 50, ou 500). Pour corriger cela, nous pouvons diviser chaque somme de carrés par les degrés de liberté afin d’obtenir les carrés moyens (MS). Pour [latex]MS_{model}[/latex] les degrés de liberté sont égaux au nombre de groupes moins un, alors que pour [latex]MS_{residual}[/latex] ils sont calculés par le nombre total de points de données moins le nombre de groupes.
| [latex]\begin{equation} \label{eq:MS} \begin{split} MS_{model} =& \frac{SS_{model}}{k-1}\\ MS_{residual} =& \frac{SS_{residual}}{n-k} \end{split} \end{equation}[/latex] | (6.89) |
Où [latex]k[/latex] représente le nombre total de groupes et [latex]n[/latex] représente le nombre total de points de données.
À ce stade, nous sommes en mesure de comparer la variance expliquée par notre modèle à la variance résiduelle, également appelée variance d’erreur, et de vérifier si cette relation est significative. Bien qu’il existe de nombreux types de tests statistiques que nous pouvons utiliser pour évaluer la signification de notre modèle, nous nous concentrerons sur seulement deux d’entre eux : le test t et l’ANOVA.
6.7.5 Test t
Effectivement, le test t est utilisé pour comparer les moyennes de deux échantillons distincts afin de déterminer s’il existe une différence statistiquement significative entre eux (moins de 5% de chances d’observer cette différence dans les moyennes étant donné que l’hypothèse nulle est vraie).
Comme nous l’avons vu précédemment dans la section 6.7.2, lorsque les tailles d’échantillon sont suffisamment grandes, la distribution d’échantillonnage d’une population se rapproche de la distribution normale, et nous pouvons utiliser z-scores pour calculer les probabilités (en utilisant p-valeurs associées à des z-scores). Cependant, si nous avons des échantillons de petite taille (ce qui peut souvent être le cas dans les études d’utilisateurs), nous ne pouvons pas estimer de manière fiable la variance de la population. Dans ce cas, nous utilisons une distribution-t, qui est une estimation plus prudente de la distribution normale. C’est la distribution t que nous utilisons pour calculer nos valeurs- p pour le test t. Voir la Figure 6-15 pour une comparaison entre les distributions z et t.
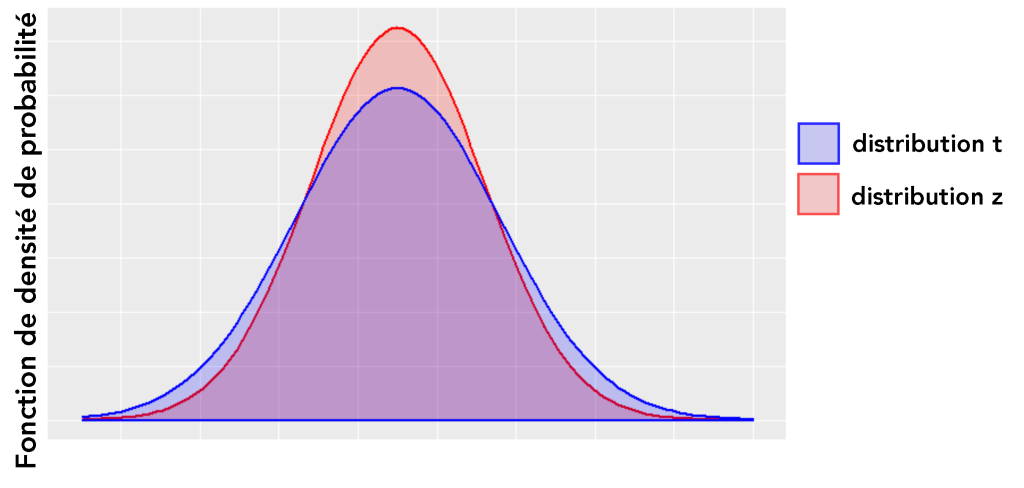
Figure 6-15 : Comparaison des distributions t et z
La valeur du test t est alors une fonction de la moyenne et de l’erreur type des deux échantillons que nous comparons. Effectivement, si nous observons une grande différence entre deux moyennes, il est intuitif de penser qu’il existe une réelle différence entre les échantillons.
Cependant, si l’erreur standard est également élevée et que la différence entre les moyennes est égale ou inférieure à cette valeur, il est peu probable que cette différence soit significative. En effet, la différence entre les moyennes pourrait simplement être due à une grande variance au sein d’une seule population.
Ainsi, pour effectuer un test t, l’objectif est de comparer la différence de moyennes observée entre deux échantillons à la différence de moyennes que l’on s’attendrait à observer si ces échantillons provenaient de la même population (généralement considérée comme étant 0).
Revenons à la section précédente, nous avons également constaté que la statistique de test, dans ce cas le test t, peut être calculée en divisant la variance expliquée par le modèle par la variance d’erreur (voir l’équation 6.82). Dans ce cas, le modèle que nous testons est la différence entre les moyennes réelles et les moyennes attendues. Nous prenons cette valeur (qui, comme la différence attendue entre les moyennes est de 0, n’est en fait que la valeur de la différence observée) et la divisons par l’erreur type des différences entre les moyennes.
Pour calculer l’erreur type des différences entre les moyennes, nous commençons par additionner les variances de chaque échantillon, puis nous divisons cette somme par la taille de chaque échantillon. Ceci est basé sur la loi de la somme des variances, qui stipule que la variance de la différence entre deux échantillons est égale à la somme de leurs variances individuelles.
| [latex]\begin{equation} \frac{{s_1}^2}{n_1} + \frac{{s_2}^2}{n_2} \end{equation}[/latex] | (6.90) |
Nous prenons ensuite la racine carrée de cette valeur pour obtenir l’erreur type de la différence.
| [latex]\begin{equation} \sqrt{\frac{{s_1}^2}{n_1} + \frac{{s_2}^2}{n_2}} \end{equation}[/latex] | (6.91) |
Ainsi, l’équation dans (6.90) devient :
| [latex]\begin{equation} t = \frac{(\bar{x_1} - \bar{x_2})}{ \sqrt{\frac{{s_1}^2}{n_1} + \frac{{s_2}^2}{n_2}}} \end{equation}[/latex] | (6.92) |
Cependant, cela suppose que les tailles d’échantillon de chaque groupe sont égales. Dans le cas où elles ne le sont pas (ce qui est souvent le cas), nous remplaçons [latex]s_1[/latex] et [latex]s_2[/latex] avec une estimation de la variance groupée, qui pondère la variance de chaque échantillon par sa taille d’échantillon.
| [latex]\begin{equation} s^2_{pooled} = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2} \end{equation}[/latex] | (6.93) |
À son tour, la statistique du test t devient :
| [latex]\begin{equation} t = \frac{(\bar{x_1} - \bar{x_2})}{ \sqrt{\frac{{s_{pooled}}^2}{n_1} + \frac{{s_{pooled}}^2}{n_2}}} \end{equation}[/latex] | (6.94) |
Veuillez noter que nous supposons également que les données proviennent de deux groupes différents (c’est-à-dire un test t de groupes indépendants). Lorsque nous avons une conception au sein des groupes, nous utilisons à la place un test t dépendant.
En Python, les tests t pour les échantillons au sein de et entre les groupes peuvent être calculés avec :
from scipy import stats # Bibliotheque importation
res = stats.ttest rel(x1, x2) # Executer le test pour echantillon dependant
res = stats.ttest ind(x1, x2) # Executer le test pour echantillon independant
print(res[1])
Nous pouvons ensuite calculer la probabilité que nous aurions observé cette valeur t si les échantillons provenaient effectivement de la même population, ce qui nous donne la valeur p.
Nous pouvons le faire en utilisant des tables de distribution t ou, puisque nous utilisons probablement une forme de logiciel statistique, lisez cette valeur à partir de la sortie. La chose importante à savoir est que, puisque nos données sont distribuées normalement, la valeur p pour chaque valeur t reste cohérente. Autrement dit, si nous menions deux expériences complètement différentes et que nous nous retrouvions avec le même résultat ou un résultat similaire les valeurs t, et les valeurs-p seraient également les mêmes.
Pour illustrer concrètement, supposons que nous souhaitions comparer deux algorithmes de navigation différents : l’un que nous avons développé et l’autre développé par un laboratoire concurrent, en ce qui concerne leur vitesse de résolution d’un puzzle de labyrinthe (en millisecondes). Nous avons effectué un test t indépendant comparant les deux algorithmes et obtenu les résultats suivants, présentés dans le Tableau 6-5 ci-dessous :
| Moyenne (SD) | Estimation | valeur t | valeur p |
| Algorithme propre Algorithme concurrent | |||
| 1055(408) 4042(605) | -2986.9 | -28.94 | < .001 |
Tableau 6-5 : Test t des groupes indépendants
À partir de là, nous pouvons voir que notre algorithme résout le puzzle beaucoup plus rapidement. Nous pouvons également comparer les distributions de probabilité des deux groupes, voir la Figure 6-16. Cela confirme également qu’il y a très peu de recoupement dans les valeurs observées dans les deux échantillons, et que la probabilité de ces valeurs se produisent est très faible.
Figure 6-16 : Fonction de densité de probabilité pour chaque algorithme
Des exemples supplémentaires de tests t basés sur un ensemble de données public d’enquêtes sur la charge de travail sont disponibles en ligne sous la forme d’un ensemble d’exemples Python [11].
6.7.6 ANOVA
ANOVA est l’abréviation de « Analysis of Variance », et est une extension du test t lorsque nous avons plus de deux groupes. En d’autres termes, nous cherchons à nouveau à comparer les moyennes de différents échantillons afin de déterminer s’il existe une différence statistiquement significative entre eux. Cela signifie déterminer s’ils proviennent de la même distribution de population ou de distributions de population différentes. Pour ce faire, nous utilisons le test F. Le test F est simplement une autre statistique de test qui, comme nous l’avons vu précédemment, mesure la variance totale expliquée par notre modèle par rapport à la quantité d’erreurs présentes dans le modèle.
Pour en savoir plus sur la différence entre un test t, et un test F, imaginez que nous avons 3 groupes différents (A, B et C). Nous avons donc plusieurs résultats possibles différents pour les résultats : Premièrement, il est possible qu’il n’y ait aucune différence significative entre les trois groupes. Deuxièmement, A, B et C pourraient tous être significativement différents les uns des autres. Alternativement, il est possible que le groupe A soit différent du groupe B, mais pas du groupe C, et ainsi de suite pour toutes les combinaisons possibles de A, B et C.
Ainsi, nous pouvons déjà constater qu’il existe davantage d’options par rapport au test t, où nous n’avons que deux groupes et le résultat est binaire – il y a soit une différence significative entre les groupes, soit il n’y en a pas.
Une ANOVA est donc conduite en deux étapes : Dans un premier temps, nous effectuons un test omnibus pour déterminer s’il y a une différence entre les moyennes. Cependant, cela ne nous dit pas quels groupes, en particulier, pourraient être différents les uns des autres.
Ainsi, si le résultat de ce test est significatif, alors nous on procédons à une série de tests t pour chacune des combinaisons bidirectionnelles possibles des groupes. La raison pour laquelle nous ne commençons pas tout de suite avec les tests t est que cela augmente nos chances de commettre une erreur de type I (conclure à tort que les échantillons proviennent de populations différentes alors qu’ils proviennent en réalité de la même population). En effet, si nous fixons notre seuil de signification à 95%, alors nous autorisons toujours un risque de 5% de rejeter à tort l’hypothèse nulle. Si nous effectuons trois tests t indépendamment les uns des autres, chacun avec un seuil de signification de 95%, alors nous pouvons voir comment cette erreur se cumule : [latex]0.95^3 = 0.8571[/latex] et [latex]1−0.857 = 14.3\%[/latex]. Ainsi, au lieu d’avoir un risque de [latex]5\%[/latex] de rejeter à tort l’hypothèse nulle, nous avons maintenant un risque de [latex]14,3\%[/latex]. Ceci est connu sous le nom de taux d’erreur familiale, et il augmente avec le nombre de comparaisons que nous effectuons. En commençant notre analyse par un test omnibus, nous essayons d’atténuer cette erreur.
Pour obtenir la statistique F omnibus, nous devons revenir à l’équation 6.89 où nous pouvons calculer les valeurs de la variance du modèle et de la variance résiduelle!. Ainsi, la statistique F peut être exprimée de la manière suivante :
| [latex]\begin{equation} F = \frac{MS_{model}}{MS_{residual}} \end{equation}[/latex] | (6.95) |
Toute valeur supérieure à 1 indique que notre modèle explique plus de variance que les différences individuelles aléatoires (ce qui est positif!) Cependant, cela ne nous indique toujours pas si cette valeur est significative. Pour vérifier cela, nous retournons à nouveau à nos valeurs p à déterminer, avec une donnée statistique F et des degrés de liberté associés, quelle est la probabilité d’obtenir cette valeur, si l’hypothèse nulle est vraie. Pour obtenir les degrés de liberté, nous devons prendre en compte les deux composantes de notre ratio : la variance du modèle et la variance résiduelle. Nous avons également mentionné précédemment comment la somme des carrés pour chacune de ces composantes était calculée en utilisant leur nombre respectif de points de données – pour la variance du modèle, cela correspond au nombre de groupes, et pour la variance résiduelle, cela correspond au nombre de points de données. Ce sont ces valeurs que nous utilisons pour obtenir les degrés de liberté.
| [latex]\begin{equation} df =\frac{k - 1}{n - k} \end{equation}[/latex] | (6.96) |
Où la valeur k est égale au nombre de groupes et la valeur n est égale à la taille de l’échantillon. C’est aussi pourquoi k−1 est parfois appelé le degrés de liberté du numérateur, alors que [latex]n − k[/latex] s’appelle le degrés de liberté du dénominateur.
Après avoir déterminé nos degrés de liberté et nos valeurs statistiques F, nous devons alors utiliser les tableaux de répartition F (ou notre logiciel de statistiques) pour consulter les valeurs p. Encore une fois, la valeur p pour toutes les valeurs F avec des degrés de liberté spécifiques sera toujours le même.
Après une ANOVA significative, l’étape suivante consiste à effectuer des tests t entre chaque paire de groupes, appelés comparaisons par paires. Cependant, nous devons encore être prudents et éviter d’augmenter notre erreur de type I. Lorsque le nombre de comparaisons est inférieur à 5, il est généralement considéré comme acceptable d’utiliser les valeurs p telles quelles. Cependant, pour tout ce qui est supérieur à ce nombre, il est recommandé d’utiliser une méthode d’ajustement. Cela implique généralement l’application d’une correction aux valeurs p pour rendre leurs estimations plus conservatrices; voir (Bender and Lange, 2001) pour une explication des différents types de corrections.
Maintenant que nous avons abordé une partie de la logique sous-jacente à l’ANOVA, nous pouvons examiner son application pratique. Imaginons que nous disposions d’un échantillon d’opérateurs de robots et que nous souhaitions comprendre la difficulté d’utiliser des robots autonomes pour explorer différents types d’environnements. Pour ce faire, nous concevons une expérience pour étudier comment le type d’environnement affecte la difficulté perçue de la tâche. Ici, notre variable indépendante est l’environnement de la tâche (terre, eau, air) et notre variable dépendante est la difficulté perçue de la tâche, mesurée sur une échelle de 7 points allant de 1 (très facile) à 7 (très difficile). Nous avons testé un total de 150 opérateurs de robots, répartis en 50 individus dans chaque environnement.
Dans ce cas, l’hypothèse nulle ([latex]H_0[/latex]) est qu’il n’y aura pas de différence entre les 3 environnements de tâches. L’hypothèse alternative ([latex]H_1[/latex]) est que la difficulté perçue de la tâche changera en fonction de l’environnement de la tâche.
Après avoir exécuté nos statistiques descriptives, nous observons les moyennes et les écarts types suivants pour chaque groupe, voir le Tableau 6-6.
| Environnement | Moyenne (SD) |
| Terre | 3.12(1.00) |
| Eau | 5.16(0.95) |
| Air | 5.38(1.28) |
Tableau 6-6 : Moyenne et SD pour la difficulté perçue de la tâche dans chaque environnement de tâche
Comme première étape de l’ANOVA, nous effectuons le test omnibus F, pour déterminer s’il y a une différence globale entre les groupes; Tableau 6-7.
| DF | Somme des carrés | Carrés moyens | Valeur F | p | |
| Environnement | 2 | 155.3 | 77.65 | 65.68 | < .001 |
| Résidus | 147 | 173.8 | 1.18 |
Tableau 6-7 : Résultats du test F Omnibus pour l’ANOVA à un facteur
Ce que vous pouvez peut-être observer à partir de ces tableaux, c’est que les valeurs de chaque colonne correspondent exactement aux formules dont nous avons discuté pour le modèle linéaire général. En d’autres termes, les moyennes des carrés sont obtenues en divisant les sommes des carrés par les degrés de liberté pour chaque ligne, et la valeur F est le rapport des moyennes des carrés. Ainsi, même si vous vous retrouvez dans une situation où vous disposez uniquement de vos données expérimentales sans accès à Internet ni à un logiciel statistique téléchargé, vous pouvez toujours calculer vos ANOVA manuellement!
En regardant la valeur p, on peut constater que l’ensemble du test F est significatif ([latex]p < .001[/latex]). Cependant, nous ne savons pas encore quelles sont les différences spécifiques entre les environnements (c’est-à-dire, nous ne savons pas quels environnements sont perçus comme significativement plus ou moins difficiles). Par conséquent, la prochaine étape consiste à comparer les groupes en utilisant des comparaisons par paires. Vous pouvez vous référer au tableau suivant pour voir ces comparaisons : 6.8.
| Estimation | SE | valeur t | valeur p | |
| Terre par rapport à eau
Terre par rapport à air Eau par rapport à air |
-2.04 -2.26 -0.22 |
0.22 0.22 0.22 |
-9.38 -10.39 -1.01 |
< .001 < .001 .313 |
Tableau 6-8 : Comparaisons par paires post-hoc pour chaque environnement de tâche sans correction
À partir de ces résultats, nous pouvons maintenant conclure que les environnements aériens et aquatiques sont perçus comme plus difficiles à explorer que les environnements terrestres, mais il n’y a pas de différence significative entre ces deux environnements. Nous pouvons alors formuler les résultats de ce test de la manière suivante :
Les résultats d’une ANOVA à un facteur entre les groupes ont révélé un effet significatif de l’environnement de la tâche sur la difficulté perçue de la tâche, [latex]F(2, 147) = 65.68, p < .001[/latex]. Des comparaisons post-hoc par paires sans correction indiquent que l’environnement terrestre était perçu comme significativement moins difficile que les environnements aquatique[latex](t = −9.38, p < .001)[/latex] et aérien [latex](t = −10.39, p < .001)[/latex], respectivement. Cependant, il n’y avait pas de différence dans la difficulté perçue de la tâche entre les environnements aquatiques et aériens [latex](t = −1.01, p = .313)[/latex].
Dans l’exemple susmentionné, nous n’avions qu’une seule variable indépendante, l’environnement de la tâche, il s’agit donc d’une ANOVA à un facteur. Maintenant, imaginons que nous élargissions notre conception expérimentale pour inclure non seulement l’environnement de la tâche, mais également le type de robot utilisé pour l’exploration, à savoir les véhicules aériens sans pilote (UAV) par rapport aux véhicules terrestres sans pilote (UGV). Nous avons maintenant deux variables indépendantes : l’environnement de la tâche (avec à nouveau 3 niveaux : terre, eau et air) et le type de robot (UAV par rapport à UGV). Notre variable dépendante, la difficulté perçue de la tâche, reste la même. On l’appelle une ANOVA à deux facteurs.
Dans ce cas, nous avons maintenant deux effets principaux qui nous intéresse ; l’effet du type de robot sur la difficulté de la tâche et l’effet de l’environnement de la tâche. Cependant, il existe également un troisième effet – l’interaction entre les deux variables. Un effet d’interaction indique qu’à différents niveaux d’une variable, l’effet de l’autre variable sur la variable dépendante change. Pour simplifier les choses, ces types d’effets sont appelés… effets simples. La directionnalité des hypothèses d’interaction est généralement déterminée théoriquement et spécifiée avant d’effectuer l’analyse. Cependant, nous ne réalisons généralement qu’un seul ensemble d’analyses (soit l’effet de la variable A à différents niveaux de la variable B, soit l’effet de la variable B à différents niveaux de la variable A, mais pas les deux en même temps). Cela est lié à notre souci de minimiser les chances de commettre une erreur de type I. Rappelez-vous que chaque analyse que nous effectuons comporte un risque de rejet incorrect de l’hypothèse nulle. Ainsi, plus nous effectuons d’analyses, plus ce risque s’accumule.
Dans ce cas, nous examinerons les effets simples du type de robot sur les niveaux de l’environnement de la tâche. En d’autres termes, à chaque niveau de l’environnement de la tâche (terre, eau, air), nous effectuerons une analyse de l’effet du type de robot sur la difficulté perçue de la tâche. Cependant, nous pourrions tout aussi bien dire que selon le type de robot, l’effet de l’environnement de la tâche sur la difficulté perçue de la tâche change.
La syntaxe pour calculer cette analyse en Python ressemble à :
# Importation de la bibliotheque
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova lm
# Creer le modele (deux facteurs − le dernier terme est interaction)
formula = ’task difficulty ~ C(environment) + C(robot) + C(environment):C(robot)’
# Testez le modele par rapport aux donnees (doit avoir des en−tetes de colonne comme dans le modele)
model = ols(formula , data).fit()
# Executer une ANOVA a deux facteurs
aov table = anova lm(model , typ=2)
print(aov table.round(4))
Nous pouvons observer les moyennes et les écarts types pour notre nouvel ensemble de données ci-dessous dans le Tableau 6-9 :
| Environnement | Type de robot | Moyenne (SD) |
|
UAV UGV UAV UGV UAV UGV |
terrestre terrestre aquatique aquatique aérien aérien |
5.12(1.47) 3.20(1.34) 6.16(0.79) 6.00(0.70) 2.92(1.45) 5.08(1.42) |
Tableau 6-9 : Moyennes et SD pour l’environnement de tâche et le type de robot
Donc, pour récapituler, nous avons maintenant deux principaux effets que nous examinons, et un effet d’interaction. Chaque effet principal est associé à une valeur F, tout comme l’interaction. Nous pouvons observer ceux-ci et leurs significations associées dans le tableau ci-dessous (Tableau 6-10).
| DF | Somme des carrés | Moyenne des carrés | Valeur F | p | |
| Environnement | 2 | 133.97 | 66.99 | 43.91 | < .001 |
| Type de robot | 1 | 0.03 | 0.03 | 0.017 | .900 |
| Environnement *Type de robot | 2 | 104.69 | 52.35 | 34.31 | < .001 |
| Résidus | 144 | 219.68 | 1.53 |
Tableau 6-10 : Résultats du test F Omnibus pour l’ANOVA à deux facteurs
Sur la base de ce tableau, nous pouvons constater qu’il existe toujours un effet principal de l’environnement de la tâche, mais pas d’effet principal du type de robot. Cependant, l’interaction entre l’environnement de la tâche et le type de robot est significative.
Comme avec l’ANOVA à un facteur précédente, nous pouvons suivre le F-test significatif pour l’interaction avec des comparaisons par paires. Dans ce cas, nous prenons chaque niveau d’environnement (terre, eau, air) et examinons l’effet du type de robot sur la difficulté de la tâche dans chacune de ces conditions. Étant donné que nous n’avons que 2 niveaux de type de robot (UAV et UGV), nous pouvons passer directement aux tests t pour comparer les UAV et les UGV dans chaque environnement de tâche. Cependant, si nous avions plus de 2 niveaux (par exemple, si nous avions également testé des véhicules sous-marins sans pilote), nous aurions besoin de réaliser une autre ANOVA à un facteur pour chaque type d’environnement, ensuite effectuer des comparaisons par paires entre les types de robots en fonction de l’environnement qui a montré une différence significative.
Les résultats des comparaisons par paires pour l’effet du type de robot dans chaque environnement de tâche sont présentés ci-dessous (Tableau 6-11) :
| Estimation | Valeur t | Valeur p | |
| Terre | 1.92 | 4.78 | < .001 |
| Air |
-2.16 |
-5.41 |
< .001 |
| Eau |
0.16 |
0.749 |
.457 |
Tableau 6-11 : Comparaisons par paires post-hoc pour l’ANOVA à deux facteurs sans correction
Maintenant, les choses commencent à devenir un peu intéressantes. à partir de ce tableau, nous pouvons constater que, dans le milieu aquatique, il n’y a pas de différence entre les UGV et les UAV. En fait, la difficulté moyenne perçue des tâches pour ces deux groupes est assez élevée (probablement parce que ni les UAV ni les UGV ne sont adaptés à l’exploration sous-marine). À l’inverse, dans l’environnement terrestre, l’UGV est évalué comme ayant une difficulté de tâche nettement inférieure à celle du UAV, et vice versa pour l’environnement aérien, où le UAV a une difficulté de tâche inférieure.
Nous pouvons tracer un graphique de cette interaction comme illustré à la Figure 6-17. En observant ce graphique, nous commençons à comprendre pourquoi l’effet principal pour le type de robot n’était pas significatif. Cela est dû au fait que les moyennes pour les UAV et les UGV ont été inversées pour les environnements terrestre et aérien, et similaires pour l’environnement aquatique. Lorsqu’elles sont combinées, ces moyennes s’annulent mutuellement. Ainsi, lorsque nous examinons les moyennes agrégées pour les deux types de robots (voir la Figure 6-18), sans prendre en compte s’ils se trouvaient dans un environnement terrestre, aquatique ou aérien, il ne semble pas y avoir de différence significative entre eux. De plus, en traçant des lignes reliant les moyennes (représentées par des lignes pointillées violettes et vertes), nous observons qu’elles se croisent. Cela indique généralement la présence d’une interaction.
Par conséquent, lorsqu’une interaction est présente, les résultats de cette interaction prennent le pas sur les effets principaux. En d’autres termes, nous pouvons affirmer que les effets principaux étaient conditionnés par la présence d’une interaction. Si aucune interaction significative n’est observée, nous pouvons alors interpréter les effets principaux de la même manière que dans une ANOVA à un facteur.
La rédaction de cette analyse ressemblerait à quelque chose comme :
Figure 6-17 : Interaction à deux facteurs entre l’environnement de tâche et le type de robot
Les résultats de l’analyse de variance à deux facteurs ont révélé un effet principal significatif de l’environnement de la tâche, [latex]F(2, 144) = 43.91, p < .001[/latex], mais pas d’effet principal significatif du type de robot [latex]F(1, 144) = 0.017, p = .900[/latex]. Cependant, ces effets ont été nuancés par la présence d’une interaction entre l’environnement de la tâche et le type de robot, F(2, 144) = 34.31, p < .001. Des tests de suivi pour l’effet simple du type de robot à chaque niveau d’environnement indiquent que dans les environnements terrestres, les UGV ont été évalués significativement plus bas pour la difficulté perçue de la tâche que les UAV [latex]t = 4.78, p < .001[/latex], alors que pour les environnements aériens, c’est le contraire qui est vrai, les UAV étant nettement moins bien notés pour la difficulté perçue de la tâche [latex]t = −5.41, p < .001[/latex]. Cependant, dans les environnements aquatiques, il n’y avait aucune différence significative entre les UAV et les UGV – les deux étaient considérés comme tout aussi difficiles à explorer.
En résumé, les ANOVA suivent la même logique que les tests statistiques que nous avons étudiés tout au long de ce chapitre, basés sur le rapport de la variance expliquée à la variance non expliquée. Cette logique peut être étendue à des analyses plus complexes, par exemple lorsque vous avez trois variables indépendantes (ANOVA à 3 facteurs), ou un plan expérimental à mesures répétées (ANOVA à mesures répétées), ou un plan combinant à la fois des variables à mesures répétées et entre-groupes (analyse de variance mixte). Les calculs pour ces analyses sont légèrement plus complexes, mais ils reposent tous sur les principes fondamentaux du modèle linéaire général. Ainsi, si vous avez une compréhension approfondie du contenu de ce chapitre, vous serez bien préparé(e) à effectuer des analyses statistiques avancées dans le futur.
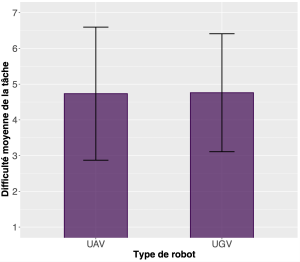
Figure 6-18 : Interaction à deux facteurs entre l’environnement de tâche et le type de robot
6.8 Résumé du chapitre
Dans ce chapitre, nous avons abordé de nombreux outils mathématiques essentiels pour les roboticiens modernes. Bien que la plupart de ces outils vous soient familiers, nous avons mis l’accent sur la façon dont nous les utilisons dans le domaine de la robotique. De la géométrie aux calculs matriciels en passant par les quaternions et les statistiques d’inférence, ce chapitre sert de référence que vous pourrez consulter tout au long de votre lecture du reste du livre.
6.10 Lectures supplémentaires
Bien que ce chapitre ait présenté les bases de la théorie de l’algèbre linéaire, il est important de connaître certaines limitations pratiques avant de résoudre un problème numérique. Par exemple, même si le déterminant d’une matrice carrée n’est pas nul, il peut ne pas être conseillé de l’inverser pour résoudre un système d’équations linéaires. C’est à ce moment qu’il est important de prendre en compte le conditionnement d’une matrice, qui est quantifiée par le numéro de condition, et qui ne doit pas être proche de 1. Si tel est le cas, les approximations numériques effectuées lors du calcul seront amplifiées, entraînant ainsi des erreurs significatives dans la solution obtenue. De plus, lors de la résolution d’un système d’équations numériques, l’inversion (et l’inversion généralisée) d’une matrice ne possède généralement qu’une valeur théorique, car des algorithmes tels que la décomposition LU, la procédure d’orthogonalisation de Gram-Schmidt et les réflexions de Householder sont utilisés afin d’éviter les erreurs numériques. Pour plus d’informations, vous pouvez vous référer à un manuel d’analyse numérique (Gilat and Subramaniam, 2008; Kong et al., 2020).
Les statistiques abordées dans ce chapitre ne constituent qu’un point de départ pour de nombreuses autres techniques d’analyse de données expérimentales. Si vous souhaitez approfondir vos connaissances sur la théorie des différentes méthodes statistiques, vous pouvez lire Découvrir des statistiques à l’aide de R par Field et al. (2012), également disponible en ligne.
RÉFÉRENCES
Ben-Israel, A., & Greville, T. N. (2003). Generalized inverses: Theory and applications (Vol. 15). Springer Science & Business Media. https://www.maths.ed.ac.uk/~v1ranick/papers/bengrev.pdf
Bender, R., & Lange, S. (2001). Adjusting for multiple testing-when and how? Journal of Clinical Epidemiology, 54(4), 343–349. https://doi.org/10.1016/S0895-4356(00)00314-0
Field, A. P., Miles, J., & Field, Z. C. (2012). http://dx.doi.org/10.1111/insr.12011_21
Discovering statistics using R. SAGE Publications. Gilat, A., & Subramaniam, V. (2008). Numerical methods for engineers and scientists: An introduction with applications using MATLAB. Wiley. https://dl.icdst.org/pdfs/files3/c7cb214eb62807e955167bf60309f95b.pdf
Hassenpflug, W. (1995). Matrix tensor notation part ii. skew and curved coordinates. Computers & Mathematics with Applications, 29(11), 1–103. https://doi.org/10.1016/0898-1221(95)00050-9
Jones, E. M., & Fjeld, P. (2006). Gimbal angles, gimbal lock and a fourth gimbal for Christmas. Apollo Lunar Surface Journal. http://history.nasa.gov/alsj/gimbals.html
Kong, Q., Siauw, T., & Bayen, A. (2020). Python programming and numerical methods: A guide for engineers and scientists. Academic Press. https://pythonnumericalmethods.berkeley.edu/notebooks/Index.html
Liste des tableaux
Tableau 6-1 : Notations de probabilité courantes
Tableau 6-2 : Notations des paramètres communs pour les échantillons par rapport aux populations
Tableau 6-3 : Exemple de données de robots par professeur
Tableau 6-4 : Erreurs de type I et II
Tableau 6-5 : Test t des groupes indépendants
Tableau 6-6 : Moyenne et SD pour la difficulté perçue de la tâche dans chaque environnement de tâche
Tableau 6-7 : Résultats du test F Omnibus pour l’ANOVA à un facteur
Tableau 6-8 : Comparaisons par paires post-hoc pour chaque environnement de tâche sans correction
Tableau 6-9 : Moyennes et SD pour l’environnement de tâche et le type de robot
Tableau 6-10 : Résultats du test F Omnibus pour l’ANOVA à deux facteurs
Tableau 6-11 : Comparaisons par paires post-hoc pour l’ANOVA à deux facteurs sans correction
Liste des figures
Figure 6-1 : Différents systèmes de coordonnées dans l’espace 3D
Figure 6-2 : Vecteurs planaires et leurs composants dans différents cadres
Figure 6-3 : Vecteurs unitaires définissant un repère cartésien
Figure 6-5 : Rotation planaire et coordonnées polaires.
Figure 6-6 : Représentation vectorielle de la rotation plane à l’aide de l’axe imaginaire i.
Figure 6-7 : Diagramme de Venn des nombres pairs et des nombres supérieurs à 3
Figure 6-8 : La distribution normale
Figure 6-9 : La dérivée d’une fonction donne la pente instantanée de cette fonction.
Figure 6-10 : Distribution de fréquence du nombre de robots par laboratoire
Figure 6-12 : Deux courbes en cloche se chevauchant à partir d’échantillons différents
Figure 6-13 : p-valeurs par rapport à la distribution normale
Figure 6-15 : Comparaison des distributions t et z
Figure 6-16 : Fonction de densité de probabilité pour chaque algorithme
Figure 6-17 : Interaction à deux facteurs entre l’environnement de tâche et le type de robot
Figure 6-18 : Interaction à deux facteurs entre l’environnement de tâche et le type de robot
- https://mathworld.wolfram.com/CoordinateSystem.html ↵
- se référer à https://mathworld.wolfram.com/SphericalCoordinates.html ↵
- https://www.merriam-webster.com/dictionary/vector ↵
- pour plus d’informations sur les tenseurs et leur classification : https://mathworld.wolfram.com/Tensor.html ↵
- longueur, toujours positive ↵
- avec une magnitude de 1 ↵
- Le composant (i, j) est le composant sur la i e rangée et la jème colonne. ↵
- même nombre de lignes et de colonnes ↵
- La matrice des cofacteurs ne sera pas introduite ici par souci de brièveté, mais sa définition peut être trouvée dans n’importe quel manuel d’algèbre linéaire. ↵
- https://www.ztable.net/ ↵
- https://github.com/Foundations-of-Robotics/Stats-examples ↵

