Comment manipuler? Cinématique, dynamique et architecture des bras robotiques

Reconnaitre l’architecture et les mobilités d’un bras robotisé;
Résoudre le problème de cinématique directe et inverse des manipulateurs sériels et parallèles;
Obtenir le jacobien reliant les vitesses des articulations à l’organe effecteur;
Analyser le jacobien pour obtenir les différentes singularités et comprendre leur signification physique;
Obtenir les équations définissant la dynamique d’un robot manipulateur.

qq

10.2 Introduction

Les manipulateurs ne sont pas fondamentalement différents des autres systèmes robotiques en ce qui concerne leur cinématique et leur dynamique. Ils sont définis par leur nombre de degrés de liberté (DDL) et leur architecture, qui sont critiques pour l’application envisagée. Ce chapitre vous fournira un aperçu de la cinématique des bras de robot, y compris les problèmes de la cinématique directe et de la cinématique inverse, les différents types de et comment les trouver. Comme la cinématique ne suffit pas à elle seule pour un contrôle avancé, vous devrez ´également comprendre la dynamique d’un manipulateur robotique; nous allons aborder ce sujet brièvement.

Une perspective industrielle

Entretien avec Juxi Leitner, co-fondateur de LYRO Robotics.

Ma formation est en informatique. J’ai commencé à programmer des ordinateurs quand j’étais jeune (il n’y avait pas grand-chose d’autre à faire dans ma toute petite ville natale au milieu des Alpes).

Quand j’avais environ 15 ou 16 ans, j’ai réalisé que la plupart de mon code vivait dans un ordinateur et n’interagissait pas vraiment ou ne changeait pas les choses dans le monde réel. J’ai commencé à m’intéresser de plus en plus à la robotique et à m’inspirer des films de l’époque, comme The Matrix, I robot et Minority Report (je voulais construire ces robots-araignées!) J’ai alors commencé à chercher des moyens d’en savoir plus à ce sujet et je me suis inscrit à un diplôme universitaire commun en robotique spatiale.

Pendant plus d’une décennie, j’ai effectué des recherches sur la robotique dans des milieux universitaires, avant d’essayer de transférer la technologie dans des applications du monde réel avec notre jeune entreprise, LYRO Robotics.

Au départ, je m’intéressais aux essaims de robots et à la coordination multi-robots (pour l’exploration spatiale en particulier), mais j’ai eu de la chance et j’ai pu participer à un programme d’été à Lisbonne pour travailler avec l’iCub European Humanoid alors en plein développement. J’ai été fasciné par la facilité avec laquelle certaines tâches nous sont faciles à effectuer, et par la difficulté que les systèmes robotiques ont pour effectuer ces mêmes tâches, comme la détection du monde autour du robot (même comment décider sur quoi focaliser vos « yeux »/caméras) ou à quel point il est difficile de ramasser un simple objet sur une table devant le robot.

Pour moi, cela a été une expérience qui m’a ouvert les yeux et j’ai été enthousiasmé par le sujet de l’incarnation et par la manière d’intégrer la perception et l’intelligence à la présence physique du système robotique, pour permettre une interaction physique avec le monde! Et plus de 17 ans plus tard, je trouve toujours cela encore très fascinant 🙂

Un autre moment décisif pour moi a été de participer et finalement de gagner le prix Amazon Robotics Challenge en 2017. Les robots industriels ont été conçus pour effectuer des tâches spécifiques, et non pas de sélectionner des objets aléatoires dans un encombrement dynamique. Former l’équipe (nous étions 20) et concevoir le système robotique était vraiment génial. La partie qui consistait à résoudre un problème du monde réel avec une technologie fondamentale que nous avons recherchée pendant des années était particulièrement excitante (et frustrante en même temps).

La victoire a montré que la réflexion sur toutes les options, du matériel au logiciel, est très importante pour concevoir des robots qui fonctionnent. Nous avons donc commencé à chercher des applications dans le monde réel et avons fondé LYRO en 2019 pour apporter des robots sur des marchés actuellement mal desservis pour diverses raisons (les robots étaient trop chers ou incapables d’accomplir leur tâches proprement).

Plusieurs des théories discutées dans ce chapitre sont pertinentes dans le monde réel.

Par exemple, iCub s’est inspiré de la cinématique d’un jeune enfant. En particulier, la main a beaucoup de degrés de liberté, trois à l’épaule, deux au coude et deux au poignet. En outre, la main a aussi neuf degrés de liberté de plus (étant donné qu’elle a cinq doigts). Cela a souligné un problème intéressant pour moi : la cinématique avant est assez simple (si vous avez des mesures correctes), mais la cinématique inverse, comme lorsque j’ai la position d’un objet que je veux saisir, comment déplacer mes différentes articulations, est un problème très difficile et délicat avec des singularités et des non-linéarités partout.

Pendant mon doctorat, nous devions régulièrement réparer les câbles du iCub, car nous rencontrions (ou dépassions) les limites et cassions des choses!

Je travaille dans les applications robotiques de préhension, et l’avènement de l’apprentissage machine il y a 20 ans et de l’apprentissage profond il y a dix ans a clairement eu un grand impact. Cependant, alors que la citation « la préhension est résolue », il n’est toujours pas trivial d’obtenir un bras robotique qui peut ramasser n’importe quel objet aléatoire dans n’importe quelle configuration aléatoire et effectuer une tâche utile avec ce dernier.

Le domaine s’agrandit, c’est une bonne chose, mais il manque de reproductibilité ce qui freine la progression.

D’un autre côté, c’est une période très excitante, car tout le domaine se tourne davantage vers des robots qui exécutent des tâches de manière intelligente plutôt que d’effectuer « simplement » la même action encore et encore.

qq

10.3 Architectures

L’incarnation physique d’un manipulateur robotique (nous utiliserons le terme robot au sens large dans ce chapitre) est une chaîne cinématique composée d’un ensemble de corps rigides, appelés liens, reliés en série par des articulations (anciennement connu sous le nom de paires cinématiques). En d’autres termes, une articulation contraint le mouvement entre deux corps. Il existe deux types d’articulations, à savoir les paires cinématiques inferieures (PCI) et les paires cinématiques supérieures (PCS). Par définition, le premier type implique ”un contact se produisant le long d’une surface commune aux deux corps”. (Angeles, 2014) Vous avez probablement déjà rencontré les deux articulations les plus courantes appartenant à cette catégorie : les articulations rotoïdes (rotation, R) et les articulations prismatiques (translation, P). Bien qu’il existe également quatre autres types de PCI, hélicoïdal (vis, H), cylindrique (C), universel (U), sphérique (S), toutes peuvent être obtenues avec une combinaison d’articulations rotoïdes et prismatiques. Par conséquent, ce chapitre portera presque exclusivement sur ces deux types d’articulation. Alors que la plupart des articulations couramment utilisées dans les robots n’ont qu’un seul degré de liberté (DDL), à savoir les articulations rotoïdes et prismatiques mentionnées ci-dessus, d’autres types d’articulations existent également, telles que les articulations sphériques et cylindriques, avec respectivement trois et deux DDL. Comme nous le verrons dans la sous-section sur les manipulateurs à poignet à axes concourants, les trois dernières articulations rotoïdes de ce type de robot sont équivalentes à une articulation sphérique.

Figure 10‑1 : Kinova Gen3 lite, un manipulateur robotique sériel à 6 DDL

Les architectures des manipulateurs robotiques peuvent être classées en deux grandes catégories : série et parallèle. La première catégorie, la plus courante dans l’industrie manufacturière, comprend les manipulateurs composés de chaînes cinématiques simples et ouvertes. Ils sont connus pour leur portée et leur simplicité. Le Kinova Gen3 lite, illustré dans la figure 10-1, fait partie de cette catégorie avec ses chaînes cinématiques 6R, c’est-à-dire une boucle ouverte de 6 articulations rotoïdes actionnées en série. La deuxième catégorie comprend les manipulateurs parallèles, qui sont basés sur des chaînes cinématiques complexes constituées d’au moins une boucle. Ils sont connus pour leur rigidité structurelle, leur vitesse et leur capacité à soulever une charge utile plus importante par rapport à la masse du robot. Alors que pour le manipulateur sériel, la plupart des actionneurs doivent être déplacés pendant le mouvement du robot, les actionneurs d’un manipulateur parallèle peuvent tous être fixés de manière rigide à la base.

Les manipulateurs peuvent également être classés selon leur mobilité, qui incluent leurs DDL et le type de mouvement qu’ils peuvent générer. Par exemple, l’un des types les plus importants de manipulateurs robotiques est les générateurs de mouvement Schönflies (SMG). Ces robots à4 DDL, capables de trois translations et d’une rotation autour d’un axe de direction fixe (généralement l’axe vertical), sont communément appelés robots SCARA, d’après l’un des premiers SMG et parmi les plus connus, le Selective-Compliance Assembly Robot Arm (SCARA) (bras robotique d’assemblage à conformité sélective), un robot série avec une articulation prismatique et trois articulations rotoïdes (Makino et al, 2007). Ces manipulateurs peuvent disposer d’une architecture sérielle ou parallèle. De nos jours, la plupart des manipulateurs industriels disposent de 5 à 7 DDL, comme le Kinova Gen3 et Gen3 lite.

10.4 Cinématique des manipulateurs sériels

Les manipulateurs sériels sont considérés comme des chaînes cinématiques simples^[1] 6R, c’est-à-dire que chaque lien peut être couplé via une ou deux articulations, à un ou deux liens. Le premier lien est la base et le dernier lien est le « organe effecteur », parfois appelé l’outil. Dans ce qui suit, nous examinerons de plus près la cinématique directe et inverse des manipulateurs sériels.

10.4.1 Cinématique directe

La cinématique est utilisée pour décrire le mouvement d’un robot sans tenir compte de la dynamique, à savoir les forces et les couples provoquant le mouvement. Par conséquent, les problèmes cinématiques sont des problèmes géométriques. Premièrement, nous considérons la cinématique directe (CD), parfois appelée modèle géométrique direct (GD), d’un robot série. Les équations CD sont utilisées pour cartographier les variables des articulations, appelées posture ou configuration du robot, dans la position et l’orientation de l’organe effecteur, à savoir sa pose.

À la fin, vous obtiendrez un système explicite d’équations non linéaires pour calculer [latex]\mathbf{p}=[p_x\quad p_y\quad p_z]^T[/latex], le vecteur tridimensionnel représentant la position cartésienne de l’organe effecteur, ainsi qu’une matrice 3 × 3 d’orientation orthogonale (rotation) Q composée de trois vecteurs unitaires parallèles aux axes X-, Y – et Z– de l’organe effecteur (exprimés dans le référentiel du repère de base). Toutes les deux matrices p et Q peuvent être regroupées en une seule matrice homogène 4 × 4, comme vous le verrez.

10.4.2 Convention Denavit-Hartenberg

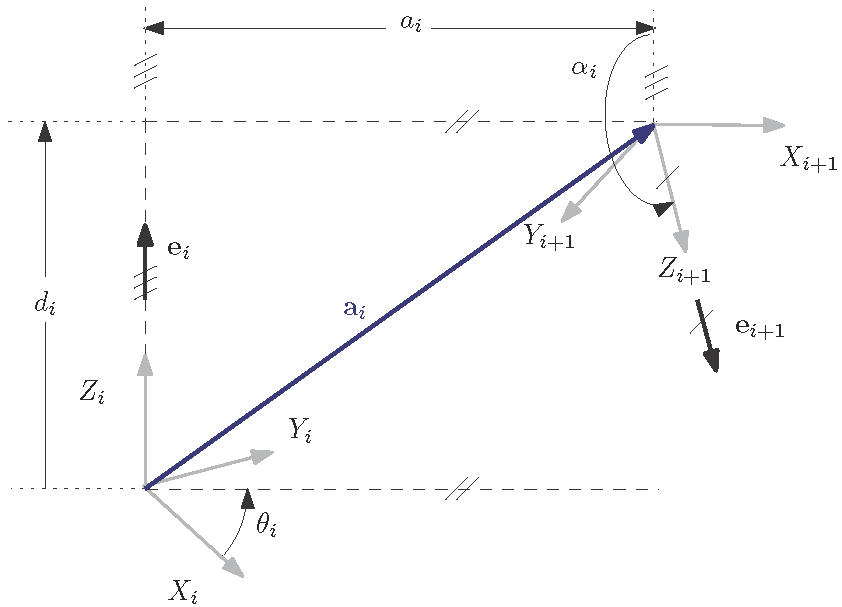
Il est impossible d’aborder le sujet de la cinématique directe des robots série sans évoquer la Convention de Denavit-Hartenberg (DH). C’est un outil puissant qui vous aidera à résoudre de manière systématique la cinématique directe d’un manipulateur sériel. Depuis que cette méthode a été introduite pour la première fois par Hartenberg et Denavit (Hartenberg and Denavit, 1964), quelques variantes ont été proposées. Ici, nous utilisons la notation de Paul, également connue sous le nom de variante distale (Lipkin, 2008). Chaque lien est numéroté de 0 à n, 0 étant la base, tandis que n est le lien n^th, à savoir la bride du robot à laquelle l’organe effecteur est attaché. L’articulation i^th est définie comme celle reliant les liens (i−1)^th et i^th. Alors que la cinématique directe d’un robot être résolue sans utiliser la convention DH (ou toute autre), elle simplifie considérablement le processus et peut-être facilement comprise par d’autres ingénieurs familiarisés avec la notation DH. Attention : les lignes suivantes couvrent plusieurs définitions et formules, mais la procédure devient rapidement facile à utiliser après quelques exemples. Pour chaque lien, un repère cartésien est défini. Deux de ces repères sont représentés dans la figure 10-2. Veuillez noter que les axes (X_i,Y_i,Z_i) sont solidement fixés au lien (i − 1)^th. La convention suivante est utilisée :

Z_iest l’axe de la paire/articulation cinématique i^th.
X_iest la normale commune entre Z₍_i₋₁₎et Z_i. Contrairement à l’axe Z_i, qui n’a pas de direction prescrite, X_iest orienté de Z₍_i₋₁₎vers Z_i. S’ils se croisent, entrainant ainsi une direction indéfinie pour l’axe X_i, la convention est d’utiliser le produit vectoriel des vecteurs unitaires parallèles àZ₍_i₋₁₎et Z_ii_i= k₍_i₋₁₎×k_i. Dans le cas où le premier et le second sont parallèles, X_iest choisi arbitrairement pour compléter le repère cartésien, c’est-à-dire orthogonal à Z₍_i₋₁₎et Z_i.
Avec la règle de la main droite^[2], Y_iest défini.

Avec ces repères et leurs axes respectifs, quatre paramètres sont définis pour i = 1…n : θ_i, α_i, d_i, a_i, i = 1…n, étant respectivement l’angle d’articulation, la torsion de lien, le décalage de lien et la longueur du lien. Ils sont définis ci-dessous :

a_i représente la distance^[3] entre Z_iet Z₍_i₊₁₎sur X₍_i₊₁₎.
d_i représente la coordonnée^[4], sur Z_i, depuis l’origine du repère i^th à l’intersection avec X(i+1).
α_iest l’angle entre Z_iet Z₍_i₊₁₎, mesuré par rapport à la direction positive de X₍_i₊₁₎.
θ_i est l’angle entre X_iet X₍_i₊₁₎, mesuré par rapport à la direction positive de Z_i.

Une matrice de transformation homogène, comme définie au Chapitre 6 (Section 6.4.4) est obtenue à partir de ces paramètres, c’est-à-dire:

[latex]\mathbf{H}_{i-1}^i \equiv \begin{bmatrix} \cos\theta_i & -\sin\theta_i\cos\alpha_i & \sin\theta_i\sin\alpha_i & a_i\cos\theta_i\\ \sin\theta_i & \cos\theta_i\cos\theta_i & -\cos\theta_i\sin\alpha_i & a_i\sin\theta_i\\ 0 & \sin\alpha_i & \cos\alpha_i & d_i\\ 0 & 0 & 0 & 1 \end{bmatrix} \label{e:DH_transformation}[/latex]

(10.1)

Où l’indice désigne le repère de référence dans lequel les coordonnées sont données, (i−1) dans cette notation. Il peut également être séparé dans la matrice de rotation Qⁱ_i₋₁et le vecteur déplacement a_i, c’est-à-dire:

[latex]\begin{equation} \mathbf{H}_{i-1}^i=\begin{bmatrix} \mathbf{Q}_{i-1}^i & \mathbf{a}_{i-1}^i\\ \mathbf{0}^T & 1 \end{bmatrix} \end{equation}[/latex]

(10.2)

Figure 10‑2 : Représentation des repères dans la convention DH

L’orientation et la position de l’organe effecteur sont ainsi obtenues en multipliant les matrices de transformation individuelles associées aux paramètres DH, nous donnant :

[latex]\begin{align} \mathbf{Q}&=\mathbf{Q}_0^1\mathbf{Q}_1^2\mathbf{Q}_2^3\mathbf{Q}_3^4\mathbf{Q}_4^5\mathbf{Q}_5^6\label{e:orientation}\\ \end{align}[/latex]

(10.3a)

[latex]\begin{align}\mathbf{p}&=\sum^6_{i=1} \mathbf{a}_0^i\quad\textrm{où}\label{e:position}\\ \end{align}[/latex]

(10.3b)

[latex]\begin{align} \mathbf{p}&=\mathbf{a}_0^1+\mathbf{Q}_0^1\mathbf{a}_1^2+\mathbf{Q}_0^1\mathbf{Q}_1^2\mathbf{a}_2^3+\mathbf{Q}_0^1\mathbf{Q}_1^2\mathbf{Q}_2^3\mathbf{a}_3^4+\mathbf{Q}_0^1\mathbf{Q}_1^2\mathbf{Q}_2^3\mathbf{Q}_3^4\mathbf{a}_4^5+\mathbf{Q}_0^1\mathbf{Q}_1^2\mathbf{Q}_2^3\mathbf{Q}_3^4\mathbf{Q}_4^5\mathbf{a}_5^6\\\label{e:position2}\\ \end{align}[/latex]

(10.3c)

[latex]\begin{align} \mathbf{H}&=\begin{bmatrix} \mathbf{Q} & \mathbf{p}\\ \mathbf{0}^T & 1 \end{bmatrix}= \mathbf{H}_0^1\mathbf{H}_1^2\mathbf{H}_2^3\mathbf{H}_3^4\mathbf{H}_4^5\mathbf{H}_5^6 \end{align}[/latex]

(10.3d)

Où H est la matrice de transformation homogène représentant à la fois la position et l’orientation de l’organe effecteur. Par souci de concision, dans la suite, si seul un indice est donné pour une matrice de rotation/transformation, il est donné dans le repère précédent.

Pour une articulation avec un seul DDL, telle qu’une articulation rotoïde ou prismatique, un seul des quatre paramètres (a_i, d_i, θ_i, α_i) est une variable, les autres sont des constantes. Comme mentionné précédemment, une matrice de transformation homogène est caractérisée par six paramètres dans l’espace 3D. Ici, ce nombre est réduit à quatre puisque, avec la convention DH, la localisation de l’origine du repère i n’est pas choisie arbitrairement. En effet, nous avons deux contraintes pour l’axe X de chaque repère suivant : (1) X_idoit être normal à Z_iet (2) il doit également l’intersecter. Le repère est rigidement attaché au lien i, mais il n’est pas nécessairement situé à la fin du lien, comme on pourrait s’y attendre. En fait, il peut se situer en dehors du lien lui-même. Le nombre réduit de paramètres définissant les matrices de transformation est l’un des principaux atouts de la notation DH.

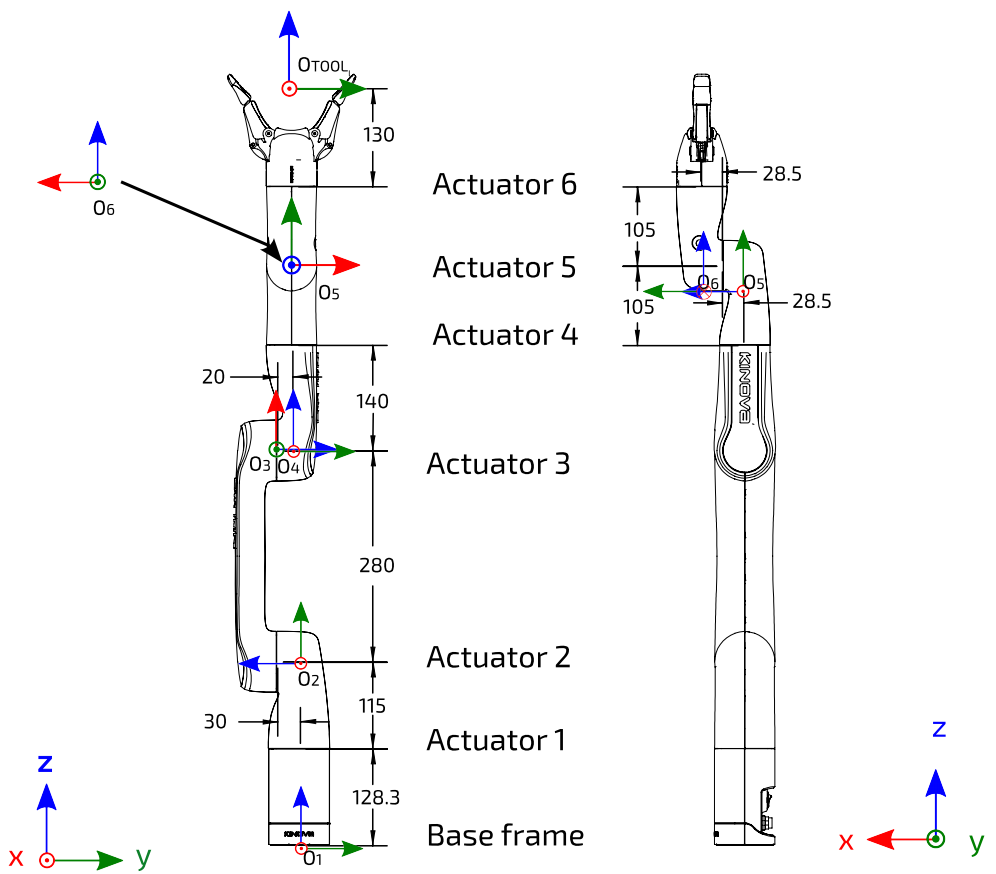
Figure 10‑3 : Les repères DH pour chaque articulation du Kinova Gen3 lite (extrait du manuel d’utilisation du manipulateur)

Les repères DH appliqués au Kinova Gen3 lite sont illustrés à la figure 10-3, et les paramètres DH correspondants sont détaillés dans le tableau 10-1. Puisque les six articulations du Gen3 lite sont rotoïdes, toutes les θ_i sont des inconnues. Au chapitre 18, plus précisément dans le projet 3, vous devrez trouver les paramètres DH d’une version 3-DDL de ce manipulateur^[5], ainsi que de calculer sa cinématique directe et inverse.

Tableau 10‑1 : Paramètres DH du Kinova Gen3 lite

i	1	2	3	4	5	6
a_i	0	a₂	0	0	0	0
d_i	d₁	d₂	d₃	d₄	d₅	d₆
α_i	π/2	π	π/2	π/2	π/2	0

10.4.3 Cinématique inverse

Comme mentionné au début de ce chapitre, la résolution de la cinématique inverse permet à l’ingénieur d’obtenir l’ensemble des coordonnées des articulations, à savoir la posture du robot, à partir d’une position et d’une orientation de l’organe effecteur, à savoir la pose. Contrairement à la cinématique directe, qui ne donne qu’une seule pose organe effecteur à partir d’un ensemble de coordonnées des articulations, il peut y avoir plus d’une solution à la cinématique inverse, c’est-à-dire plus d’une posture qui correspond à une position/orientation de l’organe effecteur. Cependant, une solution analytique (symbolique et exacte) à la cinématique inverse n’est pas nécessairement toujours obtenue; cela dépend de l’architecture du manipulateur robotique. Dans certains cas, une approche numérique est préférable. Les approches numériques conviennent également davantage aux simulateurs compatibles avec diverses architectures de manipulateurs. Les différentes solutions à la cinématique inverse sont appelées types de configuration. Généralement, lorsqu’il est en mouvement, un manipulateur gardera le même type de configuration, car alterner d’un type de configuration à l’autre nécessite de fortes variations d’angle d’articulation pour obtenir, à la fin, les mêmes coordonnées d’organe effecteur. Changer de configuration peut également créer un risque de passer par une singularité, dont nous parlerons plus tard. Le contrôleur des manipulateurs disponibles dans le commerce tient compte de ces éléments lors du calcul des positions et des vitesses des articulations.

Pour résoudre symboliquement la cinématique inverse pour les équations explicites, nous commençons avec les mêmes équations utilisées ci-dessus, c’est-à-dire celles définies par la matrice de transformation homogène 4 × 4, c’est-à-dire H. Comme la dernière ligne est toujours [0 0 0 1], nous avons donc 12 équations non linéaires, mais seulement 6 équations inconnues dans le cas d’un manipulateur spatial^[6] non redondant. Bien entendu, si le robot a des articulations supplémentaires, par exemple pour atteindre une cible dans un espace de travail encombré (ex. opérations de soudage), le nombre de solutions potentielles augmente.

Dans ce chapitre, seuls les manipulateurs non redondants seront traités.

Comme mentionné précédemment, alors que nous disposons de 9 équations pour l’orientation de l’organe effecteur, seules 3 sont indépendantes, ce qui nous donne un système de 6 équations avec 6 inconnues (3 pour l’orientation, 3 pour la position). La résolution de la cinématique inverse pour un manipulateur sériel générale est donc un problème mathématique difficile compte tenu de la non-linéarité des équations. Cependant, vous constaterez que la plupart des manipulateurs disponibles dans le commerce appartiennent à la catégorie spéciale à poignet à axes concourants, simplifiant grandement le problème, comme nous le montrerons ci-dessous.

10.4.3.1 Manipulateurs à poignet à axes concourants

L’architecture du manipulateur sériel découplé (poignet à axes concourants) permet de séparer le problème d’orientation du problème de position. Par conséquent, nous obtenons des

équations explicites, évitant ainsi le besoin d’une méthode numérique pour résoudre la cinématique inverse. Le problème est donc divisé en cinématique en position inverse et cinématique d’orientation inverse. Par définition, les axes des trois dernières articulations des manipulateurs découplés se croisent. Ce point est connu sous le nom de centre du poignet. En revenant aux paramètres DH, cela signifie que a₄= a₅= a₆= 0. Cela signifie également que les trois derniers repères DH partagent la même origine. Les coordonnées de ce dernier sont données par le vecteur p_w dans le repère 0, c’est-à-dire :

[latex]\begin{equation} \mathbf{p}_w = \mathbf{a}_1+\mathbf{Q}_1\mathbf{a}_2+\mathbf{Q}_1\mathbf{Q}_2\mathbf{a}_3+\mathbf{Q}_1\mathbf{Q}_2\mathbf{Q}_3\mathbf{a}_4 \label{e:p_w123} \end{equation}[/latex]

(10.4)

Puisque a₄= 0, a₄n’est pas une fonction de θ₄, comme l’équation de p_w ci-dessus. Avec eq. (10.3b), nous pouvons réécrire l’équation ci-dessus comme:

[latex]\begin{equation} \mathbf{p}_w = \mathbf{p} -\mathbf{Q}_1\mathbf{Q}_2\mathbf{Q}_3\mathbf{Q}_4\mathbf{a}_5-\mathbf{Q}_1\mathbf{Q}_2\mathbf{Q}_3\mathbf{Q}_4\mathbf{Q}_5\mathbf{a}_6 \end{equation}[/latex]

(10.5)

Ce qui peut-être simplifié, sachant qu’avec un poignet découplé, a₅= 0, comme:

[latex]\begin{equation} \mathbf{p}_w = \mathbf{p} - \mathbf{Q}\mathbf{Q}_6^T\mathbf{a}_6 \label{e:p_w} \end{equation}[/latex]

(10.6)

Cette équation est uniquement fonction des paramètres DH constants et de la position cible et des coordonnées d’orientation de l’organe effecteur dans le cas d’une cinématique inverse. Par conséquent, l’emplacement du poignet, p_w, peut-être calculé dans le repère de base sans les coordonnées de l’articulation, en dissociant la position de l’orientation.

En bref, nous résolvons le problème de position en calculant d’abord l’emplacement du poignet avec eq. (10.6), puis en isolant les trois premières coordonnées des articulations dans eq. (10.4), qui est un problème de 3 DDL plus simple avec 3 équations et 3 inconnues.

10.4.3.2 Exemple : Manipulateur sériel à 3 DDL

À titre d’exemple, nous pouvons résoudre le problème de position inverse à 3 DDL pour un` manipulateur sériel générique avec trois articulations rotoïdes. Il convient de noter que la procédure ci-dessous peut-être légèrement adaptée dans certains cas particuliers (paramètres DH nuls, certains angles, division par zéro, etc.). Il faut d’abord réécrire eq. (10.4) :

[latex]\begin{equation} \mathbf{Q}_1^T(\mathbf{p}_w-\mathbf{a}_1)= \mathbf{a}_2+\mathbf{Q}_2\mathbf{a}_3+\mathbf{Q}_2\mathbf{Q}_3\mathbf{a}_4 \end{equation}[/latex]

(10.7)

Cela peut-être accompli parce que les matrices de rotation sont orthogonales, donc Q⁻_i¹= Q^T_i . En développant l’équation ci-dessus en termes de ses composantes, nous avons :

[latex]\begin{align} A\cos\theta_2+B\sin\theta_2 &= x_w\cos\theta_1+y_w\sin\theta_1-a_1\\ \end{align}[/latex]

(10.8a)

[latex]\begin{align} A\sin\theta_2-B\cos\theta_2 &= \cos\alpha_1(y_w\cos\theta_1-x_w\sin\theta_1)+(z_w-b_1)\sin\alpha_1\\ \end{align}[/latex]

(10.8b)

[latex]\begin{align} C &= \sin\alpha_1(x_w\sin\theta_1-y_w\cos\theta_1)+(z_w-b_1)\cos\alpha_1 \end{align}[/latex]

(10.8c)

Avec;

[latex]\begin{align} A =& a_2+a_3\cos\theta_3+b_4\sin\alpha_3\sin\theta_3\\ \end{align} \label{e:positioning1}[/latex]

(10.8d)

[latex]\begin{align} B =& -a_3\cos\alpha_2\sin\theta_3+b_3\sin\alpha_2+b_4\cos\alpha_2\sin\alpha_3\cos\theta_3+b_4\sin\alpha_2\cos\alpha_3\\ \end{align} \label{e:positioning1-1}[/latex]

(10.8e)

[latex]\begin{align} C =& b_2+a_3\sin\alpha_2\sin\theta_3+b_3\cos\alpha_2-b_4\sin\alpha_2\sin\alpha_3\cos\theta_3+b_4\cos\alpha_2\cos\alpha_3 \end{align} \label{e:positioning1-1f}[/latex]

(10.8f)

Nous pouvons constater que le côté droit de eqs. (10.8(a-c)) est uniquement fonction de θ₁, la position du poignet et des paramètres DH. Comme :

[latex]\begin{align} D =& x_w\cos\theta_1+y_w\sin\theta_1-a_1\\ \end{align}[/latex]

(10.9)

[latex]\begin{align} E =& \cos\alpha_1(y_w\cos\theta_1-x_w\sin\theta_1)+(z_w-b_1)\sin\alpha_1 \end{align}[/latex]

(10.10)

Nous pouvons convertir eqs. (10.8(a-b)) sous forme matricielle, c’est-à-dire

[latex]\begin{equation} \begin{bmatrix} A & -B\\ -B & A \end{bmatrix} \begin{bmatrix} \cos\theta_2\\ \sin\theta_2 \end{bmatrix}= \begin{bmatrix} D\\E \end{bmatrix} \end{equation}[/latex]

(10.11)

Nous sommes maintenant capables de calculer des fonctions explicites de sinθ₂et cosθ₂:

[latex]\begin{align} \cos\theta_2 = (AD-BE)/(A^2+B^2)\\ \end{align}[/latex]

(10.12)

[latex]\begin{align} \sin\theta_2 = (BD-AE)/(A^2+B^2) \end{align}[/latex]

(10.13)

Qui mène à :

[latex]\begin{equation} \theta_2 = \textrm{arctan2}(\sin\theta_2,\cos\theta_2)\label{e:th2} \end{equation}[/latex]

(10.14)

Évidemment, θ₂ne peut pas être calculé immédiatement, car les valeurs des deux autres angles des articulations sont nécessaires. Dans ce but, nous devons faire disparaître θ₂. Pour ce faire, nous devons calculer la somme des carrés de chaque côté de eqs. (10.8(a-c). Puisque nous connaissons sin²θ₂cos²θ₂= 1, nous obtenons :

[latex]\begin{equation} A^2+B^2+C^2 = x_w^2+y^2+(z_w-b_1)^2+a_1^2-2a_1x_w\cos\theta_1-2a_1y_w\sin\theta_1\label{e:positioning2} \end{equation}[/latex]

(10.15)

Le côté gauche de l’équation ci-dessus n’est qu’une fonction des paramètres DH et θ₃, tandis que le côté droit ne dépend que des paramètres DH et θ₁. En outre, eq. (10.15) est linéaire dans sinθ₁, sinθ₃, cosθ₁et cosθ₃. En calculant la somme des carrés de eqs. (10.8(a-b)) à la place, nous aurions quand même éliminé θ₂, mais l’équation résultante n’aurait pas été linéaire dans les termes mentionnés ci-dessus, ce qui est nécessaire pour les étapes suivantes. Par conséquent, eq. (10.15) est réécrite comme :

[latex]\begin{equation} F_1\cos\theta_1+G_1\sin\theta_1+H_1\cos\theta_3+I_1\sin\theta_3+J_1=0 \label{e:positioning3} \end{equation}[/latex]

(10.16)

Où F₁, G₁, H₁, I₁et J₁ne sont fonction que des paramètres DH et de la position du poignet, toutes ces valeurs étant connues à ce stade. Ensuite, eq. (10.8c) est réécrite sous une forme similaire, c’est-à-dire :

[latex]\begin{equation} F_2\cos\theta_1+G_2\sin\theta_1+H_2\cos\theta_3+I_2\sin\theta_3+J_2=0 \label{e:positioning4} \end{equation}[/latex]

(10.17)

De nouveau, F₂, G₂, H₂, I₂et J₂ne sont fonction que des paramètres DH et de la position du poignet. Ayant deux équations linéaires et quatre inconnues, la prochaine étape consiste à obtenir des expressions explicites de cosθ₁et sinθ₁, comme nous l’avons fait avec θ₂. Ainsi, nous obtenons:

[latex]\begin{align} \cos\theta_1 =& \frac{-G_2(H_1\cos\theta_3+I_1\sin\theta_3+J_1)+G_1(H_2\cos\theta_3+I_2\sin\theta_3+J_2)}{F_1G_2-F_2G_1}\\ \end{align}[/latex]

(10.18)

[latex]\begin{align} \sin\theta_1 =& \frac{F_2(H_1\cos\theta_3+I_1\sin\theta_3+J_1)-F_1(H_2\cos\theta_3+I_2\sin\theta_3+J_2)}{F_1G_2-F_2G_1}\\ \end{align}[/latex]

(10.19)

[latex]\begin{align} \theta_1=& \textrm{arctan2}(\sin\theta_1,\cos\theta_1)\label{e:th1}\end{align}[/latex]

(10.20)

Enfin, nous éliminons θ₁en calculant la somme de sin²θ₁et cos²θ₁, ce qui se traduit par :

[latex]\begin{equation} K\cos^2\theta_3+L\sin^2\theta_3+M\cos\theta_3\sin\theta_3+N\cos\theta_3+P\sin\theta_3+Q=0 \label{e:nonlin_unii} \end{equation}[/latex]

(10.21)

Où les coefficients devant les fonctions trigonométriques de θ₃sont fonction de F_i, G_i, H_i, I_iet J₂i, pour i = 1,2, qui sont à leur tour fonction des paramètres DH et de la position du poignet. Nous avons donc une équation non linéaire à coefficients connus où la seule inconnue est θ₃. Pour résoudre cette équation implicite, nous utilisons une identité bien connue dans le domaine de la cinématique, la substitution de Weierstrass (appelée aussi substitution demi-angle tangent) :

[latex]\begin{equation} \cos\theta_3\equiv\frac{1-T_3^2}{1+T_3^2},\quad \sin\theta_3\equiv\frac{2T_3}{1+T_3^2},\quad T_3=\tan(\theta_3/2) \end{equation}[/latex]

(10.22)

Cette substitution permet de réécrire l’équation eq. (10.21) comme une équation de degré quatre dans T₃:

[latex]\begin{equation} RT_3^4+ST_3^4+UT_3^2+VT_3+W=0 \end{equation}[/latex]

(10.23)

Les quatre valeurs possibles pour T₃sont ainsi obtenues en calculant les racines de l’équation ci-dessus. Ces valeurs sont ensuite utilisées pour calculer les solutions pour θ₃avec :

[latex]\begin{equation} \theta_3=2\arctan T_3 \end{equation}[/latex]

(10.24)

Les valeurs des coordonnées des articulations restantes sont ensuite calculées avec d’abord eq. (10.20) et ensuite eq. (10.14) pour θ₁et θ₂respectivement. Par conséquent, nous avons résolu le problème de position inverse pour un manipulateur sériel à3 DDL, en obtenant quatre ensembles de coordonnées des articulations. Remplacer les articulations rotoïdes par des articulations prismatiques permet de simplifier le problème, car deux articulations prismatiques (et une rotoïde) permettent un maximum de deux solutions au problème de position inverse et trois articulations prismatiques permettent une seule solution au problème de position inverse. La position du poignet est maintenant connue, la prochaine étape consiste à trouver les solutions pour les trois articulations restantes.

10.4.3.3 Poignée sphérique

Les trois premières matrices de rotation Q₁, Q₂, Q₃sont maintenant entièrement connues, l’étape suivante consiste à calculer les solutions pour les trois dernières matrices de transformation, qui sont fonction des trois dernières coordonnées de l’articulation. Tout d’abord, nous nous rappelons de eq. (10.3a) et la réécrivons avec tout ce qui est connu à droite, c’est-à-dire :

[latex]\begin{align} \mathbf{Q}_4\mathbf{Q}_5\mathbf{Q}_6=&\mathbf{R}\label{e:Q4Q5Q6}\\ \end{align}[/latex]

(10.25a)

[latex]\begin{align} \mathbf{R}=\mathbf{Q}_3^T\mathbf{Q}_2^T\mathbf{Q}_1^T\mathbf{Q}_d=&\begin{bmatrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{bmatrix} \end{align}[/latex]

(10.25b)

Maintenant, vous devez vous rappeler que selon la notation DH, l’angle entre les axes Z₅et Z₆est α₅. Ces deux axes sont définis par les vecteurs unitaires e₅et e₆. Donc, d’après le produit scalaire, nous avons :

[latex]\begin{equation} \mathbf{e}_5\cdot\mathbf{e}_6=\cos\alpha_5 \end{equation}[/latex]

(10.26)

Nous devons exprimer ces deux vecteurs dans un seul repère référentiel. Le repère DH 4 est choisi, car il simplifie les équations. Dans ce repère, e₅est simplement la dernière colonne de Q₄. Et e₆est la dernière colonne de Q₄Q₅. Pour éviter d’introduire plus d’une inconnue dans l’équation, nous utilisons le fait que:

[latex]\begin{equation} \mathbf{Q}_4\mathbf{Q}_5=\mathbf{R}\mathbf{Q}_6^T\label{e:Q4Q5} \end{equation}[/latex]

(10.27)

Nous obtenons ainsi une équation où θ₄est la seule inconnue :

[latex]\begin{equation} X\cos\theta_4+Y\sin\theta_4=Z \end{equation}[/latex]

(10.28a)

Où :

[latex]\begin{align} X=& -\sin\alpha_4(r_{22}\sin\alpha_6+r_{23}\cos\alpha_6)\\ \end{align}[/latex]

(10.28b)

[latex]\begin{align} Y=& \sin\alpha_4(r_{12}\sin\alpha_6+r_{13}\cos\alpha_6)\\ \end{align}[/latex]

(10.28c)

[latex]\begin{align} Z=& -\cos\alpha_4(r_{32}\sin\alpha_6+r_{33}\cos\alpha_6)+\cos\alpha_5 \end{align}[/latex]

(10.28d)

En utilisant la substitution de Wieirstrass introduite précédemment, l’équation ci-dessus est ensuite transformée en une équation quadratique T₄, où les racines sont calculées et substituées dans θ₄= 2arctanT₄. Pour trouver les valeurs possibles des angles des articulations restants, nous devons revenir à eq. (10.25a). Nous ne gardons que les termes inconnus du côté gauche en prémultipliant par Q^T_4, ce qui nous donne :

[latex]\begin{equation} \mathbf{Q}_5\mathbf{Q}_6=\mathbf{Q}_4^T\mathbf{R} \end{equation}[/latex]

(10.29)

En développant les composantes de l’équation ci-dessus et par simple inspection, on trouve :

[latex]\begin{align} \cos\theta_6=&\frac{r_{12}\sin\alpha_4\sin\theta_4-r_{22}\sin\alpha_4\cos\theta_4+r_{32}\cos\alpha_4-\cos\alpha_5\sin\alpha_6}{\sin\alpha_5\cos\alpha_6}\\\end{align}[/latex]

(10.30a)

[latex]\begin{align} \sin\theta_6=&\frac{r_{11}\sin\alpha_4\sin\theta_4-r_{21}\sin\alpha_4\cos\theta_4+r_{31}\cos\alpha_4}{\sin\alpha_5} \end{align}[/latex]

(10.30b)

Comme précédemment, nous mettons les deux valeurs dans :

[latex]\begin{equation} \theta_6=\textrm{arctan2}(\sin\theta_6,\cos\theta_6) \end{equation}[/latex]

(10.31)

Pour terminer, θ5 se trouve de maniere analogue, mais avec eq. (10.27) au lieu. Par inspection, on trouve:

[latex]\begin{align} \cos\theta_5=&\frac{\cos\alpha_4\cos\alpha_5-r_{32}\sin\alpha_6-r_{33}\cos\alpha_6}{\sin\alpha_4\sin\alpha_5}\\ \end{align}[/latex]

(10.32a)

[latex]\begin{align} \sin\theta_5=&\frac{r_{31}\cos\theta_6-r_{32}\cos\alpha_6\sin\theta_6+r_{33}\sin\alpha_6\cos\theta_6}{\sin\alpha_4}\end{align}[/latex]

(10.32b)

Et on calcule :

[latex]\begin{equation} \theta_5=\textrm{arctan2}(\sin\theta_5,\cos\theta_5) \end{equation}[/latex]

(10.33)

10.4.3.4 Autres manipulateurs

Dans le cas d’un manipulateur sériel sans poignet découplé, il n’existe pas une recette simple pour résoudre la cinématique inverse. Dans certains cas, un solveur numérique est nécessaire pour obtenir les coordonnées des articulations à partir d’un ensemble de coordonnées d’organe effecteur. Dans d’autres cas, des équations explicites peuvent être obtenues, par exemple le Kinova Gen3 lite, mais elles sont propres aux robots avec la même architecture. Cependant, bien que les solutions soient différentes, l’approche pour résoudre la cinématique inverse des manipulateurs qui n’ont pas de poignet à axes concourants est généralement similaire, ce qui réduit le nombre d’inconnues à une seule, pour obtenir les racines d’une équation polynomiale à une variable et calculer les valeurs pour une coordonnée d’articulation, puis en calculant celles des autres articulations par rétrosubstitution, comme nous l’avons fait avec le problème de position inverse du manipulateur à poignet à axes concourants. En effet, cette approche repose principalement sur des identités trigonométriques, par exemple :

sin²θ + cos²θ = 1
sinα sinβ + cosα cosβ = cos(α − β)
cosα cosβ − sinα sinβ = cos(α + β)
sinα cosβ + cosα sinβ = sin(α + β)
sinα cosβ − cosαsinβ = sin(α − β)

Et le concept de l’élimination dyalitique. Ce dernier est utilisé pour réduire le nombre d’inconnues dans un système d’équations non homogènes. La procédure comprend quatre étapes :Réécrire les équations sous forme d’expressions polynomiales où l’une des variables est incluse dans les coefficients; cette variable est appelée la variable éliminée;Il faut autant d’équations que d’inconnues; par conséquent, nous pouvons avoir besoin d’en générer une nouvelle en multipliant l’une des équations par l’une des inconnues par exemple; les équations sont ensuite converties en forme matricielle Ax = 0, où A est une fonction des puissances de la variable éliminée uniquement, et x des autres inconnues; il convient de noter que le dernier élément de x est égal à1;Étant donné qu’une des composantes de´ x n’est pas égale à zéro par définition, A doit être, donc son déterminant doit être égal à zéro; l’étape suivante consiste donc à calculer les racines de de t(A) = 0 pour trouver les valeurs possibles de la variable éliminée;La dernière étape consiste à calculer l’espace nul de A; sachant que la dernière composante doit être égale à1, nous devons simplement mettre à l’échelle le vecteur obtenu pour nous assurer que sa dernière composante est égale à 1.

Exemple : cinématique inverse du Kinova Gen3 lite

Le problème de cinématique inverse du Kinova Gen3 lite peut-être résolu sans recourir à une approche numérique. Compte tenu du nombre d’articulations, un grand ensemble de solutions sont obtenues pour chaque position et orientation possible de l’organe effecteur. La méthodologie pour résoudre la cinématique inverse du manipulateur Kinova Jaco, qui dispose d’une architecture similaire au Gen3 Lite, peut-être trouvée dans la littérature (Gosselin and Liu, 2014). Les solutions réalisables pour une pose choisie arbitrairement de l’organe effecteur sont illustrées à la figure 10-4. Quatre solutions sont présentées ici, mais d’autres solutions auraient pu être obtenues si nous n’avions pas pris en compte les limitations de rotation de l’articulation. Une solution unique peut-être sélectionnée avec un critère particulier, par exemple pour minimiser les rotations de l’articulation, pour minimiser le couple généré par l’actionneur de l’articulation pour soulever une charge utile, pour simplement éviter un obstacle, etc. Alors que le sujet de la solution optimale pour la cinématique inverse ne sera pas abordé dans ce chapitre, de nombreux critères peuvent être trouvés dans la littérature.

10.4.3.5 Approche numérique de la cinématique inverse

La méthode présentée ci-dessus pour trouver la solution symbolique à la cinématique inverse n’est pas nécessairement adaptée à tous les cas d’utilisation pratiques. Par exemple, le calcul des racines d’un polynôme de degré supérieur, ce qui est souvent le cas avec des manipulateurs à plusieurs DDL, peut conduire à des instabilités numériques, donc à des imprécisions sur les valeurs des coordonnées de l’articulation obtenues. L’approche analytique peut également ne pas être assez rapide. Par conséquent, pour éviter les instabilités numériques et trouver la solution symbolique à un cinématique inverse difficile, l’approche numérique est souvent la plus utilisée dans l’industrie. À cet égard, nous introduisons l’algorithme de Newton-Gauss, mais d’autres solutions sont également possibles. Vous devez d’abord utiliser l’orientation et la position de l’organe effecteur pour obtenir un système d’équations non linéaires qui peuvent être écrites comme :

[latex]\begin{equation} \mathbf{f}(\mathbf{x})=\mathbf{0} \end{equation}[/latex]

(10.34)

Laisser la matrice d’orientation souhaitée (définie par exemple par les angles d’Euler) et le vecteur de position souhaité

[latex]\begin{equation} \mathbf{Q}_d=\begin{bmatrix}\mathbf{q}_{d,1} & \mathbf{q}_{d,2} & \mathbf{q}_{d,3} \end{bmatrix},\quad \mathbf{p}_d=\begin{bmatrix} p_{x,d}&p_{y,d}&p_{z,d} \end{bmatrix}^T \end{equation}[/latex]

(10.35)

Et la solution de la cinématique directe définie dans eqs. (10.3a-10.3b). La première peut également être affichée dans un format similaire à Q_det p_d :

[latex]\begin{equation} \mathbf{Q}=\begin{bmatrix}\mathbf{q}_{1} & \mathbf{q}_{2} & \mathbf{q}_{3} \end{bmatrix},\quad \mathbf{p}=\begin{bmatrix} p_x&p_y&p_z \end{bmatrix}^T \end{equation}[/latex]

(10.36)

Pour un manipulateur sériel à6 DDL générique, nous avons donc un système de 12 équations :

[latex]\begin{equation} \mathbf{f}= \begin{bmatrix} \mathbf{q}_{1}-\mathbf{q}_{d,1}\\\mathbf{q}_{2}-\mathbf{q}_{d,2}\\\mathbf{q}_{3}-\mathbf{q}_{d,3}\\ \mathbf{p}-\mathbf{p}_d \end{bmatrix}=\mathbf{0} \end{equation}[/latex]

(10.37)

Où f est un vecteur à12 dimensions, 0 est le vecteur nul de la même dimension et les 6 inconnues sont les coordonnées de l’articulation que nous recherchons. L’algorithme de NewtonGauss peut maintenant être appliqué pour trouver x. À travers ce processus, nous trouverons` une séquence d’approximations de x, définie comme x₁,x₂,…,x_k convergeant vers la solution de la cinématique inverse. L’estimation suivante est définie comme x_k₁. Cet algorithme est basé sur la série de Taylor du premier degré, nous avons donc

[latex]\begin{equation} \mathbf{x}_{k+1}=\mathbf{x}_k+\Delta\mathbf{x}_k \end{equation}[/latex]

(10.38a)

[latex]\begin{equation} \mathbf{f}(\mathbf{x}_{k+1})=\mathbf{f}(\mathbf{x}_{k}+\Delta\mathbf{x}_k)=\mathbf{f}(\mathbf{x}_{k})+\mathbf{J}_f(\mathbf{x}_k)\Delta\mathbf{x}_k=\mathbf{0} \label{e:TS} \end{equation}[/latex]

(10.38b)

(a) Solution #1

(b) Solution #2

(c) Solution #3

(d) Solution #4

Figure 10‑4 : Postures possibles pour la même position d’organe effecteur.

Où J_f(x_k) est le jacobien mathématique de f par rapport à x (Section 6.6.2), c’est-à-dire J_f = ∂f/x), évalué à x_k. Il ne faut pas le confondre avec le(s) jacobien(s) du manipulateur, qui sera/seront introduits plus loin dans ce chapitre. L’ eq. (10.38b) peut-être réécrite comme

[latex]\begin{equation} \mathbf{J}_f(\mathbf{x}_k)\Delta\mathbf{x}_k=-\mathbf{f}(\mathbf{x}_{k}) \end{equation}[/latex]

(10.39)

Pour pouvoir calculer l’incrément suivant ∆x_k pour obtenir ∆x_k₁, il faut donc résoudre le système d’équations surdéterminé, défini par l’équation ci-dessus (J_f étant une matrice verticale, c’est-à-dire plus de lignes que de colonnes). Comme vous n’avez presque jamais de solution exacte pour un système surdéterminé, nous trouverons la solution en minimisant les moindres carrés de l’erreur, connue sous le nom de solution des moindres carrés. Cela est réalisé grâce à l’inverse généralisé de gauche de Moore-Penrose J^L_f (Section 6.3.3), c’est-à-dire:

[latex]\begin{align} \mathbf{J}_f^L=&(\mathbf{J}_f^T\mathbf{J}_f)^{-1}\mathbf{J}_f^T\\ \end{align}[/latex]

(10.40a)

[latex]\begin{align} \Delta\mathbf{x}_k =& -\mathbf{J}_f^L(\mathbf{x}_k)\mathbf{f}(\mathbf{x}_{k}) \end{align}[/latex]

(10.40b)

Vous ne devez pas calculer l’inverse généralisé en soi avec l’équation ci-dessus, puisqu’elle est connue pour générer des problèmes numériques (le nombre conditionnel de J^T_f J_f est, approximativement, le carré de celui de la matrice J_f elle-même, aboutissant à un système mal conditionné (Forsythe, 1970). Au lieu de cela, des algorithmes tels que la décomposition QR et les réflexions Householder sont utilisés, obtenant les mêmes résultats tout en minimisant les problèmes numériques potentiels^[7]. En fonction de la valeur de x₁, l’algorithme convergera vers une solution réalisable (le cas échéant). Pour obtenir au moins certaines des autres solutions potentielles (donc différents types de configuration), plusieurs points de départ x₁doivent être testés.

10.4.4 Jacobien

Les cinématiques directe et inverse dérivées dans les sections précédentes associent les coordonnées des articulations à la position et à l’orientation de l’organe effecteur, et vice-versa. Maintenant, nous prenons en considération la vitesse de l’organe effecteur et les taux de l’articulation. Mathématiquement, la relation entre les deux est le jacobien de la fonction définissant le FKP. Le jacobien est utile pour planifier une trajectoire lisse, pour calculer la valeur clé appliquée par l’organe effecteur, pour déterminer des postures singulières, etc. Pour votre compréhension, une clé est la représentation vectorielle en 6 dimensions des forces et des moments. De même, une torsion est la représentation vectorielle en 6 dimensions des vitesses linéaires et angulaires. Les expressions de torsion et de clé sont, respectivement;

[latex]\begin{equation} \mathbf{t}\equiv \begin{bmatrix} \boldsymbol\omega\\\dot{\mathbf{p}} \end{bmatrix},\quad \mathbf{w}\equiv \begin{bmatrix} \mathbf{n}\\\mathbf{f} \end{bmatrix} \end{equation}[/latex]

(10.41)

Où p˙, ω, f et n sont respectivement la vitesse linéaire tridimensionnelle, la vitesse angulaire, la force et le moment.

Le jacobien pour un manipulateur sériel à lien n est une matrice (6 × n) cartographiant les vitesses n de l’articulation dans le vecteur à 6 dimensions constitué des vitesses linéaires et angulaires de l’organe effecteur, c’est-à-dire la torsion mentionnée ci-dessus. Pour l’instant, supposons uniquement des articulations rotoïdes. Étant donné le vecteur de vitesse angulaire de chaque lien

>[latex]\begin{align} \boldsymbol\omega_0 &= \mathbf{0}\\ \end{align}[/latex]

(10.42a)

[latex]\begin{align} \boldsymbol\omega_1 &= \dot{{q}}_1\mathbf{e}_1\\ \end{align}[/latex]

(10.42b)

[latex]\begin{align} \boldsymbol\omega_2 &= \dot{{q}}_2\mathbf{e}_2+\omega_1\\ \end{align}[/latex]

(10.42c)

[latex]\begin{align} \boldsymbol\omega_3 &= \dot{{q}}_3\mathbf{e}_3+\omega_2\\ \end{align}[/latex]

(10.42d)

[latex]\begin{align} \dots \notag \\ \end{align}[/latex]

(10.42e)

[latex]\begin{align} \boldsymbol\omega_n &= \dot{{q}}_n\mathbf{e}_n+\omega_{(n-1)} \end{align}[/latex]

(10.42f)

Où ˙q_iest la vitesse de l’articulation i ^th, e_i est un vecteur unitaire parallèle à l’axe de l’articulation i^th, à savoir l’axe Z_idu repère DH i^th, et 00 est le vecteur nul tridimensionnel. La vitesse angulaire de l’organe effecteur, ω, est simplement égale àω_n. Comme mentionné précédemment, la position de l’organe effecteur est :

[latex]\begin{equation} \mathbf{p}=\sum^n_{i=1}\mathbf{a}_i \label{e:p} \end{equation}[/latex]

(10.43)

En différenciant l’équation ci-dessus par rapport au temps, on obtient

[latex]\begin{equation} \dot{\mathbf{p}}=\sum^n_{i=1}\dot{\mathbf{a}}_i, \textrm{ where }\dot{\mathbf{a}}_i=\boldsymbol\omega_i\times \mathbf{a}_i, \quad i=1,\dots,n \label{e:pdot} \end{equation}[/latex]

(10.44)

i=1

Substituer eq. (10.42) dans eq. (10.44), et avec quelques manipulations, on obtient :

[latex]\begin{equation} \dot{\mathbf{p}}=\sum^n_{i=1}\dot{q}_i\mathbf{e}_i\times \mathbf{r}_i,\quad \mathbf{r}_i \equiv \sum^n_{j=i}\mathbf{a}_j \end{equation}[/latex]

(10.45)

Où r_iest défini comme le vecteur à partir du repère DH i^th au dernier repère DH attaché à l’organe effecteur. Nous pouvons réécrire les équations précédentes sous une forme matricielle plus compacte :

[latex]\begin{equation} \boldsymbol\omega=\mathbf{A}\dot{\mathbf{q}},\quad \dot{\mathbf{p}}=\mathbf{B}\dot{\mathbf{q}} \end{equation}[/latex]

(10.46)

Avec:

[latex]\begin{equation} \mathbf{A} \equiv \begin{bmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \dots & \mathbf{e}_n \end{bmatrix},\quad \mathbf{B} \equiv \begin{bmatrix} \mathbf{e}_1\times \mathbf{r}_1 & \mathbf{e}_2\times \mathbf{r}_2 & \dots & \mathbf{e}_n\times \mathbf{r}_n \end{bmatrix} \end{equation}[/latex]

(10.47)

[latex]\begin{equation} \mathbf{J}=\begin{bmatrix}\mathbf{A}\\\mathbf{B} \end{bmatrix}=\begin{bmatrix} \mathbf{j}_1&\mathbf{j}_2&\dots&\mathbf{j}_n \end{bmatrix},\quad\mathbf{j}_i=\begin{bmatrix} \mathbf{e}_i\\\mathbf{e}_i\times \mathbf{r}_i \end{bmatrix} \end{equation}[/latex]

(10.48)

Où les sous-matrices (3×6), A et B sont respectivement connues comme jacobiennes d’orientation et de position.

Plus tôt dans cette section, nous avons supposé uniquement des articulations rotoïdes pour calculer le jacobien d’un manipulateur sériel. Si une articulation i^th est plutôt prismatique, les vitesses angulaires et linéaires du lien i^th sont écrites comme :

[latex]\begin{equation} \boldsymbol\omega_i=\boldsymbol\omega_{i-1},\quad \dot{\mathbf{a}}_i=\boldsymbol\omega_{i-1}\times\mathbf{a}_i+\dot{d}_i\mathbf{e}_i \end{equation}[/latex]

(10.49)

On peut alors prouver que le membre cotisant de l’articulation i^th au jacobien, c’est-à-dire la i^th colonne, s’exprime sous la forme :

[latex]\begin{equation} \mathbf{j}_i=\begin{bmatrix} \mathbf{0}\\\mathbf{e}_i \end{bmatrix} \end{equation}[/latex]

(10.50)

10.4.4.1 Exemple : Jacobien d’un manipulateur sériel à 6 DDL à poignet à axes concourants

Étant donné que les axes des dernières articulations d’un manipulateur sériel à poignet `a´ axes concourants se croisent en un point, appelé poignet sphérique, sa matrice jacobienne est simplifiée, ce qui donne :

[latex]\begin{equation} \mathbf{J}=\begin{bmatrix} \mathbf{J}_{11} & \mathbf{J}_{12}\\\mathbf{J}_{21} & \mathbf{0} \end{bmatrix} \label{e:wp_Jacobian} \end{equation}[/latex]

(10.51)

Où 0, J₁₁, J₁₂et J₂₁sont des matrices (3 × 3). Vous devez noter que pour simplifier les équations, la matrice jacobienne donnée ici cartographie les taux de l’articulation dans la torsion de P_w, à savoir l’emplacement de l’intersection des axes des trois dernières articulations. Par conséquent, nous avons:

[latex]\begin{equation} \mathbf{t}_w=\mathbf{J}\dot{\mathbf{q}} \end{equation}[/latex]

(10.52)

Où t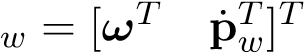. Comme vous pouvez le constater, le vecteur de vitesse angulaire ω n’est pas fonction de l’emplacement de P_w. La vitesse linéaire de P_w, qui n’est fonction que des trois premières vitesses de l’articulation, est calculée avec l’équation suivante, c’est-à-dire :

[latex]\begin{equation} \dot{\mathbf{p}}_w = \dot{q}_1\mathbf{e}_1\times\mathbf{r}_1+\dot{q}_2\mathbf{e}_2\times\mathbf{r}_2+\dot{q}_3\mathbf{e}_3\times\mathbf{r}_3 \end{equation}[/latex]

(10.53)

Où r_iest défini comme le vecteur du repère DH i^th au P_w et e_i est le vecteur unitaire parallèle à l’axe de l’articulation i^th, comme mentionné ci-dessus. La vitesse angulaire de l’organe effecteur est calculée à l’aide de la formule indiquée plus haut dans cette section, c’est-à-dire:

[latex]\begin{equation} \boldsymbol\omega = \dot{{q}}_1\mathbf{e}_1+\dot{{q}}_2\mathbf{e}_2+\dot{{q}}_3\mathbf{e}_3+\dot{{q}}_4\mathbf{e}_4+\dot{{q}}_5\mathbf{e}_5+\dot{{q}}_6\mathbf{e}_6 \end{equation}[/latex]

(10.54)

Par conséquent, nous pouvons déterminer que les sous-matrices incluses dans l’expression (10.51) sont :

[latex]\begin{align} \mathbf{J}_{11}&=\begin{bmatrix}\mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \end{bmatrix}\\ \end{align}[/latex]

(10.55a)

[latex]\begin{align} \mathbf{J}_{12}&=\begin{bmatrix}\mathbf{e}_4 & \mathbf{e}_5 & \mathbf{e}_6 \end{bmatrix}\\ \end{align}[/latex]

(10.55b)

[latex]\begin{align} \mathbf{J}_{21}&=\begin{bmatrix}\mathbf{e}_1\times\mathbf{r}_1 & \mathbf{e}_2\times\mathbf{r}_2 & \mathbf{e}_3\times\mathbf{r}_3 \end{bmatrix}\\ \end{align}[/latex]

(10.55c)

10.4.5 Singularités

En robotique, lorsqu’un manipulateur est dans une posture singulière, ou simplement dans une singularité, il ne peut pas déplacer son organe effecteur le long d’au moins dans une direction. Mathématiquement, cela correspond à une matrice jacobienne singulière utilisée pour calculer les vitesses de l’articulation. Nous avons supposé précédemment que cette matrice était non singulière, c’est-à-dire que pour un robot à 6 degrés de liberté, son jacobien est inversible et son déterminant n’est pas égal à zéro (Section 6.4). Ce n’est peut-être pas le cas pour certaines configurations. Au-delà là de la question numérique de l’inversion d’une matrice singulière, la posture correspondante du robot a aussi une signification physique liée aux limites de l’espace de travail du robot ou à une perte de mobilité, comme mentionnée ci-dessus. De plus, si l’on se réfère aux types de configuration évoqués plus haut dans ce chapitre, les singularités correspondent aux limites entre ces entités au sein de l’espace de travail du robot.Une posture proche d’une singularité est également problématique pour un manipulateur et un robot en général, car le déterminant de sa matrice jacobienne sera proche de zéro, donnant une division par un nombre proche de zéro. Cela se traduira par des vitesses des articulations considérablement élevées, ce qui suscite des inquiétudes quant à la sécurité et réduit la précision du suivi de la trajectoire. Comme :

[latex]\mathbf{t}=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}[/latex]

(10.56)

Où q˙, t et J(q) sont respectivement le vecteur de taux articulaire n-dimensionnel, la torsion d’organe effecteur à6 dimensions et la matrice jacobienne 6 × n, où n est le nombre d’articulations. Il est donc trivial de constater que toute torsion d’organe effecteur réalisable donnée, à savoir sa vitesse linéaire et angulaire, telle que définie à la section 10.4.4, est une combinaison linéaire des vitesses des articulations. Pour pouvoir atteindre n’importe quelle valeur arbitraire de t, le rang de J, qui est fonction de la posture du robot, c’est-à-dire q, doit être égal à6 pour un robot dans l’espace 3D. Si c’est le cas, n’importe quelle torsion donnée de l’organe effecteur est réalisable. Cependant, il convient de noter que puisque le jacobien dépend de la posture, ce n’est pas toujours le cas. Si le rang(J) devient inférieur à6, c’est ce qu’on appelle une posture singulière, ou, par souci de brièveté, une singularité. Selon la partie de la matrice jacobienne qui génère une singularité, on peut avoir une singularité de position ou d’orientation, chacune ayant une interprétation physique différente.

10.4.5.1 Singularité de la position jacobienne

Pour un manipulateur sériel à 6 DDL à axes concourants, une singularité de la sous-matrice J₂₁entraîne une singularité de position, correspondant à l’impossibilité de calculer les taux d’articulation pour cette localisation. Cela se produit lorsque le déterminant de J₂₁est égal à zéro. Considérant eq. (10.51), le déterminant peut s’écrire comme :

[latex]\begin{equation} \det(\mathbf{J}_{21})=(\mathbf{e}_1\times\mathbf{r}_1)\times(\mathbf{e}_2\times\mathbf{r}_2)\times(\mathbf{e}_3\times\mathbf{r}_3)=0 \end{equation}[/latex]

(10.57)

Ce cas peut se produire dans deux situations. Tout d’abord, vous trouverez ce type de singularité lorsqu’une colonne de J₂₁est égale à zéro, par exemple lorsque e_i et r₁sont parallèles, ce qui est communément appelé une singularité d’épaule. Ce cas particulier correspond physiquement au centre du poignet étant situé sur le premier axe de l’articulation, entraînant la perte instantanée d’un DDL. Cela peut aussi être vrai pour la deuxième ou la troisième articulation (le centre du poignet étant situé sur la i^th l’axe de l’articulation), mais cela est généralement évité en concevant soigneusement le manipulateur.Sinon, on peut aussi avoir det(J₂₁) = 0 quand deux colonnes de J₂₁deviennent coplanaires, ce qui entraîne un défaut de rang. De multiples postures/configurations du robot peuvent conduire à cette situation, notamment, mais pas seulement, un bras en pleine extension à la limite de l’espace de travail atteignable. Cela comprend des singularités du coude, qui se produisent pour les manipulateurs articulés verticalement^[8], comme le Meca500 commercialisé par Mecademics^[9] lorsque le centre du poignet se trouve sur le plan passant par les deuxième et troisième axes. Cela peut également arriver en théorie avec le manipulateur replié sur lui-même, mais des limites mécaniques empêchent normalement cette situation de se produire.

10.4.5.2 Singularité de l’orientation jacobienne

Dans le cas d’un manipulateur à poignet à axes concourants, une singularité d’orientation se produit lorsque det(J₁₂) = 0. Cela ne peut se produire que lorsque e₄, e₅et e₆sont coplanaires. Dans cette configuration, seul le vecteur de vitesse angulaire sur le plan généré par les trois vecteurs mentionnés ci-dessus est possible à l’organe effecteur. Compte tenu de la chaîne cinématique typique d’un manipulateur sériel à poignet à axes concourants, cela se produit généralement lorsque les axes des quatrième et sixième articulations rotoïdes coïncident. Ce type de singularité est parfois appelé une singularité de poignet.

10.4.5.3 Singularités avec un manipulateur qui n’est pas à poignet à axes concourants

Nous avons maintenant compris les différentes singularités au sein de l’espace de travail d’un manipulateur sériel à poignet à axes concourants à travers une analyse de son jacobien. Mathématiquement, vous pouvez appliquer le même processus pour trouver des singularités dans l’espace de travail d’un manipulateur qui n’est pas à poignet à axes concourants. Cependant, dans ce cas, nous examinerons la matrice jacobienne complète, car nous n’avons pas de cinématique découplée pour l’orientation et la position. Dans cette optique, nous utiliserons le Kinova Gen3 lite, mentionné précédemment pour illustrer le processus. Les postures singulières potentielles sont représentées sur la figure 10‑5.

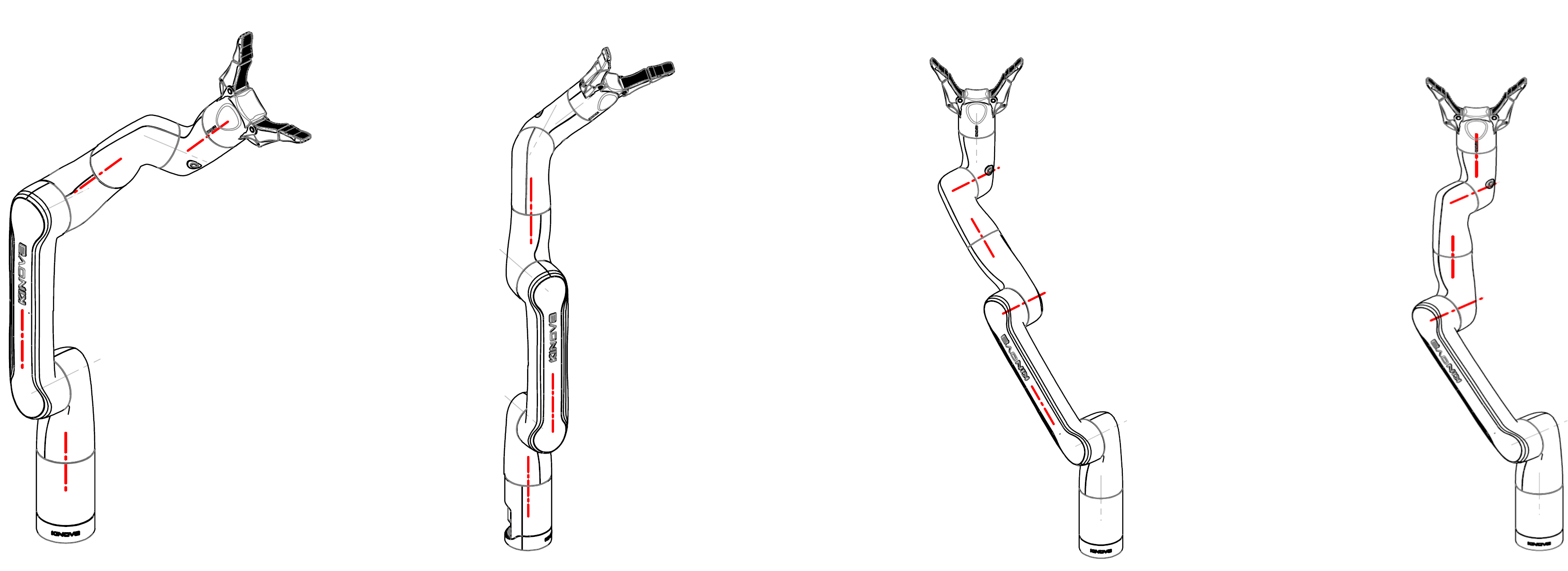
Figure 10‑5 : Postures singulières du Kinova Gen3 lite (extraites du manuel de l’utilisateur)

Dans cette figure, de gauche à droite, nous avons quatre configurations différentes correspondant à des singularités de la matrice jacobienne qui diffèrent d’un bras complètement étendu, une autre configuration singulière. De gauche à droite (tous les axes cités sont illustrés en rouge sur la figure),L’axe de la première articulation et l’axe X du troisième repère DH, c’est-à-dire la perpendiculaire commune entre les axes des articulations 2 et 3, sont parallèles; les axes des articulations 4 et 6 sont également parallèles;Les axes des première et quatrième articulation sont tous deux parallèles à la perpendiculaire commune entre les axes des articulations 2 et 3;Les axes des troisième et cinquième articulation sont parallèles; la quatrième articulation est également parallèle à la perpendiculaire commune entre les axes des articulations 2 et 3;L’axe de la troisième articulation est parallèle au cinquième axe d’articulation et le quatrième axe d’articulation est parallèle au sixième axe d’articulation.Les quatre cas illustrés ci-dessus impliquent un double alignement dans la posture du Gen3 Lite, qui perd momentanément un DDL. Par exemple, dans le deuxième cas, l’organe effecteur ne peut pas se déplacer dans la direction du quatrième axe d’articulation. Dans les troisième et quatrième cas, le mouvement est impossible dans la direction de l’axe de la troisième articulation.

10.5 Cinématique des manipulateurs parallèles

Comme nous l’avons mentionné au début de ce chapitre, les manipulateurs parallèles sont connus pour leur rigidité structurelle, leur vitesse et leur capacité à soulever une charge utile plus importante que les manipulateurs sériels de masse et de taille similaires. Alors que leur architecture est composée d’au moins une boucle, ils en ont généralement plus. Parmi les architectures parallèles bien connues, les trois branches Delta (parfois dotées d’un cardan télescopique pour ajouter un quatrième DDL) (Clavel, 1990) ainsi que les quatre membres Par4 (Pierrot et al, 2003) (Adept Quattro) ont été brevetés et commercialisés. Avant de commencer avec la cinématique des manipulateurs parallèles, il faut savoir que l’organe effecteur d’un robot parallèle est communément appelé la plate-forme mobile (ou mobile), étant donné qu’elle est fixée à la base à l’aide de plusieurs membres.

Figure 10‑6 : robot paralléle PPR-2PRP, de (Joubair et al, 2012)

10.5.1 Cinématique directe et inverse

Alors que la résolution de la cinématique directe d’une chaîne cinématique sérielle est généralement une tâche simple, ce n’est pas le cas avec les robots parallèles. En effet, l’outil que nous avons utilisé dans la section 10.4.2, la convention Denavit-Hartenberg, n’est pas approprié pour les manipulateurs parallèles, car il n’accepte qu’un maximum de deux articulations pour chaque lien. En général, il n’est pas possible d’obtenir une fonction explicite des coordonnées cartésiennes de l’organe effecteur par rapport aux coordonnées des articulations, même pour un simple robot parallèle. Par conséquent, les méthodes itératives sont couramment utilisées à cette fin.Contrairement à la cinématique directe, la résolution de la cinématique inverse d’un robot parallèle est généralement moins difficile qu’avec un robot série. Nous obtiendrons une fonction implicite égale à zéro où q et p sont les variables, c’est-à-dire :

[latex]\begin{equation} \mathbf{f}(\mathbf{q},\mathbf{p})=\mathbf{0} \label{e:parallel_kinematics} \end{equation}[/latex]

(10.58)

10.5.1.1 Exemple : Cinématique d’un robot parallèle PPR-2PRP

Voici un robot parallèle planaire avec trois articulations prismatiques actionnées, reliées à trois membres attachés à la plate-forme mobile, représenté sur la figure 10-6 et la figure 10-7. L’une est une chaîne PPR, tandis que les deux autres sont des chaînes PRP. Les coordonnées de la plateforme mobile sont (x,y,θ), et les coordonnées de l’articulation sont (ρ₁,ρ₂,ρ₃). Il faut donc trouver des expressions de la première en fonction de la seconde. En utilisant des relations de géométriques simples, nous avons :

[latex]\begin{align} \theta =& \arctan\left(\frac{\rho_3+d_3-\rho_2}{s}\right)\\ \end{align}[/latex]

(10.59a)

[latex]\begin{align} x =& \rho_1+d_1 \end{align}[/latex]

(10.59b)

Pour la dernière coordonnée cartésienne, sachant:

[latex]\begin{equation} \frac{h}{x}=\frac{l}{s} \end{equation}[/latex]

(10.60)

Nous pouvons calculer:

[latex]\begin{equation} y = \rho_2+(\rho_1+d_1)\frac{\rho_3+d_3-\rho_2}{s} \end{equation}[/latex]

(10.61)

Ces trois expressions ci-dessus représentent la solution au FKP. La solution à la cinématique robot parallèle inverse est simple à partir de ce point :

[latex]\begin{align} \rho_1=&x-d_1\\ \end{align}[/latex]

(10.62a)

[latex]\begin{align} \rho_2=&y-x\tan\theta\\ \end{align}[/latex]

(10.62b)

[latex]\begin{align} \rho_3=&y+(s-x)\tan\theta-d_3 \end{align}[/latex]

(10.62c)

10.5.2 Jacobiens

Comme mentionné ci-dessus, le modèle cinématique d’un robot parallèle est généralement exprimé sous la forme d’une fonction implicite, à savoir eq. (10.58). En le différenciant par rapport au temps, on a :

[latex]\begin{equation} \mathbf{J}\dot{\mathbf{p}}=\mathbf{K}\dot{\mathbf{q}} \end{equation}[/latex]

(10.63)

Où les deux J et K sont des matrices jacobiennes.

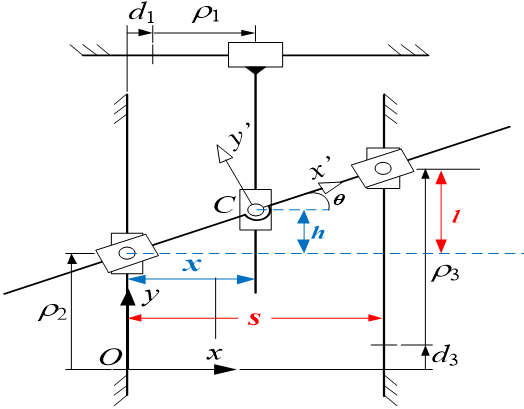
Figure 10‑7 : Géométrie d’un robot parallèle PPR-2PRP, de (Joubair et al, 2012)

10.5.3 Singularités

À partir de ces deux matrices jacobiennes, on peut définir trois types de singularités :

Type I : quand K est singulier, c’est-à-dire det(K) = 0. Cela correspond généralement à une limite de l’espace de travail accessible ou à une limite interne de l’espace de travail où se rencontrent deux branches de solutions à la cinématique inverse. Par conséquent, certaines vitesses cartésiennes à l’organe effecteur ne pourront pas être générées.
Type II : quand J est singulier, c’est-à-dire det(J) = 0. Ces singularités se produisent à des emplacements dans l’espace de travail accessible où deux branches de solutions au FKP se rencontrent. Par conséquent, même pour des coordonnées d’articulation fixes, un mouvement infinitésimal de l’organe effecteur est possible. Cela signifie également que le robot ne peut pas équilibrer certaines clés externes appliquées à l’organe effecteur, entraînant ainsi une perte de contrôle qu’il faut absolument éviter.
Type III : une combinaison des deux types ci-dessus, donc quand det(J) = det(K) = 0. Dans ce cas, eq. (10.58) dégénère, se soldant en un organe effecteur inutilisable. Ce type de singularité n’existe que pour certaines architectures.

La figure 10-8 représente des postures singulières d’un pantographe, un mécanisme commun à cinq barres qui peut être utilisé comme un manipulateur parallèle planaire. L’organe effecteur est sur l’articulation rotoïde médiane et les deux articulations rotoïdes fixées à la base peuvent être actionnées. Comme on peut le constater sur cette figure, l’organe effecteur ne peut pas monter plus haut puisque le mécanisme est complètement étendu pour la singularité de type I illustrée. Dans le cas de la posture singulière de type II représentée, il est impossible de contrôler le mouvement vertical de l’organe effecteur. Avec une petite perturbation, l’organe effecteur pourrait se déplacer vers le haut ou le bas pour les mêmes vitesses des articulations de base actionnées.

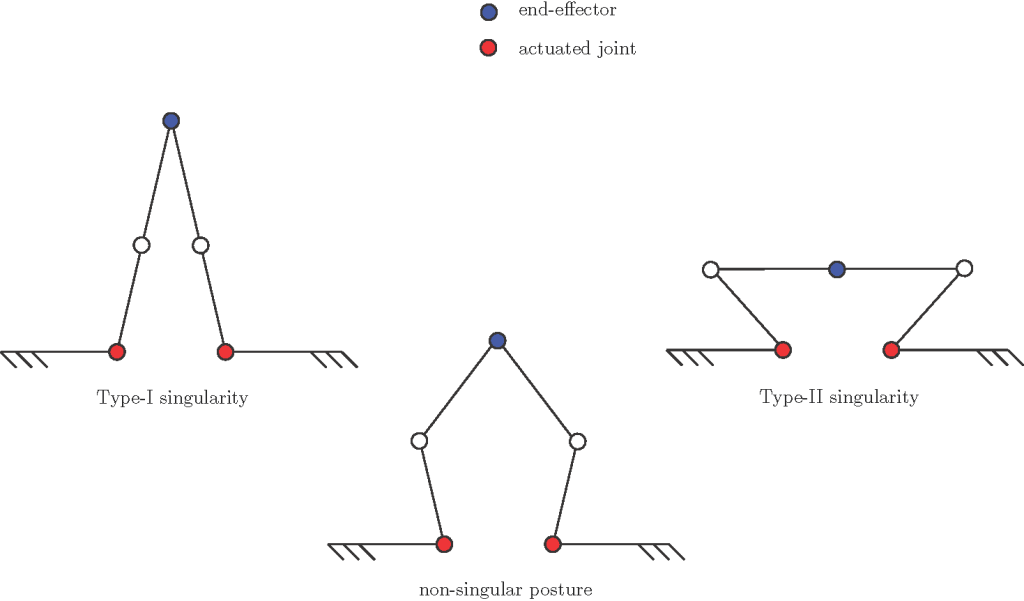
Figure 10‑8 : Pantographe, un manipulateur parallèle planaire à 2 DDL.

10.6 Dynamique

Selon le dictionnaire Merriam-Webster, la dynamique est “une branche de la mécanique qui traite des forces et de leur relation principalement avec le mouvement, mais parfois aussi avec l’équilibre des corps.”^[10] Les forces peuvent être linéaires, mais aussi rotatives, à savoir le couple. La deuxième loi de Newton est particulièrement importante lorsqu’il s’agit de l’analyse quantitative de la dynamique d’un système, car elle stipule que “le taux de variation dans le temps de la quantité de mouvement d’un corps est égal en amplitude et en direction à la force qui lui est imposée.”^[11] Comme pour la cinématique, nous pouvons définir deux problèmes différents :

dynamique directe, à partir des actionneurs au mouvement, utile pour les simulations;
dynamique inverse, à partir du mouvement aux actionneurs, indispensable au contrôle.

Dans ce chapitre, nous fournirons un aperçu de deux approches pour calculer le modèle dynamique d’un robot, à savoir les méthodes d’Euler-Lagrange et de Newton-Euler.

10.6.1 Euler-Lagrange

La méthode d’Euler-Lagrange est basée sur l’énergie. Le Lagrangien est défini comme :

[latex]\begin{equation} \cal{L}=T-V \end{equation}[/latex]

(10.64)

Où T et V sont respectivement les énergies cinétique et potentielle totales du système. À partir du lagrangien, les équations dynamiques définissant le mouvement du robot sont calculées avec :

[latex]\begin{equation} \frac{d}{dt}(\frac{\partial L}{\partial\dot{q}_i})-\frac{\partial L}{\partial q_i}=\tau_i \end{equation}[/latex]

(10.65)

Où q_iet τ_i sont, respectivement, les coordonnées des articulations généralisées et le couple (ou la force pour une articulation prismatique).

10.6.1.1 Exemple : Euler-Lagrange appliqué à un manipulateur planaire à2 degrés de liberté

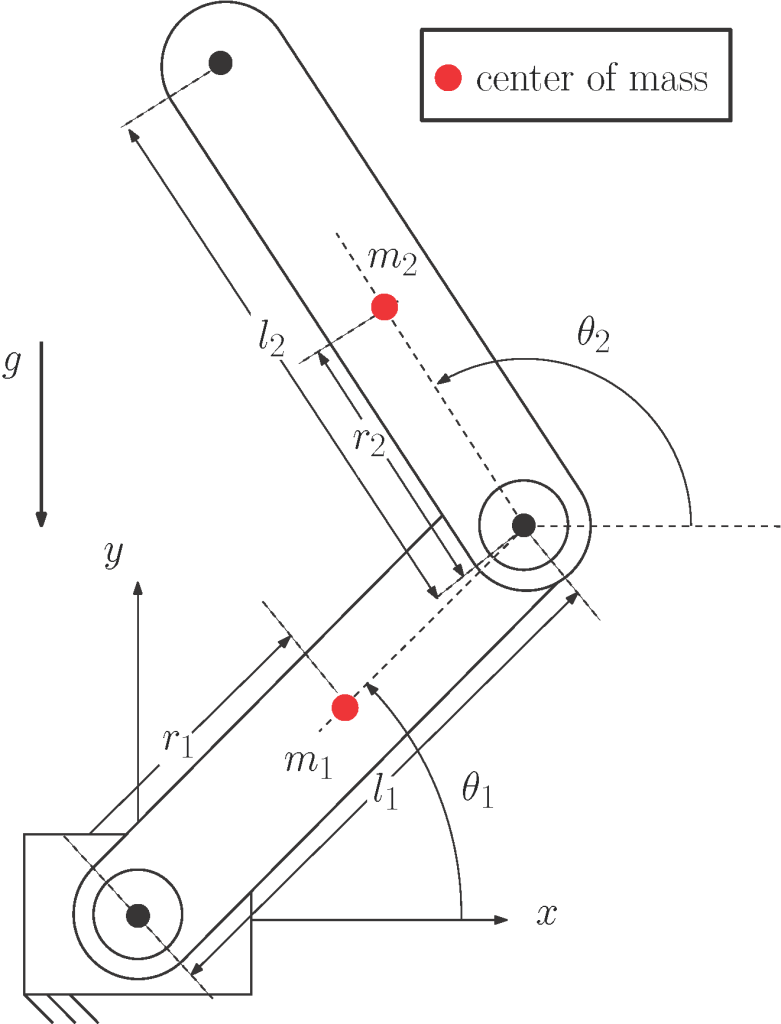
Figure 10‑9 : Géométrie d’un robot série à 2 degrés de liberté

Un simple manipulateur sériel planaire à 2 degrés de liberté est illustré à la figure 10-9. Pour les fins de cet exemple, seule la masse de chaque lien est considérée, et non leur moment d’inertie. L’expression de la cinétique totale est

[latex]K= K_1+K_2=\frac{1}{2}m_1 {v}_1^2 + \frac{1}{2}m_2 {v}_2^2[/latex]

(10.66)

Où v₁et v₂représentent l’ampleur de la vitesse linéaire des masses m₁et m₂, respectivement. On sait, compte tenu de la géométrie, que

[latex]\begin{align} v_1^2=& \dot{x}_1^2+\dot{y}_1^2 = r_1^2\dot{\theta}_1^2\\\end{align}[/latex]

(10.67a)

[latex]\begin{align} v_2^2=& \dot{x}_2^2+\dot{y}_2^2\\ \end{align}[/latex]

(10.67b)

[latex]\begin{align} \dot{x}_2 =& (-l_1\sin\theta_1-r_2\sin(\theta_1+\theta_2))\dot{\theta}_1-r_2\sin(\theta_1+\theta_2)\dot{\theta}_2\\ \end{align}[/latex]

(10.67c)

[latex]\begin{align} \dot{y}_2 =& (l_1\cos\theta_1+r_2\cos(\theta_1+\theta_2))\dot{\theta}_1+r_2\cos(\theta_1+\theta_2)\dot{\theta}_2 \end{align}[/latex]

(10.67d)

Où m₁, r₁, l₁, l₂, r₂, m₂et g représentent respectivement les masses, les distances entre l’origine de chaque lien et son CoM et les longueurs des premier et deuxième liens et l’accélération gravitationnelle. L’énergie cinétique totale est donc :

[latex]\begin{align} K= \frac{1}{2}m_1 r_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2 \left((l_1^2+2l_1l_2\cos\theta_2+l_2^2)\dot{\theta}_1^2+2(l_2^2+l1l_2\cos\theta_2)\dot{\theta}_1\dot{\theta}_2+l_2^2\dot{\theta}_2^2)\right) \end{align}[/latex]

(10.68)

Enfin, en considérant toujours la géométrie, l’énergie potentielle totale est :

[latex]\begin{align} T=T_1+T_2=m_1 g l_1 \sin\theta_1 + m_2 g \left(l_1\sin\theta_1 + l_2\sin(\theta_1+\theta_2)\right) \end{align}[/latex]

(10.69)

Vous pouvez effectuer la procédure sous forme d’exercice.

10.6.2 Newton-Euler

L’approche Newton-Euler est une méthode récursive. Vous calculez d’abord les vitesses et les accélérations angulaires et linéaires de chaque lien individuellement dans le repère inertiel, en partant de la base. Ensuite, les forces et couples appliqués par chaque lien sur le précédent sont calculés, en partant de l’organe effecteur. Elle est utilisée ici pour résoudre la dynamique inverse des manipulateurs sériels.

10.6.2.1 Vitesses et accélérations

Tout d’abord, il convient de noter que dans cette procédure, c’est la vitesse et l’accélération du centre de masse (CoM) de chaque corps, et non du repère, que vous devez calculer. Les vitesses et les accélérations sont obtenues à l’aide de l’algorithme 1. Dans ce tableau, les composantes des vecteurs a_i et e_i (cf. figure 10-2) dans le repère (i + 1) sont :

[latex]\begin{align} [\mathbf{e}_i]_{i+1}=\begin{bmatrix} 0 & \sin\alpha_i & \cos\alpha_i \end{bmatrix}^T\\ \end{align}[/latex]

(10.70a)

[latex]\begin{align} [\mathbf{a}_i]_{i+1}=\begin{bmatrix} a_i & b_i\sin\alpha_i & b_i\cos\alpha_i \end{bmatrix}^T \end{align}[/latex]

(10.70b)

Algorithm 1 Vitesses et accélérations

Require: [ω₀]₁, [c˙₀]₁,[ω˙ ₀]₁and [c¨₀]₁

for i = 1 to n do

if i^th l’articulation est rotoïde then

[ωi]i+1 ← QTi [ωi−1]i + θ˙i[ei]i+1

[c˙_i]_i+1 ← Q^T_i [c˙_i−1]_i + [ω_i]_i+1 × [(a_i+ s_i)]_i+1 − Q^T_i [ω_i−1 × s_i−1]_i

[ω˙ _i]_i+1 ← Q^T_i [ω˙ _i−1]_i + θ^¨_i[e_i]_i+1 + θ^˙_i(Q^T_i [ω_i−1]_i) × [e_i]_i+1

[c¨i]i+1 ← QTi [c¨i−1]i + [ω˙ i]i+1 × [(ai + si)]i+1 + [ωi]i+1 × [ωi]i+1 × [(ai + si)]i+1 −

Q^T_i [ω˙ _i−1 × (ω_i−1 × s_i−1)]_i

else if i^th l’articulation est prismatique then

[ω_i]_i+1 ← Q^T_i [ω_i−1]_i

[c˙_i]_i+1 ← Q^T_i [c˙_i−1]_i + [ω_i]_i+1 × [(a_i+ s_i)]_i+1 + d^˙_i[e_i]_i+1 − Q^T_i [ω_i−1 × s_i−1]_i [ω˙ _i]_i+1 ← Q^T_i [ω˙ _i−1]_i

[c¨i]i+1 ← QTi [c¨i−1]i + [ω˙ i]i+1 × [(ai + si)]i+1 + [ωi]i+1 × [ωi]i+1 × [(ai + si)]i+1 −

Q^T_i [ω˙ _i−1 × (ω_i−1 × s_i−1)]_i + 2[ω_i]_i+1 × b^˙_i[e_i]_i+1 +^¨b_i[e_i]_i+1

end if

end for

10.6.2.2 Forces et Moments

L’étape suivante consiste à calculer les forces et les moments sur chaque lien, en commençant par l’organe effecteur. La clé appliquée par le lien (i − 1)^th sur le lien i^th est définie comme :

[latex]\begin{equation} \mathbf{w}_i=\begin{bmatrix} \mathbf{n}_i^T & \mathbf{f}_i^T \end{bmatrix}^T \end{equation}[/latex]

(10.71)

Où les vecteurs tridimensionnels n^T_i et f_i^T , sont respectivement la force et le moment associés à cette clé. Une composante de chaque clé est l’actionnement associé à l’articulation correspondante, à savoir la troisième composante pour une articulation rotoïde et la sixième articulation pour une articulation prismatique. Les composantes restantes sont la force de réaction et le moment entre les deux liens. La procédure pour calculer la clé sur chaque lien est détaillée dans l’algorithme 2. Vous vous demandez peut-être où l’effet de la gravité apparaît dans l’algorithme. Pour simplifier la procédure tout en obtenant une solution équivalente, nous utilisons une astuce simple. Ici, on suppose une accélération virtuelle −g à la base du robot, à savoir le premier lien. Par conséquent, même si la base est fixe et ne bouge pas, nous avons :

[latex]\begin{equation} [\ddot{\mathbf{c}}_0]_1 = [-\mathbf{g}]_1 \end{equation}[/latex]

(10.72)

Où −g représente l’accélération gravitationnelle.

Algorithm 2 Clé sur chaque lien

[fn]n ← Qn[mnc¨n − f]n+1

[nn]n ← Qn[Inω˙ n + ωn × Inωn − n + (an + sn) × fn]n+1

for i = n − 1 to 1 do

[fi]i ← Qi[mic¨i + fi+1]i+1

[fi]i+1 ← Qi[fi]i

[ni]i ← Qi[Iiω˙ i + ωi × Iiωi + ni+1 + (ai + si) × fi − si × fi+1]i+1

end for

Nous avons maintenant toutes les forces f_iet moments n_i, l’étape finale consiste donc à calculer ce que nous recherchions au départ, les couples d’actionnement pour les articulations rotoïdes et les forces d’actionnement pour les articulations prismatiques. Cela est effectué avec les deux équations suivantes :

[latex]\begin{align} \tau_i =& \mathbf{e}_i^T\mathbf{n}_i,\quad\textrm{pour les articulations rotoïdes}\\ \end{align}[/latex]

(10.73a)

[latex]\begin{align} \tau_i =& \mathbf{e}_i^T\mathbf{f}_i,\quad\textrm{pour les articulations prismatiques} \end{align}[/latex]

(10.73b)

10.7 Résumé du chapitre

Dans ce chapitre, nous avons fourni une introduction aux principes fondamentaux des manipulateurs robotiques, du point de vue de la mécanique. Nous avons d’abord présenté les architectures typiques; série et parallèle, leurs avantages et inconvénients, ainsi que les caractéristiques notables telles que leurs degrés de liberté et le type de mouvement qu’elles peuvent générer. Ensuite, nous nous sommes concentrés sur la cinématique des deux catégories, des articulations à organe effecteur (cinématique directe) et inversement (cinématique inverse). Si des approches standards existent à la fois pour la cinématique directe et inverse d’un manipulateur sériel, notamment s’il est à poignet à axes concourants, ce n’est pas le cas.

Pour leurs homologues parallèles. Cependant, la cinématique inverse d’un robot parallèle peut généralement être résolue plus facilement. Nous avons étudié les relations entre les vitesses des articulations et la torsion de l’organe effecteur, qui comprend ses vitesses angulaire et linéaire. Ces équations peuvent être assemblées pour obtenir la matrice jacobienne, un outil utile dans l’analyse des robots série et parallèle. En effet, à partir de cette matrice, on peut trouver des postures singulières du robot : ces configurations doivent être évitées, car elles peuvent engendrer des problèmes de sécurité et de contrôle. Enfin, nous avons rédigé un aperçu de la dynamique des manipulateurs robotiques, à savoir deux approches courantes, Euler-Lagrange et Newton-Euler.

10.8 Questions de révision

Tableau 10‑2: Paramètres DH d’un manipulateur 6R à poignet à axes concourants

i	1	2	3	4	5	6
a_i	0	135 mm	38 mm	0	0	0
d_i	135 mm	0	0	120 mm	0	70 mm
α_i	−π/2	0	−π/2	π/2	π/2	0
θ_i	q1	q₂− π/2	q3	q4	q₅+ π	q6

10.9 Lectures complémentaires

Ce chapitre ne vous a donné qu’un bref résumé de la mécanique des manipulateurs robotiques. Si vous souhaitez en savoir plus, vous pouvez d’abord consulter la notation DH originale et àses variantes. A cet effet, vous pouvez vous reporter à un article publié par Harvey Lipkin (Lipkin, 2008). De plus, étant donné que nous ne sommes pas entrés dans les détails de la dynamique des robots, une littérature abondante peut-être trouvée sur ce sujet. Notamment, vous pouvez consulter les équations de Kane, similaires à l’approche lagrangienne. Aussi, Angeles (2014) a introduit une méthode alternative pour résoudre la dynamique inverse d’un système robotique, le complément orthogonal naturel (CNO). En ce qui concerne les outils mathématiques utiles à l’analyse de la mobilité, de la cinématique et de la dynamique des systèmes et mécanismes robotiques, vous pouvez consulter la théorie des groupes (Angeles, 2014), théorie de la vis(Davidson, 2004; Müller, 2017), à l’origine du concept de torsion et de clé, et l’algèbre à deux nombres, utile pour combiner une translation et une rotation en une seule variable. Enfin, vous pouvez également vous pencher sur le concept de singularités de contrainte pour les mécanismes parallèles (Zlatanov et al, 2002).

Références

Angeles J (2014) Fundamentals of Robotic Mechanical Systems, Mechanical Engineering Series, vol 124. Springer International Publishing, Cham, DOI 10.1007/978-3-319-01851-5

Clavel R (1990) Device for the movement and positioning of an element in space

Davidson JK (2004) Robots and screw theory: applications of kinematics and statics to robotics. Oxford University Press, Oxford

Forsythe GE (1970) Pitfalls in Computation, or Why a Math Book isn’t Enough. The American Mathematical Monthly 77(9):931–956, DOI 10.1080/00029890.1970.11992636

Gosselin C, Liu H (2014) Polynomial Inverse Kinematic Solution of the Jaco Robot. In: ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, ASME, Buffalo, NY, p V05BT08A055, DOI 10.1115/detc201434152

Hartenberg R, Denavit J (1964) Kinematic Synthesis of Linkages. McGraw-Hill Book Company, New York

Joubair A, Slamani M, Bonev IA (2012) A novel XY-Theta precision table and a geometric procedure for its kinematic calibration. Robotics and Computer-Integrated Manufacturing 28(1):57–65, DOI 10.1016/J.RCIM.2011.06.006

Lipkin H (2008) A Note on Denavit-Hartenberg Notation in Robotics. Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference – DETC2005 7 B:921–926, DOI 10.1115/DETC200585460

Makino H, Kato A, Yamazaki Y (2007) Research and commercialization of SCARA RobotThe case of industry-university joint research and development. International Journal of Automation Technology 1:61–67

Müller A (2017) Screw Theory – A forgotten Tool in Multibody Dynamics. PAMM 17(1):809– 810, DOI 10.1002/PAMM.201710372

Pierrot F, Shibukawa T, Morita K (2003) Four-degree-of-freedom parallel robot

Zlatanov D, Bonev IA, Gosselin CM (2002) Constraint singularities of parallel mechanisms. Proceedings – IEEE International Conference on Robotics and Automation 1:496–502, DOI 10.1109/ROBOT.2002.1013408

Téléchargez les références : ↓

Liste des figures

Figure 10‑1 : Kinova Gen3 lite, un manipulateur robotique sériel à 6 DDL

Figure 10‑2 : Représentation des repères dans la convention DH

Figure 10‑3 : Les repères DH pour chaque articulation du Kinova Gen3 lite (extrait du manuel d’utilisation du manipulateur)

Figure 10‑4 : Postures possibles pour la même position d’organe effecteur

Figure 10‑5 : Postures singulières du Kinova Gen3 lite (extraites du manuel de l’utilisateur)

Figure 10‑6 : PPR-2PRP

Figure 10‑7 : Géométrie d’un robot parallèle PPR-2PRP

Figure 10‑8 : Pantographe, un manipulateur parallèle planaire à 2 DDL

Figure 10‑9 : Géométrie d’un robot série à 2 degrés de liberté

Liste des tableaux

Tableau 10‑1 : Paramètres DH du Kinova Gen3 lite

Tableau 10‑2 : Paramètres DH d’un manipulateur 6R à poignet à axes concourants

Attribution

Les figures ci-dessous sont utilisées dans ce manuel avec permission du détenteur des droits d’auteur.

Cette permission n’est pas transférable, il est de la responsabilité du prochain utilisateur de faire les démarches nécessaires auprès du détenteur des droits pour obtenir les permissions d’utilisation :

Figure 10‑1

Figure 10‑3

Figure 10‑4

Figure 10‑5

Figure 10‑6

Figure 10‑7

Une lettre soulignée représentant une articulation signifie qu’elle est actionnée. ↵
Comme nous l’avons expliqué au chapitre 4, le pouce de la main droite pointe dans la direction de l’axe Z; la courbure des doigts lors de la fermeture de la main représente un mouvement de l’axe X vers l’axe Y. ↵
toujours positif par définition ↵
Étant une distance signée, elle peut être négative. ↵
Trois de ses six articulations seront verrouillées. ↵
Un manipulateur redondant spatial à architecture série dispose de plus de 6 articulations. Nonobstant les limites mécaniques des articulations, les limites de l’espace de travail accessible et des singularités, seulement six articulations sont nécessaires pour atteindre n’importe quel point avec n’importe quelle orientation de l’EE. Vous devez être prudent si vous rencontrez le terme ” redondant ”, car il peut avoir différentes significations selon le contexte. Un robot à architecture parallèle peut être actionné de manière redondante, c’est-à-dire plus d’actionneurs que de degrés de liberté, et n’importe quel manipulateur peut être cinématiquement redondant par rapport à sa tâche, par exemple les tâches de pointage, qui ne nécessitent que deux degrés de liberté. ↵
Section 6.10 ↵
Une architecture articulée verticalement est courante pour les manipulateurs en série à poignet à axes concourants avec 6 axes et disponibles sur le marché: les axes de la deuxième et de la troisième articulations sont parallèles, les axes des première et quatrième articulations sont orthogonaux aux axes des deuxième et troisième articulations et l’axe de la cinquième articulation est orthogonal aux axes des quatrième et sixième articulations. ↵
https://www.mecademic.com/en/what-are-singularities-in-a-six-axis-robot-arm ↵
www.merriam-webster.com/dictionary/dynamics ↵
Définition de Britannica ↵

Licence

Symbole de License Creative Commons Attribution - Pas d’utilisation commerciale - Partage dans les mêmes conditions 4.0 International

Fondements de la robotique Copyright © 2022 by Damith Herath et David St-Onge. Traduction de l’édition anglaise : Foundations of Robotics – A Multidisciplinary Approach with Python and ROS. Copyright © Dr. Damith Herath, Dr.David St-Onge 2022. is licensed under a License Creative Commons Attribution - Pas d’utilisation commerciale - Partage dans les mêmes conditions 4.0 International, except where otherwise noted.

Table des matières