9 Perdus dans l’espace ! Localisation et cartographie
Damith Herath
Table des matières
Le point de vue de l’industrie : Guillaume Charland-Arcand
9.3 Problème de localisation des robots
9.3.1 Localisation basée sur l’odométrie
9.3.2 Odométrie basée sur l’IMU
9.4 Le problème de la cartographie des robots
9.4.1 Cartes de grille d’occupation
9.5 Le problème de la localisation et de la cartographie simultanées (SLAM)
9.5.1 Approche théorique de l’estimation des problèmes de localisation, de cartographie et de SLAM
9.6.1 Filtre de Kalman linéaire à temps discret
9.6.2 Le filtre de Kalman étendu (EKF)
9.7 Une étude de cas : Localisation d’un robot à l’aide du filtre de Kalman étendu
9.7.2 Dérivation de l’algorithme de localisation basé sur l’EKF
9.1 Objectifs d’apprentissage
Dans ce chapitre, vous découvrirez :
- Le problème de la localisation des robots
- Le problème de la cartographie des robots
- Le problème de localisation et de cartographie simultanées (SLAM)
- Les techniques courantes d’estimation d’état probabiliste
- Le filtre de Kalman et le rôle du filtre de Kalman étendu (EKF) en tant qu’estimateur d’état récursif dans les systèmes non linéaires
9.2 Introduction
Imaginez que vous visitez une nouvelle ville ou un nouveau pays. Peut-être que comme moi, l’une des premières choses que vous feriez serait de télécharger ou d’imprimer une carte de la région. Ou peut-être vous assureriez-vous que l’application de navigation ou le GPS de votre téléphone est à jour avec la dernière carte de la région ou du pays. Cependant, alors que vous voyagez à travers la région ou la nouvelle ville, vous rappelez-vous des moments où vous vous êtes perdus? Même avec les dernières cartes?
De même, vous êtes-vous déjà demandé comment une voiture autonome sait où elle va?
Une architecture typique d’un système robotique mobile est illustrée dans la Figure 9-1. Elle comprend plusieurs capteurs, modules de planification et de contrôle et des actionneurs. Les blocs de construction sont nécessaires pour un système robotique mobile typique, bien que les instances spécifiques de ces composants dépendent de l’application et de la plate-forme. Tout d’abord, des capteurs internes et externes fournissent des informations sur le robot et le monde physique dans lequel il se déplace. Ensuite, les informations sont interprétées par divers algorithmes pour estimer l’état du robot et son environnement. Cette estimation de l’état utilisée pour planifier les actions du robot et générer des commandes pour les actionneurs. Nous avons examiné les capteurs, les contrôles, la planification de la trajectoire et l’évitement d’obstacles dans les chapitres précédents.
Dans ce chapitre, nous abordons la localisation et la cartographie, qui étaient autrefois considérées comme le Saint Graal de la robotique, et qui sont maintenant deux capacités fondamentales pour tout robot mobile autonome qui doit naviguer dans des environnements naturels, y compris les voitures autonomes (et même les rovers martiens!).
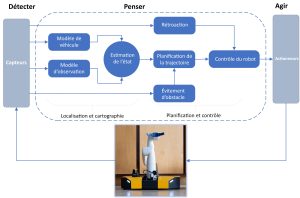
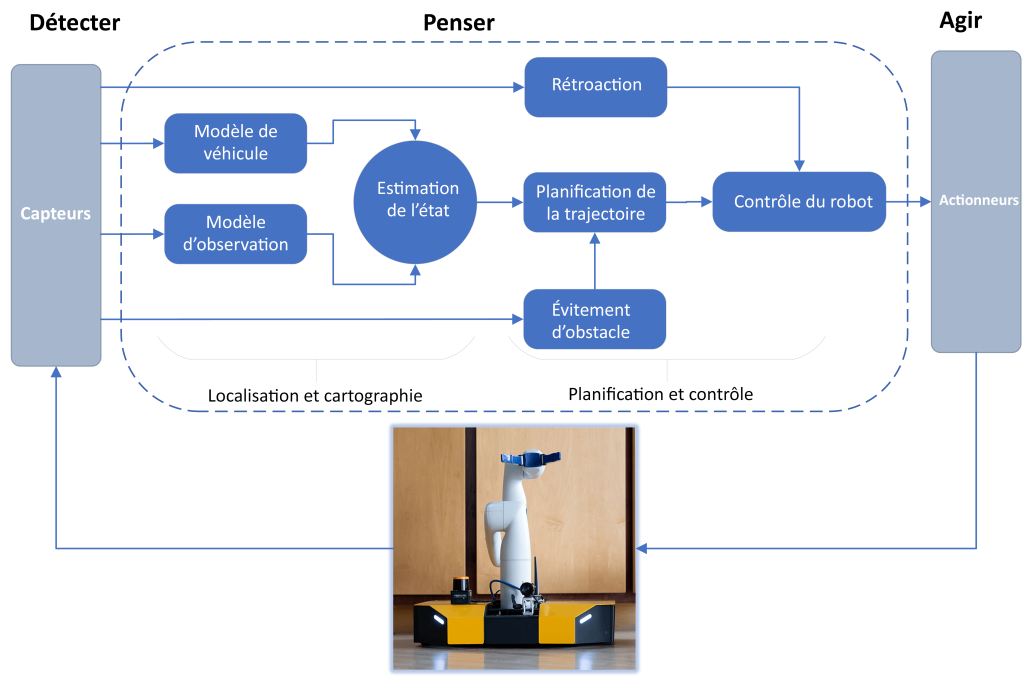
Figure 9-1 : Une vue d’ensemble de haut niveau d’un système robotique mobile avec des capteurs, algorithmes et actionneurs.
Le point de vue de l’industrie : Guillaume Charland-Arcand
Guillaume Charland-Arcand
ARA Robotics
Lors de mes années au CÉGEP, j’ai été initié à la robotique dans un petit club où nous avions construit des robots sumo pour participer à des compétitions. La compétition était assez simple, deux robots s’affrontaient sur un anneau noir circulaire avec une petite barre blanche qui délimitait le bord. L’objectif était de pousser l’autre robot hors de l’anneau. Mon robot était assez rudimentaire avec de gros moteurs, des roues imposantes, quelques capteurs, un microcontrôleur de 8 bits, ma propre carte de circuit imprimé et quelques lignes de code. Bien que je n’ai pas obtenu beaucoup de succès lors de ces compétitions, j’ai trouvé incroyable de pouvoir construire quelque chose de mes propres mains en combinant la mécanique, l’électronique et le logiciel, et de voir le résultat bouger. C’était vraiment cool! Cependant, lorsque j’étais à l’université, je sentais que mes connaissances étaient limitées, donc j’ai décidé de rejoindre un club scientifique axé sur les drones multirotors, qui était assez nouveaux à l’époque. J’ai instantanément été conquis par cette branche de la robotique. Ces robots mobiles étaient comme mon bon vieux robot sumo, mais sous stéroïdes. Tout était plus complexe : il y avait plus de vibrations, une dynamique non linéaire compliquée, une capacité de charge utile limitée et il volait!
Cependant, à l’époque, quand j’ai commencé ma maîtrise, travailler avec des drones était difficile à cause du manque de ressources. J’avais réussi à persuader mon superviseur d’acheter de l’équipement, mais en raison des contraintes budgétaires, nous ne pouvions nous permettre qu’un seul drone. Cela a compliqué les choses pour moi, car une erreur, une ligne de code erronée et le drone s’écrase. Travailler sur la conception des lois de commande a rendu cela encore plus difficile. Toute personne ayant travaillé sur la théorie de la commande a connu cela : sur le papier et dans les simulations, tout semble parfait, mais il y a toujours cette mise en garde selon laquelle trouver les gains du contrôleur nécessite généralement des expérimentations. J’avais un seul drone et le défi était de régler le contrôleur et de valider le logiciel sans qu’il s’écrase. C’est alors que j’ai découvert les pratiques de l’ingénierie critique pour la sécurité, qui impliquent de concevoir systématiquement les logiciels et le matériel pour éviter les pannes. Bien que je n’aie pas suivi les normes DO-178, cela m’a permis de mieux comprendre comment développer des produits et des applications robotiques.
Au début de mon parcours, la technique SLAM commençait à être appliquée aux drones. Bien que quelques progiciels ROS existaient déjà, ils étaient principalement en 2D et utilisaient le télémètre laser à balayage Hokuyo. Il y avait également eu des démonstrations réussies de drones autonomes opérant dans des environnements sans GNSS, mais cela restait principalement des prototypes dans des contextes expérimentaux. Des entreprises comme Exyn Technologies et Skydio proposent aujourd’hui des produits pour des applications industrielles qui ont un niveau d’autonomie très élevé. Ces systèmes permettent de créer des cartes 3D extrêmement précises, de détecter des obstacles statiques et dynamiques, ainsi que de planifier des trajectoires à grande vitesse dans des environnements inconnus. Les avancées technologiques des cinq dernières années ont été significatives et représentent une base solide pour les innovations à venir, car la tâche de l’autonomie est complexe et n’est pas encore totalement résolue.
9.3 Le problème de la localisation des robots
Pour qu’un robot mobile autonome soit déployé avec succès, il faut répondre à la question « où suis-je? ». Par exemple, dans la Figure 9-2 : A robot travelling in a local coordinate frame, un robot est représenté au moment [latex]t=k[/latex] à un endroit inconnu. Le problème de localisation du robot est de déterminer les coordonnées actuelles ainsi que le cap (la direction vers laquelle le robot est orienté) du robot par rapport à un référentiel de coordonnées local donné. Le référentiel de coordonnées local est généralement fixé à l’endroit où se trouvait le robot au moment [latex]t=0[/latex], bien que cela puisse être choisi arbitrairement. Le robot dispose également de ses propres coordonnées. En règle générale, le cap est défini comme l’angle entre l’axe x du référentiel de coordonnées local et l’axe x du référentiel de coordonnées du robot. On dit que le problème de localisation est résolu pour un temps donné [latex]t=k[/latex] quand [latex]x,y,z[/latex] les coordonnées et le cap courant [latex](\psi)[/latex] du robot par rapport au référentiel de coordonnées local donné est entièrement connu.
Dans l’exemple illustré, le robot connaît sa position de départ. Le problème de localisation pourrait alors être considéré comme un problème de suivi, où l’exigence est de suivre le mouvement du robot depuis le début par rapport à sa position initiale. En revanche, si la position initiale n’est pas connue, alors le problème de localisation est considéré comme un problème de positionnement global. Un exemple illustrant ceci pourrait être un robot activé à un endroit aléatoire sans avoir connaissance de sa position initiale.
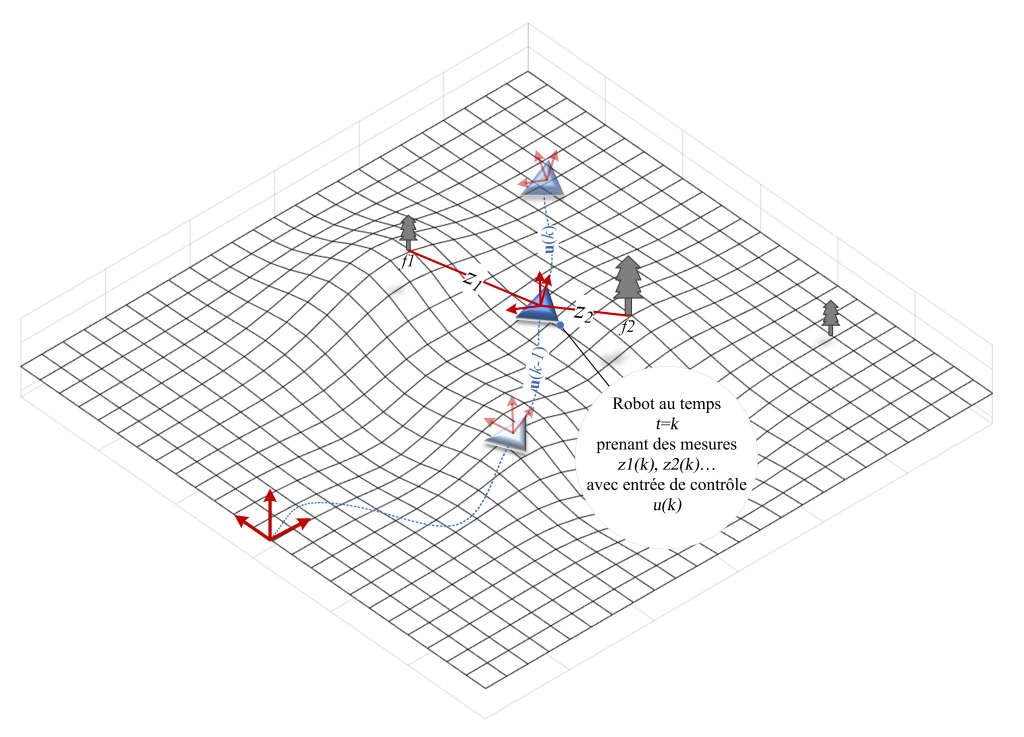
Figure 9-2 : Un robot se déplaçant dans un référentiel de coordonnées local.
Un autre problème connexe est le problème de robot « kidnappé », où un robot correctement localisé est soudainement déplacé vers un endroit différent sans être conscient du mouvement. Un exemple de cette situation, pourrait être un robot aspirateur partant de sa station de charge (référentiel de coordonnées local connu) et soudainement ramassé par un utilisateur et placé dans une autre pièce (qui ferait ça?).
9.3.1 Localisation basée sur l’odométrie
L’une des techniques les plus répandues en robotique pour déterminer l’emplacement actuel d’un robot consiste à utiliser des encodeurs à roue. Odométrie – le mot est dérivé des racines grecques (odos – rue et métro – mesurer), fait simplement référence à toute technique qui utilise des informations de mouvement pour dériver des estimations de position relative du robot. Tout comme l’odomètre présent dans les véhicules, pour mesurer la distance parcourue par le véhicule (soit la distance absolue depuis sa fabrication, soit la distance relative à partir d’un point de départ arbitraire), les encodeurs de roue peuvent être utilisés pour calculer les distances de déplacement relatives ainsi que le cap du robot en se basant sur la géométrie et la dynamique des roues. Ce processus est parfois appelé à l’estime. Cependant, en raison des erreurs de capteur, du glissement et d’autres éléments de bruit inhérents à ces systèmes, l’odométrie accumule des erreurs au fil du temps. Comme représenté sur la Figure 9-3, un robot pourrait perdre la trace de sa position relativement rapidement s’il ne s’appuyait que sur l’odométrie. Néanmoins, l’odométrie est largement utilisée en robotique pour acquérir des informations de localisation à court terme.
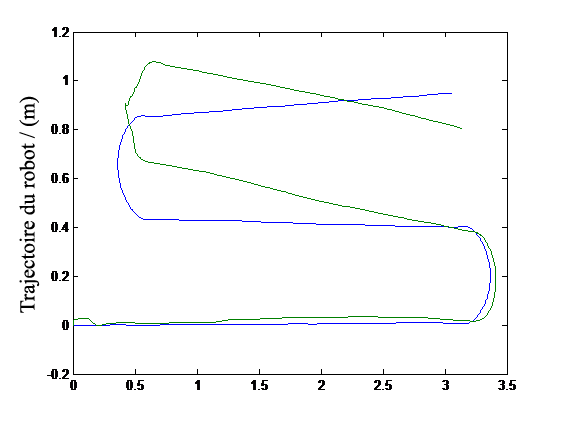
Figure 9-3 : Véritable trajectoire d’un robot (bleu) comparée à l’estimation basée sur l’odométrie de la trajectoire.
9.3.2 Odométrie basée sur l’UMI
Les unités de mesure inertielle (MUI) sont des dispositifs qui intègrent plusieurs capteurs dans un seul boîtier, notamment des accéléromètres et des gyroscopes. Les MUI pourraient être utilisées pour mesurer l’accélération linéaire du robot en 3 dimensions (à l’aide d’un accéléromètre triaxial) et la vitesse de rotation (à l’aide de gyroscopes). En intégrant ces informations de manière appropriée, il est possible de déduire la vitesse et la distance de déplacement du robot, ce qui permet d’élaborer l’emplacement relatif du robot ainsi que les informations de cap. Cependant, les MUI sont susceptibles à la « dérive » où elles accumulent des erreurs au fil du temps.
9.3.3 Odométrie visuelle
L’odométrie visuelle est une technique alternative qui utilise des caméras et la vision par ordinateur pour capturer des informations odométriques. Diverses techniques de vision par ordinateur ont été utilisées pour estimer le mouvement des robots. En général, ces techniques cherchent à comprendre les variations relatives entre les images successives en raison du mouvement. Une approche courante consiste à suivre un ensemble de caractéristiques d’image à travers des trames (voir le chapitre 7). Ces techniques sont parfois couplées à une MUI pour améliorer les estimations. De tels systèmes sont généralement appelés odométrie inertielle visuelle.
9.3.4 Localisation basée sur l’odométrie
Les techniques précédentes décrites pour résoudre le problème de localisation ne fournissent que des informations relatives. En d’autres termes, ces techniques nécessitent l’intégration d’une série de mesures pour déduire la position actuelle du robot. Une autre technique consiste à utiliser une carte externe pour effectuer des observations directes sur une série de repères (aussi appelé balises ou caractéristiques) à l’aide d’un capteur monté sur le robot afin de déduire l’emplacement actuel du robot par rapport à ces repères en fonction d’une carte a-priori. Autrement dit, si vous connaissez les emplacements d’un ensemble de points de repère préalablement identifiés dans l’environnement par rapport à un référentiel de coordonnées global/local (c’est-à-dire qu’une carte locale de l’environnement a déjà été élaborée), et si vous possédez un capteur capable de ré-identifier et mesurer l’emplacement relatif de ces points de repère par rapport à sa position, il est alors possible de localiser votre robot dans le référentiel de coordonnées donné en utilisant la méthode de triangulation. La méthode de triangulation utilise deux emplacements connus pour « trianguler » ou déterminer l’emplacement d’un troisième point à l’aide de la géométrie. Afin de trianguler, les distances et les angles des emplacements connus (points de repère) par rapport à l’emplacement inconnu doivent être mesurés (voir Figure 9-4).
Imaginez un robot observant n des points de repère dans l’environnement avec des emplacements connus à l’aide d’un capteur affecté par le bruit où l’emplacement actuel du robot est inconnu ;
L’emplacement actuel du robot (inconnu) est : [latex]\mathbf{x}_{r}=\left[x_{r}, y_{r}\right][/latex]
Positions mesurées aux points de repère connus : [latex]\boldsymbol{\theta}=\left[\theta_{1}, \theta_{2}, \ldots, \theta_{n}\right]^{\mathrm{T}}[/latex]
Emplacements réels des points de repère (connus) : [latex]\mathbf{x}_{i}=\left[x_{i}, y_{i}\right]^{\mathrm{T}}[/latex]
Positions réelles des points de repère (inconnus) : [latex]\bar{\theta}\left(\mathbf{x}_{r}\right)=\left.\left[\bar{\theta}_{1}\left(\mathbf{x}_{r}\right), \bar{\theta}_{2}\left(\mathbf{x}_{r}\right), \ldots, \bar{\theta}_{n}\left(\mathbf{x}_{r}\right)\right)\right]^{\mathrm{T}}[/latex]
Où, [latex]\tan \bar{\theta}_{i}\left(\mathbf{x}_{r}\right)=\frac{y_{i}-y_{r}}{x_{i}-x_{r}}[/latex]
En supposant que l’erreur de mesure est [latex]\left(\delta \theta_{i}\right)[/latex] nous pouvons élaborer une relation entre la position mesurée et la position actuelle pour chaque caractéristique observée : [latex]\theta_{i}=\bar{\theta}_{i}\left(\mathbf{x}_{r}\right)+\delta {\theta}_{i}[/latex] ou :
| [latex]\boldsymbol{\theta}=\bar{\theta}\left(\mathbf{x}_{r}\right)+\delta \theta[/latex] | (9.1) |
Où :
| [latex]\delta \theta=\left[\delta \theta_{1}, \delta \theta_{2}, \ldots, \delta \theta_{n}\right]^{\mathrm{T}}[/latex] | (9.2) |
et en supposant que la mesure de bruit est gaussienne à moyenne nulle et indépendante, la matrice de covariance sera déterminée par :
| [latex]\Sigma=\operatorname{diag}\left(\sigma_{1}^{2}, \sigma_{2}^{2}, \ldots, \sigma_{n}^{2}\right)[/latex] | (9.3) |
Nous pouvons alors concevoir l’estimateur de vraisemblance maximale de l’emplacement du robot :
| [latex]\hat{\boldsymbol{x}}_{r}=\operatorname{argmin} \frac{1}{2}\left[\bar{\theta}\left(\hat{\boldsymbol{x}}_{r}\right)-\boldsymbol{\theta}\right]^{\mathrm{T}} \Sigma^{-1}\left[\bar{\theta}\left(\hat{\boldsymbol{x}}_{r}\right)-\boldsymbol{\theta}\right][/latex] | (9.4) |
On peut désormais résoudre ce problème de manière récursive en utilisant une technique telle que l’algorithme de Gauss-Newton comme un problème des moindres carrés non linéaires.
Les algorithmes de localisation les plus courants supposent que les points de repère sont stationnaires pendant tout le déplacement du robot. C’est ce qu’on appelle l’hypothèse de l’environnement statique. Un environnement est considéré comme dynamique s’il contient des éléments cartographiques (à l’exception du robot) qui se déplacent, tels que des humains, des véhicules et d’autres robots. Bien évidemment, de tels éléments dynamiques ne conviennent pas comme repères de localisation et sont traités comme du bruit. En robotique, ces repères peuvent être des caractéristiques visuellement saillantes qui apparaissent naturellement dans l’environnement donné (par exemple, les coins et les bords), ou bien ils peuvent être placés artificiellement (par exemple, les balises laser rétroréfléchissantes). Un capteur approprié (par exemple une caméra et un télémètre laser) ainsi que des techniques de traitement du signal appropriées doivent être utilisés pour détecter et mesurer la distance et l’angle (position) à ces caractéristiques par rapport au référentiel de coordonnées du capteur.
Le GPS (Système de positionnement global) utilise les informations de distance entre le robot et le satellite (via le temps de vol et les données spécifiques au satellite) pour localiser, en utilisant une légère variation de la technique de triangulation appelée trilatération ce qui nécessite de connaître uniquement les distances aux repères (ou aux satellites). Pour améliorer la précision de l’estimation de l’emplacement, il est préférable d’avoir plus de deux points de repère. Cela est également vrai pour le scénario de triangulation décrit précédemment.
Un problème connexe appelé association de données traite de la désambiguïsation des caractéristiques détectées et de l’association correcte avec les caractéristiques cartographiques connues. Ce problème ne se pose pas avec le GPS, car chaque satellite de la constellation envoie des informations identifiables de manière unique au récepteur.
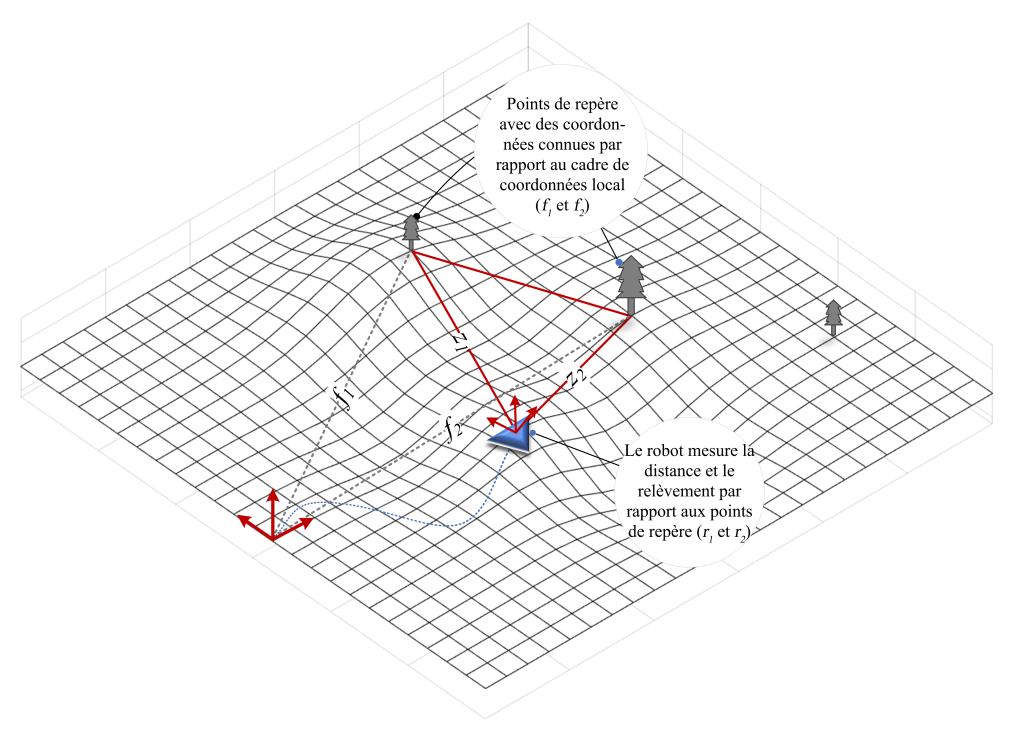
Figure 9-4 : Localisation basée sur la carte.
9.4 Problème de cartographie du robot
Dans la section précédente, nous avons expliqué comment les objets de l’environnement du robot pouvaient être utilisés pour localiser le robot. La disponibilité des cartes était particulièrement intéressante. Comment ces cartes sont-elles générées? La Figure 9-5 montre une ancienne carte de Taprobana, l’actuel Sri Lanka, dessinée par l’ancien mathématicien et cartographe Claudius Ptolémée. Les coordonnées géographiques utilisées pour dessiner la carte ont été dérivées d’outils et de techniques disponibles à l’époque. Aujourd’hui, ces cartes sont dessinées à l’aide de techniques d’arpentage modernes utilisant des outils modernes et des données de localisation GPS. L’idée générale reste cependant la même. Les mesures sont effectuées sur les caractéristiques d’intérêt (par exemple, les contours, les arbres, les structures) et sont tracées par rapport à un référentiel de coordonnées fixe. Comme vous le remarquerez, la carte de Ptolémée n’a qu’une ressemblance passagère avec les cartes actuelles du pays. Dans les temps anciens, avant l’invention du GPS pour la géolocalisation, les marins et les cartographes utilisaient l’observation du soleil et des étoiles à l’aide d’instruments tels que le sextant pour se repérer, ce qui conduisait à d’importantes erreurs de mesure et de localisation. Pour créer des cartes précises à cette époque, il était nécessaire de mesurer avec précision les caractéristiques de référence et d’être capable de localiser l’instrument de mesure avec précision dans le référentiel de coordonnées.
Lors du déploiement de robots, il est possible d’accéder à des cartes à priori à de nombreuses reprises. Par exemple, dans les structures intérieures, il peut être possible de se référer aux plans dessinés par l’architecte du bâtiment ou de placer des balises artificielles (par exemple des marqueurs rétroréfléchissants qui répondent à la lumière laser) à des emplacements connus et fixes. Cependant, cela suppose que la structure n’a pas été modifiée par rapport aux plans d’origine, qui peuvent ne pas être précis et pour les grands environnements, le placement et la mesure des balises artificielles deviennent une proposition fastidieuse. De plus, il y a des éléments semi-permanents dans le bâtiment, tels que des meubles, qui changeront d’emplacement au fil du temps, augmentant la nature transitoire des cartes. Il est également possible que le robot doive être déployé dans un environnement où aucune carte pré-définie n’existe. Dans une telle situation, le robot doit créer sa propre carte. Alors que le problème de localisation est relativement plus facile à résoudre en raison de sa nature de faible dimension, le problème de création d’une carte est beaucoup plus difficile, surtout si l’environnement est vaste.
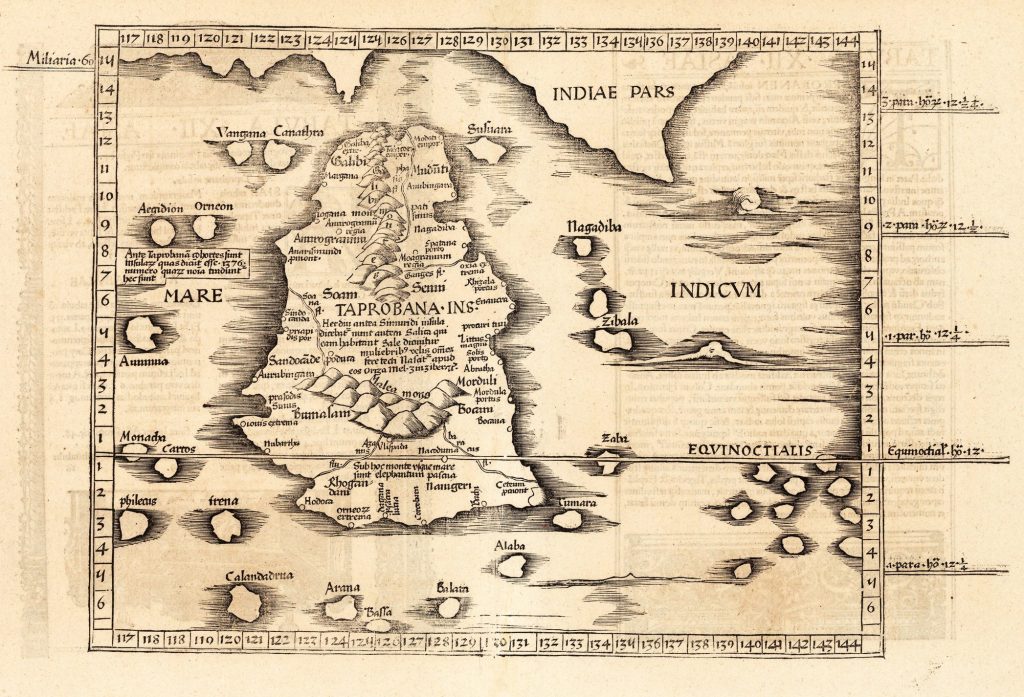
Figure 9-5 : Taprobana de Ptolémée, publié dans Cosmographia Claudii Ptolomaei Alexandrini, 1535 (Sri Lanka actuel) (Bailey and Durrant-Whyte, 2006)
9.4.1 Cartes à quadrillage d’occupation
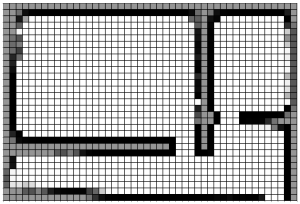
L’une des techniques les plus simples utilisées en robotique pour créer une carte est la carte à quadrillage d’occupation. Une méthode fréquemment utilisée en cartographie 2D pour décrire la disposition spatiale de l’environnement d’un robot consiste à utiliser des cartes à quadrillage d’occupation, qui découpent le plan d’étage en une grille de cellules. La Figure 9-6 montre une petite carte à quadrillage d’occupation d’un environnement intérieur. Les nuances grises indiquent où le capteur (un télémètre laser dans ce cas) a détecté des obstacles. Les zones moins denses de la « carte » indiquent une moindre certitude d’un obstacle à ces endroits. La ligne bleue indique la trajectoire du robot pendant l’exercice de cartographie. Si vous vous demandez comment la trajectoire du robot a été générée, sachez que nous avons utilisé un algorithme de localisation qui s’est appuyé sur des balises laser placées à des endroits connus dans l’environnement. Si nous avions utilisé les données odométriques pour générer la carte à quadrillage d’occupation, les résultats auraient été aussi mauvais que la carte de Ptolémée.
 |
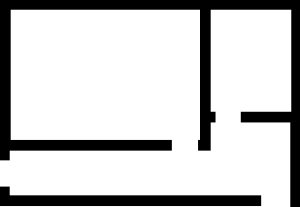 |
Figure 9-6 : Une carte à quadrillage d’occupation (à gauche) et le plan réel de la zone cartographiée (à droite) (crédit image : Rafael Gomes Braga)
9.4.2 Autres types de cartes
Les cartes qui représentent l’environnement en utilisant une représentation géométrique, comme les Figure 9-6, sont appelées cartes métriques. D’autres types de cartes incluent les cartes de caractéristiques qui représentent l’environnement à l’aide d’un ensemble de caractéristiques saillantes telles que les bords et les coins; les cartes sémantiques qui combinent des informations géométriques avec des informations sémantiques de haut niveau telles que des objets identifiables par des humains dans l’environnement (par exemple des livres, des tableaux) et leur relation les uns avec les autres. Les cartes métriques et de caractéristiques sont relativement moins intuitives pour les humains. Les cartes sémantiques fournissent un environnement plus riche en données que les humains peuvent interpréter. Ces cartes sont utiles lorsque les humains et les robots doivent interagir. Par exemple, une implémentation de carte sémantique est mieux adaptée dans une situation de voiture autonome, alors qu’une carte métrique pourrait être plus efficace pour une application minière souterraine.
9.5 Le problème de localisation et de cartographie simultanées (SLAM)
Si le robot dispose d’une carte préalablement établie, il peut être localisé dans l’environnement, comme dans notre exemple en début de chapitre où l’on visite une nouvelle ville avec une carte. De manière inverse, si la position du robot est connue, il est possible d’établir une carte de l’environnement, à l’instar des géomètres qui créent de nouvelles cartes à partir d’informations de localisation GPS. Mais, que se passe-t-il si le robot n’a pas de carte et ne connaît pas l’emplacement? C’est le redoutable problème de la poule et de l’œuf en robotique. La question est de savoir comment créer une carte tout en utilisant la même carte pour localiser simultanément. Le problème est communément connu sous le nom de « problème de localisation et de cartographie simultanées (SLAM) ». À la fin des années 90, il a été démontré qu’il est en effet possible pour un robot de partir d’un emplacement inconnu dans un environnement inconnu pour créer progressivement une carte de l’environnement tout en calculant simultanément la position du robot à l’aide de la carte en cours de création.
9.5.1 Une approche théorique d’estimation des problèmes de localisation de cartographie et de SLAM.
Cependant, comme nous l’avons vu dans les chapitres précédents, les capteurs utilisés dans un robot peuvent être des capteurs affectés par le bruit et l’environnement peut être imprévisible, ce qui entraîne des incertitudes inhérentes aux mesures effectuées sur l’environnement. Par conséquent, il est nécessaire de considérer ces incertitudes dans toute formulation canonique du problème.
Afin de tenir compte des incertitudes sous-jacentes du système, il est possible d’explorer une classe d’algorithmes qui modélisent explicitement l’incertitude du système à l’aide de théories des probabilités. Ainsi, le problème de localisation, de cartographie ou de SLAM pourrait être formulé comme un problème d’état d’estimation multivarié avec mesures affectées par du bruit :
| [latex]\hat{\mathbf{x}}_{\mathrm{MAP}} \triangleq \operatorname{argmax} ~ \mathbf{x}p(\mathbf{z})[/latex] | (9.5) |
Où [latex]\mathbf{x}[/latex] représente la variable d’état et [latex]\mathbf{z}[/latex] représente le vecteur de mesure. Nous supposons que chaque état multivarié est une distribution normale.
Si nous pouvons en outre supposer qu’une distribution antérieure p sur [latex]\mathbf{x}[/latex] existe, alors le problème ci-dessus pourrait être reformulé en utilisant le théorème de Bayes (voir chapitre 6) :
| [latex]\hat{\mathbf{x}}_{\mathrm{MAP}} \triangleq \operatorname{argmax} ~ \mathbf{x}p(\mathbf{x}) p(\mathbf{x})[/latex] | (9.6) |
Ici, [latex]p(\mathbf{z}|\mathbf{x})[/latex] est la vraisemblance de la mesure et [latex]p( \mathbf{x})[/latex]est l’antérieure. On formule le problème de manière à ce qu’il puisse être résolu de manière récursive, comme cela a été fait avec le problème de triangulation simple mentionné précédemment. Nous pouvons maintenant estimer les états du robot et de la carte à plusieurs reprises à partir d’un point de départ donné. Pour ce faire, nous devons d’abord définir les vecteurs d’état pertinents du robot et de l’environnement,
L’état du robot pour un robot mobile fonctionnant en 2D pourrait être exprimé comme suit :
| [latex]\mathbf{x}_{r}=\begin{bmatrix} x_{r} \\ y_{r} \\ \phi_{r}\end{bmatrix}[/latex] | (9.7) |
où [latex]x_{r}[/latex] et [latex]y_{r}[/latex] désignent l’emplacement actuel de l’origine du référentiel de coordonnées du robot par rapport au référentiel de coordonnées local et [latex]\phi _{r}[/latex] est le cap du robot par rapport à l’axe x du référentiel de coordonnées du robot.
En supposant que notre carte doit être créée à l’aide d’une carte de caractéristiques métriques, l’emplacement de [latex]i^{th}[/latex] des caractéristiques cartographique peut être défini comme le vecteur,
| [latex]\mathbf{x}_{f i}=\begin{bmatrix} x_{i} \\ y_{i} \\ z_{i} \end{bmatrix}[/latex] | (9.8) |
Où [latex]\left(x_{i}, y_{i}, z_{i}\right)[/latex] sont les coordonnées 3D des [latex]i^{th}[/latex] caractéristiques par rapport au référentiel de coordonnées local. Si l’on suppose que l’ensemble de la carte de l’environnement constituera une [latex]n[/latex] nombre de ces caractéristiques, alors le vecteur de la carte pourrait être défini comme :
| [latex]\mathbf{x}_{m}=\begin{bmatrix} \boldsymbol{x}_{f 1} \\ \vdots \\ \boldsymbol{x}_{f n} \end{bmatrix}[/latex] | (9.9) |
Ensuite, selon le problème spécifique, nous pouvons assembler le vecteur d’état [latex]\mathbf{x}[/latex] à estimer pour un temps donné [latex]t=k[/latex], comme suit :
- Pour le problème de localisation,
| [latex]\mathbf{x}(k)=\left[\mathbf{x}_{r}(k)\right][/latex] | (9.10) |
- Pour le problème de cartographie,
| [latex]\mathbf{x}(k)=\left[\mathbf{x}_{m}(k)\right][/latex] | (9.11) |
- Pour le problème de localisation et de cartographie simultanées,
| [latex]\mathbf{x}(k)=\begin{bmatrix} \mathbf{x}_{r}(k) \\ \mathbf{x}_{m}(k) \end{bmatrix}[/latex] | (9.12) |
Une fois le vecteur d’état défini, le processus d’estimation se déroule en trois étapes à une étape de temps donné [latex]t=k[/latex] (voir Figure 9-8):
1. Étape de prédictionDans l’étape de prédiction, nous utiliserons un modèle de mouvement du robot (entrée de contrôle) pour prédire comment les états du robot évolueraient sur l’étape de temps considéré.
2. Étape d’observationÀ ce stade, le robot utilise ses capteurs embarqués pour effectuer des mesures sur les éléments cartographiques de l’environnement. Les caractéristiques saillantes de l’environnement peuvent être détectées à l’aide d’une caméra de profondeur et d’un algorithme de vision par ordinateur, permettant ainsi de mesurer leur emplacement par rapport au référentiel de coordonnées du robot. Il est essentiel de souligner que les algorithmes utilisés doivent être capables de reconnaître les caractéristiques plusieurs fois et de les faire correspondre correctement dans le temps, ce qui signifie que les caractéristiques nouvellement observées doivent être correctement appariées aux caractéristiques déjà présentes sur la carte. Cette capacité à faire correspondre les observations aux éléments cartographiques correspondants est appelée association de données (Figure 9-7). Bien sûr, si une caractéristique observée n’est pas déjà sur la carte, une telle caractéristique devra être initialisée d’abord (c’est-à-dire ajouté au vecteur de carte).

Figure 9-7 : Un algorithme de vision utilisé pour détecter les caractéristiques saillantes de l’environnement. Les images du haut et du bas montrent deux vues du même environnement capturées à deux intervalles de temps différents du parcours du robot. Les lignes indiquent les caractéristiques appariées entre les deux images (association de données). Pouvez-vous repérer des instances d’association de données ayant échouées?
Ces mesures sont intrinsèquement affectées par le bruit en raison de leur nature physique et des limitations des algorithmes. Les estimations des états basées sur ces entrées de capteur sont donc limitées par la précision des capteurs utilisés pour les observations. Cependant, lors de la dernière étape du processus d’estimation, ce bruit sera filtré.
3. Étape de mise à jour
Au cours de l’étape de mise à jour, les informations de prédiction et les observations sont combinées pour produire une meilleure estimation des états. Le processus pourrait être représenté comme suit :
| [latex]\widehat{x}=\left( 1-w\right) \mathbf{x}_{prédit}+w\mathbf{x}_{observé}[/latex] | (9.13) |
Où w est un facteur de pondération utilisé pour déterminer l’importance relative de l’observation et de la prédiction. Si les capteurs utilisés dans le robot fournissent des mesures d’observation très précises, ce paramètre sera réglé plus près de 1. Si les capteurs sont plus bruyants et que vous devez vous fier aux prédictions, cette valeur doit être définie plus près de 0. Afin de sélectionner la meilleure valeur pour le facteur de pondération, il est important de comprendre la nature de vos mesures d’observation (appelées modèle de capteur) et le modèle de mouvement du robot (appelé modèle de véhicule ou modèle de contrôle). Supposons que ce n’est pas correctement « réglé » sur le système. Dans ce cas, les estimations pourraient être soit conservatrices, auquel cas les estimations de l’état comporteront de grandes incertitudes ou optimistes, auquel cas elles confient trop dans les estimations de l’état, là où elles ne sont pas justifiées. L’un ou l’autre scénario conduit à des estimations d’état qui ne sont pas utiles dans le pire des cas, carrément dangereuses. Un exemple de ce dernier pourrait être observé lors de l’utilisation de systèmes GPS pour la localisation dans des environnements densément construits, comme le passage par un chemin étroit au milieu de grands immeubles. Dans ce cas, vous pourriez remarquer que votre estimation de position GPS commence soudainement à sauter et semble parfois se trouver à l’intérieur des bâtiments. Cependant, cela peut toujours indiquer une confiance élevée dans l’estimation, généralement indiquée par un cercle ou une ellipse autour de l’emplacement estimé – plus le cercle est petit, plus la confiance est élevée. Cela se produit en raison du problème inhérent de chemins multiples avec les signaux GPS. Les signaux GPS rebondissent sur les hautes structures avant d’atteindre le récepteur GPS, ce qui entraîne de grandes erreurs dans les calculs de temps de vol. Étant donné que les algorithmes intégrés ne sont pas conscients de ce qui se passe à l’extérieur, ils continuent de faire confiance aux observations conduisant à ces estimations d’état erronées. Pour une voiture autonome ou un robot similaire, cela pourrait être catastrophique, c’est le moins qu’on puisse dire!
Plusieurs algorithmes ont été proposés pour résoudre le problème d’estimation d’état multivarié. L’un des algorithmes les plus populaires est le filtre de Kalman.

Figure 9-8 : Des états inconnus pourraient être estimés de manière récursive à l’aide d’informations de capteur dans un cadre Bayésien.
9.6 Filtre de Kalman
Le filtre de Kalman est une méthode statistique linéaire récursive utilisée pour estimer les états d’intérêt. Pour des systèmes linéaires, le filtre de Kalman de base peut être appliqué, tandis que pour des systèmes non linéaires, le filtre de Kalman étendu (EKF) est utilisé pour une approximation linéaire. Le filtre de Kalman est fréquemment utilisé dans de nombreuses applications. Par exemple, dans la navigation robotique et la fusion de données, le filtre de Kalman est l’une des méthodes fréquemment discutées dans la littérature avec de nombreuses adaptations et modifications.
9.6.1 Filtre de Kalman linéaire à temps discret
Pour un système linéaire soumis à une mesure moyenne nulle gaussienne, non corrélée, et à des bruits de processus, le filtre de Kalman est l’estimateur optimal de l’erreur quadratique moyenne minimale. Pour dériver le filtre d’un tel système, son modèle et le modèle de l’observation doivent être définis. Ensuite, le problème peut être énoncé comme un estimateur linéaire récursif avec des gains inconnus. Les gains peuvent être déterminés à l’aide du critère minimum du carré moyen de l’erreur.
Le filtre de Kalman se compose des trois mêmes étapes récursives décrites dans la section précédente.
- Étape de prédiction
- Étape d’observation
- Étape de mise à jour
Pour un système linéaire à temps discret, l’équation de transition d’état peut s’écrire comme suit :
| [latex]\mathbf{x}(k)=\mathbf{F}(k) \mathbf{x}(k-1)+\mathbf{B}(k)\mathbf{u}(k) + \mathbf{G}(k)\mathbf{v}(k)[/latex] | (9.14) |
où :
- [latex]\mathbf{x}\left( k\right)[/latex] état au moment k
- [latex]\mathbf{u}\left( k\right)[/latex] vecteur de contrôle d’entrée au moment k
- [latex]\mathbf{v}\left( k\right)[/latex] bruit de mouvement additif
- [latex]\mathbf{B}\left( k\right)[/latex] matrice de contrôle de transition d’entrée
- [latex]\mathbf{G}\left( k\right)[/latex] matrice de transition de bruit
- [latex]\mathbf{F}\left( k\right)[/latex] matrice de transition d’état
Et l’équation de mesure linéaire peut s’écrire comme suit :
| [latex]\mathbf{z}(k)=\mathbf{H}(k) \mathbf{x}(k)+\mathbf{w}(k)[/latex] | (9.15) |
où :
- [latex]\mathbf{z}\left( k\right)[/latex] observation faite au moment k
- [latex]\mathbf{x}\left( k\right)[/latex] état au moment k
- [latex]\mathbf{H}\left( k\right)[/latex] modèle de mesure
- [latex]\mathbf{w}\left( k\right)[/latex] bruit d’observation additif
Comme mentionné précédemment, le bruit du système et de la mesure est supposé être de moyenne zéro et indépendant. Ainsi :
| [latex]E[\mathbf{v}(k)]=E[\mathbf{w}(k)]=\mathbf{0}, \forall \mathrm{k}[/latex] | (9.16) |
Et,
| [latex]\mathrm{E}\left[\mathbf{v}(i) \boldsymbol{w}^{T}(j)\right]=0, \forall i, j[/latex] | (9.17) |
Le mouvement et les mesures affectés par le bruit auront la covariance correspondante suivante :
| [latex]\mathrm{E}\left[\mathbf{v}(i) \boldsymbol{v}^{T}(j)\right]=\delta_{i j} \mathbf{Q}(i), \mathrm{E}\left[\mathbf{w}(i) \boldsymbol{w}^{T}(j)\right]=\delta_{i j} R(i)[/latex] | (9.18) |
L’estimation de l’état à la fois à l’étape de temps k, en fonction de toutes les informations jusqu’au moment k s’écrit comme [latex]\hat{\boldsymbol{x}}(k \mid k)[/latex] et l’estimation de l’état à l’étape de temps k, en fonction des informations jusqu’au moment [latex]k-1[/latex] s’écrit comme [latex]\hat{\boldsymbol{x}}(k \mid k-1)[/latex] et s’appelle la prédiction. Ainsi, compte tenu de l’estimation à la [latex](k-1)[/latex]e étape de temps, l’équation de prédiction de l’état à la ke étape de temps peut s’écrire :
| [latex]\hat{\boldsymbol{x}}(k / k-1)=\mathbf{F}(k) \hat{\boldsymbol{x}}(k-1 \mid k-1)+\mathbf{B}(k) \mathbf{u}(k)[/latex] | (9.19) |
Et la prédiction de covariance correspondante :
| [latex]\mathbf{P}(k \mid k-1)=\mathbf{F}(k) \mathbf{P}(k-1 \mid k-1) \mathbf{F}^{T}(k)+\mathbf{G}(k) \mathbf{Q}(k) \mathbf{G}^{T}(k)[/latex] | (9.20) |
Alors l’estimation linéaire sans biais est :
| [latex]\hat{\mathbf{x}}(k \mid k)=\hat{\mathbf{x}}(k \mid k-1)+\mathbf{W}(k)[\mathbf{z}(k)-\mathbf{H}(k) \hat{\mathbf{x}}(k \mid k-1)][/latex] | (9.21) |
Veuillez noter que l’erreur attendue conditionnelle entre l’estimation et l’état réel est zéro.
[latex]\mathbf{W}\left( k\right)[/latex] s’appelle le Gain de Kalman à l’étape de temps k. Ceci est calculé comme suit :
| [latex]\mathbf{W}(k)=\mathbf{P}(k \mid k-1) \mathbf{H}^{T}(k) \mathbf{S}^{-1}(k)[/latex] | (9.22) |
Où [latex]\mathbf{S}\left( k\right)[/latex] est appelée variance d’innovation à l’étape de temps k et donnée par :
| [latex]\mathbf{S}(k)=\mathbf{H}(k) \mathbf{P}(k \mid k-1) \mathbf{H}^{T}(k)+\mathbf{R}(k)[/latex] | (9.23) |
et l’estimation de la covariance est :
| [latex]\mathbf{P}(k \mid k)=(\mathbf{I}-\mathbf{W}(k) \mathbf{H}(k)) \mathbf{P}(k \mid k-1)(\mathbf{I}-\mathbf{W}(k) \mathbf{H}(k))^{T}+\mathbf{W}(k) \mathbf{R}(k) \mathbf{W}^{T}(k)[/latex] | (9.24) |
Essentiellement, le filtre de Kalman prend une moyenne pondérée de la prédiction [latex]\hat{\mathbf{x}}(k \mid k-1)[/latex], sur la base de l’estimation précédente [latex]\hat{\mathbf{x}}(k-1 \mid k-1)[/latex], et une nouvelle observation [latex]\mathbf{z}(k)[/latex] pour estimer l’état d’intérêt [latex]\hat{\mathbf{x}}(k \mid k)[/latex].
Étude de cas : Nous pouvons illustrer ce processus avec un simple exemple d’un jouet 1-D (Figure 9-9). Supposons que le robot ne puisse se déplacer que dans une seule direction [latex](x)[/latex]. Au moment [latex]t=k-1[/latex] le robot est à l’emplacement [latex]x(k-1)[/latex]. Bien que le robot ne connaisse pas cette valeur exacte, il dispose d’une estimation de sa position, donnée par [latex]\mathbf{x}(k-1| k-1)[/latex]. Comme il s’agit d’une estimation de la valeur réelle, son emplacement est incertain, représenté par la courbe au-dessus de lui – la dispersion indiquant l’étendue de l’incertitude. Maintenant, le robot avance vers l’emplacement [latex]\mathbf{x}(k)[/latex] au moment [latex]t=k[/latex] à l’aide d’une entrée de commande [latex]\mathbf{u}(k)[/latex]. En utilisant ces informations, le robot peut maintenant prédire sa position à la nouvelle étape de temps comme [latex]\hat{\mathbf{x}}(k|k-1)[/latex]. Cependant, cela conduit à une erreur accrue dans l’emplacement estimé tel que représenté par la nouvelle courbe. À ce stade, le robot observe un repère (représenté par l’étoile) à l’aide de son capteur embarqué. Supposons que la position exacte de l’étoile, [latex]x_{star}[/latex] est connue du robot (c’est-à-dire qu’une carte est disponible). Le robot mesure la distance [latex]\mathbf{z}(k)[/latex] entre l’étoile et sa position actuelle à l’aide d’un capteur interne. Comme nous disposons maintenant d’une information supplémentaire sur l’emplacement du robot au moment [latex]t=k[/latex], il est possible d’intégrer les nouvelles informations pour arriver à une meilleure estimation de l’emplacement actuel. Si nous faisons confiance au capteur qui a effectué la mesure de distance, nous pourrions peser davantage cette information. La dérivation précédente du filtre de Kalman nous aide à prendre cette décision et à intégrer les nouvelles informations du capteur pondérées par la « confiance » que nous accordons au capteur. Enfin, une meilleure estimation de l’emplacement pourrait être élaborée comme [latex]\hat{\mathbf{x}}(k|k)[/latex]résultant en une réduction de l’incertitude de l’emplacement du robot. Cette nouvelle estimation pourrait alors être utilisée pour prédire l’emplacement du robot à [latex]t=k+1[/latex] et le processus pourrait être répété.
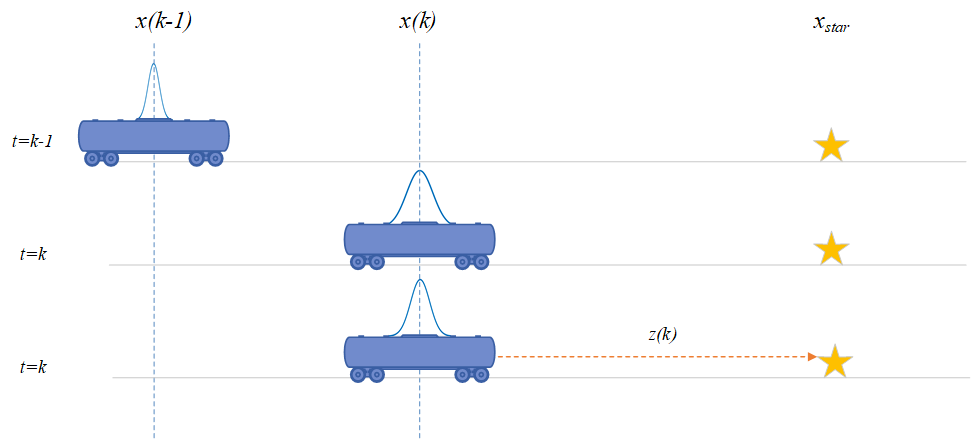
Figure 9-9 : Un exemple de localisation de robot 1-D
9.6.2 Le filtre de Kalman étendu (EKF)
Bien que le filtre de Kalman soit l’estimateur optimal de l’erreur quadratique moyenne minimale pour un système linéaire, les robots actuels sont non linéaires. Le filtre de Kalman étendu (EKF) a été proposé pour remédier à ce problème en utilisant une approximation linéaire des modèles non linéaires. Cependant, il est important de prendre en compte les limitations de l’approximation linéaire pour les fonctions non linéaires et si cette dernière est correctement traitée, l’EKF peut fournir de très bons résultats dans de nombreuses applications. L’algorithme du filtre de Kalman étendu est très similaire à l’algorithme de filtre de Kalman linéaire avec les substitutions :
| [latex]\mathbf{F}(k) \rightarrow \nabla \mathbf{f}_{\mathbf{X}}(k) \text { et } \boldsymbol{H}(k) \rightarrow \nabla \mathbf{h}_{\mathbf{X}}(k)[/latex]Où [latex]\nabla \mathbf{f}_{\mathbf{X}}(k)[/latex] | (9.25) |
et [latex]\nabla \mathbf{h}_{\mathbf{X}}(k)[/latex] sont des fonctions non linéaires d’état et d’étape de temps. Celles-ci sont appelées les jacobiennes, ou les dérivées partielles des fonctions de transition d’état et de mesure, respectivement (voir le chapitre 6). Ceci implique que ces fonctions sont différentiables.
Ensuite, les principales équations peuvent être résumées comme suit ;
1. Équations de prédiction :
| [latex]\hat{\mathbf{x}}(k / k-1)=\mathbf{f}((k-1 \mid k-1), \mathbf{u}(k))[/latex] | (9.26) |
| [latex]{P}(k \mid k-1)=\nabla \mathbf{f}_{\mathbf{X}}(k) \mathbf{P}(k-1 \mid k-1) \nabla^{T} \mathbf{f}_{\mathbf{X}}(k)+\mathbf{Q}(k)[/latex] | (9.27) |
2. Mettre à jour les équations :
| [latex]\hat{\mathbf{x}}((k \mid k)=\hat{\mathbf{x}}(k \mid k-1)+\mathbf{W}(k)[\mathbf{z}(k)-\mathbf{h}(\hat{\mathbf{x}}(k \mid k-1))][/latex] | (9.28) |
| [latex]\mathbf{P}(k \mid k)=\mathbf{P}(k \mid k-1)-\mathbf{W}(k) \mathbf{S}(k) \mathbf{W}^{T}(k)[/latex] | (9.29) |
Où,
| [latex]\mathbf{S}(k)=\nabla \mathbf{h}_{\mathbf{X}}(k) \mathbf{P}(k \mid k-1) \nabla^{T} \mathbf{h}_{\mathbf{X}}(k)+\mathbf{R}(k)[/latex] | (9.30) |
9.6.3 Association de données
L’un des problèmes rencontrés lors de la fusion de données dans un scénario de navigation robotique consiste à identifier les observations des capteurs avec les objets observés. Comme mentionné précédemment, ce problème est couramment appelé le problème d’association de données. Il existe plusieurs méthodes pour discerner les observations. La méthode la plus évidente consiste à faire en sorte que les observations s’auto-identifient. Un exemple de cela a été présenté précédemment en utilisant la vision par ordinateur, où un algorithme d’appariement de caractéristiques est utilisé pour l’association de données.
Des méthodes statistiques sont également disponibles pour déterminer la probabilité qu’une observation donnée appartienne à l’objet que l’on pense observer. Une dérivation des équations pour une telle méthode appelée distance Mahalanobis est discutée ci-dessous.
La différence entre l’observation observée et l’observation prédite pour un ensemble de données de capteur est appelée l’innovation ([latex]\boldsymbol{v}[/latex]) et pourrait être représentée avec les notations introduites précédemment dans la section filtre de Kalman comme suit :
| [latex]\boldsymbol{v}(k)=\mathbf{z}(k)-\hat{\mathbf{z}}(k \mid k-1)[/latex] | (9.31) |
où [latex]\hat{\mathbf{z}}((k \mid k-1)[/latex] est l’observation prédite pour l’étape de temps k étant donné les informations d’observation jusqu’à l’étape de temps [latex]k-1[/latex]. On peut prouver que l’innovation est blanche avec une moyenne de zéro et une variance [latex]\mathbf{S}(k)[/latex] donnée ci-après :
| [latex]\mathbf{S}(k)=\mathbf{R}(k)+\mathbf{H}(k) \mathbf{P}(k \mid k-1) \mathbf{H}^{T}(k)[/latex] | (9.32) |
Les informations ci-dessus peuvent ensuite être utilisées dans le problème d’association de données. L’innovation normalisée au carré [latex]\mathbf{q}(k)[/latex] est défini comme :
| [latex]\mathbf{q}(k)=\boldsymbol{v}^{\boldsymbol{T}}(k) \mathbf{S}^{-1} \boldsymbol{v}(k)[/latex] | (9.33) |
Si le filtre associé est supposé être cohérent, l’équation ci-dessus peut être montrée comme étant une [latex]χ^2[/latex] distribution aléatoire avec [latex]m[/latex] degrés de liberté, où [latex]m = dim(z(k))[/latex], qui représente la dimension de la séquence d’observation.
Une valeur de confiance peut être choisie parmi les tableaux [latex]x^2[/latex] et comparée à la valeur de [latex]\mathbf{q}[/latex] pour chaque observation dans la séquence d’observation. Si la valeur de [latex]\mathbf{q}[/latex] pour une observation donnée est inférieure au seuil, alors cette observation est susceptible d’être associée à l’objet d’observation correct. Si plusieurs observations satisfont à la condition ci-dessus, il est plus sûr d’ignorer ces observations, car une association de données incorrecte pourrait entraîner des performances de filtre instables.
9.7 Une étude de cas : Localisation de robots à l’aide du filtre de Kalman étendu
Abordons maintenant une application concrète du filtre de Kalman étendu pour résoudre le problème de localisation.
9.7.1 Hypothèses
Il est crucial de prendre en compte correctement le modèle de mouvement utilisé, car cela influence grandement le choix du filtre et des capteurs à utiliser pour assurer le succès de l’opération. Par conséquent, il doit être correctement pris en compte avec le choix des capteurs. L’algorithme utilisé dans cette étude de cas utilise les contraintes de corps rigide et de mouvement de roulement pour simplifier l’analyse. La contrainte de corps rigide suppose que le châssis du robot est rigide, et la contrainte de mouvement de roulement suppose que tous les points du robot tournent autour du centre de rotation instantané avec la même vitesse angulaire. Cela pourrait être un modèle raisonnable pour une structure simple comme le Turtlebot. Afin de simplifier davantage l’analyse, on suppose qu’il n’y a pas de glissement entre les roues et le sol et que le mouvement du robot peut être représenté de manière adéquate sous la forme d’un modèle bidimensionnel dont le mouvement est limité à un seul plan.
9.7.2 Dérivation de l’algorithme de localisation basé sur EKF
La dérivation suit les équations de la section 9.6. Une prédiction d’état pour l’étape de temps [latex](k+1)[/latex] peut être dérivée des informations disponibles jusqu’à l’étape de temps [latex]k[/latex] :
| [latex]\mathbf{X}(k+1) = f(\mathbf{X}(k),\mathbf{u}(k))[/latex] | (9.34) |
Veuillez noter la représentation abrégée utilisée où [latex]X(k+1)[/latex] représente la prédiction de l’état à l’étape de temps[latex](k +1)[/latex] étant donné les informations jusqu’à l’étape de temps [latex](k)[/latex]. [latex]X(k)[/latex] représente la meilleure estimation disponible à l’étape de temps [latex](k)[/latex] et [latex]u(k)[/latex] représente les entrées de commande vers le pilote du robot à l’étape de temps [latex](k)[/latex] :
| [latex]u(k)=\begin{bmatrix} V(k) \\ \omega(k) \end{bmatrix} [/latex]Où [latex]V(k)[/latex] | (9.35) |
est la vitesse d’avancement du robot à l’étape de temps [latex](k)[/latex] et [latex]ω(k)[/latex] est la vitesse de rotation (vitesse angulaire) à l’étape de temps [latex](k)[/latex]. Par conséquent, le modèle de champ de mouvement peut être décrit comme suit ;
| [latex]\left[\begin{array}{c} x(k+1) \\ y(k+1) \\ \varphi(k+1) \end{array}\right]=\left[\begin{array}{l} x(k)+\Delta T V(k) \cos (\varphi(k)) \\ y(k)+\Delta T V(k) \sin (\varphi(k)) \\ \varphi(k)+\Delta T \omega \end{array}\right][/latex] | (9.36) |
Supposons que le robot effectue une observation à l’étape de temps [latex](k+1)[/latex] avec son capteur embarqué sur une caractéristique particulière de l’environnement. Le capteur est monté sur le robot avec un décalage d’unités a dans la ligne médiane, et les résultats d’observation en informations de distance ([latex]r_i[/latex]) et position ([latex]θ_i[/latex]) relatives à la caractéristique observée, comme illustré dans la Figure 9-10.
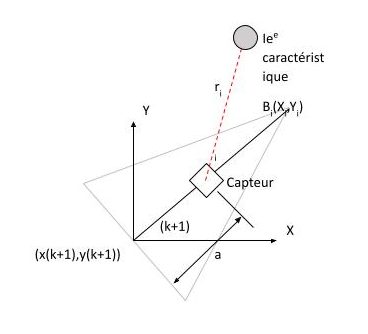
Figure 9-10 : Le capteur monté sur le robot observe la iè caractéristique.
Il existe un nombre n d’entités dispersées dans l’environnement pour lesquelles les coordonnées de position absolue sont connues a priori (c’est-à-dire que les cartes sont données). Une observation générale de l’ie caractéristique [latex]B_{i}(X_{i},Y_{i})[/latex] peut être représentée comme suit :
| [latex]r_i(k+1)= \sqrt{(X_i - x_r(k+1))^2 + (Y_i - y_r(k+1))^2}[/latex] | (9.37) |
| [latex]\theta{_i}(k+1)= \tan ^{-1} \left( \dfrac{( Y_{i}-y_{r}\left( k+1\right) }{( x_{i}-x_{r}\left( k+1\right) }\right) -\varphi(k+1)[/latex] | (9.38) |
où :
| [latex]x_r = x(k) +a~ \cos(\phi(k))[/latex] | (9.39) |
| [latex]y_r = y(k) + a~ \sin(\phi(k))[/latex] | (9.40) |
La meilleure estimation pour cette observation [latex]\mathbf{Z}(k + 1|k)[/latex] dérivée de l’information précédente peut être représentée sous la forme suivante :
| [latex]\mathbf{Z}(k+1)=\left[\begin{array}{l} \hat{Z}_{r}(k+1 \mid k) \\ \hat{Z}_{\theta}(k+1 \mid k) \end{array}\right]=\left[\begin{array}{l} \sqrt{\left(X_{i}-\hat{x}(k+1 \mid k)\right)^{2}+\left(Y_{i}-\hat{y}(k+1 \mid k)\right)^{2}} \\ \tan ^{-1}\left(\frac{\left(Y_{i}-\hat{y}(k+1 \mid k)\right.}{\left(X_{i}-\hat{x}(k+1 \mid k)\right.}\right) \end{array}\right][/latex] | (9.41) |
La prédiction de la covariance peut être obtenue comme
| [latex]P(k+1 \mid k)=\nabla f_{x}(k) P(k \mid k) \nabla f_{x}^{T}(k)+\nabla f_{w}(k) \Sigma(k) \nabla f_{w}^{T}(k)[/latex] | (9.42) |
Où [latex]\nabla f_{x}[/latex] représente le gradient du jacobéen de f (.) évalué à l’instant [latex]k[/latex] par rapport aux états, [latex]\nabla f_{\omega}[/latex] est le jacobéen de f (.) par rapport aux sources de bruit, et [latex]\Sigma(k)[/latex]représente la force du bruit donnée par ;
| [latex]\begin{gathered} \Sigma(k)=\left[\begin{array}{ll} \sigma_{V}^{2} & 0 \\ 0 & \sigma_{\omega}^{2} \end{array}\right] \\ \nabla f_{x}(k)=\left[\begin{array}{lll} 1 & 0 & \Delta T V(k) \sin (\phi(k \mid k)) \\ 0 & 1 & \Delta T V(k) \cos (\phi(k \mid k)) \\ 0 & 0 & 1 \end{array}\right] \\ \nabla f_{w}(k)=\left[\begin{array}{cc} \Delta T \cos (\varphi(k \mid k)) & 0 \\ \Delta T \sin (\varphi(k \mid k)) & 0 \\ 0 & \Delta T \end{array}\right] \end{gathered}[/latex] | (9.43) |
La covariance d’innovation (erreur de prédiction d’observation) [latex]S(k)[/latex], qui est utilisée dans le calcul des gains de Kalman, peut être calculée en mettant au carré l’erreur d’observation estimée et en prenant les attentes des mesures jusqu’à la ke étape de temps et peut s’écrire comme suit ;
| [latex]S(k+1)=\nabla h_{x}(k+1) P(k+1 \mid k) \nabla h_{x}^{T}(k+1)+R(k+1)[/latex] | (9.44) |
Où [latex]R(k + 1)[/latex] est la variance d’observation (qui est diagonale dans la plupart des applications robotiques en raison de la nature indépendante des mesures)
| [latex]\begin{gathered} R(k)=\left[\begin{array}{cc} \sigma_{r}^{2} & 0 \\ 0 & \sigma_{\theta}^{2} \end{array}\right] \\ \nabla h_{x}(k+1)=\left[\begin{array}{ccc} \frac{\hat{x}(k+1 \mid k)-X_{i}}{d} & \frac{\hat{y}(k+1 \mid k)-Y_{i}}{d} & 0 \\ \frac{-\hat{y}(k+1 \mid k)-Y_{i}}{d^{2}} & \frac{\hat{x}(k+1 \mid k)-X_{i}}{d^{2}} & -1 \end{array}\right] \end{gathered}[/latex] | (9.45) |
où,
| [latex]d = \sqrt{(X_i- \hat{x}_r(k+1))^2 + (Y_i - \hat{y}_r(k+1))^2}[/latex] | (9.46) |
Finalement, les équations de mise à jour d’état pour l’EKF sont données par (adaptation des équations générales dans la section précédente)
| [latex]\hat{x}(k+1 / k+1) = \hat{x}(k+1 |k) + W(k+1) [z(k+1) - h(\hat{x}(k+1|k))][/latex] | (9.47) |
où,
| [latex]W(k+1)= P(k+1|k)\nabla h_{x}^{T} (k+1) S(k+1)^{-1}[/latex] | (9.48) |
Est le gain de Kalman.
L’algorithme est maintenant terminé, et au fur et à mesure que le robot progresse à partir du moment [latex]t=0[/latex] observant l’environnement, il peut être appliqué de manière récursive pour déterminer l’emplacement actuel. Un ensemble de caractéristiques cartographiques doit d’abord être initialisé. Dans l’exemple de la Figure 9-11, nous avons utilisé un ensemble de balises rétroréfléchissantes réparties dans l’environnement. Les emplacements de ces balises ont été prospectés et enregistrés pour l’initialisation. Un télémètre laser SICK a été utilisé pour détecter et mesurer la distance et la position de ces balises.
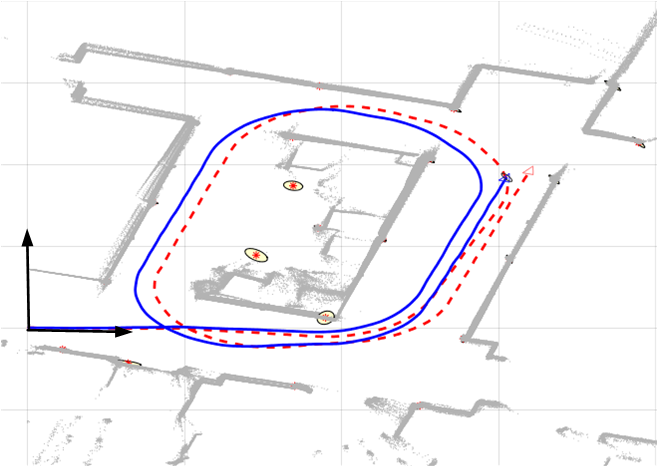
Figure 9-11 : Une implémentation de l’algorithme de localisation basé sur EKF. La ligne bleue continue indique l’estimation EKF de la trajectoire du robot. La ligne pointillée rouge représente l’odométrie. Le * indique les emplacements des balises prospectées.
9.8 Résumé du chapitre
Ce chapitre a examiné brièvement un ensemble de problèmes fondamentaux de la navigation robotique. Le problème de localisation répond à la question « où suis-je? » et le problème de cartographie pose la question « comment générer une carte de l’environnement du robot? » lorsque la position du robot est connue. Le problème de localisation et de cartographie simultanés (SLAM) consiste à résoudre simultanément le problème de localisation et le problème de cartographie. Nous avons discuté d’une approche théorique d’estimation pour résoudre ces problèmes en utilisant des techniques probabilistes. Le filtre de Kalman étendu (EKF) a été présenté comme une mise en œuvre de cette approche utilisant une approximation linéaire des modèles de systèmes non linéaires. En combinant ces algorithmes et techniques, votre robot devrait permettre à votre robot de ne jamais se perdre dans l’espace (ou sur terre!).
9.9 Questions de révision
- Imaginons un robot équipé d’un capteur capable de détecter l’état d’une porte, qui peut être soit ouverte soit fermée. Pour simplifier, supposons que la porte puisse être dans un seul des deux états possibles, ouverte ou fermée. Supposons maintenant que les capteurs du robot soient affectés par du bruit. Le bruit est caractérisé par les probabilités conditionnelles suivantes : (Z-observation, X-état de la porte)
p(Z=sense_open | X = is_open) = 0,63
p(Z=sense_closed | X = is_closed) = 0,95
Quelle est la valeur de la probabilité conditionnelle p(Z=sens_fermé | X = is_open)
- Qu’entend-on par problème de localisation du robot?
- Pourquoi l’association de données est-elle importante pour une localisation réussie?
9.10 Lectures supplémentaires
Ce chapitre n’a fait qu’effleurer la surface du problème de localisation et de cartographie. Des recherches considérables ont eu lieu depuis les années 90, avec de nombreuses implémentations réussies maintenant dans diverses plates-formes de production fonctionnant dans des environnements à grande échelle. Un excellent livre sur le sujet par (Thrun, Burgard, & Fox, 2005) fournit une excellente plongée en profondeur dans le sujet. Le tutoriel essentiel sur SLAM par Bailey et Durrant-Whyte (Bailey & Durrant-Whyte, 2006; Durrant-Whyte & Bailey, 2006) fournit une excellente référence rapide au problème SLAM. Le travail séminal de (Dissanayake, Newman, Clark, Durrant-Whyte, & Csorba, 2001) apporte la preuve de l’existence d’une solution au problème SLAM. Si vous souhaitez comprendre les techniques et théories d’estimation probabilistes sous-jacentes, (Bar-Shalom, Li et Kirubarajan, 2001), est fortement recommandé.
Elfes, A. (1989). Using occupancy grids for mobile robot perception and navigation. Computer, 22(6), 46 – 57. https://doi.org/10.1109/2.30720
Grisetti, G., Stachniss, C., & Burgard, W. (2007). Improved Techniques for Grid Mapping With Rao-Blackwellized Particle Filters. Robotics, IEEE Transactions on, 23(1), 34-46. Retrieved from 10.1109/TRO.2006.889486 http://dx.doi.org/10.1109/TRO.2006.889486
RÉFÉRENCES
Bailey, T., & Durrant-Whyte, H. (2006). Simultaneous localization and mapping (SLAM): part II. Robotics & Automation Magazine, IEEE, 13(3), 108-117. Retrieved from 10.1109/MRA.2006.1678144 http://dx.doi.org/10.1109/MRA.2006.1678144
Bar-Shalom, Y., Li, X.-R., & Kirubarajan, T. (2001). Estimation with Applications to Tracking and Navigation. Somerset, New Jersey: Wiley InterScience. https://doi.org/10.1002/0471221279
Dissanayake, M. W. M. G., Newman, P., Clark, S., Durrant-Whyte, H. F., & Csorba, M. (2001). A Solution to the Simultaneous Localization and Map Building (SLAM) Problem. IEEE TRANSACTIONS ON ROBOTICS AND AUTOMATION, 17(3), 229-241. https://doi.org/10.1109/70.938381
Durrant-Whyte, H., & Bailey, T. (2006). Simultaneous Localisation and Mapping (SLAM): Part I The Essential Algorithms. https://doi.org/10.1109/MRA.2006.1638022
Thrun, S., Burgard, W., & Fox, D. (2005). Probabilistic Robotics Cambridge, Mass.: MIT Press. https://docs.ufpr.br/~danielsantos/ProbabilisticRobotics.pdf
Attributions
Figure 9-5
Taprobana de Ptolémée est dans le domaine public (CC0).
Liste des figures
Figure 9-2 : Un robot se déplaçant dans un référentiel de coordonnées local.
Figure 9-4 : Localisation basée sur la carte.
Figure 9-9 : Un exemple de localisation de robot 1-D
Figure 9-10 : Le capteur monté sur le robot observe la iè caractéristique.

