Analyse de circuits logiques séquentiels synchrones

Guy Bégin

8 Analyse de circuits logiques séquentiels synchrones

1.1. Objectifs

Analyser en détail le comportement d’un circuit séquentiel synchrone à partir de son schéma, selon différents types de bascules employés
Établir les équations de transition qui commandent les bascules
Se familiariser avec la notion de tableau d’excitation
Tracer un diagramme d’état
Interpréter le comportement du système à partir de son diagramme d’état
Faire la distinction entre les deux modèles de circuits séquentiels (Mealy et Moore)

1.2. Démarche d’analyse

Analyser un circuit logique séquentiel a pour but de déterminer le comportement qu’aura le circuit selon les séquences d’entrée qui lui seront appliquées et l’état dans lequel il se trouve initialement. On voudra aussi connaître quelles séquences de sortie seront produites.

Dans la mesure où un circuit comporte une ou des bascules (peu importe le type) et un signal d’horloge, on peut considérer qu’il s’agit d’un circuit séquentiel synchrone. Le type de bascule sera pris en compte pour l’analyse, qui consistera à déterminer, pour un état présent donné, quels seront les prochains états possibles selon les valeurs d’entrée.

Les grandes lignes de la démarche sont les suivantes.

Identification des éléments fonctionnels :
1. entrées externes
2. éléments de mémoire
3. décodeur de prochain état
4. sorties externes
5. décodeur de sortie
Expressions logiques du décodeur de prochain état : établies pour chaque entrée des bascules, en fonction des entrées externes et des variables d’état
Expressions logiques des sorties externes, établies en fonction des entrées externes et des variables d’état
Construction du tableau d’excitation
Diagramme d’état
Interprétation du comportement du circuit séquentiel

Au centre de ce processus se trouve l’analyse des circuits combinatoires qui déterminent ce que seront les entrées des bascules. Nous chercherons à établir les équations de transition qui précisent ce que sera le prochain état en fonction des entrées et de l’état présent.

1.3. Exemple d’analyse

Nous allons appliquer la démarche à un exemple qui nous permettra de mieux expliquer chacune des étapes. Considérons le circuit de la figure 1.

Circuit séquentiel synchrone à analyser.

Figure 1 : Circuit séquentiel synchrone à analyser

Identification des éléments fonctionnels :
1. Il y a une seule entrée externe $I$
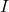
2. Il y a deux éléments de mémoire, étiquetés 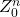$Z_0^n$ et $Z_1^n$
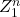
3. On a un décodeur de prochain état pour deux bascules D
4. Il y a deux sorties externes : 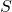$S$ et $U$
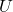
5. Il y a un décodeur de sortie
Expressions logiques pour le décodeur de prochain état :
$Z_0^{n+1} = I \cdot (Z_1^n)^\prime + I \cdot Z_0^n$

$Z_1^{n+1} = I \cdot Z_1^n + Z_0^n$
Expressions logiques des sorties externes :
$S = Z_0^n \cdot (Z_1^{n})^\prime$

$U = Z_0^n \cdot Z_1^{n}$
Tableau d’excitation: chaque ligne du tableau d’excitation (tableau 1) montre, à gauche, un état présent (identifiable par les valeurs de bascules) et une combinaison de valeurs d’entrée, et à droite, le prochain état et les valeurs de sortie produites.

Tableau 1 : Tableau d’excitation pour l’exemple
$Z_1^n$	$Z_0^n$	$I$	$Z_1^{n+1}$	$Z_0^{n+1}$	$S$	$U$
0	0	0	0	0	0	0
0	0	1	0	1	0	0
0	1	0	1	0	1	0
0	1	1	1	1	1	0
1	0	0	0	0	0	0
1	0	1	1	0	0	0
1	1	0	1	0	0	1
1	1	1	1	1	0	1

Diagramme d’état: le diagramme d’état représente de façon schématique le comportement du circuit séquentiel. Les cercles correspondent aux différents états dans lesquels le système peut se trouver. On peut utiliser des étiquettes à l’intérieur des cercles pour nommer les états. On peut aussi y indiquer les numéros d’état (soit en vecteurs de bits, soit avec des nombres binaires comme ici sur la figure). Les sorties produites par le système sont aussi indiquées dans les cercles. Les transitions entre les états sont indiquées par des flèches. Une flèche qui revient vers le même cercle signifie que l’état ne change pas.Les conditions appliquées aux entrées pour déclencher les transitions sont indiquées sur les flèches. Dans la figure, on voit aussi l’état initial, identifié par une flèche partant d’un gros point noir.Le diagramme d’état se construit aisément à partir du tableau d’excitation.

Figure 2 : Diagramme d’état
Interprétation du comportement du circuit séquentiel: le système est initialement à l’état a. Tant que l’entrée 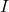$I$ est 0, il demeure dans cet état. Lorsque 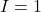$I=1$ , on passe à l’état b. Si 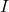$I$ reste à 1, on passe à l’état d et on boucle sur l’état d. Si 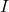$I$ revient à 0, de l’état b ou d, on passe à l’état c. De l’état c, si 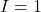$I = 1$ , on reste dans l’état c. Sinon ( 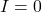$I = 0$ ), on retourne à l’état a. La figure 3 montre une trace des formes d’onde observées en fonctionnement pour le système. Dans cet exemple, le système boucle d’abord sur l’état a (valeur 0 sur la trace), puis passe à l’état b (valeur 1) et ensuite à l’état d (valeur 3), boucle sur l’état d et passe ensuite à l’état c (valeur 2) pour finalement revenir à l’état a.

Figure 3 : Exemple de fonctionnement

1.4. Analyse pour des bascules JK

Pour analyser un circuit séquentiel utilisant des bascules JK, on détermine d’abord les expressions $J_A$ et $K_A$ , $J_B$ et $K_B$ , etc., pour chacune des bascules. On doit ensuite se référer au tableau caractéristique pour ce type de bascule (tableau caractéristique JK) pour déterminer quelles seront les prochaines valeurs de sortie pour chacune des bascules. L’exemple suivant illustre la procédure.

1.4.1. Exemple avec bascules JK

Considérons le circuit séquentiel de la figure 4.

Exemple de circuit séquentiel avec des bascules JK.

Figure 4 : Exemple de circuit séquentiel avec des bascules JK

À partir des expressions des entrées $J$ et $K$ suivantes :

$J_0 = (q_1^{n})^\prime$

$K_0 = q_0^{n} \cdot (q_1^{n})^\prime$

$J_1 = q_0^{n}$

$K_1 = (q_0^{n})^\prime \cdot q_1^{n}$

on peut remplir le tableau d’excitation (tableau 2).

Tableau 2 : Tableau d’excitation circuit séquentiel JK
$q_1^{n+1}$	$q_0^n$	$J_0$	$K_0$	$J_1$	$K_1$	$q_1^{n+1}$	$q_0^{n+1}$
0	0	1	0	0	0	0	1
0	1	1	1	1	0	1	0
1	0	0	0	0	1	0	0
1	1	0	0	1	0	1	1

À partir du tableau d’excitation, on peut tracer le diagramme d’état (figure 5).

Diagramme d'état du circuit séquentiel avec bascules JK.

Figure 5 : Diagramme d’état du circuit séquentiel avec bascules JK

1.5. Modèles de machines séquentielles

On appelle les modèles abstraits de systèmes séquentiels des automates finis ou des machines à état fini (en anglais, Finite State Machines (FSM)). On distingue deux modèles de circuits séquentiels, selon la façon dont les sorties sont obtenues. Dans le modèle de Mealy, les sorties dépendent à la fois des entrées et des variables d’état présent (figure 6). Dans le modèle de Moore, les sorties ne dépendent que des variables d’état présent (figure 7).

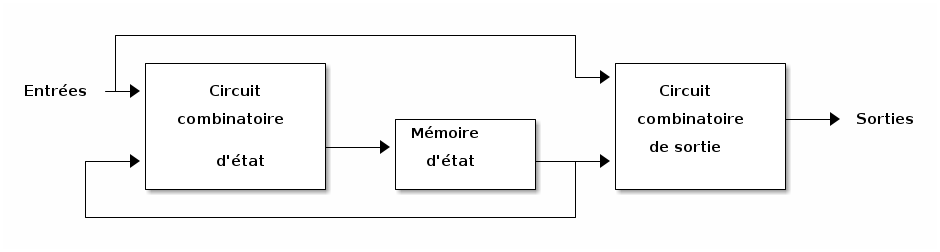
Machine de Mealy.

Figure 6 : Machine de Mealy

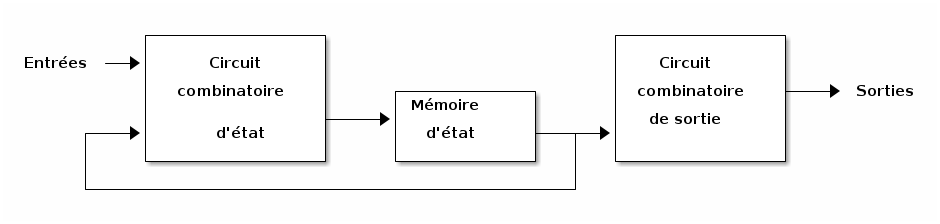
Machine de Moore.

Figure 7 : Machine de Moore

Quiz de fin de chapitre

Considérez circuit séquentiel décrit par le diagramme d’état suivant:

Diagramme d'état

En utilisant l’assignation d’états a = 00, b = 01, c = 10, d = 11, et les sorties dans l’ordre, Z et F, construisez le tableau d’état pour ce circuit séquentiel en faisant glisser les valeurs d’états et de sortie aux bons endroits du tableau d’état.

Complétez l’automate fini pour le circuit séquentiel, en faisant glisser les valeurs d’entrées et de sorties sur les transitions.

Licence

Symbole de License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International

Circuits logiques combinatoires et séquentiels Copyright © 2023 by Guy Bégin is licensed under a License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, except where otherwise noted.