Circuits séquentiels

Guy Bégin

7 Circuits séquentiels

1.1. Objectifs

Identifier un circuit logique séquentiel
Faire la distinction entre les circuits séquentiels synchrones et asynchrones
Se familiariser avec les principaux types de loquets, en expliquer le fonctionnement
Se familiariser avec les principaux types de bascules, en expliquer le fonctionnement

1.2. Modèle d’un circuit séquentiel

Les circuits logiques séquentiels sont ceux qui comportent de la mémoire. Le modèle général d’un circuit séquentiel est illustré sur la figure 1. On y voit qu’il y a une boucle de rétroaction, qui fait que les valeurs binaires stockées dans les éléments de mémoire contribuent au calcul des sorties. Les sorties du circuit à un instant donné ne dépendent donc pas seulement des entrées présentes à ce moment, mais aussi de ces valeurs qui sont mémorisées dans le système. Pour décrire cette situation dans laquelle se trouvent les valeurs stockées en mémoire, on parle de l’état du système. Selon les entrées et l’état à un instant donné, le système pourra changer d’état selon les changements qui seront apportés par la portion combinatoire aux valeurs mémorisées.

On verra donc le système évoluer au fil du temps, passant d’un état à un autre, et générant des sorties en fonction des entrées et de l’état du moment. Intuitivement, on peut penser que le nombre d’états distincts sera fonction du nombre de valeurs binaires qui seront mémorisées. Le comportement d’un système séquentiel est donc caractérisé par une séquence temporelle d’entrées, de sorties et de valeurs internes d’état.

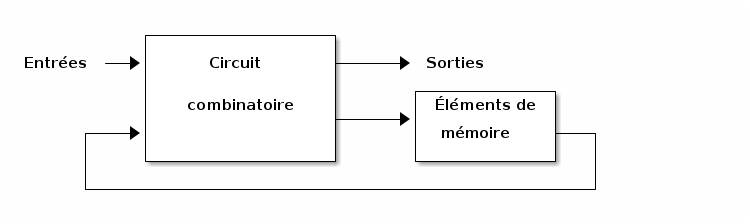
Modèle de circuit séquentiel.

Figure 1 : Modèle de circuit séquentiel

On peut distinguer les circuits séquentiels selon la relation de synchronisation qui existe entre les différents signaux du système. Dans un circuit séquentiel synchrone, le comportement du système peut se définir en fonction des valeurs de ses signaux à des instants discrets prédéterminés.

Le comportement d’un circuit séquentiel asynchrone dépend à tout moment des signaux d’entrée et de l’ordre dans lequel ces signaux changent.

Un circuit séquentiel synchrone fait appel à un signal spécial appelé horloge qui rythme les changements d’état et de sorties afin qu’ils se produisent à des instants discrets. Les éléments de mémoire qui stockent les valeurs binaires sont appelés bascules (flip-flops en anglais). Il existe différents types de bascules. Nous les étudierons en détail, car elles sont à la base des circuits séquentiels les plus utilisés. La figure 2 présente le modèle général d’un circuit séquentiel synchrone.

Modèle de circuit séquentiel synchrone.

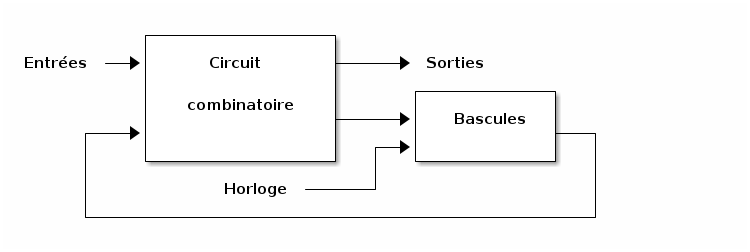
Figure 2 : Modèle de circuit séquentiel synchrone

Le signal d’horloge est typiquement une onde carrée, comme illustré sur la figure 3.

Signal d'horloge en onde carrée.

Figure 3 : Signal d’horloge

1.3. Éléments de mémoire

Un élément de mémoire peut maintenir son état binaire indéfiniment (à condition, évidemment, qu’il soit alimenté). Son état est observable par l’intermédiaire de ses sorties. On doit agir via la ou les entrées de l’élément pour le faire changer d’état. Les différents types d’éléments de mémoire sont caractérisés par le nombre et le type d’entrées.

Les éléments de mémoire qui sont contrôlés par les niveaux de leurs entrées sont appelés des loquets (latches en anglais). Les éléments contrôlés par des changements ou transitions de niveaux sont appelés des bascules. Les transitions sont appliquées à une entrée spéciale d’horloge qui sert à déclencher les changements d’état à des instants précis. Les loquets sont des ingrédients de base dans la conception des bascules. Nous les étudierons en premier.

1.4. Loquets

1.4.1. Loquet SR

Le loquet SR est formé de deux portes NOR interconnectées et comporte deux entrées : $S$ pour Set, qui permet de mémoriser une valeur 1, et $R$ pour Reset, qui permet de mémoriser une valeur 0. Le schéma classique du loquet SR montré sur la figure 4 ne fait pas ressortir la boucle de rétroaction, mais si on déplace un peu les éléments sans changer les connexions, on voit mieux le lien de retour caractéristique de la boucle. Sur la figure 5, la porte reliée à $S$ a été placée devant, mais nous aurions pu tout aussi bien mettre l’autre porte en avant. Aucune des deux n’est vraiment devant l’autre, puisqu’il s’agit d’une boucle n’ayant ni début ni fin.

Schéma du loquet SR avec portes NOR.

Figure 4 : Schéma du loquet SR avec portes NOR

Schéma du loquet SR NOR mettant la boucle en évidence.

Figure 5 : Schéma du loquet SR NOR mettant la boucle en évidence

Quand les sorties sont $Q=1, Q^\prime=0$ , on dit que le loquet est dans l’état activé (set). Lorsque $Q=0, Q^\prime=1$ , le loquet est désactivé (reset). Les sorties $Q$ et $Q^\prime$ sont normalement complémentaires. Si on active la condition d’entrée $S=1, R=1$ , les deux sorties seront à 0, mais lorsqu’on relâchera les entrées, le loquet passera à un état imprévisible, voire instable. Dans une application normale, on voudra éviter le cas d’entrée $S=1, R=1$ .

En fonctionnement normal, à moins de vouloir changer l’état, on garde les deux entrées à $S=0, R=0$ et l’état du loquet se maintient. En appliquant le niveau 1 pendant un certain temps à $S$ seulement, le loquet s’active, peu importe l’état dans lequel il se trouvait auparavant. On doit s’assurer de ramener l’entrée $S$ à 0 avant d’apporter d’autres changements aux entrées, pour éviter le cas interdit $S=1, R=1$ .

De même, en appliquant le niveau 1 pendant un certain temps à $R$ seulement, le loquet se désactive, peu importe l’état dans lequel il se trouvait auparavant.

Tableau 1 : Loquet SR NOR : tableau de fonctionnement
$S$	$R$	$Q$	$Q^\prime$
1	0	1	0
0	0	1	0	après $s=1, R=0$
0	1	0	1
0	0	0	1	après $s=0, R=1$
1	1	0	0	interdit

On peut aussi concevoir un loquet avec des portes NAND, comme sur la figure 6. Le fonctionnement est sensiblement le même, si ce n’est que les niveaux sont inversés par rapport au loquet NOR comme on peut le voir sur le tableau de fonctionnement (tableau 2). Par exemple, on garde les deux entrées à $S=1, R=1$ pour maintenir l’état du loquet.

Schéma du loquet SR en portes NAND.

Figure 6 : Loquet SR en portes NAND

Tableau 2 : Loquet SR NAND : tableau de fonctionnement
$S$	$R$	$Q$	$Q^\prime$
1	0	0	1
1	1	0	1	après $s=1, R=0$
0	1	1	0
1	1	1	0	après $s=0, R=1$
0	0	1	1	interdit

On peut ajouter un signal de contrôle d’entrée $E$ (enable) pour contrôler quand le loquet pourra être affecté par les signaux d’entrée. Le circuit est représenté à la figure 7. Comme on peut voir dans le tableau 3, les sorties des portes NAND d’entrée demeurent à 1 tant que $E = 0$ , et le loquet ne peut pas être affecté par les entrées $S$ et $R$ . Quand on active $E = 1$ , le circuit peut être actionné par les entrées $S$ et $R$ . La condition pour activer est $S=1, R=0$ ; pour désactiver, c’est $S=0, R=1$ . Lorsque $E = 1$ , on ne doit pas faire $S=1, R=1$ , car on mettrait le loquet dans un état indéterminé.

Le loquet SR avec contrôle est surtout important comme ingrédient de base pour la conception de bascules.

Loquet SR NAND avec signal de contrôle.

Figure 7 : Loquet SR NAND avec signal de contrôle

Tableau 3 : Loquet SR avec signal de contrôle : tableau de fonctionnement
$E$	$S$	$R$	Prochain $Q$
0	X	X	inchangé
1	0	0	inchangé
1	0	1	$Q = 0$
1	1	0	$Q = 1$
1	1	1	indéterminé

1.4.2. Loquet D

Une option pour éliminer la condition qui fait apparaître un état indéterminé est de s’assurer de toujours commander $S$ et $R$ avec des signaux complémentaires. C’est ainsi qu’on arrive au loquet D, illustré sur la figure 8, qui ne comporte qu’une entrée de donnée $D$ et une entrée de contrôle $E$ . La valeur de $D$ est reflétée à $Q$ lorsque $E=1$ et se maintient après que $E$ passe à 0 (tableau 4).

Schéma du loquet D.

Figure 8 : Schéma du loquet D

Tableau 4 : Loquet D : tableau de fonctionnement
$E$	$D$	Prochain $Q$
0	X	inchangé
1	0	$Q = 0$
1	1	$Q = 1$

Le symbole graphique d’un loquet D est illustré à la figure 9.

Symbole du loquet D.

Figure 9 : Symbole du loquet D

1.5. Application : rebonds d’interrupteurs

Lorsqu’on utilise un interrupteur pour commuter un signal entre les niveaux qui correspondent aux valeurs logiques 0 et 1, le contact ne se fait pas de façon franche sans hésitations, et le signal observé rebondit plusieurs fois avant de se stabiliser à sa valeur, comme on peut le voir sur la partie de gauche de la figure 10. Ces rapides allers-retours entre les niveaux peuvent bien souvent déclencher un circuit logique et le mettre dans un état imprévisible. Pour éviter ce problème, on peut faire appel à un loquet selon la configuration de la partie droite de la figure. Le loquet réagit dès que l’entrée B passe à 0. Même si cette entrée remonte à 1, la valeur $Q$ est maintenue. On obtient donc une transition franche sur $Q$ .

[À gauche, exemple de signal observé quand l'interrupteur simple commute; à droite, schéma d'un circuit à loquet permettant d'enclencher une transition des le premier contact et signaux observés.

Figure 10 : Contacts et rebonds

1.6. Bascules (Flip-flops)

Les loquets peuvent remplir le rôle de mémoriser des valeurs binaires, mais le fait que les changements d’état soient activés par un niveau pose des difficultés. En effet, si les valeurs à l’entrée changent pendant que le signal de contrôle est actif, la valeur qui sera mémorisée par la rétroaction sera la dernière qui aura eu le temps de s’y établir, qui ne sera pas nécessairement la valeur souhaitée. Si la sortie du loquet est acheminée, directement ou à travers un circuit combinatoire, vers ses entrées ou les entrées d’autres loquets (activés par le même signal de contrôle) dans une boucle du circuit séquentiel, il se peut que les délais de propagation et de prise en compte des entrées fassent que la sortie globale du circuit séquentiel soit imprévisible.

La conception des bascules vise à corriger ce problème, en établissant un instant précis et prévisible de déclenchement où les valeurs d’entrée seront prises en compte systématiquement. Le concept essentiel est que l’état d’une bascule est modifié uniquement au moment où il y a un changement dans son signal de contrôle. Ce changement momentané est appelé transition et on dit que c’est la transition qui provoque le changement d’état qui déclenche la bascule.

On parlera de déclenchement sur le front montant lorsque la transition qui provoque le déclenchement passe d’un niveau bas vers un niveau élevé, et de déclenchement sur le front descendant dans le cas d’une transition du haut vers le bas. On illustre parfois le front de déclenchement au moyen d’une flèche, comme on peut le voir sur la figure 11.

Signaux d'horloge avec fronts de déclenchement.

Figure 11 : Signaux d’horloge avec fronts de déclenchement

1.6.1. Bascule D

Le secret pour isoler la valeur mémorisée par l’élément de mémoire des changements qui pourraient survenir sur les entrées consiste à utiliser un mécanisme semblable à celui d’un sas. Selon le /Larousse/, la définition d’un sas est

Enceinte ou passage clos, muni de deux portes ou systèmes de fermeture dont on ne peut ouvrir l’un que si l’autre est fermé et qui permet de passer ou de faire passer d’un milieu à un autre en maintenant ceux-ci isolés l’un de l’autre.

Dans notre contexte, nous utiliserons deux loquets en série, avec la sortie du premier, appelé maître, reliée à l’entrée du deuxième, appelé esclave. Le loquet maître sera activé par le signal d’horloge, alors que le loquet esclave sera activé par le complément du signal d’horloge. De cette façon, un seul des loquets sera actif à la fois, comme dans un sas. La figure 12 illustre la configuration pour réaliser une bascule D maître-esclave.

Schéma d'une bascule D maître-esclave.

Figure 12 : Bascule D maître-esclave

Lorsque le signal d’horloge est au niveau haut, seul le loquet maître pourra réagir au signal d’entrée. Puis, lorsque le signal d’horloge sera au niveau bas, ce premier loquet sera désactivé, sa sortie sera maintenue, et le deuxième loquet sera activé. Comme l’entrée du loquet esclave est alimentée par le loquet maître dont la sortie est maintenue, c’est la valeur mémorisée par le maître qui sera mémorisée dans l’esclave et qui apparaîtra donc en sortie de l’ensemble.

La valeur qui sera ultimement mémorisée est celle qui se trouvait tout juste avant la transition de l’horloge passant du niveau haut vers le niveau bas. Nous avons donc créé une bascule sensible au front descendant.

En résumé :

La sortie 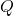$Q$ ne changera qu’une fois par cycle d’horloge.
Un changement de valeur sera causé par la valeur d’entrée présente juste avant le front descendant de l’horloge.
La valeur de sortie changera effectivement (s’il y a lieu) pendant la demi-période basse de l’horloge.

D’autres configurations permettent de réaliser ce comportement de sas. Par exemple, le circuit de la figure 13 utilise trois éléments en loquet SR NAND : les deux premiers sont activés par le signal de donnée $D$ et l’horloge, et le dernier mémorise et fournit le signal de sortie $Q$ . Cette configuration réalise une bascule D à déclenchement sur front montant.

Schéma d'une bascule D à déclenchement sur front montant.

Figure 13 : Bascule D à déclenchement sur front montant

Pour bien comprendre le comportement du circuit, la série de figures suivantes permet d’en suivre le fonctionnement. Sur les figures, les valeurs binaires sont indiquées par des couleurs : un signal en vert sombre dénote la valeur 0 et un signal en vert clair représente la valeur 1.

Comme on peut le voir sur la figure 14, lorsque $clk = 0$ , les entrées intermédiaires $S$ et $R$ sont maintenues au niveau 1, quelle que soit la valeur de l’entrée $D$ , ce qui assure de maintenir la valeur de sortie en $Q$ .

Bascule au repos clk = 0, D=0.

Figure 14 : Bascule au repos $clk = 0, D=0$

Même lorsque l’entrée de donnée $D$ change, la valeur de sortie est maintenue, comme on le voit sur la figure 15.

Bascule au repos clk = 0, D passe à 1.

Figure 15 : Bascule au repos $clk = 0, D \rightarrow 1$

Si l’entrée de donnée $D = 0$ lorsque $clk$ passe à 1, $R$ devient 0, ce qui met $Q$ à 0 (opération reset) (figure 16).

Bascule opération reset, clk passe à 1, D=0.

Figure 16 : Bascule reset $clk \rightarrow 1, D=0$

Si l’entrée de donnée $D$ change pendant que $clk = 1$ , comme sur la figure 17, $R$ reste à 0, parce que la porte NAND à trois entrées a ses trois entrées à 1 : par le signal $clk = 1$ , par la rétroaction du signal $S$ et par le signal de sortie de la porte NAND du bas.

Bascule, clk = 1, D passe à 1.

Figure 17 : Bascule $clk = 1, D \rightarrow 1$

Quand $clk$ revient à 0, on a $S= 1, R=1$ et la sortie $Q$ ne peut plus changer.

La figure 18 présente la bascule dans l’état $Q=0$ avec l’entrée de donnée $D = 1$ , juste avant que $clk$ passe à 1. On voit que les deux portes NAND du haut sont prêtes à provoquer un changement d’état de $S$ lorsque l’horloge passera à 1.

Bascule clk = 0, D = 1.

Figure 18 : Bascule $clk =0, D = 1$

Si l’entrée de donnée $D = 1$ lorsque $clk$ passe à 1, on voit que $S$ est devenu 1, ce qui a amené $Q$ à 1 (opération set) (figure 19).

Bascule opération set clk passe à 1, D=1.

Figure 19 : Bascule set $clk \rightarrow 1, D=1$

La figure 20 présente un chronogramme qui montre la bascule qui passe de l’état 0 à l’état 1 et retourne, au cycle suivant, à l’état 0.

Chronogramme pour une bascule D.

Figure 20 : Chronogramme pour une bascule D

1.6.2. Délais et réponse temporelle

Comme dans tout circuit logique, les changements de valeurs logiques dans les différentes portes qui constituent une bascule ne sont pas instantanés. Il faut donc laisser le temps nécessaire pour que les changements puissent se propager, être pris en compte et se stabiliser.

Sur la figure 21, on indique le délai $t_{setup}$ entre le moment où la valeur à l’entrée de donnée D est modifiée et la prochaine transition de déclenchement de l’horloge. Pour assurer un fonctionnement adéquat de la bascule, on doit respecter un temps de mise en place (setup) minimum pendant lequel la valeur à l’entrée de donnée D doit être maintenue avant la transition de déclenchement.

On montre aussi sur la figure le délai $t_{hold}$ entre le moment de déclenchement et un prochain changement de valeur à l’entrée de donnée D. Pour un fonctionnement adéquat, on doit également respecter un temps de maintien (hold) minimum pendant lequel la valeur à l’entrée de donnée D doit être maintenue après la transition de déclenchement de l’horloge.

Enfin, la figure montre le délai de propagation à la sortie de la bascule $t_{prop}$ , qui se mesure entre le moment du déclenchement et le moment où la sortie se stabilise à sa nouvelle valeur.

Chronogramme avec temps et délais.

Figure 21 : Chronogramme avec temps et délais

Le symbole graphique d’une bascule D comporte un petit triangle à l’entrée d’horloge pour indiquer que le déclenchement se fait sur une transition. Un déclenchement sur front descendant est indiqué par un petit cercle d’inversion à l’entrée d’horloge.

Symboles de bascules.

Figure 22 : Symboles de bascules

1.6.3. Autres bascules

Il y a essentiellement trois opérations possibles pour une bascule : mettre sa sortie à 1 (set), mettre sa sortie à 0 (reset) ou faire basculer son état de sortie (toggle).

1.6.4. Bascule JK

Une bascule JK comporte deux entrées, ce qui permet de lui faire exécuter les trois opérations. Activer seulement l’entrée $J$ fait un set, activer seulement l’entrée $K$ fait un reset et activer les deux entrées fait un toggle. On peut réaliser une bascule JK comme sur la figure 23.

Schéma d'une bascule JK.

Figure 23 : Bascule JK

La figure 24 montre le chronogramme de fonctionnement d’une bascule JK. La bascule fait d’abord un set, puis un reset et enfin trois toggles de suite.

Chronogramme de la bascule JK.

Figure 24 : Chronogramme de la bascule JK

1.6.5. Bascule T

La bascule T (T pour toggle) change d’état à chaque déclenchement lorsque l’entrée $T$ est activée. On peut la réaliser à partir d’une bascule D ou d’une bascule JK (figure 25).

Schéma d'une bascule T: en haut, à partir d'une bascule JK; en bas, à partir d'une bascule D.

Figure 25 : Bascule T

1.6.6. Tableaux caractéristiques

On résume le fonctionnement des différentes bascules au moyen de tableaux qui décrivent, selon les conditions d’entrée et l’état présent, quel sera le prochain état après le déclenchement. $Q(t)$ représente l’état présent et $Q(t+1)$ l’état suivant.

Tableau 5 : Bascule D
$D$	$Q(t+1)$
0	0		reset
1	1		set

Tableau 6 : Bascule JK
$J$	$K$	$Q(t+1)$
0	0	$Q(t)$	pas de changement
0	1	0	reset
1	0	1	set
1	1	$Q^\prime(t)$	basculement

Tableau 7 : Bascule T
$T$		$Q(t+1)$
0		$Q(t)$	pas de changement
1		$Q^\prime(t)$	basculement

1.6.7. Équations caractéristiques

On peut de même formuler des équations qui décrivent le comportement des bascules. Pour une bascule D, on a

$Q(t+1) = D$

Pour une bascule JK, on a

$Q(t+1) =J Q^\prime + K^\prime Q$

Pour une bascule T, on a

$Q(t+1) = T \operatorname{Xor} Q = T Q^\prime + T^\prime Q$

1.6.8. Entrées asynchrones

Certaines bascules sont aussi munies d’entrées asynchrones, dont l’effet n’est pas soumis à l’horloge. Ces entrées sont typiquement utilisées pour faire un reset ou un set de la bascule, par exemple pour une remise à zéro initiale d’un circuit séquentiel. Une configuration typique est illustrée par la bascule de la figure 26 qui comporte une entrée Reset', laquelle permet de forcer l’état en agissant sur une porte NAND de chacune des paires de portes. Cette entrée est active au niveau bas, c’est pourquoi il y a une indication de complément dans son symbole.

Bascule D avec reset asynchrone.

Figure 26 : Bascule D avec reset asynchrone

Quiz de fin de chapitre

Déplacez les indications de temps/délais sur le chronogramme suivant.

Licence

Symbole de License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International

Circuits logiques combinatoires et séquentiels Droit d'auteur © 2023 par Guy Bégin est sous licence License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, sauf indication contraire.