Conception de circuits logiques séquentiels

Guy Bégin

9 Conception de circuits logiques séquentiels

1.1. Objectifs

Concevoir un circuit logique séquentiel synchrone à partir d’une spécification fonctionnelle
Construire un diagramme d’état en fonction d’un besoin
Construire un tableau d’état en fonction d’un diagramme d’état
Réduire le nombre d’états nécessaires
Assigner des codes binaires aux états et choisir une approche
Concevoir un décodeur de prochain état et un décodeur de sortie

1.2. Conception d’un circuit séquentiel synchrone

Concevoir un circuit logique séquentiel permet de répondre à un besoin pratique qui ne peut pas être satisfait par un circuit combinatoire. Le point de départ est une description, la plus précise possible, du besoin à satisfaire : quelle doivent être la ou les entrées, les sorties ou conditions qui font passer d’un état au suivant, etc. Pour un besoin donné, une multitude de solutions fonctionnellement équivalentes sont possibles; ainsi il faudra établir des critères ou identifier des contraintes qui permettront d’orienter la conception et le choix final d’une solution. Deux systèmes peuvent avoir un même comportement vu de l’extérieur, mais comporter des nombres d’états internes différents.

Des considérations pratiques nous amèneront souvent à vouloir réduire le nombre d’états nécessaires, et à simplifier les différents circuits combinatoires utilisés. Réduire le nombre de bascules utilisées ne se traduit pas toujours par un système plus simple, car les décodeurs d’état et de sortie peuvent alors s’en trouver plus complexes.

1.3. Spécification fonctionnelle

Comme dans tout problème de conception, la formulation en mots de la spécification du système est cruciale. Appliquer parfaitement une procédure de conception en se basant sur une spécification erronée ne peut pas conduire à un système adéquat.

Il faudra un bon bagage d’expérience et d’intuition au concepteur ou à la conceptrice pour pouvoir interpréter et traduire correctement une description informelle, très souvent incomplète, ambiguë et imprécise, et la traduire correctement en un design concret qui répond à un besoin maladroitement exprimé. Il revient à cette personne de s’assurer que ce quelle a compris correspond bien à ce qui était demandé.

La première question à poser est : Que doit faire le système? Suivront d’autres questions, amenant à définir davantage de détails : Doit-il y avoir des entrées? Si oui, combien? Combien de sorties sont nécessaires? Le comportement du système pourra être essentiellement caractérisé en répondant à la question : Quelle doit être la séquence des sorties, pour une certaine séquence d’entrées? Mais comme les séquences d’entrées peuvent être en nombre infini, il faudra identifier des patrons qui permettront de résumer le comportement du système.

1.4. Diagramme d’état

Un diagramme d’état préliminaire est un bon point de départ pour définir et étudier le comportement du système. On identifiera les différents états par des lettres pour les distinguer sans faire référence à des variables binaires associées à des éléments de mémoire. Il s’agit dans un premier temps d’un diagramme préliminaire, parce que le diagramme final qui sera implémenté sera potentiellement différent.

À partir du diagramme d’état, il est possible de vérifier quelle séquence de sortie correspond à une séquence d’entrée donnée, et ainsi de valider le comportement.

1.5. Tableau d’état

Un tableau d’état comporte une ligne par état présent et combinaison d’entrées. Selon les combinaisons d’entrées possibles, on donne le prochain état et les valeurs de sortie.

1.6. Réduction du nombre d’états

Deux états sont équivalents si, pour chaque combinaison d’entrées, ils produisent la même sortie et amènent le système dans le même état ou dans un état équivalent. Considérons le diagramme d’état de la figure 1 et le tableau d’état correspondant (tableau 2). On peut voir qu’il s’agit ici d’une machine de Mealy, car les valeurs de sortie sont associées aux transitions.

Diagramme d'état avant réduction.

Figure 1 : Diagramme d’état avant réduction

Tableau 1 : Tableau d’état initial
État présent	$x$	État suivant	$S$
a	0	b	1
a	1	f	1
b	0	d	0
b	1	c	1
c	0	d	0
c	1	e	0
d	0	b	1
d	1	c	1
e	0	e	1
e	1	a	1
f	0	d	0
f	1	e	0

En inspectant les différents états, on voit que les états c et f sont équivalents. En remplaçant l’état f par l’état c, on obtient le nouveau tableau d’état (tableau 2).

Tableau 2 : Tableau d’état après une simplification
État présent	$x$	État suivant	$S$
a	0	b	1
a	1	c	1
b	0	d	0
b	1	c	1
c	0	d	0
c	1	e	0
d	0	b	1
d	1	c	1
e	0	e	1
e	1	a	1

On voit maintenant que les états a et d sont équivalents. En remplaçant l’état d par l’état a, on obtient le tableau d’état simplifié (tableau 3). Il n’y a plus de simplification possible. Nous sommes passés de six états à quatre.

Tableau 3 : Tableau d’état simplifié
État présent	$x$	État suivant	$S$
a	0	b	1
a	1	c	1
b	0	d	0
b	1	c	1
c	0	d	0
c	1	e	0
e	0	e	1
e	1	a	1

Il faut bien s’assurer que le tableau d’état simplifié produit les séquences de sortie désirées selon les séquences d’entrée appliquées.

1.6.1. Tableau d’implication

La méthode du tableau d’implication facilite l’identification des états redondants à éliminer. Considérons le tableau d’état suivant, qui correspond cette fois-ci à une machine de Moore dont nous allons réduire le nombre d’états.

Tableau 4 : Tableau d’état (machine de Moore)
État présent	État suivant	État suivant	$S$
	$x=0$	$x=1$
a	g	c	0
b	f	h	0
c	e	d	1
d	a	c	0
e	c	a	1
f	f	b	1
g	a	c	0
h	c	g	1

Un tableau d’implication comporte une entrée pour chaque paire d’états dans le tableau d’état. Avec $n$ états initialement (ici on a $n=8$ ), on étiquettera les colonnes avec les $n-1$ premiers états, et les lignes avec les $n-1$ derniers états. La première case vide, en haut à gauche, sera notée [a;b] et la dernière en bas à droite sera [g;h]. Voici le tableau avant d’être rempli (tableau 5). Seules les cases qui ne comportent pas de _ peuvent être remplies. Il n’y a par exemple rien d’utile à mettre dans une case étiquetée [b;b], et on mettra l’information qui irait dans la case [c;b] dans la case [b;c].

Tableau 5 : Tableau d’implication
b		_	_	_	_	_	_
c			_	_	_	_	_
d				_	_	_	_
e					_	_	_
f						_	_
g							_
h
	a	b	c	d	e	f	g

On applique la procédure en considérant chaque case du tableau, ce qui permet de comparer chaque paire de lignes du tableau d’état.
- On vérifie dans un premier temps si les sorties sont différentes. Si c’est le cas, on met un ✔ dans la case. Par exemple ici, a et c, a et e, a et f, a et h ont des sorties différentes, donc on place des ✔ dans les cases [a;c], [a;e], [a;f] et [a;h].
- Si les sorties sont les mêmes, on place dans la case les paires d’états qu’une équivalence nécessiterait. Par exemple, pour la case [a;b], une équivalence entre a et b nécessiterait les équivalences g=f et c=h entre les états prochains. Pour la case [a;d], une équivalence entre a et d nécessiterait les équivalences g=a et c=c. Cette dernière, évidente, n’est pas inscrite dans le tableau. Pour [b;d], on trouve f=a et h=c.
- Si les sorties sont les mêmes et les paires d’états suivants sont identiques ou encore sont les états mêmes qu’on est en train de considérer, on met directement OUI dans le tableau. Par exemple pour la case [a;g], on a les paires g=a et c=c, donc on met OUI. Pour la case [d;g], on a a=a et c=c, on met OUI également. On continue ainsi, de colonne en colonne, pour obtenir après ces étapes le résultat suivant (tableau 6).

Tableau 6 : Tableau d’implication, après étape 1
b	g=f c=h	_	_	_	_	_	_
c	✔	✔	_	_	_	_	_
d	g=a	f=a h=c	✔	_	_	_	_
e	✔	✔	d=a	✔	_	_	_
f	✔	✔	e=f d=b	✔	c=f a=b	_	_
g	OUI	f=a h=c	✔	OUI	✔	✔	_
h	✔	✔	e=c d=g	✔	a=g	f=c b=g	✔
	a	b	c	d	e	f	g

L’étape suivante consiste à considérer chaque case qui comporte une ou des paires d’états impliqués. On regarde la case correspondant à chaque paire, et s’il y a un ✔ dans la case, alors l’implication ne fonctionne pas. Par exemple, la case [a;b] repose sur les équivalences g=f et c=h. Or si on regarde la case [f;g], on voit qu’il s’y trouve un ✔, ce qui veut dire que f et g ne peuvent pas être équivalents, ce qui implique que a et b ne pourront pas être équivalents. Ce n’est pas la peine de regarder la case [c;h]. On remplacera donc les paires de la case [a;b] par un ✔✔, pour faire ressortir ces nouveaux échecs.
Un ✔✔ dans le tableau peut faire échouer d’autres implications. Il faut donc revoir les cases avec des paires d’états impliqués pour voir s’il faut changer leur statut. On continue à revoir ainsi jusqu’à ce qu’il n’y ait plus d’ajouts de ✔✔. On obtient finalement le tableau suivant (tableau 7).

Tableau 7 : Tableau d’implication, après étape 3
b	✔✔	_	_	_	_	_	_
c	✔	✔	_	_	_	_	_
d	g=a	✔✔	✔	_	_	_	_
e	✔	✔	d=a	✔	_	_	_
f	✔	✔	✔✔	✔	✔✔	_	_
g	OUI	✔✔	✔	OUI	✔	✔	_
h	✔	✔	e=c d=g	✔	a=g	✔✔	✔
	a	b	c	d	e	f	g

Après cette étape, toutes les cases qui contiennent OUI ou des paires d’implications indiquent des équivalences d’états. Ici, on a les équivalences suivantes : a=d, a=g, c=e, c=h, d=g, e=h. Les états uniques résultants sont a, b, c et f. On obtient le tableau d’état réduit suivant (tableau 8).

Tableau 8 : Tableau d’état réduit (machine de Moore)
État présent	État suivant	État suivant	$S$
	$x=0$	$x=1$
a	a	c	0
b	f	c	0
c	c	a	1
f	f	b	1

1.7. Codage des états

Une fois que le nombre d’états a été réduit, il faut assigner des codes binaires aux états. Si on doit coder $m$ états, il faudra $n$ bits, avec $2^n \geq m$ . Si le nombre de combinaisons binaires est plus grand que le nombre d’états nécessaires, les combinaisons inutilisées seront considérées comme des cas facultatifs.

Le choix d’une assignation des codes aux états aura des répercussions sur la complexité du décodeur de prochain état et sur le décodeur de sortie. Plusieurs options peuvent être envisagées : assigner des codes dans l’ordre naturel d’énumération binaire, assigner selon un code Gray, ou encore choisir une assignation où il y a un seul bit 1 par code binaire (approche dite one-hot). L’approche one-hot requiert plus de bascules, mais permet souvent de simplifier les décodeurs de prochain état et de sortie. Le tableau 9 montre un exemple possible d’assignation pour chacune de ces approches.

Tableau 9 : Possibilités d’assignation de codes d’états
État	Binaire	Gray	One-hot
a	00	00	0001
b	01	01	0010
c	10	11	0100
e	11	10	1000

1.8. Décodeur d’état

Après avoir décidé d’une assignation, on refait le tableau d’état simplifié en remplaçant les étiquettes d’états symboliques par les codes binaires correspondants. On obtient ainsi un tableau de transition, qui permet d’élaborer les expressions logiques pour le décodeur de prochain état. Le type de bascules à utiliser déterminera les sorties nécessaires pour le décodeur d’état, en se basant sur les tableaux caractéristiques de la section Tableaux caractéristiques.

1.9. Décodeur de sortie

Une fois que le codage d’état est établi, la conception du décodeur de sortie est directe. Un tableau de vérité avec comme entrées les valeurs binaires d’états et comme sorties les valeurs de sorties externes permet de déterminer les fonctions combinatoires à implémenter.

1.10. Procédure de conception

La conception d’un circuit séquentiel suit une procédure bien définie. Étant donnée la complexité de cette tâche, on limite la conception manuelle à des circuits relativement petits. Pour des besoins plus ambitieux, des outils de synthèse automatisés ont été développés. Ces procédures automatisées supposent typiquement des bascules D, car la correspondance entre l’entrée et la prochaine sortie est directe. Voici les étapes à suivre :

À partir de la description et des spécifications du comportement souhaité, concevoir un diagramme d’état
Réduire le nombre d’état (si pertinent)
Assigner des codes binaires aux états
Remplir le tableau de transition
Sélectionner un type de bascules à utiliser
Déterminer les expressions simplifiées pour le décodeur de prochain état et le décodeur de sortie
Tracer le schéma logique du circuit

1.11. Exemple de conception

On doit concevoir un circuit séquentiel qui détecte la séquence binaire 101 lorsqu’elle apparaît dans sa séquence d’entrée. Une fois la séquence identifiée, le système produira une sortie 1 et demeurera dans le même état en continuant de produire une sortie 1, jusqu’à une remise à zéro.

1.11.1. Bascules D

1. Diagramme d’état
  
  Selon le diagramme d’état de la figure 2, le système démarre dans l’état a et demeure dans cet état tant que l’entrée 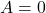$A=0$ . Lorsque 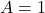$A=1$ , on passe à l’état b, début de la reconnaissance du patron 101. Ensuite, si 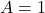$A=1$ , on reste dans l’état b parce que ce pourrait être le début d’une autre séquence 101. De l’état b, si 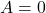$A=0$ , on passe à l’état c, car on a observé 10 en séquence. De l’état c, si on a 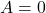$A=0$ , la séquence observée est maintenant de 100 et on doit tout recommencer en retournant à l’état a. De l’état c, si on a 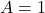$A=1$ , alors on a reconnu la séquence 101. On met la sortie 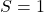$S=1$ et on reste dans cet état pour toutes les autres transitions, quelle que soit l’entrée. Il s’agit ici d’une machine de Moore, puisque la sortie 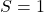$S=1$ est produite lorsqu’on est dans l’état d; on a 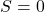$S=0$ dans les autres états.
  
  Figure 2 : Diagramme d’état pour détecter la séquence 101
Réduction d’états

Il n’y a pas de réduction d’états possible ici.
Assigner des codes binaires aux états

Pour quatre états, il nous faudra deux bascules. Le tableau 10 présente l’assignation d’états choisie.

Tableau 10 : Tableau d’assignation d’état

État Code

a 00

b 01

c 10

d 11
Remplir le tableau de transition

Le tableau 11 donne les transitions d’états.

Tableau 11 : Tableau de transition d’états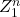

$Z_1^n$ $Z_0^n$ $A$ $Z_1^{n+1}$ $Z_0^{n+1}$ $S$

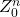
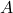
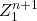
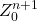
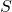
0 0 0 0 0 0

0 0 1 0 1 0

0 1 0 1 0 0

0 1 1 0 1 0

1 0 0 0 0 0

1 0 1 1 1 0

1 1 0 1 1 1

1 1 1 1 1 1
Sélectionner un type de bascules à utiliser

On choisit des bascules D.
Déterminer les expressions simplifiées

Les diagrammes de Karnaugh correspondants sont donnés pour 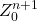$Z_0^{n+1}$ (figure 3), 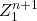$Z_1^{n+1}$ (figure 4) et 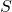$S$ (figure 5).

Notons que la convention d’étiquetage des diagrammes est différente de ce que nous avons vu précédemment. Au lieu d’étiqueter les lignes et les colonnes avec bits de minterms, on indique ici à l’extérieur du diagramme proprement dit les variables (telles quelles ou complémentées) et les régions du diagramme où on les retrouve. Par exemple, en dessous du diagramme de la figure 3, on indique à partir de la gauche, une première région où la variable 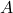$A$ est complémentée (première colonne à gauche), puis une région correspondant à deux colonnes où la variable est telle quelle (deux colonnes du centre), et enfin une région où la variable est complémentée (colonne du centre).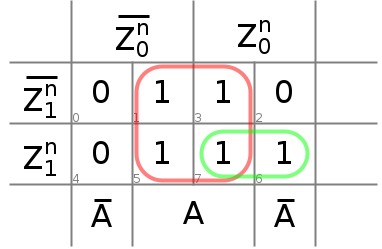

$Diag-K pour Z_0^{n+1}.$

Figure 3  : Diag-K pour $Z_0^{n+1}$

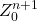
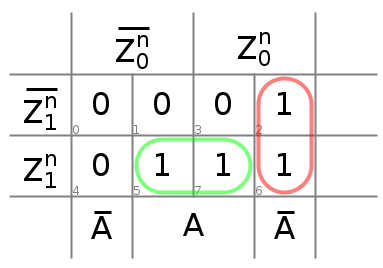
$diag-Diag-K pour Z_1^{n+1}.$

Figure 4  : Diag-K pour $Z_1^{n+1}$

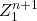
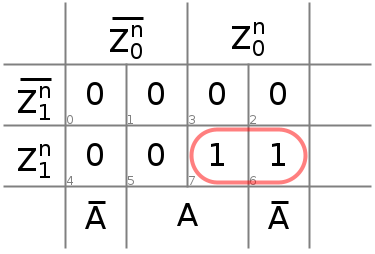
Figure 5  : Diag-K pour $S$
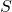
Décodeur de prochain état

Les expressions pour le décodeur de prochain état sont :

$Z_1^{n+1} = (A^\prime \cdot Z_0^{n}) + (A \cdot Z_1^{n})$

$Z_0^{n+1} = A + (Z_0^{n} \cdot Z_1^{n})$
Décodeur de sortie

L’expression pour le décodeur de sortie est :

$S = Z_0^{n} \cdot Z_1^{n}$
Tracer le schéma logique du circuit

Le circuit obtenu est représenté sur la figure 6. On montre sur la figure 7 une trace d’exécution. Les premiers coups d’horloge, l’entrée 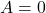$A=0$ et le système demeure dans l’état 0. Puis, lorsque 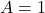$A=1$ , on passe à l’état 1. Comme 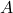$A$ reste à 1, on demeure dans l’état 1 un certain temps. Puis, lorsque 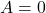$A=0$ , on passe à l’état 2. Avec 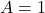$A=1$ de nouveau, on passe à l’état 3 en activant la sortie 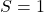$S=1$ . On ne quittera plus cet état par la suite. Une deuxième trace d’exécution (figure 8 ) montre un cas où le système retourne à l’état 0 après avoir reçu une séquence 100.

Figure 6  : Détecteur pour la séquence 101

Figure 7  : Trace d’exécution avec succès

Figure 8  : Trace d’exécution sans succès

1.11.2. Autres types de bascules

Les fonctions du décodeur de prochain état se formulent naturellement en fonction de bascules D. Pour faire l’implémentation avec des bascules JK ou T, il faut pouvoir déterminer les entrées nécessaires pour amener les changements d’état requis. Pour ce faire, on utilisera des tableaux d’excitation qui listent les combinaisons d’entrées pour passer d’un état présent $Q_n$ à un état prochain $Q_{n+1}$ . Le tableau d’excitation pour une bascule JK est donné dans le tableau 12 et celui pour une bascule T est donné dans le tableau 13.

Tableau 12 : Tableau d’excitation, bascule JK
$Q_n$	$Q_{n+1}$	$J$	$K$
0	0	0	X
0	1	1	X
1	0	X	1
1	1	X	0

Tableau 13 : Tableau d’excitation, bascule T
$Q_n$	$Q_{n+1}$	$T$
0	0	0
0	1	1
1	0	1
1	1	0

Reprenons le tableau de transition d’états pour notre exemple, tableau 11, en ajoutant les signaux à générer pour des bascules JK. On obtient alors le tableau 14.

Tableau 14 : Tableau de transition d’états, avec bascules JK
$Z_1^n$	$Z_0^n$	$A$	$Z_1^{n+1}$	$J$	$K$	$Z_0^{n+1}$	$J$	$K$
0	0	0	0	0	X	0	0	X
0	0	1	0	0	X	1	1	X
0	1	0	1	1	X	0	X	1
0	1	1	0	0	X	1	X	0
1	0	0	0	X	1	0	0	X
1	0	1	1	X	0	1	1	X
1	1	0	1	X	0	1	x	0
1	1	1	1	X	0	1	x	0

On trouve les expressions simplifiées suivantes :

$J_{Z_1} = A^\prime \cdot Z_0^n$

$K_{Z_1} = A^\prime \cdot (Z_0^n)^\prime$

$J_{Z_0} = A$

$K_{Z_0} = (A + Z_1^n)^\prime$

Ce qui nous donne l’implémentation de la figure 9.

Détecteur pour la séquence 101, bascules JK.

Figure 9 : Détecteur pour la séquence 101, bascules JK

1.12. États interdits

Lorsque le nombre d’états nécessaires pour le fonctionnement de l’automate fini est strictement inférieur au nombre total d’états possibles avec les bascules utilisées, un certain nombre d’états (physiques) ne seront pas utilisés dans le fonctionnement normal du circuit séquentiel. On parlera alors d’états interdits. Lors de la formulation des tableaux de vérité pour le décodeur de prochain état, ces états donneront lieu à des cas facultatifs, qui pourront permettre la simplification du circuit combinatoire du décodeur.

Il faut toutefois se méfier de scénarios dans lesquels l’automate fini pourrait se retrouver dans un tel état interdit en raison d’un dysfonctionnement momentané ou lors de la mise en marche du système. Considérons par exemple un circuit séquentiel dont le diagramme d’état (tel qu’implémenté après conception) est illustré ci-dessous (figure 10). En fonctionnement normal, le système évolue entre les états a, b et c. Mais si pour une raison quelconque, le système entre dans l’état d, il restera coincé en bouclant sur cet état pour toujours (ou peut-être jusqu’à un prochain dysfonctionnement).

Diagramme d'état avec état interdit.

Figure 10 : Diagramme d’état avec état interdit

Une solution serait de modifier le décodeur de prochain état pour s’assurer que, de l’état interdit, on revient toujours vers un état normal, comme on peut le voir sur la figure suivante (figure 11), où de l’état d, on reviendra toujours vers l’état c.

Diagramme d'état qui assure le retour en fonctionnement normal.

Figure 11 : Diagramme d’état qui assure le retour en fonctionnement normal

1.13. Exemple avec états one-hot

Dans l’exemple suivant, on explore l’assignation d’états one-hot dans laquelle il n’y a qu’un bit 1 par code binaire.

Considérons le diagramme d’état suivant (figure 12).

Diagramme d'état pour assignation one-hot.

Figure 12 : Diagramme d’état pour assignation one-hot

Le tableau d’assignation d’état correspondant est donné dans le tableau 15 ci-dessous.

Tableau 15 : Assignation *one-hot*
État	One-hot
a	100
b	010
c	001

Chaque état aura sa propre bascule active, dont les sorties seront dénotées $A$ , $B$ et $C$ . Le tableau de transition d’états qu’on obtient comporte un grand nombre de cas facultatifs et d’états inutilisés, que nous n’avons pas indiqués ici. Le tableau 16 ne montre que les six transitions spécifiées dans le diagramme d’état.

Tableau 16 : Tableau de transition d’états *one-hot*
$A^n$	$B^n$	$C^n$	$x$	$y$	$z$	$A^{n+1}$	$B^{n+1}$	$C^{n+1}$
0	0	1	0	X	X	0	0	1
0	0	1	1	X	X	0	1	0
0	1	0	X	0	0	0	1	0
0	1	0	X	0	1	0	0	1
0	1	0	X	1	X	1	0	0
1	0	0	X	X	X	0	0	1

Il est possible de formuler le décodeur de prochain état directement, par inspection des transitions spécifiées. Si on considère les transitions qui entrent dans l’état a, il y a trois façons différentes d’arriver en a :

à partir de a, sous la condition $x=0$
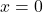
à partir de b, sous la condition $y=0, z=1$
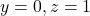
à partir de c, sans conditions

L’équation de prochain état pour a sera ainsi

$A^{n+1} = A^{n}x^\prime + B^n y^\prime z + C^n$

Le même raisonnement nous permet d’écrire pour les autres bascules :

$B^{n+1} = A^{n}x + B^n y^\prime z^\prime$

et

$C^{n+1} = B^n y$

Le décodeur de prochain état est simplifié, car les bits d’état offrent une indication directe de l’état dans lequel la machine se trouve. Le fonctionnement de la machine entraîne peu de transitions, ce qui se traduit en une consommation d’énergie réduite et moins de risque d’aléas glitches. La vitesse de commutation ne dépend pas du nombre d’états. IIl est possible d’ajouter ou de retrancher un état sans avoir à tout refaire la conception. L’assignation one-hot est particulièrement intéressante lorsqu’il y a moins de contraintes sur le nombre de bascules que sur le nombre d’éléments combinatoires.

Le principal inconvénient de cette approche est la croissance du nombre de bascules, qui est linéaire avec le nombre d’états plutôt que logarithmique. Par exemple, pour 30 états, il faudra 30 bascules alors qu’avec un encodage binaire, il n’en faudrait que cinq. Il faut aussi considérer qu’il y a un grand nombre d’états interdits et prendre les précautions qui s’imposent pour éviter les problèmes de fonctionnement coincé.

Quiz de fin de chapitre

Déterminez le diagramme d’état pour un circuit séquentiel synchrone avec une entrée $x$ et une sortie $z$ qui est utilisé pour reconnaître la séquence d’entrée 101. La sortie doit donc être $z=1$ lorsque le dernier 1 de la séquence 101 est identifié. $z$ est ensuite remis à zéro au prochain coup d’horloge. Les chevauchements de 101 ne sont pas permis. Par exemple,

$x = 010101101$

$z = 000100001$

Faites glisser les valeurs d’entrée et de sortie sur les transitions du diagramme.

Licence

Symbole de License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International

Circuits logiques combinatoires et séquentiels Copyright © 2023 by Guy Bégin is licensed under a License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, except where otherwise noted.

$Z_1^n$	$Z_0^n$	$A$	$Z_1^{n+1}$	$J$	$K$	$Z_0^{n+1}$	$J$	$K$
0	0	0	0	0	X	0	0	X
0	0	1	0	0	X	1	1	X
0	1	0	1	1	X	0	X	1
0	1	1	0	0	X	1	X	0
1	0	0	0	X	1	0	0	X
1	0	1	1	X	0	1	1	X
1	1	0	1	X	0	1	x	0
1	1	1	1	X	0	1	x	0

Tableau 10 : Tableau d’assignation d’état
État	Code
a	00
b	01
c	10
d	11

$Z_1^n$	$Z_0^n$	$A$	$Z_1^{n+1}$	$J$	$K$	$Z_0^{n+1}$	$J$	$K$
0	0	0	0	0	X	0	0	X
0	0	1	0	0	X	1	1	X
0	1	0	1	1	X	0	X	1
0	1	1	0	0	X	1	X	0
1	0	0	0	X	1	0	0	X
1	0	1	1	X	0	1	1	X
1	1	0	1	X	0	1	x	0
1	1	1	1	X	0	1	x	0