2 Modélisation par éléments finis de la réponse vibroacoustique de l’oreille externe occluse par un protecteur auditif
Dans cette section, on discute des différentes façons de modéliser le comportement vibratoire/acoustique de l’oreille externe occluse par un protecteur auditif à l’aide de modèles EF élaborés par les auteurs. Les développements sont présentés pour des excitations stationnaires et la résolution du problème est faite dans le domaine fréquentiel. On adopte une description de la mécanique des milieux continus pour l’ensemble du système tête/protecteur. Les mouvements du fluide et des domaines poreux[1] sont décrits par un champ de pression acoustique et celui des domaines solides par un champ de déplacement, respectivement solutions de l’équation de Helmholtz avec ou sans dissipation et des équations de l’élastodynamique.
On aborde la modélisation géométrique de chacune des structures anatomiques pertinentes de la tête et des protecteurs auditifs, les lois de comportement, les conditions aux limites et de chargement, le maillage et les méthodes de résolution. Pour évaluer les modèles proposés, on montre quelques exemples de comparaisons mesures/calculs dans le cas d’une excitation par bruit stationnaire.
Géométrie
Oreille externe – tête sans protecteur
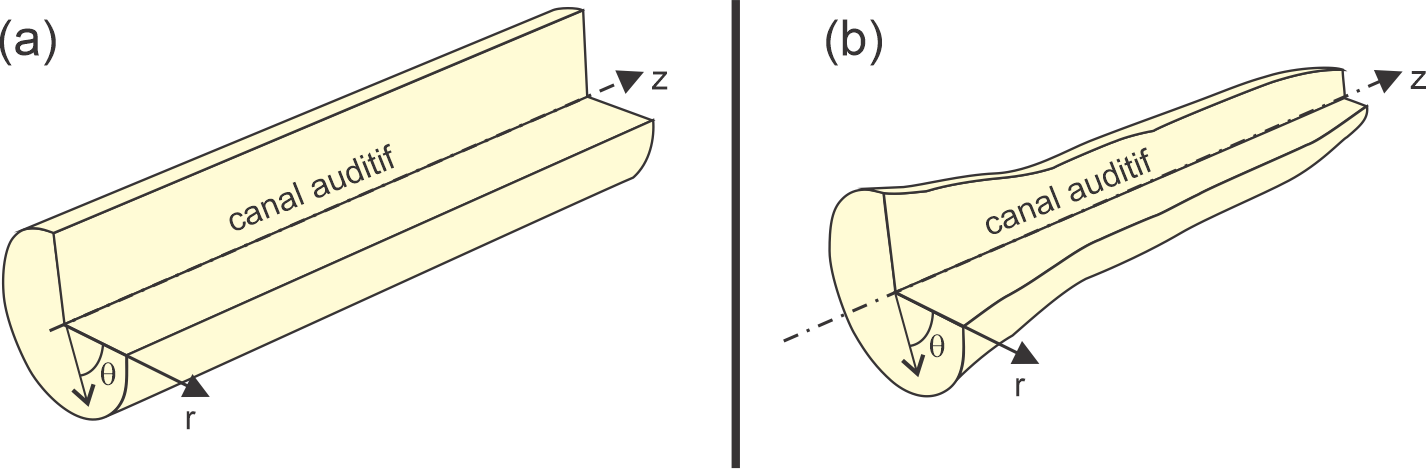
Différents niveaux de simplification de la géométrie de l’oreille externe peuvent être envisagés (Figure 13 à Figure 16). Dans le cas où on ne s’intéresse qu’à la conduction aérienne, un premier niveau de simplification consiste à représenter le canal auditif par un canal cylindrique droit à section constante circulaire rempli d’air aux parois rigides (Figure 13a) de même longueur. Se pose cependant la question du choix de la section droite (volume équivalent, section égale à la section d’entrée du canal 3D ou à celle du tympan). Cette représentation du canal ne permet de pas de reproduire les fonctions de transfert en oreille ouverte sur toute la gamme de fréquences d’intérêt (Viallet et al., 2013). Pour des conditions aux limites et d’excitation symétriques (ex. une onde plane en incidence normale à l’entrée du canal) on peut encore davantage simplifier ce problème 3D en le réduisant à un problème axisymétrique (Viallet et al., 2013). En adoptant un système de coordonnées cylindriques où l’axe [latex]z[/latex] est l’axe de symétrie du canal et [latex]r[/latex] et [latex]\theta[/latex] sont les coordonnées polaires d’un point dans une section droite du cylindre, un modèle axisymétrique élimine la dépendance [latex]\theta[/latex] et le champ de pression acoustique ne dépend plus que de [latex]r[/latex] et [latex]z[/latex]. Il suffit donc de résoudre un problème 2D dans le plan [latex](r ,z)[/latex] et multiplier la solution obtenue par [latex]2\pi[/latex]. Une augmentation en réalisme consiste à considérer un canal cylindrique droit à section circulaire variable (Stinson et Lawton, 1989), toujours à parois rigides, pour prendre en compte le fait que le canal auditif n’a pas une section droite constante mais varie en fonction de la position sur son axe curviligne[2] (Figure 13b). Différentes techniques de construction d’un canal auditif 2D axisymétrique équivalent sont discutées dans (Viallet et al., 2013). En progressant toujours dans le degré de réalisme, la tortuosité du canal auditif et ainsi que la forme exacte de la section droite peuvent être prise en compte. On passe alors à un modèle 3D avec canal aux parois rigides (Viallet et al., 2013) (Figure 14a) avec éventuellement une membrane tympanique flexible (Schmidt et Hudde, 2009). Ce canal peut être également couplé au pavillon de l’oreille (Schmidt et Hudde, 2009; Volandri et al., 2014) et à une tête de forme réaliste (Walsh et al., 2004), eux-mêmes considérés comme rigides acoustiquement ou absorbants (Figure 14b). En fonction de l’enveloppe externe de la structure anatomique à modéliser, des scanners optiques 3D éventuellement intra-auriculaires pour accéder au canal auditif ou encore des empreintes peuvent être utilisés. La technique d’empreinte, très commune pour fabriquer les bouchons moulés ou les aides auditives ou encore évaluer les différences morphologiques intra et inter-sujets, est cependant reconnue pour fournir une forme approchée du canal ouvert puisque la viscosité du silicone utilisé pour le moulage ainsi que les mouvements de la bouche de l’utilisateur lorsqu’il parle ou mâche peuvent modifier la forme réelle du canal. On peut également avoir recours à des techniques plus lourdes comme l’imagerie médicale.
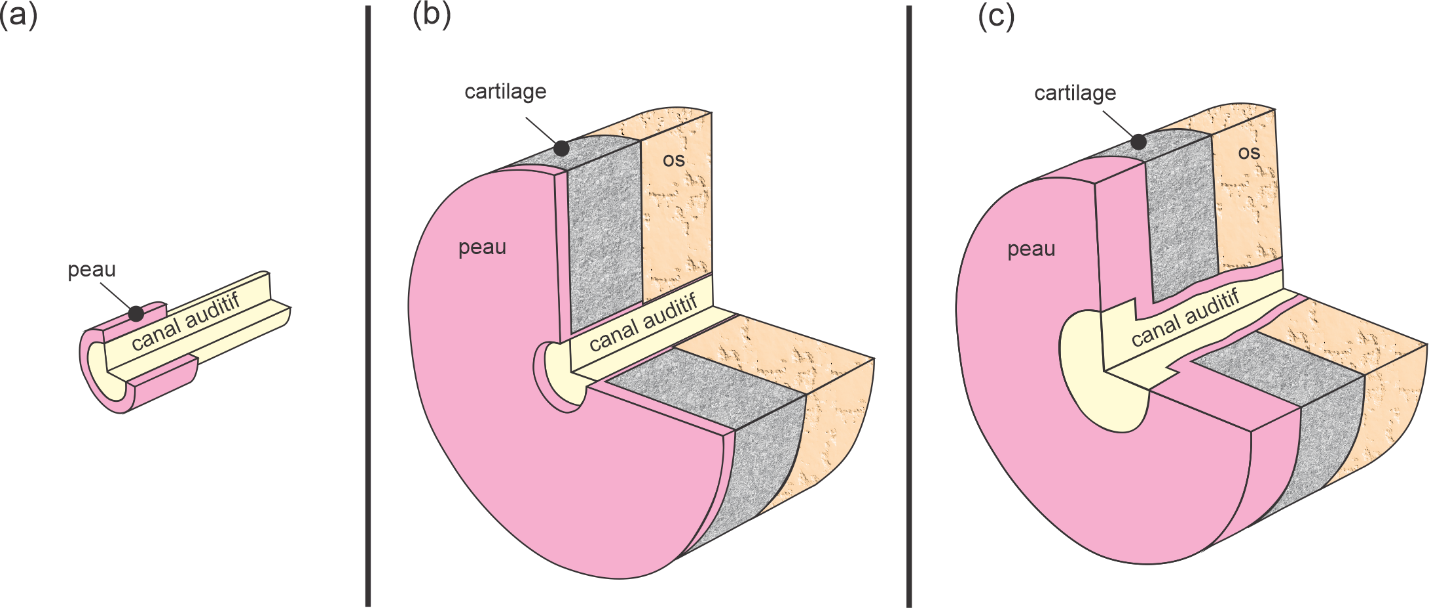
Lorsqu’on s’intéresse à la conduction aérienne mais également celle à travers les tissus environnants (peau, tissus mous (incluant gras, muscle, sang, nerf, tendons, tissus fibreux), cartilage, os) qui peut générer une pression acoustique dans le canal auditif par rayonnement, un modèle de canal cylindrique droit à section circulaire constante rempli d’air mais couplé à une couche élastique reproduisant la peau à l’instar des canaux de têtes artificielles peut être utilisé (Viallet et al., 2014) (Figure 15a). Comme précédemment, ce problème 3D peut être simplifié en un problème axisymétrique pour une excitation et des conditions aux limites symétriques. Cette configuration peut être complexifiée en ajoutant une portion de peau en amont du canal pour représenter le pavillon ainsi qu’une région cartilagineuse et osseuse (Brummund et al., 2015 ; Viallet et al., 2015), en considérant un canal auditif cylindrique droit à section circulaire constante (Figure 15b) ou variable (Figure 15c). Là encore, lorsque l’excitation et les conditions aux limites sont symétriques, on peut ramener le problème 3D à un problème 2D axisymétrique.
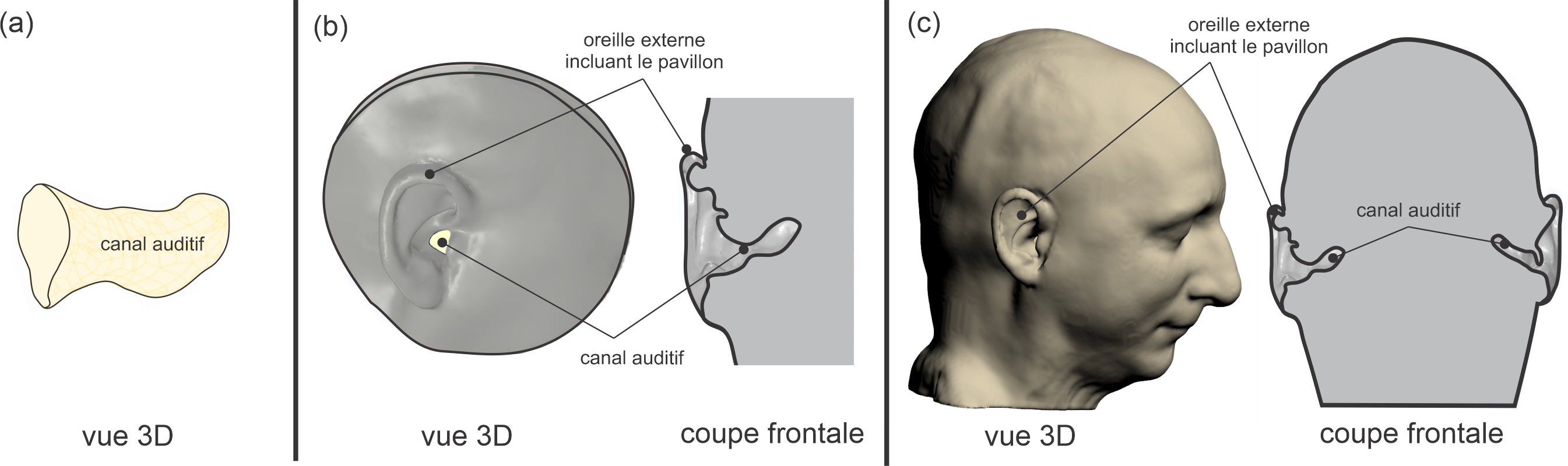
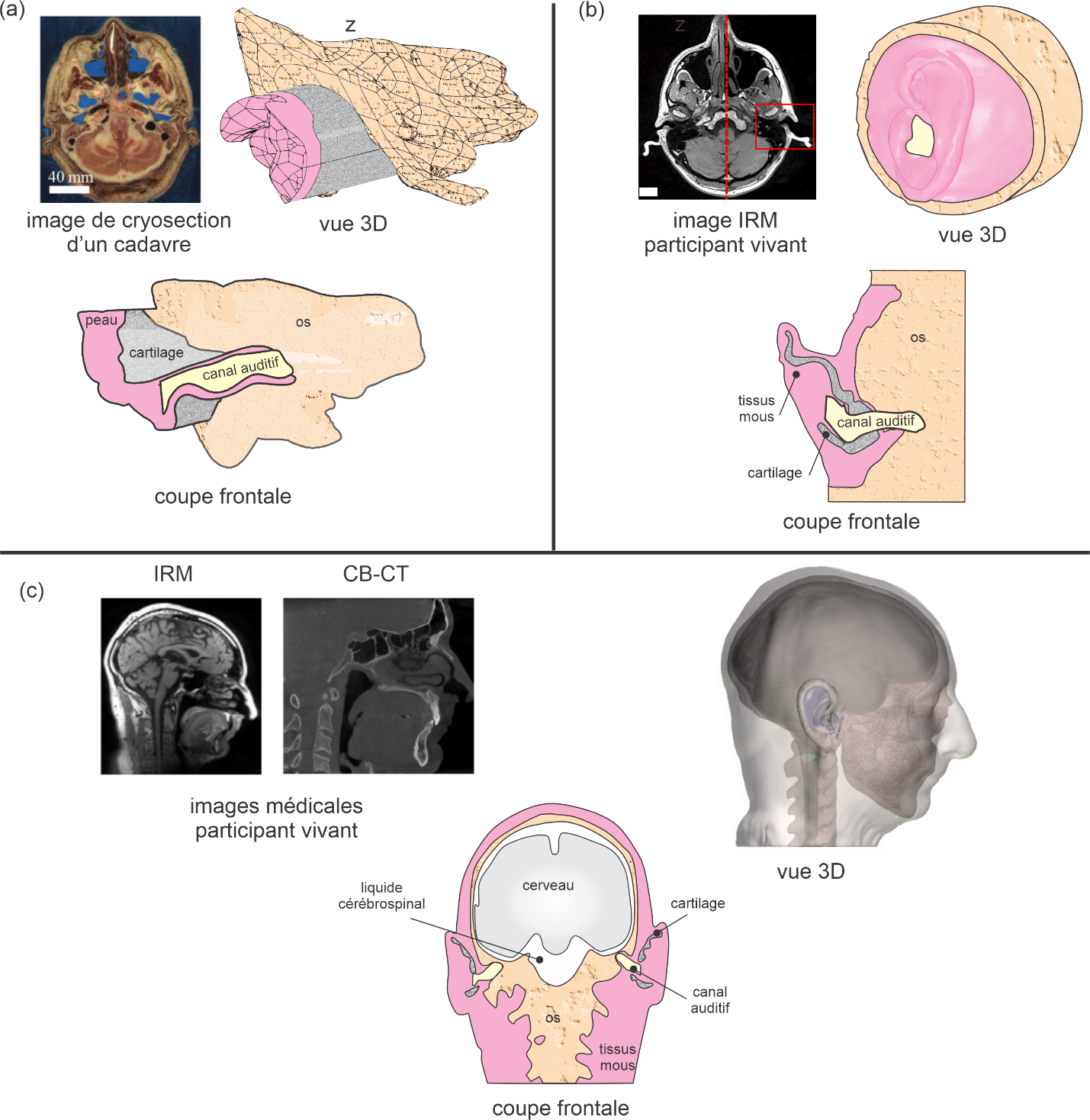
L’étape suivante consiste à prendre en compte le caractère tortueux du canal et la variation de la section droite ainsi qu’une portion des tissus environnants tels que la peau, le cartilage et l’os temporal avec un modèle 3D (Brummund et al., 2014a ; Motallebzadeh et al., 2016, 2017a, 2017b) (Figure 16a sans pavillon et Figure 16b). Dans ces derniers modèles tronqués, l’oreille externe et une partie des tissus environnants sont extraites de la tête. Afin de prendre en compte les phénomènes de conduction osseuse à travers toute la tête, l’étape ultime de réalisme consiste à considérer la tête en entier avec le canal auditif, l’ensemble de la peau, des tissus mous, cartilagineux et osseux mais aussi d’autres structures anatomiques comme le cerveau et le liquide cérébrospinal (Chang et al., 2016 ; Xu et al., 2021), les yeux, l’oreille interne, les différents types d’os (Chang, 2018) (Figure 16c). Notons que certains auteurs intègrent la peau dans les tissus mous mais considèrent le cartilage à part entière (Benacchio et al., 2020a ; Chang et al., 2016 ; Xu, 2021, 2022) alors que d’autres amalgament le cartilage et les tissus mous sous forme de cartilage équivalent, la peau étant considérée en tant que telle (Brummund et al., 2014a). Ces modèles tenant compte de la géométrie réelle des structures anatomiques nécessitent de reconstruire précisément ces structures grâce à des images médicales obtenues par cryosection en coupe d’un cadavre humain du Visible Human Project® ou Visible Korean Project (Brummund et al., 2014a ; Chang et al., 2016; Kim et al., 2014) ou directement sur des sujets humains vivants par résonance magnétique (IRM) ((Benacchio et al., 2019 ; Darkner, 2008 ; Darkner et al., 2007, 2017, 2018 ; Xu, 2021, 2022) ou encore par tomodensitométrie (CT ou CBCT) (Xu, 2021, 2022). L’acquisition d’images par IRM en oreille ouverte pose un défi du fait du bruit intense généré lors des tests. En général, les oreilles du sujet doivent être protégées à l’aide de protecteurs auditifs supra ou intra-auriculaire. Or, l’utilisation de ces protecteurs peut occasionner une déformation du canal auditif par rapport au cas où aucune occlusion n’est utilisée. On peut s’affranchir de ce problème en utilisant des séquences spéciales IRM plus silencieuses qui permettent de respecter les normes d’exposition au bruit pendant la durée du test (Benacchio et al., 2019). La combinaison d’images obtenues par diverses techniques peut s’avérer nécessaire afin de pouvoir distinguer l’ensemble des structures anatomiques. Par exemple, les structures osseuses sont difficiles à reconnaitre sur les images IRM alors qu’avec les images CT Cone-Beam ce n’est pas le cas.
Dans la perspective de l’élaboration d’un modèle permettant de prédire le champ acoustique dans le canal auditif en tenant compte des conductions aérienne et solidienne, se pose la question de la nécessité de modéliser finement la géométrie de l’oreille moyenne et interne. De nombreux travaux ont considéré une telle modélisation (Areias et al., 2016 ; Caminos et al., 2015 ; De Greef et al., 2017 ; Gan et al., 2007 ; Kikidis et al., 2014 ; Lee et al., 2010 ; Lee et Ahn, 2015 ; Ni, 2012 ; Nie et al., 2011 ; Sun et al., 2002 ; Tian et al., 2015 ; Volandri et al., 2012, 2014 ; Wang et al., 2014) mais essentiellement pour comprendre la mécanique de l’oreille moyenne/interne avec un intérêt particulier pour les déplacements de la membrane tympanique ou des osselets, la pression acoustique dans la cavité de l’oreille moyenne ou dans la cochlée ou encore les déplacements de la membrane basilaire plutôt que pour la pression acoustique dans le canal auditif. Ces géométries ont été obtenues à partir d’images de cryosection (projet Visible ear) (Gan et al., 2004, 2007 ; Sun et al., 2002 ; Wang et al., 2007) ou micro CT d’oreilles de cadavres (De Greef et al., 2017 ; Lee et al., 2010 ; Lee et Ahn, 2015 ; Motallebzadeh et al., 2016, 2017a). A notre connaissance, seuls quelques travaux ont considéré des modèles d’oreille moyenne détaillés pour déterminer le champ de pression acoustique dans le canal auditif (Motallebzadeh et al., 2017b ; Schmidt et Hudde, 2009 ; Volandri et al., 2014). La discussion sur la façon de modéliser l’effet acoustique de l’oreille moyenne et interne sur la pression acoustique dans le canal auditif est poursuivie dans la section Couplage entre le fluide du canal auditif et l’oreille moyenne.
Oreille externe – tête avec protecteur
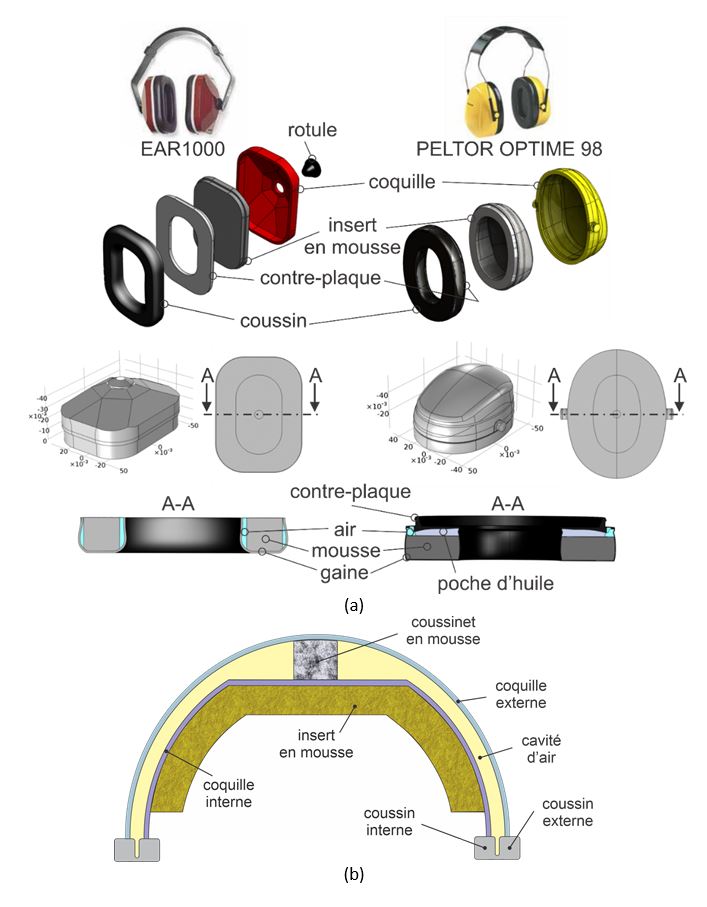
La géométrie nominale (non déformée) du protecteur peut être obtenue à l’aide de mesures au pied à coulisse ou de systèmes optiques. Des exemples de CAD obtenus respectivement pour des bouchons d’oreille et deux types de serre-tête (EAR1000 et Peltor Optime 98) sont montrés sur les Figure 17 et Figure 18a. La forme nominale des bouchons d’oreille passifs varie du cylindre droit à section circulaire constante ou variable (bouchon en mousse à comprimer, en mousse prémoulé à tige et prémoulé) à une forme épousant, dans l’ensemble, celle du canal auditif[3] (bouchon sur mesure). La géométrie des bouchons en mousse et prémoulés est plus ou moins modifiée lors de l’insertion dans le canal auditif selon la rigidité respective du matériau constituant le bouchon et celle des tissus de l’oreille externe. Les serre-têtes sont constitués de deux coquilles liées par un arceau de positionnement sur la tête, sous le menton, ou derrière la nuque, ou parfois liées à un casque de protection (casque de chantier, casque de bucheronnage…). Le système liant les deux coquilles permet d’exercer une force de serrage réglable. Chacune des coquilles est constituée d’un assemblage d’une coque plastique, contenant une mousse absorbante à cellules ouvertes, et remplissant totalement ou partiellement la cavité, ainsi que d’un coussin de confort qui est lié à la coquille par une contreplaque qui est soit clipsée à la coquille, soit montée en force. Bien souvent, un protecteur auditif de type coquille contient une seule enveloppe plastique, mais on peut parfois observer des protecteurs à double enveloppe (Figure 18b). Les protecteurs à double enveloppe procurent une atténuation sonore supérieure à celle d’un protecteur à simple enveloppe. Cependant, ceux-ci sont moins répandus, plus lourds et plus chers. Le coussin est conçu pour garantir à la fois le confort de l’usager et l’étanchéité acoustique entre la coque plastique et la tête. Il s’agit généralement d’une pièce de mousse, de forme annulaire, recouverte d’une gaine en polymère plus ou moins rigide. Les coussins des deux protecteurs étudiés par les chercheurs de l’équipe sont également munis de deux évents communiquant avec l’extérieur, qui leur permet de se dégonfler lorsque comprimés par la force de serrage. Le coussin du modèle EAR1000 (©3M) possède une gaine en polymère assez rigide et est attaché à la contreplaque au moyen d’un adhésif. Le coussin du PELTOR OPTIME 98 (©3M) est intégré directement à la plaque support et contient une lamelle de fluide insérée entre la mousse et la contreplaque. Il est important de noter que la gaine de polymère du modèle PELTOR OPTIME 98 est bien plus souple que celle du coussin EAR1000.

Lorsque le protecteur est couplé à l’oreille, le protecteur et les tissus de la tête se déforment simultanément et c’est en principe l’état déformé du système qui nous intéresse pour faire les calculs acoustiques plutôt que la géométrie nominale. Or, comment accéder à cette géométrie déformée ?
Lorsque l’oreille est occluse par un bouchon, les techniques classiques utilisées pour obtenir la géométrie du canal ne peuvent plus être utilisées et on doit avoir recours aux techniques d’imagerie médicale.
Benacchio et col ont proposé une méthode pour évaluer les déplacements des parois du canal auditif sur un participant à partir de l’analyse d’images IRM du canal ouvert et occlus par différents types de bouchons (Benacchio et al., 2019) (voir Figure 19). En fonction de la position sur l’axe du canal auditif, des déplacements de 1 à 2mm peuvent être induits par la présence du bouchon. L’importance de cette déformation sur le comportement acoustique du système n’a, à notre connaissance, pas fait l’objet d’études. Les modèles vibroacoustiques d’oreille avec bouchon de type moulé ou en mousse font plutôt l’hypothèse qu’au niveau géométrique, le canal ne se déforme pas lorsque le bouchon y est inséré. Ce dernier se déforme alors pour épouser la forme du canal ouvert. Pour les bouchons de type prémoulés (ex Ultrafit) qui se déforment de façon complexe, le problème de la détermination de cette géométrie reste entier (Gan et al., 2019). Notons que dans plusieurs modèles et pour éviter d’avoir à mailler le fluide externe, seule la partie du bouchon en contact avec le canal auditif est modélisée même si le bouchon n’est pas complètement inséré et sort de la conche. Le bouchon est alors supposé tronqué (Brummund et al., 2014a; Xu et al., 2021, 2022).
Quant aux travaux qui se sont intéressés aux protecteurs supra-auriculaires, la déformation des structures anatomiques (ex pavillon de l’oreille) et des tissus de la tête induite par le contact avec le coussin n’est jamais prise en compte. En fait, les modèles les plus avancés ne considèrent pas le pavillon ni la compression des tissus. La seule déformation prise en compte dans les travaux existants est celle du coussin de confort qui est comprimé par la force de serrage exercée par l’arceau du serre-tête qui assure le maintien sur la tête. La déformation réelle est complexe car le coussin a tendance à se bomber et l’écrasement n’est pas uniforme spatialement (Boyer, 2015 ; Boyer et al., 2015). En pratique, des études numériques ont montré que la géométrie du coussin déformé n’induit pas de grosses erreurs sur les calculs acoustiques. Ce dernier peut être considéré comme un tore de section rectangulaire d’épaisseur constante déterminée par la force de serrage.
Remarque 9 : L’insert en mousse dans un serre-tête antibruit est supposé garder sa forme nominale et épouser la forme de la coquille dans lequel il est placé. En pratique, du fait qu’il est très souple, sa forme exacte une fois inséré dans la coquille peut être modifiée mais demeure inconnue.

Fluide extérieur
Comme le fluide extérieur est considéré comme infini, l’utilisation de la méthode des EF nécessite de tronquer ce fluide et d’appliquer des conditions aux limites qui permettent de simuler le caractère infini du fluide pour les ondes acoustiques qui s’y propagent. Une approche plus performante consiste à circonscrire la tête avec un volume d’air convexe (typiquement un cube, un cylindre ou une sphère) sur lequel vient s’appuyer un domaine artificiel appelée couche parfaitement adaptée (Perfectly Matched Layer (PML) en anglais) (Bériot et Modave, 2020) (voir Figure 10). La taille de ce volume doit être choisie intelligemment pour ne pas augmenter inutilement le nombre de degrés de liberté du système lors de la discrétisation de ce volume. Un maillage réglé par exemple en éléments prismatiques ou hexaèdres de ce domaine artificiel dans l’épaisseur est également conseillé.
Matériaux et lois de comportement
Le problème vibroacoustique à résoudre ici fait intervenir des structures anatomiques (peau, cartilage, tissus mous , os, cerveau, fluide cérébrospinal, membrane tympanique, osselets, ligaments, tendons etc.), les constituants des protecteurs ainsi que des fluides (air extérieur, air contenu dans le canal auditif ou la cavité de l’oreille moyenne[4], air contenu dans le protecteur supra-auriculaire).
Tissus biologiques
Pour des excitations acoustiques de niveau crête inférieur à 150dB ou des stimulations solidiennes induites par ossivibrateurs, l’ensemble des matériaux constituant les tissus sont généralement supposés[5] se comporter comme des solides élastiques isotropes linéaires caractérisés par leurs propriétés élastiques, i.e le module d’Young, la masse volumique, le coefficient de Poisson et le facteur de perte. Certaines publications considèrent des propriétés viscoélastiques à travers un facteur de perte dépendant de la fréquence (Chang et al., 2016). Des exemples de propriétés sont fournies dans le Tableau 2. Notons que les propriétés des tissus sont accompagnées d’incertitudes importantes du fait de la grande difficulté de les caractériser et de leur variabilité inter-individuelle. Elles doivent donc être ajustées dans la phase de calibration du modèle.
| Es [MPa] | ρs [kg m-3] | νs [1] | ηs [1] | cf [m s-1] | |
| Cartilage | [1.60, 10.60] | [1000, 1160] | [0.26, 0.38] | [0.12,0.30] | – |
| Tissus mous (incluant la peau) | [0.20, 0.7] | [890, 1170] | [0.28, 0.50] | 3 . 10-5 f
[0.045, 0.1] |
– |
| Tissus mous (incluant le cartilage) | 7.2 | 1080 | 0.26 | 0.05 | – |
| Peau | 0.50 | 1100 | 0.40 | 0.10 | – |
| Os | [4000, 12000] | [1500, 1900] | [0.19, 0.48] | [0.01, 0.10] | – |
| Cerveau | 0.035 | 1000 | 0.45 | 3 . 10-4 f | – |
| Fluide cérébrospinal | – | 1000 | – | – | 1500 |
Un point crucial sur lequel insister est l’importance de la bonne connaissance des propriétés de la peau (qui est souvent combinée aux tissus mous dans les modèles) car c’est par elle que se fait le contact avec l’air du canal auditif et le protecteur. Il y a cependant une incertitude importante sur les valeurs de ses paramètres élastiques (module d’Young et coefficient de Poisson si on adopte un modèle élastique isotrope). La peau est généralement considérée comme quasi-incompressible donc avec un coefficient de Poisson proche de 0.5. La célérité des ondes de compression dans ce type de matériaux est relativement bien connue et est de l’ordre de 1400 à 1500 m s-1. Cette célérité dépend du module d’incompressibilité qui est lié au module d’Young et au coefficient de Poisson. La connaissance de l’un des deux paramètres est donc essentielle si on veut déterminer le second afin que la célérité soit de l’ordre de 1400à 1500 m s-1. Au niveau numérique le choix d’un coefficient de Poisson proche de 0.5 (ex 0.48, 0.49, 0.499, 0.4999) va imposer une valeur de module d’Young qui peut varier d’un facteur 1000. Cette incertitude a un très gros impact sur le calcul de la pression acoustique dans le canal auditif en particulier lorsque la conduction solidienne est prise en compte. Il est donc important d’avoir une bonne idée de l’ordre de grandeur du module d’Young de la peau en se basant sur des caractérisations ex-vivo en laboratoire ou des valeurs de la littérature. Ces valeurs devront être ajustées lors du processus de calibration du modèle. Notons que lorsque les matériaux sont quasi-incompressibles, des problèmes numériques peuvent survenir si seuls des degrés de liberté en déplacement sont utilisés pour les éléments finis. Il faut alors opter pour une formulation mixte en pression ou en déformation pour ces matériaux (Bathe, 1996).
Remarque 10 : Les propriétés de l’air et des tissus dépendent de la température. Les travaux de modélisation effectués jusqu’à présent considèrent généralement que cette température est la température ambiante (i.e autour de 20-24°). Ceci est pertinent lorsque le modèle simule des tests sur oreille ou tête artificielle (non chauffée). Par contre, quand on cherche à comparer les simulations avec des mesures sur sujets, cette hypothèse est questionnable. L’air contenu dans le canal auditif étant en contact avec les tissus qui sont à la température du corps humain (i.e 37°C) et avec l’extérieur à température ambiante, il existe un profil de température dans le canal qui devrait être en théorie pris en compte. En ce qui concerne les propriétés des tissus, il faudrait les caractériser à la température de 37° C et/ou les ajuster par un processus de calibration mesures/calculs. A notre connaissance l’effet de la température sur la pression acoustique dans le canal ouvert (et occlus) n’a jamais été étudié quantitativement dans la littérature.
Serre-tête
Composants plastiques
La coque et la contreplaque sont généralement des pièces en plastique dur (acrylonitrile butadiène styrène (ABS) ou polychlorure de vinyle (PVC)). La rotule qui permet d’attacher la coque et l’arceau est en caoutchouc. L’arceau est également en plastique souple mais n’est jamais modélisé en tant que tel d’un point de vue mécanique. Seul son effet mécanique statique est pris en compte à travers la compression du coussin (à la fois la géométrie déformée et les propriétés viscoélastiques qui dépendent du taux de compression). Tous ces composants sont considérés comme des solides élastiques isotropes caractérisés par leur masse volumique, leur coefficient de Poisson, leur module d’Young et leur facteur de perte structural.
| EAR-1000 | Peltor-Optime 98 | ||||
| Coquille | Contre-plaque | Rotule | Coquille | Contre-plaque | |
| Masse volumique [kg m-3] | 1200 | 1200 | 800 | 1040 | 1370 |
| Module d’Young [GPa] | 2.16 | 2.16 | 0.1 | 2.2 | 2.4 |
| Coefficient de Poisson [1] | 0.38 | 0.38 | 0.48 | 0.38 | 0.38 |
| Facteur de perte [1] | 0.05 | 0.05 | 0.5 | 0.05 | 0.05 |
Coussin de confort
Le coussin peut être modélisé par quatre approches de complexité croissante : « ressort équivalent dissipatif», « solide équivalent isotrope», « solide équivalent orthotrope» et « multi-domaines ». Chacune de ces approches a ses avantages et inconvénients. Dans tous les cas, le coussin est considéré comme un matériau viscoélastique dont les propriétés mécaniques varient en fonction du taux de compression qui lui est imposé par l’arceau, mais également en fonction de la température ambiante et de la fréquence.
Ressort équivalent dissipatif
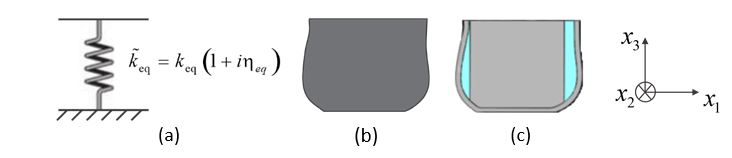
Le modèle le plus simple assimile le coussin à une condition de frontière de suspension mécanique de raideur [latex]k_{{\rm{eq}}}[/latex] en parallèle avec un amortisseur de type structural caractérisé par un facteur de perte [latex]\eta_{{\rm{eq}}}[/latex] (Figure 20a) et appliquée à l’interface coussin/contreplaque. La géométrie du coussin est dans ce cas-ci non représentée. Toutefois, afin de tenir compte du même volume de la cavité intérieure à la coquille, la partie basse de cette cavité (entourée par le coussin) doit être présente dans le modèle et ses frontières avec le coussin sont alors remplacées par une condition de mur rigide (vitesse particulaire normale nulle). Ainsi aucune transmission acoustique à travers le coussin n’est prise en compte. La suspension mécanique appliquée à la contreplaque se fait dans la direction de pompage du coussin (axe z dans les modèles). La caractérisation des paramètres [latex]k_{{\rm{eq}}}[/latex] et [latex]\eta_{{\rm{eq}}}[/latex] est détaillée dans (Boyer et al., 2015).
Solide équivalent isotrope
Le modèle de « solide équivalent » suppose que tous les domaines constituant le coussin, la gaine, la mousse, les poches d’air créées par l’écrasement du coussin et autres composants (comme la poche d’huile dans le cas du coussin du PELTOR-OPTIME-98) forment un seul et unique domaine solide supposé homogène et isotrope (voir Figure 20b). Ce modèle requiert seulement quatre paramètres mécaniques équivalents, à savoir : la masse volumique équivalente [latex]\rho_{{\rm{coussin}}}[/latex], le module d’Young équivalent [latex]E_{{\rm{coussin}}}[/latex], le coefficient de Poisson [latex]\nu_{{\rm{coussin}}}[/latex] et le facteur de perte structural équivalent [latex]\eta_{{\rm{coussin}}}[/latex], [latex]E_{{\rm{coussin}}}[/latex] et [latex]\eta_{{\rm{coussin}}}[/latex] étant dépendant de la fréquence et du taux de compression du coussin. Les deux paramètres [latex]E_{{\rm{coussin}}}[/latex] et [latex]\eta_{{\rm{coussin}}}[/latex] peuvent être déterminés avec une méthode inverse hybride expérimentale-numérique basée sur le modèle de Zener (Boyer, 2015 ; Boyer et al., 2015). Plus spécifiquement, dans un premier temps, une méthode expérimentale quasi-statique utilisant un QMA (Quasi-static Mechanical Analyzer) fournit la dépendance fréquentielle de la raideur équivalente du [latex]{k_{{\rm{coussin}}}}\left( {{f}} \right)[/latex] et [latex]{\eta_{{\rm{coussin}}}}\left( {{f}} \right)[/latex] en basses fréquences pour un taux de compression d’environ 10%. au taux de compression désiré avec [latex]f_0[/latex] la fréquence de résonance du système. Un modèle de Zener permet d’extrapoler ce comportement en plus hautes fréquences. Une méthode résonante est ensuite utilisée pour mesurer [latex]{k_{{\rm{coussin}}}}\left( {{f_0}} \right)[/latex] et [latex]{\eta_{{\rm{coussin}}}}\left( {{f_0}} \right)[/latex] au taux de compression désiré avec [latex]f_0[/latex] la fréquence de résonance du système. [latex]{k_{{\rm{coussin}}}}\left( {{f}} \right)[/latex] et [latex]{\eta_{{\rm{coussin}}}}\left( {{f}} \right)[/latex] sont obtenus en utilisant les valeurs [latex]{k_{{\rm{coussin}}}}\left( {{f_0}} \right)[/latex] et [latex]{\eta_{{\rm{coussin}}}}\left( {{f_0}} \right)[/latex] et la dépendance fréquentielle, supposée indépendante du taux de compression, déterminée à la première étape. [latex]{k_{{\rm{coussin}}}}\left( {{f}} \right)[/latex] dépend à la fois de [latex]{E_{{\rm{coussin}}}}[/latex] et du coefficient de Poisson équivalent [latex]{\nu_{{\rm{coussin}}}}[/latex] Ce dernier paramètre ne pouvant être mesuré directement, il est fixé à différentes valeurs entre 0 et 0.4. Pour [latex]{\nu_{{\rm{coussin}}}}[/latex] fixé ainsi qu’un taux de compression donné, [latex]{E_{{\rm{coussin}}}}[/latex] est obtenu par calibration d’un modèle EF simulant la méthode quasi-statique. [latex]{E_{{\rm{coussin}}}}[/latex] et [latex]{\nu_{{\rm{coussin}}}}[/latex] sont donnés par
Un exemple de valeurs de la raideur statique [latex]M_0[/latex] , de la limite en hautes fréquences de la raideur[latex]M_\infty[/latex] de l’exposant [latex]\alpha[/latex] et du temps de relaxation [latex]t_r[/latex] pour un taux de compression de 19.8% est fourni dans le Tableau 4 pour un coefficient de Poisson de 0.4 et une température de 22°C. D’autres valeurs sont fournies pour différents coefficients de Poisson pour les serre-têtes EAR1000 et Peltor Optime 98 dans la référence (Boyer et al., 2015). La méthode pour extraire ces paramètres pour d’autres taux de compression y est également décrite.
L’utilisation d’un tel modèle permet de tenir compte des déformations du coussin dans les différentes directions de l’espace autorisant ainsi une meilleure reproduction des couplages avec les autres domaines de la coquille. La transmission acoustique à travers les flancs du coussin est également possible. Cependant, ce modèle de coussin ne permet pas de capturer le bon comportement physique en transmission acoustique à travers le coussin dans certaines zones de fréquences. En particulier, un mode transverse du coussin parasite excité acoustiquement apparait dans la courbe d’atténuation de la coquille EAR-1000 créant une sous-estimation de cette atténuation. Lorsqu’artificiellement on n’excite pas les flancs du coussin dans le modèle, ce mode n’est plus excité et la prédiction de l’atténuation est grandement améliorée autour de la fréquence de résonance de ce mode. Cet artifice qui revient à négliger la transmission acoustique à travers les flancs du coussin est cependant discutable en moyennes fréquences car l’atténuation du coussin est alors proche de celle des autres composants de la coquille et un modèle plus élaboré est requis.
Solide équivalent isotrope transverse
Ce modèle est une amélioration du précédent. Il considère que le coussin se comporte mécaniquement de façon différente dans la direction de l’épaisseur notée [latex]x_3[/latex] et le plan [latex](x_1, x_2)[/latex] orthogonal à cette direction. Plus spécifiquement la raideur transverse peut être considérée plus élevée que celle dans l’épaisseur du fait du gonflement latéral du coussin lorsqu’il est comprimé. On parle de loi de comportement isotrope transverse. Le tenseur des déformations et de contrainte mécanique sont reliés par
où [latex]E_{x_1}[/latex] et [latex]E_{x_3}[/latex] sont les modules d’Young transverse et dans la direction [latex]x_3[/latex], [latex]{G_{{x_1}{x_2}}} = \frac{E_{x_1}}{2(1+\nu_{x_1x_2})}[/latex] et [latex]{G_{{x_1}{x_3}}}[/latex] sont les modules de cisaillement, [latex]{\nu_{{x_1}{x_2}}}[/latex] et [latex]{\nu_{{x_1}{x_3}}}[/latex] sont les coefficients de Poisson. [latex]E_{x_3}(f)[/latex] correspond à [latex]{E_{{\rm{coussin}}}}\left( f \right)[/latex] dans (2.1). Carillo (Carillo et al., 2018) considère [latex]{\nu _{{x_1}{x_2}}} = {\nu _{{x_1}{x_3}}} = \nu[/latex], [latex]{G_{{x_1}{x_3}}} = {G_{{x_1}{x_2}}}[/latex], [latex]{E_{{x_1}}}\left( f \right) = {E_{{x_3}}}\left( f \right) + h[/latex] où [latex]h[/latex] est une constante ajustée par méthode inverse par rapport à des mesures de IL. Le facteur de perte dans la direction [latex]z[/latex] est égal à [latex]{\eta _{{\rm{coussin}}}}\left( f \right)[/latex] dans (2.1). Le facteur de perte [latex]\eta_G[/latex] associé à [latex]{G_{{x_1}{x_2}}}[/latex] est également recalé par rapport aux mesure de IL. Pour l’EAR-1000, [latex]h=1[/latex] MPa et [latex]\eta_g=1[/latex].
Multi-domaines
Dans ce modèle chaque composant du coussin (gaine, mousse écrasée, poche d’huile dans le cas du PELTOR-OPTIME-98, poches d’air créées par l’écrasement du coussin) est modélisé (voir Figure 18a et Figure 20). Ce modèle qui détaille tous les domaines permet de tenir compte à la fois du comportement mécanique et du comportement acoustique du coussin. Il a pour inconvénients d’augmenter considérablement la complexité du modèle et donc le temps de calcul. De plus, il nécessite de caractériser finement chacun des constituants ainsi que leur couplage. Un tel modèle n’a jamais fait l’objet de publications.
Insert en mousse
L’insert en mousse dans la coquille est un matériau poreux à cellules ouvertes, généralement en polyuréthane, qui peut être décrit à l’échelle macroscopique comme un matériau diphasique comportant une phase fluide (l’air contenu dans les pores) et une phase solide (le squelette). Ces matériaux dissipatifs ont la propriété d’amortir le champ acoustique sous la coquille. Il existe différents modèles de ces matériaux. L’un des plus performants est celui de Biot-Johnson-Champoux-Allard (Allard et Atalla, 2009). Ce modèle nécessite cependant de bien décrire les couplages entre la coquille, la contreplaque et la mousse et à notre connaissance il n’a jamais été utilisé pour cette application. En fait des modèles plus simples où la mousse est assimilée à un fluide équivalent dissipatif ont été plutôt utilisés (Sgard et al., 2010b). Cette simplification origine du fait que l’insert est placé dans la coquille sans collage. Différents niveaux de complexité de modèles fluides équivalents existent dans la littérature. Le comportement acoustique du matériau dépend alors d’un certain nombre de paramètres macroscopiques, tels que la résistivité, sa porosité pour les modèles les plus simples (Delany et Bazley, 1970 ; Miki, 1990) et d’autres paramètres tels que la tortuosité et les longueurs caractéristiques visqueuse et thermique pour les modèles plus complexes (Champoux et Allard, 1991 ; Lafarge et Lemarinier, 1997). L’ensemble de ces paramètres peuvent être déterminés par des techniques de mesure directe ou indirecte (Olny, 1999). Pour l’insert en mousse du serre-tête EAR-1000, Sgard adopte un modèle de fluide équivalent « limp » à squelette rigide à 6 paramètres faisant intervenir la porosité [latex]\phi[/latex], la résitivité [latex]\sigma[/latex], la tortuosité [latex]\alpha_\infty[/latex], les longueurs caractéristiques visqueuse [latex]\Lambda[/latex] et thermique [latex]\Lambda'[/latex] et la masse volumique apparente du matériau [latex]\rho_1[/latex] (Allard et Atalla, 2009). Ces paramètres ont été identifiés à l’aide d’une technique de mesure indirecte acoustique utilisant le tube à ondes stationnaire et figurent dans le Tableau 5 (Sgard et al., 2010b).
Bouchons
Les bouchons d’oreille passifs sont constitués de matériaux variés. Les bouchons moulés sont généralement faits d’un matériau de type silicone ou en acrylique. Les bouchons prémoulés sont des assemblages de thermoplastique rigide (tige) et souple (tête du bouchon). Enfin les bouchons en mousse sont constitués d’un matériau poreux à cellules fermées en surface, comme une mousse à compresser avant insertion faite de PVC (ex EAR classic) ou de polyuréthane (ex 3M – 1100). Dans le cadre de la problématique vibroacoustique qui nous intéresse ici, seuls les bouchons moulés en silicone et en mousse à comprimer en PVC (3M classic) ont été étudiés (Sgard et al., 2010b, 2016). Dans ces travaux, le silicone et la mousse PVC sont considérés comme des matériaux isotropes viscoélastiques. Les propriétés mécaniques sont la masse volumique [latex]\rho _{\rm{b}}[/latex], le module d’Young [latex]E_{\rm{b}}[/latex], le coefficient de Poisson [latex]\nu _{\rm{b}}[/latex] et le facteur de perte structural [latex]\eta _{\rm{b}}[/latex]. [latex]E _{\rm{b}}[/latex] et [latex]\eta _{\rm{b}}[/latex] dépendent a priori de la fréquence et de la température. En principe les matériaux devraient être caractérisés à la température d’opération donc autour de 37°C si on veut représenter ce qui se passe dans l’oreille d’un sujet ou une ATF chauffée. Lorsque les modèles sont comparés à des mesures sur ATF non chauffée, c’est la température ambiante qui doit être considérée. Les trois paramètres mécaniques [latex]E_{\rm{b}}[/latex], [latex]\eta_{\rm{b}}[/latex] et [latex]\nu_{\rm{b}}[/latex] sont typiquement caractérisés en laboratoire avec par exemple un analyseur mécanique dynamique (DMA) ou un rigidimètre (QMA) ou alors tirés de la littérature. La masse volumique est obtenue par pesée. Dans le cas des travaux (Sgard et al., 2010b, 2016), les propriétés des bouchons en silicone ont été mesurées puis calibrées avec des mesures de perte par insertion. L’identification des propriétés du bouchon en mousse est plus délicate car une fois inséré dans le canal auditif, il se déforme et est précontraint radialement. Cela se traduit par une modification de sa densité et de son module d’Young. Une difficulté supplémentaire vient du fait que dans un canal auditif de forme réaliste, le bouchon ne se déforme pas de façon uniforme le long de son axe de symétrie puisque la section droite du canal auditif change au fur et à mesure qu’on se rapproche de la membrane tympanique. James a décrit cet effet de compression radiale par une déformation radiale (ou taux de compression radiale) [latex]\raise0.5ex\hbox{$\scriptstyle {{r_c} - {r_n}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{r_n}}$}[/latex] où [latex]r_c[/latex] représente le rayon du bouchon comprimé et [latex]r_n[/latex] son rayon nominal. Il a développé un dispositif expérimental pour mesurer le module d’Young et du facteur de perte dynamiques pour trois taux de compression radiale (6%, 18% et 30%) uniformément appliqués sur le pourtour du bouchon (James, 2006). Dans la littérature, lorsqu’un bouchon en mousse est inséré dans un canal auditif réaliste, un taux de compression équivalent basé sur la section la plus comprimée ou un rayon équivalent obtenu par [latex]\sqrt {{V_{EP,c}}/\pi {l_{EP}}}[/latex] où [latex]V_{EP,c}[/latex] est le volume du bouchon comprimé et [latex]l_{EP}[/latex] la longueur du bouchon est utilisé (Brummund et al., 2014a ; Carillo et al., 2021a ; Xu et al., 2021) et les valeurs de James sont interpolées linéairement. Notons qu’il est nécessaire de procéder à une phase de calibration en ajustant ces valeurs de façon à ce que les calculs soient au plus proche des résultats de mesures. A priori les bouchons en plastique ou thermoplastique rigide et souple peuvent être considérés comme élastiques, les propriétés étant tirées de la littérature. Le Tableau 6 donne des valeurs typiques de paramètres (indépendants de la fréquence ici) pour le bouchon en mousse EAR-classic et des bouchons en silicone « maison ».
| Es [MPa] | ρs[kg m-3] | νs[1] | ηs[1] | |
| Mousse EAR-classic
(30% taux de compression) |
0.1 | 220 | 0.1 | [0.1,0.5] |
| Silicone | [0.85,1.2] | [1050-1150] | 0.48 | [0.1,0.12] |
Fluides
L’air extérieur se comporte comme un fluide linéaire parfait. L’air contenu dans le canal auditif peut être également considéré de façon similaire ou comme un fluide dissipatif où des phénomènes de dissipation viscothermiques peuvent survenir. Lorsqu’on s’intéresse au champ de pression acoustique dans le canal, l’hypothèse de fluide parfait peut être suffisante. Par contre, si on cherche à déterminer comment circule l’énergie acoustique par bilan de puissances ou qu’il y a présence de fuites acoustiques[6], il est indispensable de prendre en compte ces effets dissipatifs (Carillo et al., 2020a). Dans le cas de l’hypothèse de fluide parfait, la densité [latex]\rho_0[/latex] et la célérité du son [latex]c_0[/latex] sont les deux paramètres clés. Dans le cas d’un fluide dissipatif, la dissipation peut être prise en compte de plusieurs façons (Kampinga, 2010 ; Kampinga et al., 2010). Parmi les plus populaires, l’approche la plus simple consiste à introduire un facteur de perte global pour le fluide noté [latex]\eta_f[/latex]. Dans ce cas, la célérité des ondes au carré [latex]c_0^2[/latex] est remplacée par [latex]c_0^2(1+i\eta_f)[/latex] et donc le nombre d’onde [latex]k=\frac{\omega }{c_0}[/latex] devient [latex]\frac{\omega }{{{c_0}}}\left( {1 - i\frac{{{\eta _f}}}{2}} \right)[/latex]. [latex]\eta_f[/latex] peut être calibré par l’utilisateur ou exprimé en fonction des paramètres du fluide comme [latex]\rho_0[/latex], les coefficients de viscosité traduisant les effets d’amortissement par cisaillement, et les effets de vibration et rotation des molécules, la conductivité thermique et le rapport des chaleurs spécifiques [latex]\frac{C_p}{C_v}[/latex].
Une seconde approche est basée sur le modèle LRF (low reduced frequency en anglais) qui décrit les effets viscothermiques associés à la propagation acoustique dans des guides d’onde dont les dimensions de la section droite sont inférieures à la longueur d’onde acoustique. Dans ce modèle les effets dissipatifs sont également intégrés via un nombre d’onde complexe mais cette fois ce dernier dépend également de la forme de la section droite du guide d’onde (ici, le canal auditif). La dernière approche, qui est également la plus couteuse en temps de calcul, est la description du fluide par les équations complètes linéarisées de Navier-Stokes[7] (modèle viscothermique complet). Des valeurs typiques des propriétés de l’air à température ambiante sont données dans le Tableau 7.
Conditions aux limites
Couplage entre le fluide du canal auditif et l’oreille moyenne
La membrane tympanique située à l’extrémité du canal auditif forme un angle oblique avec les parois du canal et n’est donc pas perpendiculaire aux fronts d’onde qui sont plutôt en incidence rasante. Elle est, de plus, conique et inhomogène dans sa constitution. Elle est excitée à la fois par la pression acoustique[8] dans le canal auditif mais également par les vibrations solidiennes transmises à la chaine ossiculaire via les parois de la cavité de l’oreille moyenne. La membrane peut donc rayonner acoustiquement dans le canal auditif. Lors d’une excitation acoustique et pour des fréquences inférieures à 6kHz, il est habituel de considérer que l’effet de l’oreille moyenne/interne peut être modélisé par une impédance acoustique à réaction localisée[9] distribuée sur la surface de la membrane. Au-delà de cette fréquence, le champ de pression acoustique varie significativement sur la membrane tympanique et la représentation par une impédance est discutable. La conséquence de cette représentation a également comme conséquence que la puissance acoustique moyennée sur une période d’une excitation sinusoidale est nécessairement positive et donc la membrane ne peut qu’absorber l’énergie acoustique dans le canal auditif. Cette impédance acoustique peut être mesurée sur des sujets, mesurée/calculée sur des oreilles artificielles (Luan et al., 2019) ou estimée à partir de modèles à constantes localisées (Hahn, 1985 ; Hudde et Engel, 1998c ; Kringlebotn, 1988 ; Shaw et Stinson, 1981 ; Stirnemann, 2011). Avec cette modélisation, le tympan ne peut que dissiper une partie de l’énergie incidente mais ne peut pas rayonner acoustiquement dans le canal. Pour une excitation solidienne, l’hypothèse d’impédance à réaction localisée est considérée comme valide en basses fréquences tant que la chaine ossiculaire ne résonne pas et n’induit pas un rayonnement acoustique de la membrane tympanique dans le canal auditif (Stenfelt et al., 2002, 2003 ; Stenfelt et Goode, 2005). Ces résonances se produisent typiquement entre 1 et 3kHz. Dans les modèles analytiques, une source de débit placée dans l’oreille externe peut être ajoutée pour représenter la contribution de l’oreille moyenne (Schroeter et Poesselt, 1986). Dans le cadre d’un modèle EF, prendre en compte cette contribution de la membrane tympanique peut se faire en modélisant de façon détaillée l’oreille moyenne/interne (voir section Oreille externe – tête sans protecteur).
Remarque 11 : Dans le cas d’un fluide viscothermique le couplage entre le fluide interne et la membrane tympanique est supposé adiabatique, les transferts de chaleur étant supposés négligeables (Carillo et al., 2020a).
Remarque 12 : En présence d’une excitation de mécanique qui sollicite la conduction osseuse, la condition d’impédance doit être réécrite pour tenir compte du mouvement structurel relatif du contour de la membrane et du fluide ( Suzuki et al., 1989). Kersten et coll propose une approche pour déterminer une vitesse équivalente moyenne du contour des parois du canal correspondant aux limites de la surface acoustique correspondant à la membrane tympanique (Kersten et al., 2024).
Couplage entre le fluide du canal auditif ouvert et le fluide extérieur
Dans plusieurs publications (Boyer et al., 2015 ; Brummund et al., 2014a, 2015 ; Carillo et al., 2018, 2020a ; Gaudreau et al., 2017 ; Viallet et al., 2013, 2014, 2015), l’effet du fluide extérieur, d’impédance caractéristique [latex]\rho_0 c_0[/latex], est décrit par une impédance acoustique spécifique de rayonnement [latex]\hat Z_r[/latex] appliquée à l’entrée du canal (Hudde et Engel, 1998a ; Pierce, 1994). L’entrée du canal est supposée se comporter comme un piston plan bafflé rayonnant dans un espace semi-infini. L’impédance [latex]\hat Z_r[/latex] pour un piston circulaire de rayon bafflé est donnée par (Kinsler et Frey, 2000)
| [latex]{\hat Z_r} = {\rho _0}{c_0}\left( {1 - \frac{{{J_1}\left( {2k{r_{EC}}} \right)}}{{k{r_{EC}}}} + i\frac{{{H_1}\left( {2k{r_{EC}}} \right)}}{{k{r_{EC}}}}} \right)[/latex] | (2.3) |
Où [latex]J_1[/latex] et [latex]H_1[/latex] dénotent respectivement la fonction de Bessel et de Struve d’ordre 1, [latex]k[/latex] désigne le nombre d’onde dans le fluide externe. Pour une excitation acoustique dans le fluide extérieur, la condition aux limites consiste à imposer une accélération normale qui dépend de la pression bloquée induite par l’onde incidente et de la pression dans le canal auditif à l’entrée de celui-ci et de l’impédance spécifique de rayonnement du piston.
avec [latex]\underline n[/latex] la normale pointant dans le fluide extérieur. Dans le cas où le plan de l’entrée du canal est dans un plan de normale [latex]\underline n_B[/latex] pointant dans le fluide situé dans le canal auditif, la pression bloquée [latex]\hat p_b[/latex] induite par une onde plane [latex]{\hat A_{inc}}{e^{ - i{{\underline k }_{inc}}.\underline x }}[/latex] incidente sur le plan d’entrée (voir Eq (2.6)) est donnée par :
| [latex]{\hat p_b}\left( {\underline x } \right) = {\hat A_{inc}}\left( {{e^{ - i{{\underline k }_{inc}}.\underline x }} + {e^{ - i{{\underline k }_{ref}}.\underline x }}} \right)[/latex] | (2.5) |
avec [latex]\underline k_{ref}[/latex] le vecteur d’onde de l’onde plane réfléchie par le baffle et [latex]{\underline k _{ref}}.{\underline n _B} = - {\underline k _{inc}}.{\underline n _B}[/latex] et [latex]{\underline k _{ref}}.{t} = - {\underline k _{inc}}.{t}[/latex], [latex]t[/latex] étant un vecteur tangent au plan du baffle. Pour une entrée du canal auditif dans le plan [latex]z=0[/latex] et une incidence normale à ce plan (i.e [latex]\underline n_B = \underline e_3[/latex], [latex]{\underline k _{inc}} = \left( {\underline k _{inc}^n.{{\underline n }_B}} \right){\underline n _B} = \left| {{{\underline k }_{inc}}} \right|{\underline e _3}[/latex], [latex]{\underline k _{ref}} = \left( {\underline k _{ref}^n.{{\underline n }_B}} \right){\underline n _B} = - \left| {{{\underline k }_{inc}}} \right|{\underline e _3}[/latex]), on a [latex]{\hat p_b}\left( {\underline x } \right) = 2{\hat A_{inc}}\cos \left( {kz} \right)[/latex] et en [latex]z=0[/latex], [latex]{\hat p_b}\left( {\underline x } \right) = 2{\hat A_{inc}}[/latex].
Dans des travaux plus récents, une région convexe du fluide extérieur entoure la tête et est directement en contact avec le fluide interne[10]. Les conditions de couplage de type acoustique-acoustique se résument à la continuité d’une part de la vitesse particulaire normale et d’autre part de la pression acoustique. Le fluide à l’intérieur du canal auditif est généralement le prolongement du fluide extérieur et il n’y a donc qu’un seuil maillage fluide. Le couplage est donc automatiquement assuré au niveau des nœuds du maillage du fluide. Si les deux maillages ont été faits indépendamment et les nœuds ne sont pas coïncidents, les conditions de continuité doivent être imposées par exemple à l’aide de multiplicateurs de Lagrange. Pour simuler la présence d’un fluide infini (condition de Sommerfeld), une couche parfaitement adaptée (PML) est couplée à l’enveloppe externe de la région convexe (voir Figure 10).
Remarque 13 : Dans le cas où le fluide du canal auditif est modélisé comme un fluide viscothermique complet, le couplage entre les fluides interne et externe est supposé adiabatique puisque les transferts de chaleur sont négligeables.
Remarque 14 : la même approche que pour la Remarque 12 peut être utilisée pour l’impédance de rayonnement dans le cas d’une excitation mécanique (Kersten et al., 2024). Dans ce cas, c’est la vitesse équivalente moyenne du contour des parois du canal correspondant aux limites de la surface acoustique de l’entrée du canal qui doit être calculée.
Couplage entre le fluide du canal auditif et les parois du canal auditif
A l’interface fluide du canal auditif/parois du canal auditif, pour un fluide interne parfait, les conditions de couplage de type élasto-acoustique se résument d’une part à la continuité des vitesses normales du fluide et des parois et d’autre part à la continuité des tractions s’exerçant dans le fluide et sur les parois.
Remarque 15 : Dans le cas où le fluide du canal auditif est modélisé comme un fluide viscothermique complet, la première condition est remplacée par la continuité du vecteur vitesse particulaire acoustique et du vecteur vitesse de la paroi. De plus, les parois du canal auditif sont supposées isothermes puisque le corps humain est à température constante.
Couplage entre le fluide du canal auditif et le protecteur auditif
Dans le cas du serre-tête, c’est l’air contenu dans la coquille qui en contact avec l’air du canal auditif. On se retrouve dans la situation de la section Couplage entre le fluide du canal auditif ouvert et le fluide extérieur.
Dans le cas d’un bouchon en contact parfait[11] avec les parois du canal auditif, le couplage s’effectue au niveau de l’interface air/bouchon. Les conditions de couplage de type élasto-acoustique sont identiques à celles de la section Couplage entre le fluide du canal auditif et les parois du canal auditif. Si le contact n’est pas parfait, des fuites acoustiques peuvent survenir. Dans ce cas, l’air dans la fuite est en contact à la fois avec le bouchon et avec l’air de part et d’autre du bouchon. On se retrouve donc dans la situation des sections Couplage entre le fluide du canal auditif ouvert et le fluide extérieur et Couplage entre le fluide du canal auditif et les parois du canal auditif.
Couplage entre le fluide extérieur et le protecteur auditif
À l’interface entre le protecteur[12] et le fluide extérieur les conditions de couplage sont identiques à celles de la section Couplage entre le fluide du canal auditif et les parois du canal auditif. Dans le cas d’une excitation acoustique dans le fluide extérieur, il faut tout de même se rappeler que la pression acoustique est la pression acoustique totale résultant de la pression acoustique incidente et de la pression diffractée par la présence de la tête et du protecteur.
Des conditions de couplage simplifiées peuvent également être adoptées. Par exemple, des auteurs négligent le rayonnement acoustique du protecteur dans le fluide externe (Brummund et al., 2014a, 2015 ; Carillo et al., 2021a ; Viallet et al., 2013, 2014, 2015). Dans le cas d’une excitation acoustique cela se traduit par le fait que la traction s’exerçant sur le protecteur est égale à [latex]- {\hat p_b}\underline n[/latex] où [latex]\hat p_b[/latex] est la pression bloquée (voir section Méthode des éléments finis de frontière-Principe ) alors que dans le cas d’une excitation solidienne, la traction s’exerçant sur le protecteur est égale à 0 (condition aux limites libres).
Couplage entre le protecteur auditif et les tissus biologiques
Les conditions de couplage sont de type élastique-élastique et traduisent la continuité des déplacements et des tractions.
Dans le cas du serre-tête, le coussin est en contact avec les tissus mous de la tête autour de l’oreille mais également avec le pavillon de l’oreille. Cependant à notre connaissance, les travaux passés n’ont jamais considéré le couplage mécanique pavillon/coussin probablement parce que les zones de contact sont difficiles à évaluer. A fortiori, l’effet de ce couplage sur l’atténuation des serre-têtes n’a jamais été étudié. Le pavillon n’est donc pas modélisé et l’interaction mécanique entre serre-tête et tissus est donc supposée se produire au niveau de l’interface coussin/peau. Les seuls travaux sur la modélisation de l’atténuation de serre-tête intégrant un couplage avec des tissus (synthétiques en silicone) considèrent de plus que cette interface est plane et que le contact est parfait (Gaudreau et al., 2017 ; James, 2006).
Dans le cas des bouchons, la partie insérée dans l’oreille est en contact avec la conche (cas des bouchons sur mesure) et les parois du canal auditif. Comme mentionné dans la section Oreille externe – tête avec protecteur, la difficulté ici réside dans la détermination des zones de contact entre le bouchon et l’oreille. Le couplage peut être pris en compte de façon exacte avec les conditions de continuité élastique-élastique ou bien, dans le cas d’une excitation acoustique de façon simplifiée en utilisant des conditions aux limites d’impédance (Viallet, 2014). Dans le cas d’un canal auditif artificiel en métal, de simples conditions aux limites cinématiques de type déplacement imposé à 0 dans les trois directions peuvent être utilisées (Viallet et al., 2013).
Si le couplage mécanique protecteur-tissus n’est pas parfait, i.e s’il y a présence de fuites acoustiques, il est alors nécessaire de considérer des conditions de couplage acoustique et élasto-acoustique additionnelles comme mentionné dans la section Couplage entre le fluide extérieur et le protecteur auditif.
Il s’agit ici des couplages résultant de l’assemblage de composants différents. Pour les bouchons, il est question essentiellement de la tige et de la partie en mousse (bouchons en mousse prémoulés à tige) ou en thermoplastique (bouchons prémoulés). A notre connaissance, seuls des bouchons constitués d’un seul matériau (3M classic, push-in sans la tige, ou bouchon moulé) ont pour l’instant été étudiés (Sgard et al., 2019). Pour les serre-têtes, on parle de la coque en plastique, la rotule en caoutchouc, l’arceau, la contreplaque, le coussin (mousse, air, gaine), la poche d’huile (ou gel) éventuelle et l’insert en mousse. Les travaux passés considèrent un couplage élastique-élastique parfait[13] entre la coque, la rotule, la contreplaque et le coussin. Le couplage élastique-élastique de l’arceau avec la rotule n’est pas pris en compte en tant que tel puisque l’arceau n’est jamais modélisé d’un point de vue dynamique. Il est supposé simplement jouer un rôle statique qui se traduit par l’écrasement du coussin et potentiellement un rôle acoustique de diffraction. L’insert en mousse est généralement modélisé comme un fluide équivalent. On a donc un couplage de type élasto-acoustique sur les zones de contact entre l’insert et la coque/contreplaque et de type acoustique-acoustique sur les interfaces insert-fluide interne à la coquille.
Conditions d’excitation
Excitation acoustique
L’excitation acoustique est typiquement modélisée par
- une onde plane en incidence oblique définie par son amplitude [latex]\hat A_{inc}[/latex] et les angles sphériques [latex]\phi_{inc}[/latex] et [latex]\theta_{inc}[/latex][14]
| [latex]{\hat A_{inc}}{e^{ - i{{\underline k }_{inc}}.\underline x }}[/latex] | (2.6) |
avec [latex]{\underline k _{inc}} = \left( {k\sin {\theta _{inc}}\cos {\phi _{inc}},k\sin {\theta _{inc}}\sin {\phi _{inc}},k\cos {\theta _{inc}}} \right)[/latex] le vecteur d’onde de l’onde incidente et [latex]\underline x[/latex] la position du point de calcul
- un monopole d’amplitude [latex]\hat A[/latex] placée en un point [latex]\underline x_0[/latex]
- un champ diffus pouvant être représenté par une superposition d’ondes planes d’amplitudes égales et non corrélées se propageant librement dans toutes les directions. Dans ce cas il suffit de faire un calcul avec N ondes planes provenant de tout l’espace et de sommer de façon incohérente les amplitudes de la réponse obtenue pour chacune de ces N ondes planes pour obtenir la réponse au champ diffus. Par exemple pour le module de la pression au carré en champ diffus en un point [latex]\underline x[/latex] donné, noté [latex]|\hat p_d\left( \underline x \right) |^2[/latex], on aura :
où [latex]\hat p_k(\underline x)[/latex] est le résultat du calcul au point [latex]\underline x[/latex] pour l’onde plane d’angle d’incidence ([latex]\phi_{inc,k}[/latex], [latex]\theta_{inc,k}[/latex]). L’amplitude de l’onde plane incidente peut être choisie de telle façon que le module de la pression incidente au carré résultant de la superposition des N ondes planes soit égal à 1. Dans ce cas, [latex]{\hat A_{inc,k}} = \frac{1}{4\pi}[/latex] Si on adopte une répartition uniforme des ondes planes, le nombre N peut être élevé. Une façon de réduire ce nombre est de considérer la version intégrale de l’équation (2.7) et d’utiliser des points de Gauss distribués sur une sphère de rayon 1m pour calculer cette intégrale. En fonction de la fréquence maximale de la bande de fréquence, un nombre de points entre 16 et 32 peut s’avérer suffisant. On aura alors
où [latex]{\hat p_{\phi ,\theta }}\left( {\underline x } \right)[/latex] est le résultat du calcul au point [latex]\underline x[/latex] pour l’onde plane d’angle d’incidence [latex](\phi, \theta)[/latex].
Excitation solidienne
Quant à l’excitation mécanique qui représente traditionnellement un ossivibrateur, elle est modélisée comme une force ponctuelle ou répartie (cas où la source mécanique a une impédance mécanique faible devant celle de l’élément excité) (voir Eq(1.12)b), ou un déplacement imposé ponctuel ou réparti (cas où la source mécanique a une impédance mécanique grande devant celle de l’élément excité). (voir Eq(1.12)d). Cette excitation est généralement appliquée sur la peau à l’emplacement de la mastoïde ou du front, qui correspond à la position de l’ossivibrateur lors de tests sur sujets humains.
Calcul des indicateurs
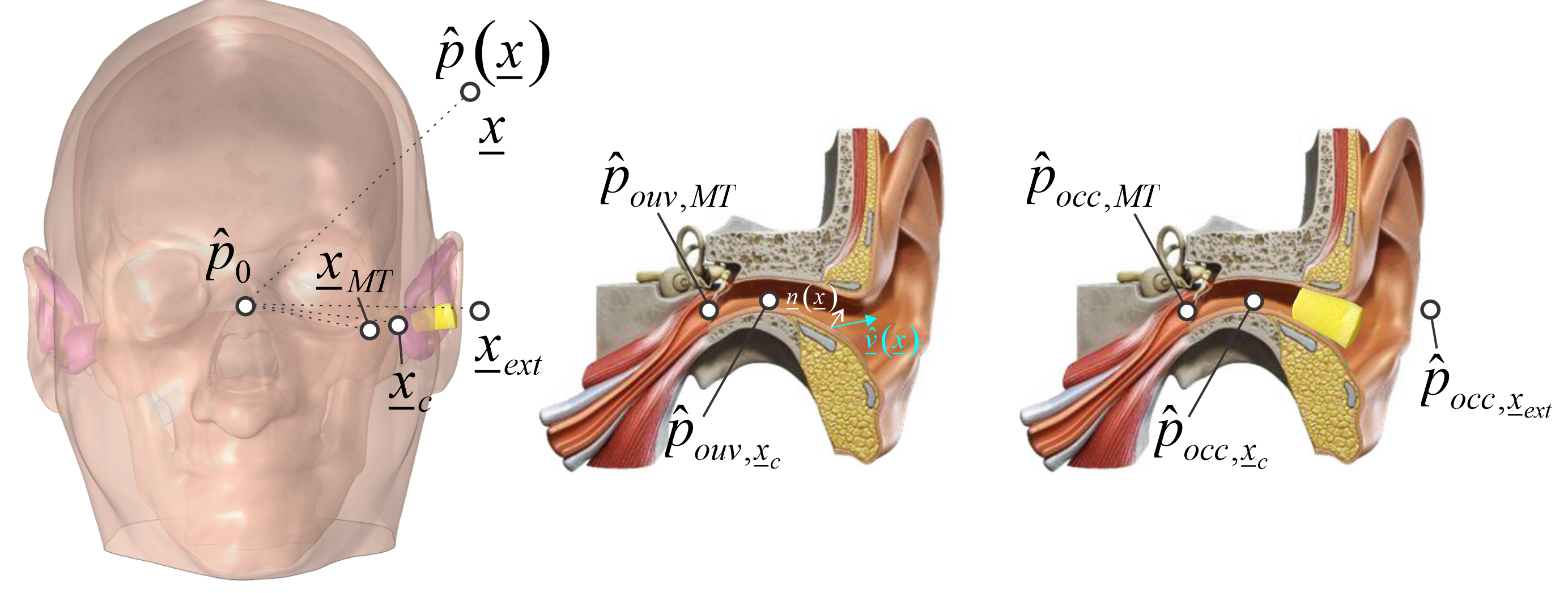
Dans cette section, on présente les expressions des indicateurs acoustiques et vibratoires utilisés dans le domaine de la protection auditive. La Figure 21 illustre les notations adoptées pour les indicateurs.
Niveaux de pression acoustique
Le niveau de pression acoustique en un point [latex]\underline x[/latex] d’un milieu fluide est donné par
| [latex]{L_{p,\underline x }} = 20\log \left( {\frac{{\left| {\hat p\left( {\underline x } \right)} \right|}}{{\sqrt 2 {p_{ref}}}}} \right)[/latex] | (2.9) |
Pour le niveau de pression acoustique à la membrane tympanique [latex]\partial {\Omega _{MT}}[/latex], on peut le calculer en un point spécifique de cette dernière ou effectuer une moyenne spatiale sur la surface de cette dernière. On a alors :
Atténuation acoustique
L’atténuation acoustique peut être évaluée à partir de la perte par insertion (IL) et l’affaiblissement sonore (NR). Un certain nombre d’autres indicateurs peuvent être définis qui relient IL et NR sont également intéressants à calculer (Nélisse et al., 2015). Les indicateurs qui suivent sont définis pour une excitation acoustique externe mais certains d’entre eux peuvent également avoir un sens pour une excitation solidienne (ex [latex]NR^*[/latex], [latex]TF_{canal}[/latex], [latex]TF'_{canal}[/latex]).
Perte par insertion [latex]IL[/latex]
| [latex]IL = {L_{p,ouv,MT}} - {L_{p,occ,MT}}[/latex] | (2.11) |
avec [latex]{L_{p,ouv,MT}}[/latex] et [latex]{L_{p,occ,MT}}[/latex] les niveaux de pression acoustique à la membrane tympanique en oreille ouverte et occluse résultant d’une excitation acoustique.
Affaiblissement sonore [latex]NR[/latex]
| [latex]NR = {L_{p,0}} - {L_{p,occ,MT}}[/latex] | (2.12) |
avec [latex]L_{p,0}[/latex] le niveau de pression acoustique au centre de la tête qui existerait sans la présence de la tête.
Affaiblissement sonore [latex]NR^*[/latex]
| [latex]NR^* = {L_{p,occ,{{\underline x }_{ext}}}} - {L_{p,occ,{{\underline x }_c}}}[/latex] | (2.13) |
avec [latex]{L_{p,occ,{{\underline x }_{ext}}}}[/latex] et [latex]{L_{p,occ,{{\underline x }_c}}}[/latex] les niveaux de pression acoustique en un point extérieur [latex]\underline x_{ext}[/latex] généralement à proximité du protecteur et en un point [latex]\underline x_c[/latex] du canal auditif occlus par le protecteur.
Fonction de transfert de l’oreille ouverte [latex]TFOE[/latex]
| [latex]TFOE = 20\log \left( {\left| {\frac{{{{\hat p}_{ouv,MT}}}}{{{{\hat p}_0}}}} \right|} \right) = {L_{p,ouv,MT}} - {L_{p,0}}[/latex] | (2.14) |
Fonction de transfert de l’oreille ouverte [latex]TF_{canal}[/latex]
| [latex]T{F_{canal}} = 20\log \left( {\left| {\frac{{{{\hat p}_{ouv,{{\underline x }_c}}}}}{{{{\hat p}_{ouv,MT}}}}} \right|} \right) = {L_{p,ouv,{{\underline x }_c}}} - {L_{p,ouv,MT}}[/latex] | (2.15) |
Fonction de transfert de l’oreille ouverte [latex]TF_{canal}'[/latex]
| [latex]TF_{canal}' = 20\log \left( {\left| {\frac{{{{\hat p}_{occ,{{\underline x }_c}}}}}{{{{\hat p}_{occ,MT}}}}} \right|} \right) = {L_{p,occ,{{\underline x }_c}}} - {L_{p,occ,MT}}[/latex] | (2.16) |
Remarque 16 : Lorsque l’excitation du canal est acoustique, que la conduction osseuse est négligeable et qu’on ne considère que les ondes propagatives dans le canal, [latex]T{F_{canal}} = TF_{canal}'[/latex] au point [latex]\underline x_c[/latex] à une fréquence donnée (Chan et Geisler, 1990 ; Gilman et Dirks, 1986). Dans le cas d’une excitation solidienne où intervient la conduction osseuse, les valeurs de [latex]T{F_{canal}}[/latex] et [latex]TF_{canal}'[/latex] dépendent de la distribution de vitesse des parois du canal et de celle de la surface médiale du bouchon et en fonction de la position du point [latex]\underline x_c[/latex],[latex]TF_{canal}[/latex] peut être différente de [latex]TF_{canal}'[/latex] .
Fonction de transfert de l’oreille occluse[latex]TF_{ext}'[/latex]
| [latex]TF_{ext}' = 20\log \left( {\left| {\frac{{{{\hat p}_{occ,{{\underline x }_{ext}}}}}}{{{{\hat p}_0}}}} \right|} \right) = {L_{p,occ,{{\underline x }_{ext}}}} - {L_{p,0}}[/latex] | (2.17) |
Remarque 17 : On a les relations utiles suivantes
| [latex]IL = NR + TFOE[/latex] | (2.18) |
| [latex]NR = NR^* + TF_{canal}' - TF_{ext}'[/latex] | (2.19) |
Effet d’occlusion objectif
| [latex]OE = L_{p,occ,MT}^s - L_{p,ouv,MT}^s[/latex] | (2.20) |
avec [latex]L_{p,occ,MT}^s[/latex] et [latex]L_{p,ouv,MT}^s[/latex] les niveaux de pression acoustique à la membrane tympanique en oreille ouverte et occluse résultant d’une excitation solidienne.
Débit acoustique
Il peut être intéressant de calculer le débit acoustique imposé par une frontière d’un domaine solide [latex]\partial \Omega_s[/latex] (p.ex les parois du canal auditif et de la face médiale du bouchon) vibrant avec une vitesse [latex]\underline{\hat v}[/latex] à un fluide (p.ex le canal auditif). On a alors :
| [latex]\hat w = \int_{\partial {\Omega _s}} {\underline {\hat v} \left( {\underline x } \right).\underline n \left( {\underline x } \right)dS\left( {\underline x } \right)}[/latex] | (2.21) |
où [latex]\underline n[/latex] est la normale à l’interface [latex]\partial \Omega_s[/latex] pointant dans le fluide.
Vitesse quadratique moyenne d’un solide
La vitesse quadratique moyenne de la phase solide dans la direction i (i=1,2,3) est donnée par :
[latex]\underline{\hat v}[/latex] est le vecteur vitesse au point [latex]\underline x[/latex] du milieu solide et [latex]\hat v_i[/latex] est la composante du vecteur vitesse dans la direction [latex]i[/latex].
Vitesse quadratique normale moyenne d’une surface
La vitesse quadratique moyenne de la phase solide normale est donnée par :
Puissances échangées entre un solide et un fluide
La puissance échangée à l’interface [latex]\partial \Omega_s[/latex] entre un domaine solide et un fluide est donnée par:
où [latex]\hat p[/latex] est la pression acoustique dans le fluide. Si la normale pointe du fluide vers le domaine solide alors [latex]{\Pi _{ech,f - s}} > 0[/latex] signifie que c’est le fluide qui transfère de la puissance au solide.
Puissance échangées entre deux solides
La puissance échangée à l’interface entre deux domaines solides s1 et s2 est donnée par :
où [latex]\underline{\underline \sigma}[/latex] représente le tenseur des contraintes dans l’un des solides.
Puissance dissipée dans un solide
La puissance dissipée dans un solide est donnée par :
où [latex]\underline{\underline \varepsilon }[/latex] représente le tenseur des déformations dans le solide.
Puissance dissipée dans un fluide
Un fluide dissipatif peut être décrit par un facteur de perte structural [latex]\eta_f[/latex] qui est associé soit aux effets thermiques soit aux effets visqueux. Dans le premier cas, c’est la raideur ou compressibilité du fluide qui est liée au facteur [latex]\rho_f c_f^2[/latex] qui devient à valeur complexe sous la forme [latex]\rho_f c_f^2(1+i\eta_f)[/latex]. Plus spécifiquement, c’est la célérité du son dans le fluide qui est supposée complexe telle que [latex]\hat c_f^2 = c_f^2\left( {1 + i{\eta _f}} \right)[/latex] et [latex]\rho_f[/latex] est supposée à valeurs réelles. Dans le second cas, la densité du fluide [latex]\hat \rho_f[/latex] et la célérité du son [latex]\hat c_f[/latex] sont supposées toutes les deux complexes avec [latex]{\hat \rho _f} = {\rho _f}\left( {1 - i{\eta _f}} \right)[/latex] et [latex]\hat c_f^2 = c_f^2\left( {1 + i{\eta _f}} \right)[/latex] mais [latex]{\hat \rho _f}\hat c_f^2[/latex] est réel. Le nombre d’onde défini par [latex]{\hat k_f} = \frac{\omega }{{{{\hat c}_f}}}[/latex] est égal à [latex]{\hat k_f} = \frac{\omega }{{{c_f}{{\left( {1 + i{\eta _f}} \right)}^{\frac{1}{2}}}}} \approx {k_f}\left( {1 - i\frac{{{\eta _f}}}{2}} \right)[/latex] pour de faibles facteurs de perte. Dans le premier cas, la puissance dissipée dans le fluide est donnée par :
| [latex]{\Pi _{diss,f}} = - \frac{1}{2}\int_{{\Omega _f}} {\Re \left( {\frac{\omega }{{i{\rho _f}c_f^2\left( {1 + i{\eta _f}} \right)}}{{\left| {\hat p} \right|}^2}} \right)dV}[/latex] | (2.27) |
Dans le second, on a :
On peut également obtenir cette puissance indirectement en écrivant un bilan de puissance pour le système fluide étudié, c’est-à-dire que la somme des puissances échangée entre le fluide et ses frontières et de la puissance dissipée dans le fluide est nulle.
Maillage
Le maillage des différents domaines doit être suffisamment fin pour capturer leur géométrie mais également pour résoudre les variations spatiales des champs acoustiques et vibratoires dans les différents domaines jusqu’à une fréquence donnée. Une estimation de la taille maximale de l’élément est obtenue en imposant qu’il y ait un nombre minimal d’éléments pour capturer la longueur d’onde du phénomène physique se produisant dans le milieu. Pour des problèmes de couplage fluide-structure, il est usuel de considérer comme critère initial de maillage 4 à 6 éléments par longueur d’onde en fonction du degré d’interpolation de l’élément choisi[15] et de la physique considérée. Pour l’acoustique linéaire où un seul type d’onde de compression peut exister, la longueur d’onde est simplement [latex]\frac{c_0}{f}[/latex]. Dans un milieu solide infini où à la fois des ondes de compression et de cisaillement peuvent coexister, on peut prendre la longueur d’onde la plus faible (celle de cisaillement [latex]\frac{c_s}{f}[/latex], où [latex]c_s[/latex][16] est la célérité des ondes de cisaillement dans un solide 3D infini). De façon alternative si le milieu solide est principalement excité en compression, on peut prendre la longueur d’onde correspondante [latex]\frac{c_p}{f}[/latex] où [latex]c_p[/latex][17] est la célérité des ondes de compression. Dans le cas d’un milieu solide avec des conditions aux limites, les ondes de compression et de cisaillement peuvent se combiner pour former d’autres types d’ondes (flexion, onde de surface de type Rayleigh, etc.) mais en général on ne connaît pas a priori le type d’onde qui s’y propage. Dans ce cas, un critère initial basé sur par exemple la longueur d’onde de cisaillement peut être utilisé. Une fois les domaines maillés avec ces critères préalables, il est impératif de faire une étude de convergence où le maillage est successivement raffiné jusqu’à ce que l’indicateur d’intérêt converge à la fréquence considérée. Certains logiciels d’EF ont des procédures de maillage adaptatif qui permettent de raffiner le maillage là où cela est nécessaire.
On voit ainsi que le maillage dépend de la fréquence. En principe, on pourrait donc à chaque fréquence refaire un maillage du domaine. Le temps d’assemblage des matrices élémentaires et de résolution du système matriciel augmente donc avec la fréquence. Pour des géométries complexes, le temps passé dans l’étape de maillage peut excéder ce temps d’assemblage et de résolution. De plus, il faut être sûr que la solution a convergé et donc pour chaque fréquence il faudrait procéder à un raffinement du maillage pour vérifier que ce soit effectivement le cas. En pratique, on décompose souvent la bande de fréquences de calcul en plusieurs sous bandes et pour chacune d’entre elle on construit un maillage en utilisant le critère précédent avec [latex]f[/latex] la fréquence maximale de la sous-bande considérée. On vérifie que la solution a convergé sur cette bande de fréquences en raffinant le maillage correspondant puis on passe à l’autre bande et ainsi de suite.
En général, on utilise des éléments solides tridimensionnels pour les domaines solides et fluides. La topologie est soit tétraédrique notamment dans le cas des structures anatomiques de forme complexe, ou héxaèdrique lorsque la géométrie s’y prête (ex certaines éléments du serre-tête) et des éléments d’ordre 2 (éléments quadratiques) sont préférés. Certaines structures anatomiques comme la membrane tympanique peuvent être modélisées par éléments surfaciques de coque.
Remarque 18 : La PML doit être maillée en éléments prismatiques avec un minimum de 8 éléments de taille identique dans la direction de l’épaisseur.
Remarque 19 : Lorsque le fluide est considéré thermo-visqueux complet, des précautions doivent être prises au niveau du maillage. En particulier, les parties du fluide en contact avec le domaine solide (couches limites) doivent être maillées plus finement.
Résolution
Le système matriciel obtenu après discrétisation des équations élasto-acoustiques du problème dans le domaine fréquentiel (Eq(1.19)) est du type [latex]\left[ {\hat A\left( \omega \right)} \right]\left[ {\hat X\left( \omega \right)} \right] = \left[ {\hat B\left( \omega \right)} \right][/latex] où [latex]\left[ {\hat X} \right][/latex] et [latex]\left[ {\hat B} \right][/latex] sont respectivement la matrice contenant les vecteurs solutions et les vecteurs second membre. Ce système peut être résolu à chaque fréquence avec des algorithmes numériques multiples directs ou itératifs[18] exploitant le caractère creux des matrices et le calcul parallèle. Parmi les algorithmes directs, mentionnons MUMPS, PARDISO, SPOOLES.[19] et pour les solveurs itératifs GMRES, FGMRES, QMR, BiCGStab, CGS, TFQMR[20]. Notons que ces derniers sont plus rapides, permettent de résoudre des problèmes de très grandes dimensions mais sont moins précis et stables numériquement que les précédents. Ils dépendent également du type de préconditionneur utilisé. En fonction du type de système matriciel (symétrique, hermitien, non symétrique, rectangulaire) certains solveurs sont davantage adaptés.
Une fois la solution obtenue par le solveur, il faut s’assurer que l’indicateur d’intérêt est convergé. Un indicateur global où une quantité est intégrée sur un volume ou sur une surface (ex vitesse quadratique moyenne, puissance acoustique, etc.) converge plus vite qu’un indicateur local comme le champ de pression acoustique ou de déplacement. La convergence est souvent évaluée de façon visuelle en comparant l’évolution fréquentielle (ou temporelle) des indicateurs obtenus pour le maillage initial et celui raffiné. En fonction d’une tolérance fixée par l’utilisateur sur l’amplitude et la position des accidents fréquentiels (résonances/anti-résonances) de cet indicateur, on décide si le maillage initial est suffisant ou nécessite d’être raffiné davantage. Des techniques récentes utilisant des éléments finis de type « p », où la taille des éléments est déterminée pour que l’erreur sur la solution soit inférieure à un seuil donné permettent d’éviter le processus de raffinement successif du maillage pour vérifier la convergence (Bériot et al., 2016 ; Bériot et Gabard, 2019).
Exemples de comparaison mesures/calcul
Dans cette section, on présente de façon succincte quelques exemples de résultats de modèles EF de différente complexité pour prédire l’atténuation acoustique (IL, NR) et l’effet d’occlusion (EO) de protecteurs auditifs. Ces modèles ont été évalués par rapport à des mesures sur des bancs expérimentaux spécialement développés pour valider les modèles, sur des ATF ou sur des groupes de sujets humains. Les détails de ces contributions peuvent être trouvées dans les références suivantes des auteurs (Brummund, 2014b ; Carillo et al., 2018, 2021b ; Luan, 2021, 2022 ; Viallet et al., 2014, 2015 ; Xu, 2021, 2022).
Atténuation
Bouchon
La Figure 22 montre l’atténuation de bouchons cylindriques en silicone moulés dans un canal auditif cylindrique comportant une épaisseur de silicone représentant la peau et placé dans une tête artificielle. Après des étapes de caractérisation en laboratoire et de calibration des propriétés des matériaux, les résultats de simulation en rouge sont en accord avec ceux des mesures pour les deux configurations de systèmes bouchon / canal auditif testées. Le dispositif expérimental et les modèles 2D axisymétriques associés utilisés pour le canal auditif ouvert et occlus sont représentés sur la Figure 23.
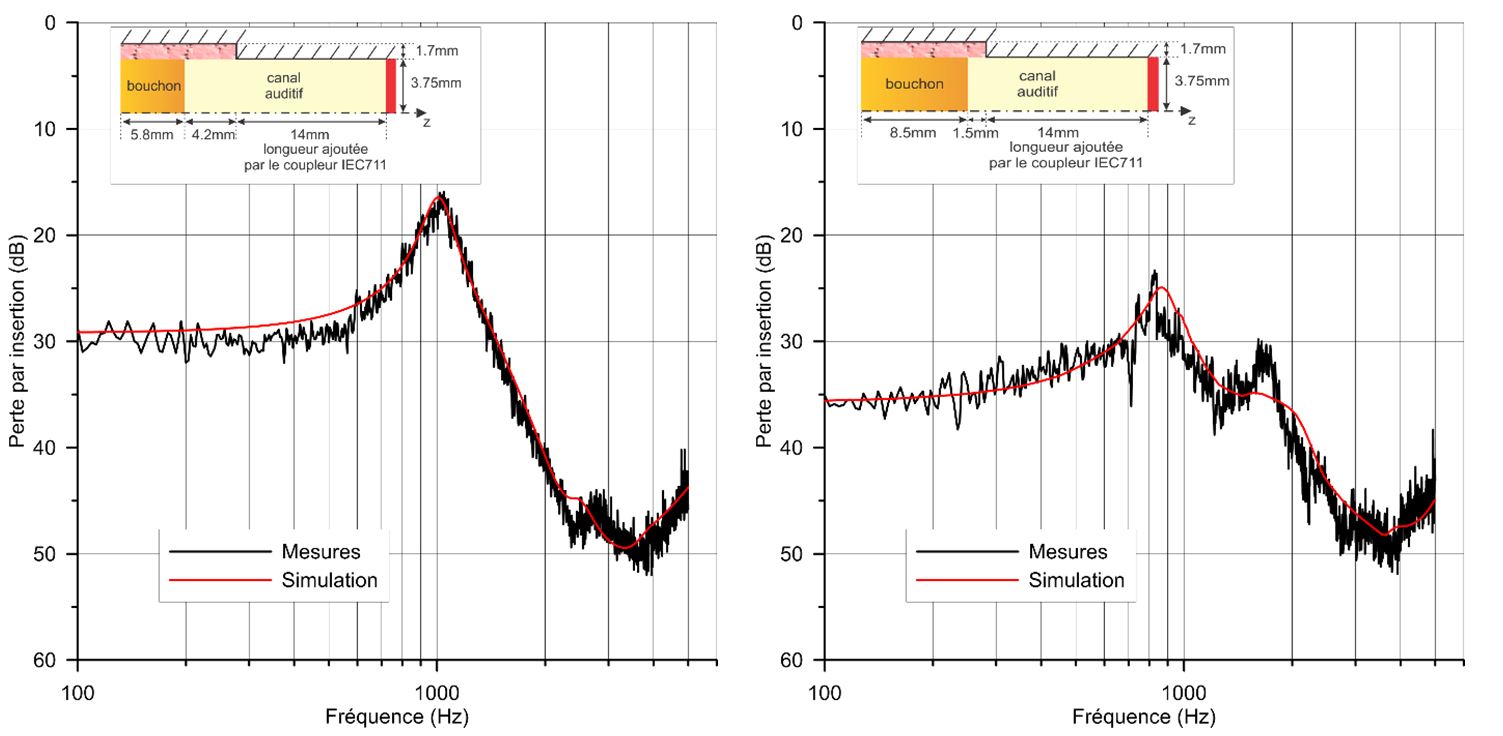
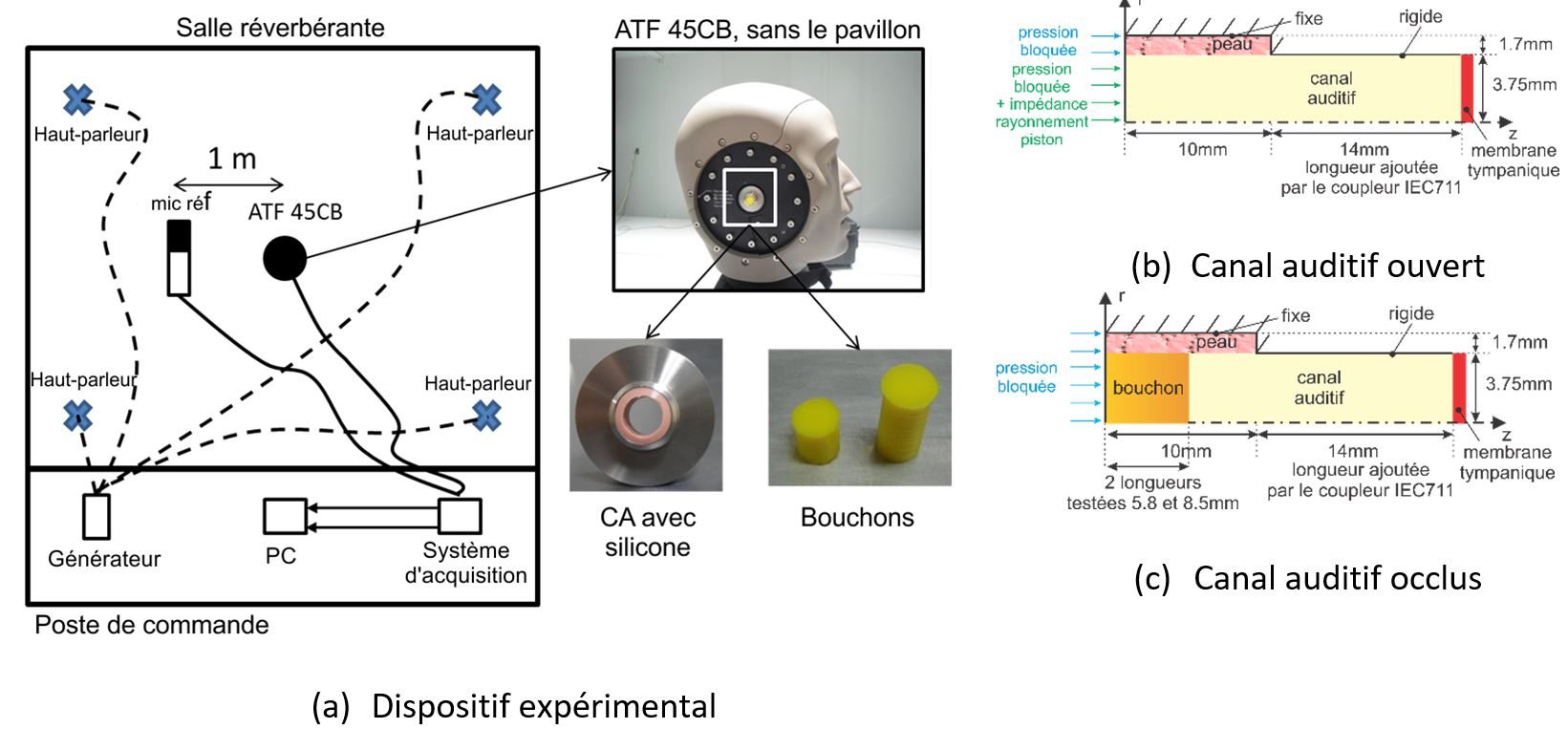
Des différences mineures apparaissent autour de 2 kHz pour le bouchon de 8,5 mm et 3 kHz pour le bouchon de 5,8 mm, possiblement en raison d’un amortissement mal estimé. Dans les deux cas, en l’absence de fuites, la perte par insertion est plate jusqu’à la première fréquence de résonance autour de 1 kHz pour le bouchon de 5,8mm et de 800 Hz pour le bouchon de 8,5mm. Au-delà de cette fréquence, le IL augmente progressivement. Comme attendu, un bouchon plus long a une perte par insertion plus grande en particulier en basses fréquences. La comparaison de ces résultats avec le cas où la peau artificielle est enlevée du canal auditif artificiel (Viallet et al., 2013) montrent l’importance de considérer la peau pour prédire l’atténuation des bouchons.
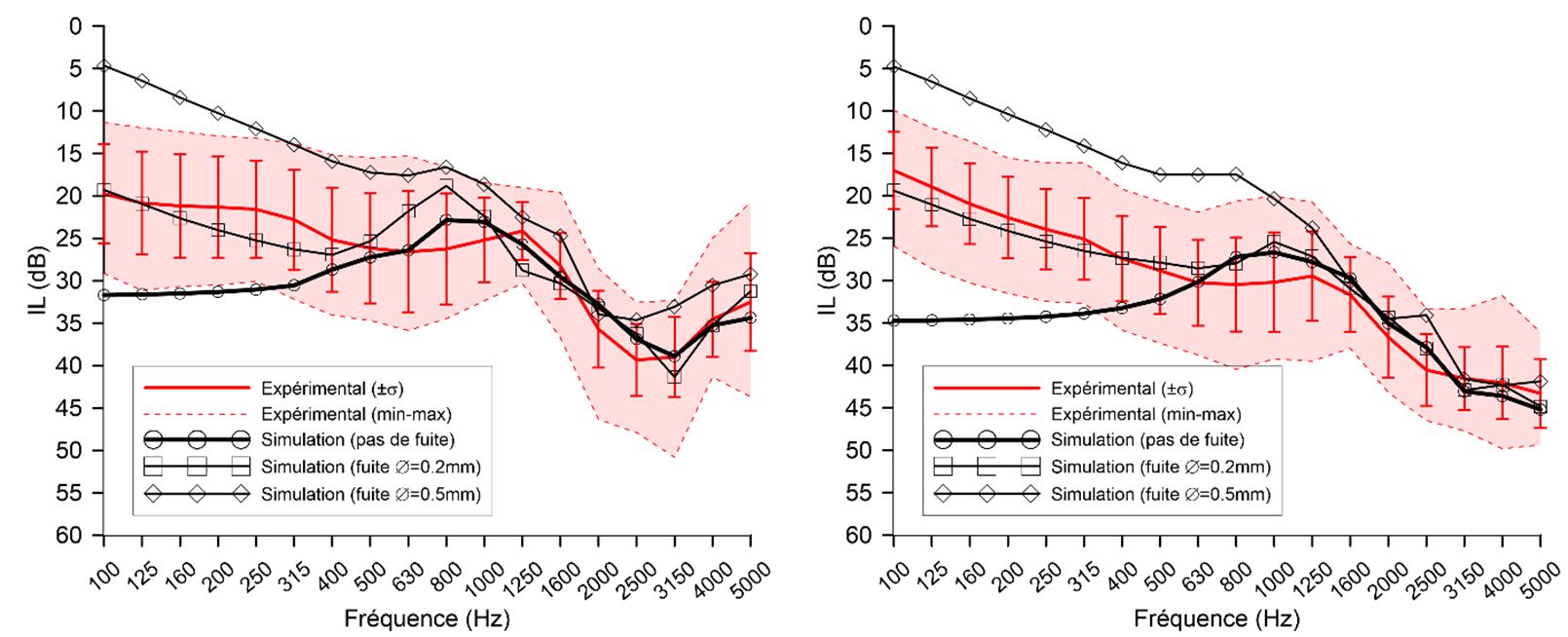
Un deuxième résultat provient de la comparaison calculs/mesures en tiers d’octave avec la méthode MIRE sur 29 sujets humains normo-entendants pour un bouchon moulé en silicone (Figure 25a) et un bouchon en mousse (Figure 25b) pour des insertions optimales du bouchon dans le canal (pas de fuite) et non optimales (présence de fuites de diamètre 0,2 mm et 0,5 mm). Le calcul est basé sur un modèle axisymétrique simplifié qui intègre la présence de tissus et de fuites potentielles. Le modèle occlus par les deux types de bouchons est représenté sur la Figure 24. Les longueurs insérées sont respectivement de 11,7 mm et 11,3 mm et correspondent aux profondeurs d’insertion moyennes mesurées sur des sujets humains.
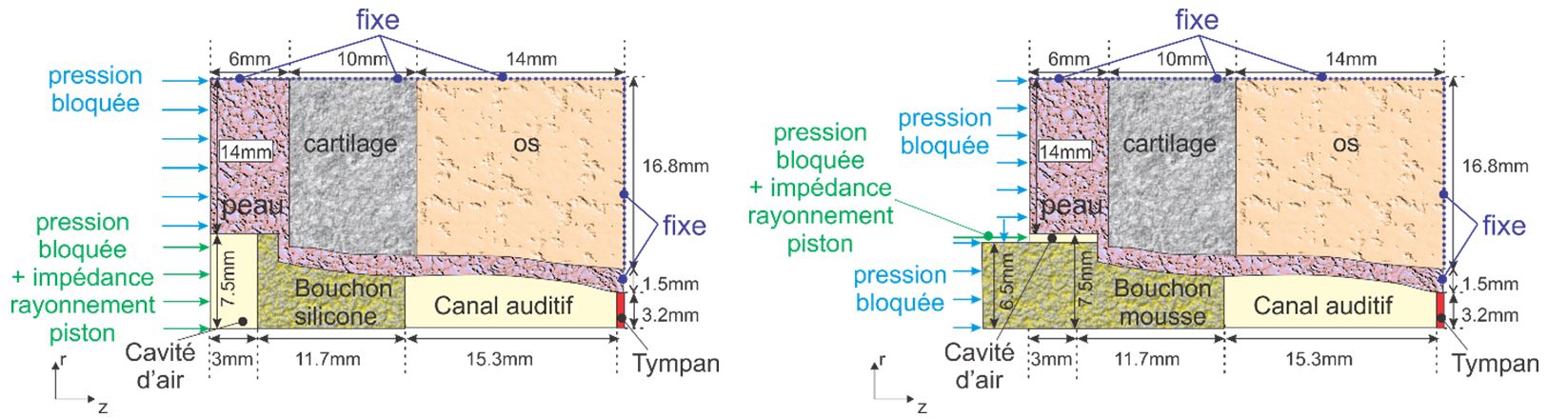
Pour le cas sans fuite, on constate que les simulations et mesures sont en bon accord excepté en basses fréquences. En dehors de cette zone, les prédictions suivent les moyennes expérimentales avec des différences locales plus ou moins importantes (de 1 à 5 dB au pire) et se situent toujours dans la région de la moyenne ± un écart type. Pour les fréquences inférieures ou égales à 1 kHz, la présence d’une fuite, même de faible taille, réduit considérablement l’atténuation. La réduction s’accroît encore lorsque le diamètre de la fuite augmente. Dans cette zone de fréquences, la gamme de variation obtenue entre le cas sans fuite et les deux cas avec fuites, couvre la zone de variation expérimentale relativement importante issue des mesures sur sujets humains. Cela indique que la présence de fuites peut expliquer, en partie, la grande variabilité des pertes par insertion mesurées sur sujets humains en dessous de 1 kHz. Au-dessus de 1 kHz, l’effet des fuites devient relativement faible et la variabilité interindividuelle de l’atténuation expérimentale peut plutôt s’expliquer par la variabilité géométrique des canaux auditifs (ici, sans pavillon) et, dans une moindre mesure, par l’effet de la variabilité des propriétés mécaniques des tissus.
Serre-tête
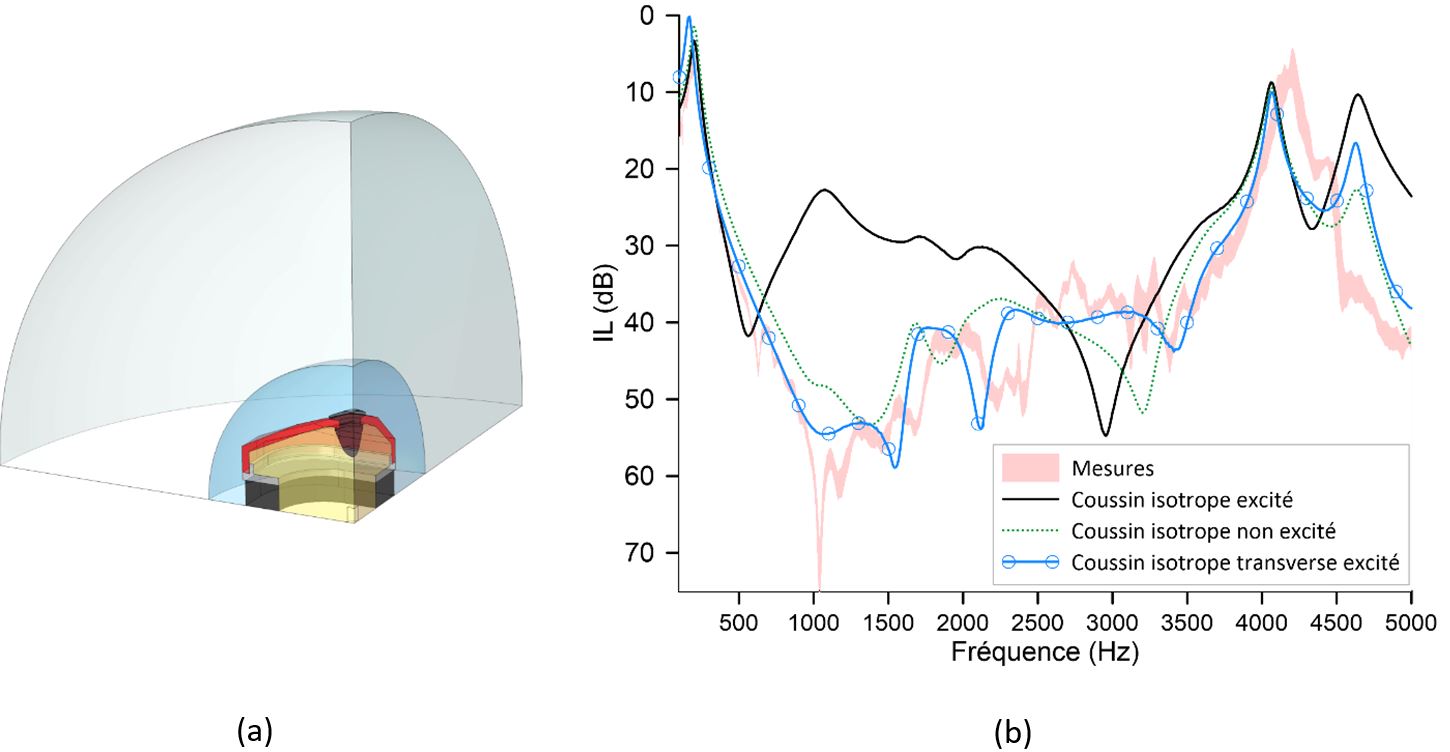
Plusieurs modèles EF du serre-tête commercial (EAR-1000 ©3M) de complexité croissante ont été développés par les auteurs (Boyer, 2015 ; Boyer et al., 2015 ; Carillo et al., 2018). Le modèle EF du système considéré ici est représenté sur la Figure 26a. Dans cette configuration, le serre-tête repose sur un baffle rigide et est excité par une onde plane en incidence normale. L’insert en mousse à l’intérieur de la coquille n’est pas modélisé. Trois modèles de coussin de confort sont étudiés : solide équivalent isotrope dont les parois latérales externes sont soit (i) excitées acoustiquement (trait noir plein) soit (ii) non excitées (trait rouge pointillé) et (iii) solide équivalent isotrope transverse dont les parois latérales externes sont excitées acoustiquement (ligne bleue continue avec des cercles). Les propriétés équivalentes du coussin isotrope transverse ont été préalablement calibrées. La Figure 26b illustre l’avantage d’utiliser un mode solide équivalent isotrope transverse pour le coussin par rapport à un modèle isotrope en comparant les atténuations sonores prédites et mesurées (perte par insertion (IL)) du serre-tête dans une configuration simplifiée. Alors que le IL mesuré (zone grise) est largement sous-estimé par le modèle de coussin isotrope excité en raison d’un mode transverse parasite du coussin, ne pas considérer l’excitation acoustique des parois latérales du coussin isotrope améliore l’IL prédit même si cette hypothèse est physiquement discutable. D’autre part, le modèle isotrope transverse excité offre un meilleur accord entre la simulation et la mesure car le mode coussin parasite est décalé vers des fréquences plus élevées.Afin de s’affranchir de la difficulté de modélisation du coussin de confort du serre-tête EAR-1000, Luan a remplacé le coussin de confort original par un coussin en silicone aux propriétés connues (matériau monophasique, isotrope et viscoélastique). Il a également fabriqué une ATF simplifiée destinée à faciliter la modélisation du système et également étudier les chemins de transmission solidiens (voir section Double protection). Le NR de l’EAR-1000 couplé à cette ATF simplifiée a ensuite été mesuré dans des conditions de champ diffus (voir Figure 28a 2 panneaux de gauche). Le modèle EF associé est décrit sur la Figure 27a. Dans le modèle, le coussin en silicone est considéré isotrope et ses parois latérales sont excitées. La Figure 27b compare les résultats de mesure et de simulations correspondantes. On constate que l’accord est excellent et on capte donc bien le comportement en transmission du système à la fois à travers la coquille mais également le coussin. Ceci confirme que pour mieux appréhender le NR ou le IL du serre-tête EAR-1000 avec le coussin de confort original, il est nécessaire d’améliorer la modélisation de ce dernier même si un modèle isotrope transverse permet de s’approcher des mesures.
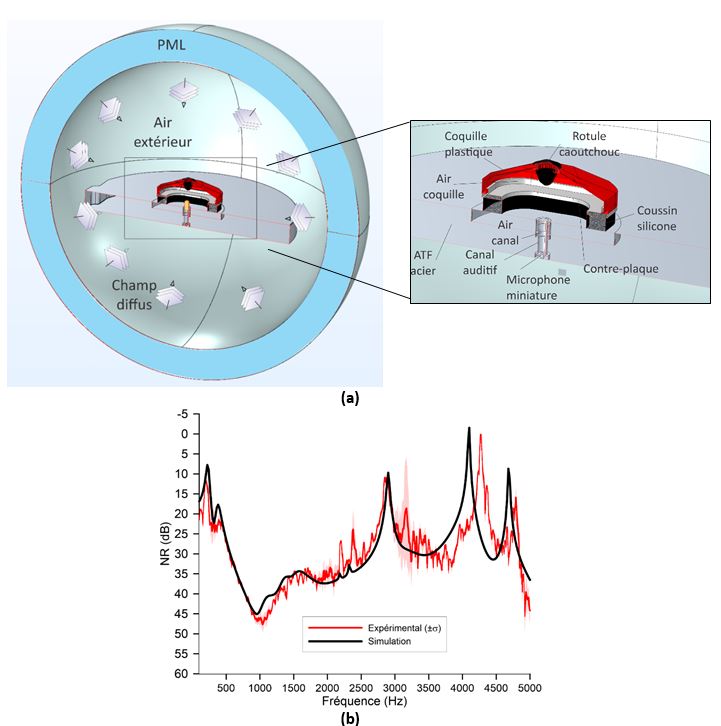
Double protection
Les auteurs ont proposé un modèle EF pour comprendre le comportement vibro-acoustique d’un système de double protection constitué d’un serre-tête commercial (EAR-1000 ©3M) modifié et d’un bouchon en silicone moulé. Le développement de ce modèle a été guidé par une analyse expérimentale des chemins de transfert à travers un tel système (Luan et al., 2021). Ce modèle est évalué par comparaison avec des mesures en chambre réverbérante (excitation par champ diffus) sur une ATF simplifiée constituée d’un cylindre en acier percé en son centre d’un trou cylindrique à section circulaire représentant le canal auditif d’une ATF commerciale Figure 28a. La terminaison arrière du canal auditif est rigide acoustiquement et comporte un microphone miniature Knowles pour mesurer la pression acoustique à l’intérieur du canal. Cette ATF simplifiée a été développée afin de faciliter la modélisation et réduire les incertitudes sur la connaissance des paramètres du modèle.
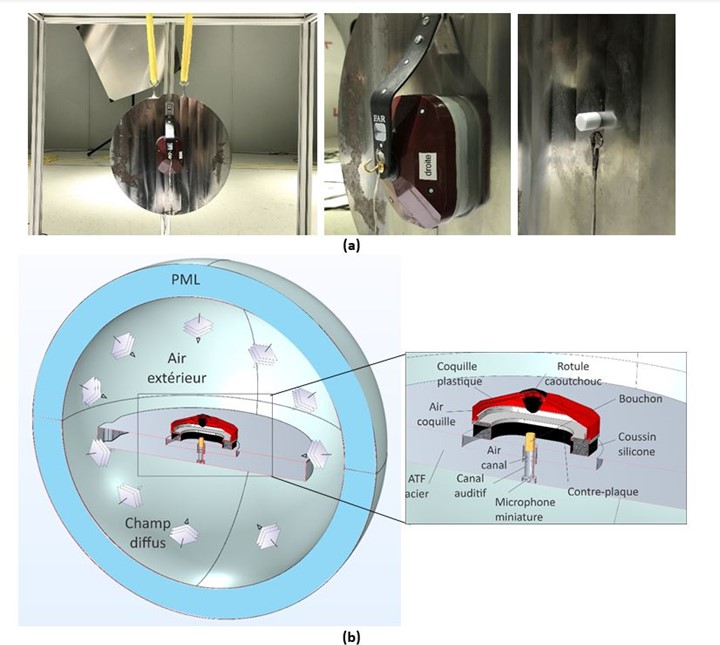
Le modèle EF correspondant est représenté sur la Figure 28b. Grâce à une analyse par bilans de puissances échangées entre les différents composants du système, le modèle permet d’expliquer pourquoi l’atténuation du bouchon diminue de façon significative dans une zone de fréquence qui s’étend sur plusieurs octaves lorsqu’il est couplé à un serre-tête. La Figure 29 compare les résultats de mesures et de calcul pour le NR du bouchon avec et sans coquille. Notons qu’en amont, les modèles de chaque protecteur considéré séparément ont été calibrés en se basant sur des mesures de IL associées. On voit que le modèle est capable de reproduire la diminution d’atténuation du bouchon lorsque ce dernier est porté dans une configuration de double protection. Celle-ci s’explique par une contribution importante au niveau de pression dans le canal auditif du chemin de transfert solidien à travers le coussin de la coquille, la peau synthétique de l’ATF et le bouchon (Luan, 2021).
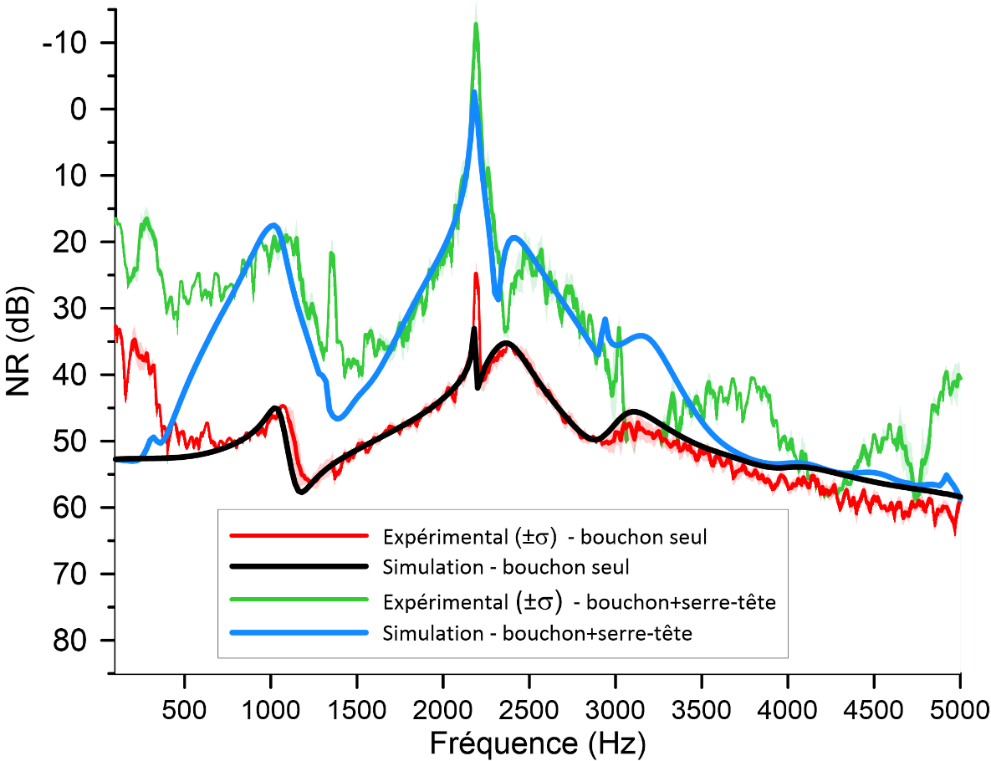
Effet d’occlusion
On s’intéresse à présent à l’effet d’occlusion objectif de bouchons induit par une excitation solidienne. On simule cet effet d’occlusion avec une variété de modèles EF tronqués individuels d’oreille externe et complet incluant la tête.
Dans le premier exemple, la Figure 30 compare l’effet d’occlusion objectif généré par un bouchon en mousse inséré à une profondeur moyenne (environ 10mm) dans le canal auditif pour une excitation par ossivibrateur sur la mastoide ipsilatérale et (i) mesuré par Reinfeldt et col (Reinfeldt et al., 2013) sur 20 sujets humains (ii) calculé avec un modèle tronqué adapté de Brummund et col (Brummund et al., 2014a) (voir Figure 16a) et (iii) calculé avec un modèle complet de tête de Xu et col (Xu et al., 2021, 2022) (voir Figure 16c). Au-dessus de 250Hz, les résultats des deux modèles (tronqué et complet) sont en accord avec les résultats expérimentaux et reproduisent correctement la diminution de l’effet d’occlusion expérimental avec la fréquence. Cette diminution s’explique par la modification de l’impédance acoustique vue par les parois du canal qui est gouvernée par les effets inertiel du canal auditif en oreille ouverte et par les effets de compressibilité en oreille occluse (Carillo et al., 2020b). Au-dessous de 250Hz, des différences importantes entre calcul et mesures peuvent être observées pour le modèle tronqué. Ces différences ont souvent été attribuées à des problèmes d’étanchéité acoustique entre le bouchon et les parois du canal auditif. La Figure 30 indique qu’un modèle complet de tête permet de réduire ces différences. Les écarts entre modèle tronqué et complet pourraient être expliqués par le rayonnement acoustique des tissus externes de la tête dans le canal auditif, qui ne sont pas pris en compte dans le modèle tronqué. Un modèle de tête complet permet donc de mieux rendre compte et gagner en compréhension des phénomènes physiques réels. Notons que dans les deux modèles EF, la condition aux limites d’impédance à réaction localisée au niveau de la membrane tympanique (et celle au niveau de l’entrée du canal dans le cas du modèle tronqué de l’oreille ouverte) ne tient pas compte du mouvement des parois du canal auditif. La prise en compte de ce mouvement peut également contribuer à expliquer les différences entre simulations et mesure, l’effet d’occlusion simulé étant diminué en dessous de 250Hz, lorsque les conditions d’impédance prennent en compte le mouvement relatif du fluide et des parois des canal (Kersten et al., 2024).
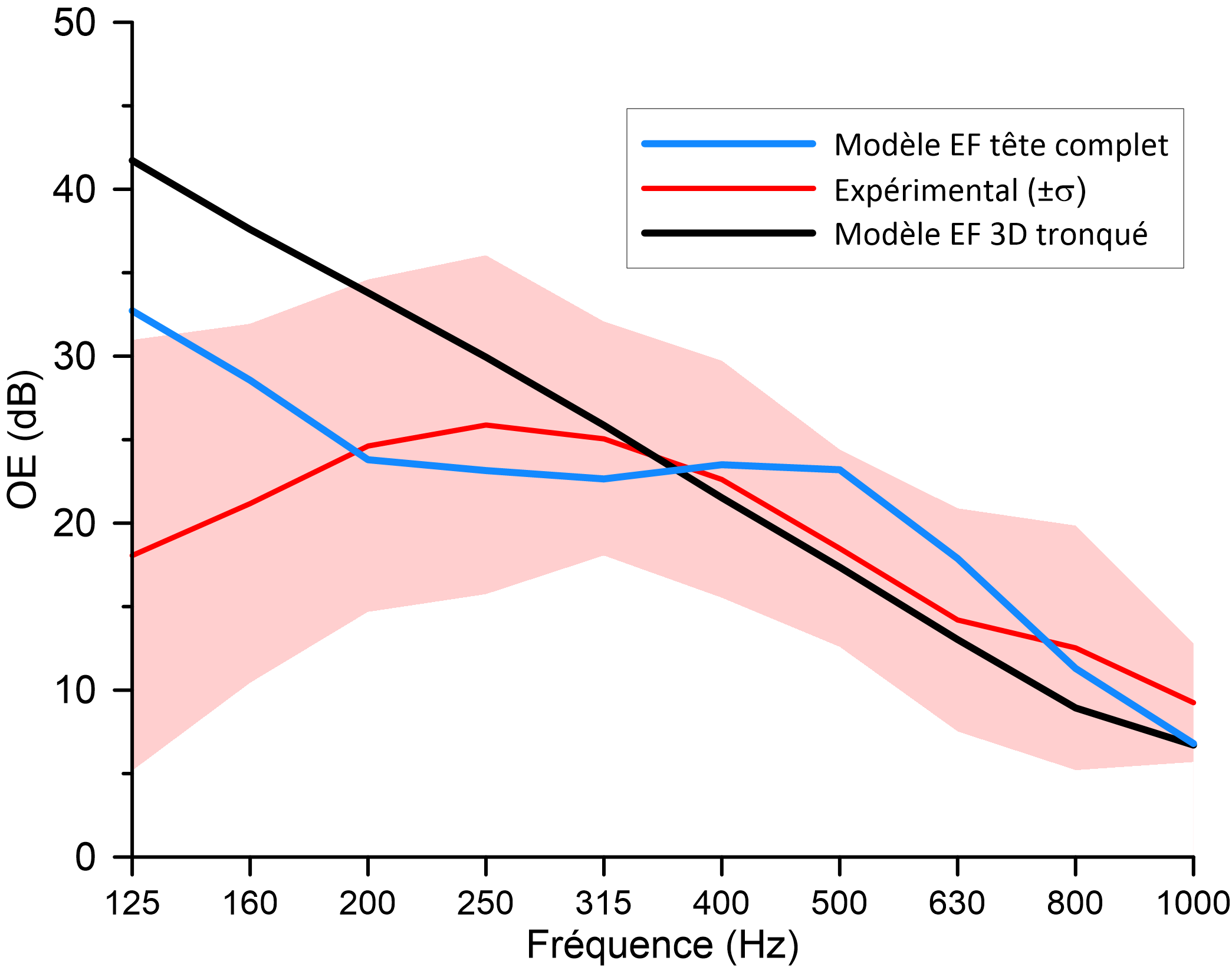
Dans le deuxième exemple, la Figure 31b montre l’effet d’occlusion objectif mesuré par Brummund et col (Brummund et al., 2015) sur 37 sujets humains munis de bouchons en mousse ou en silicone insérés à une profondeur moyenne dans le canal auditif, pour une excitation par ossivibrateur sur la mastoide ipsilatérale et calculé avec un modèle tronqué adapté 2D axisymétrique (Carillo et al., 2021a) (voir Figure 31a). La Figure 31b indique que les effets d’occlusion simulés à l’aide du modèle EF axisymétrique 2D sont en bon accord avec les données expérimentales. En dessous de 250 Hz, cependant, les simulations surestiment légèrement la mesure car elles ne tiennent pas compte du rayonnement acoustique de la tête dans le canal auditif ouvert. En moyenne, les bouchons d’oreille en silicone induisent un effet d’occlusion supérieur de 8 dB à celui des bouchons d’oreille en mousse. Comprendre l’origine de cette différence est d’un grand intérêt pour développer potentiellement des bouchons d’oreille qui atténuent le phénomène en modifiant leur comportement vibro-acoustique inhérent. En fait, la vitesse volumique imposée par la surface médiale du bouchon d’oreille (mousse et silicone) domine de loin la contribution de la paroi du canal auditif comme le montre la courbe « bouchon d’oreille » à impédance infinie. Dans cette configuration, en effet, l’effet d’occlusion induit par la vibration de la paroi du canal auditif uniquement est négligeable. La différence d’OE entre les bouchons d’oreille en mousse et en silicone a été attribuée au coefficient de Poisson du bouchon d’oreille (Carillo et al., 2021a). L’effet de Poisson correspond à l’expansion médiale et latérale du bouchon d’oreille en raison de sa compression radiale imposée par la vibration normale de la paroi du canal auditif. Cet effet est négligeable pour les bouchons d’oreille en mousse (ν=0.10) et plus important pour les bouchons d’oreille en silicone (ν=0.48). Par conséquent, un deuxième mécanisme de contribution a été mis en évidence pour expliquer la différence d’effet d’occlusion entre un bouchon d’oreille en mousse et un « bouchon d’oreille » à impédance infinie. Il s’agit de la vibration tangentielle de la paroi du canal auditif qui fait vibrer le bouchon d’oreille le long de l’axe du canal auditif (Carillo et al., 2021a). Grâce au modèle EF et à l’utilisation d’un modèle électroacoustique associé, les contributions importantes des bouchons d’oreille sur l’effet d’occlusion ont été pour la première fois expliquées.
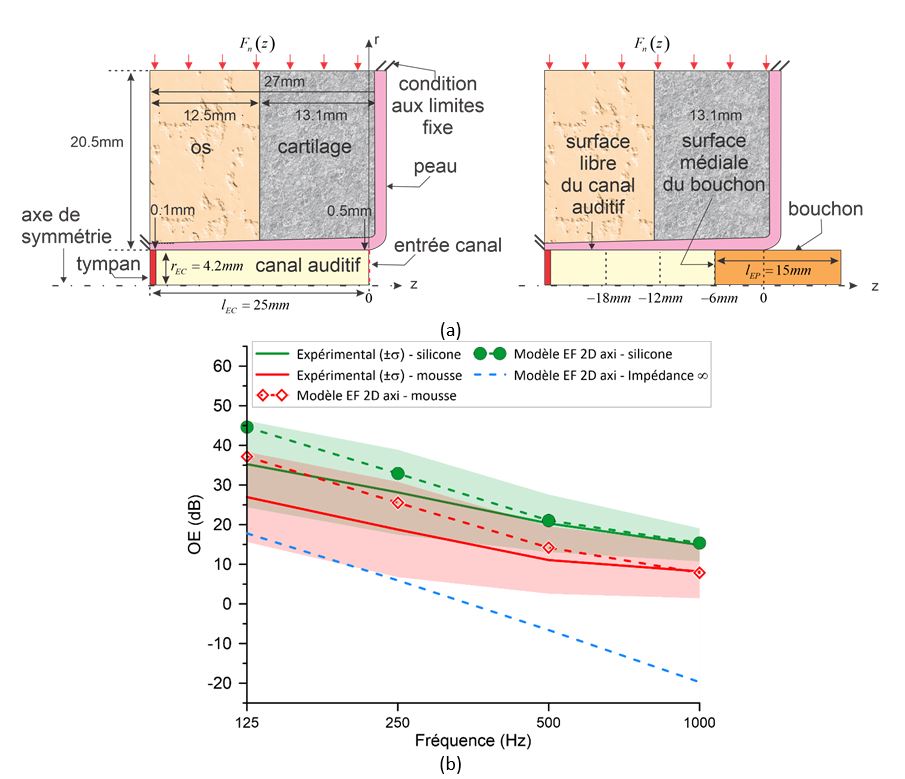
Références
Allard, J.-F. et Atalla, N. (2009). Propagation of sound in porous media: modelling sound absorbing materials (Second Edition). John Wiley and Sons.
Areias, B., Santos, C., Natal Jorge, R. M., Gentil, F. et Parente, M. P. (2016). Finite element modelling of sound transmission from outer to inner ear. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine, 230(11), 999‑1007. https://doi.org/10.1177/0954411916666109
Bathe, K.-J. (1996). Finite element procedures. Prentice Hall.
Benacchio, S., Doutres, ., Varoquaux, A., Wagnac, E., Le Troter, A., Callot, V. et Sgard, F. (2019). Use of magnetic resonance image registration to estimate displacement in the human earcanal due to the insertion of in-ear devices. The Journal of the Acoustical Society of America, 146(4), 2452‑2465. https://doi.org/10.1121/1.5126857
Benacchio, S., Doutres, O., Le Troter, A., Varoquaux, A., Wagnac, E., Callot, V. et Sgard, F. (2018). Estimation of the ear canal displacement field due to in-ear device insertion using a registration method on a human-like artificial ear. Hearing Research, 365, 16‑27. https://doi.org/10.1016/j.heares.2018.05.019
Benacchio, S., Doutres, O., Wagnac, E. et Sgard, F. (2020a, janvier). Design of realistic artificial ears dedicated to the study of the acoustic and physical comfort of in-ear hearing protectors (in french Conception d’oreilles artificielles réalistes dédiées à l’étude du confort acoustique et physique des protecteurs auditifs intra-auriculaires) (R-1106)[Research report, IRSST], 1-104.
Bériot, H. et Gabard, G. (2019). Anisotropic adaptivity of the p-FEM for time-harmonic acoustic wave propagation. Journal of Computational Physics, 378, 234‑256. https://doi.org/10.1016/j.jcp.2018.11.013
Bériot, H. et Modave, A. (2020). An automatic perfectly matched layer for acoustic finite element simulations in convex domains of general shape. International Journal for Numerical Methods in Engineering, nme.6560. https://doi.org/10.1002/nme.6560
Bériot, H., Prinn, A. et Gabard, G. (2016). Efficient implementation of high‐order finite elements for Helmholtz problems. International Journal for Numerical Methods in Engineering, 106(3), 213‑240. https://doi.org/10.1002/nme.5172
Boyer, S. (2015). Étude de la transmission sonore à travers un protecteur de type « coquilles » : modélisation numérique et validation expérimentale [Ph.D. thesis, École de technologie supérieure, Canada].
Boyer, S., Doutres, O., Sgard, F., Laville, F. et Boutin, J. (2015). Low Frequency Finite Element Models of the Acoustical Behavior of Earmuffs. The Journal of the Acoustical Society of America, 137(5), 2602‑2613.https://doi.org/10.1121/1.4919326
Brummund, M., Sgard, F., Petit, Y. et Laville, F. (2014a). Three-dimensional finite element modeling of the human external ear: Simulation study of the bone conduction occlusion effect. The Journal of the Acoustical Society of America, 135(3), 1433‑1444. https://doi.org/10.1121/1.4864484
Brummund, M. (2014b). Study of the occlusion effect induced by an earplug: numerical modelling and experimental validation [Ph.D. thesis, École de technologie supérieure, Canada].
Brummund, M., Sgard, F., Petit, Y., Laville, F. et Nélisse, H. (2015). An axisymmetric finite element model to study the earplug contribution to the bone conduction occlusion effect. Acta Acustica United with Acustica, 101(4), 775‑788. https://doi.org/10.3813/AAA.918872
Caminos, L., Torres, M. et Gonzalez-Herrera, A. (2015). Dynamic behavior of the human tympanic membrane using a viscoelastic model. Dans Proceedings of International Congress on Sound and Vibration, 1‑8.
Carillo, K., Doutres, O. et Sgard, F. (2020a). Theoretical investigation of the low frequency fundamental mechanism of the objective occlusion effect induced by bone-conducted stimulation. The Journal of the Acoustical Society of America, 147(5), 3476‑3489. https://doi.org/10.1121/10.0001237
Carillo, K., Doutres, O. et Sgard, F. (2020b). Theoretical investigation of the low frequency fundamental mechanism of the objective occlusion effect induced by bone-conducted stimulation. The Journal of the Acoustical Society of America, 147(5), 3476–3489. https://doi.org/10.1121/10.0001237
Carillo, K., Doutres, O. et Sgard, F. (2021a). Numerical investigation of the earplug contribution to the low frequency occlusion effect induced by bone-conducted stimulation. The Journal of the Acoustical Society of America, 150(3), 2006‑2023. https://doi.org/10.1121/10.0006209
Carillo, K., Sgard, F. et Doutres, O. (2018). Numerical study of the broadband vibro-acoustic response of an earmuff. Applied Acoustics, 134, 25‑33. https://doi.org/10.1016/j.apacoust.2017.12.025
Carillo, K., Sgard, F., Xu, H., Guilloteau, A., Benacchio, S., Poissenot-Arrigoni, B. et Doutres, O. (2021b). On the modeling of the objective occlusion effect induced by earplugs: Recent advances, challenges and perspectives. NHCA Spectrum, 38(2), 15‑22.
Champoux, Y. et Allard, J. (1991). Dynamic tortuosity and bulk modulus in air‐saturated porous media. Journal of Applied Physics, 70(4), 1975‑1979. https://doi.org/10.1063/1.349482
Chan, J. C. K. et Geisler, C. D. (1990). Estimation of eardrum acoustic pressure and of ear canal length from remote points in the canal. The Journal of the Acoustical Society of America, 87(3), 1237‑1247. https://doi.org/10.1121/1.398799
Chang, Y., Kim, N. et Stenfelt, S. (2016). The development of a whole-head human finite-element model for simulation of the transmission of bone-conducted sound. The Journal of the Acoustical Society of America, 140(3), 1635‑1651. https://doi.org/10.1121/1.4962443
Chang, Y. (2018). A Finite Element Model of the Human Head for Simulation of Bone-conducted Sound. [Ph.D. thesis, Linköping University, Sweden]. http://urn.kb.se/resolve?urn=urn:nbn:se:liu:diva-145666
Darkner, S. (2009). Shape and Deformation Analysis of the Human Ear Canal. [Ph.D. thesis, Technical University of Denmark, Denmark].
Darkner, S., Jønsson, S. et Sommer, S. (2017). In Vivo Study of the Human Ear Canal Using Contrast-Enhanced MRI.Dans Proceedings of ISMRM, 1-3. https://cds.ismrm.org/protected/17MProceedings/PDFfiles/4657.html
Darkner, S., Larsen, R. et Paulsen, R. R. (2007). Analysis of deformation of the human ear and canal caused by mandibular movement. Dans Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, 10, 801‑808.
Darkner, S., Sommer, S., Schuhmacher, A., Baandrup, H. I. A. O., Thomsen, C. et Jønsson, S. (2018). An Average of the Human Ear Canal: Recovering Acoustical Properties via Shape Analysis. arXiv:1811.03848 [cs]. https://arxiv.org/abs/1811.03848
De Greef, D., Pires, F. et Dirckx, J. J. J. (2017). Effects of model definitions and parameter values in finite element modeling of human middle ear mechanics. Hearing Research, 344, 195‑206. https://doi.org/10.1016/j.heares.2016.11.011
Delany, M. E. et Bazley, E. N. (1970). Acoustical properties of fibrous absorbent materials. Applied Acoustics, 3(2), 105‑116. https://doi.org/10.1016/0003-682X(70)90031-9
Gan, R.Z., Feng, B., and Sun, Q. (2004). Three-Dimensional Finite Element Modeling of Human Ear for Sound Transmission. Annals of Biomedical Engineering, 32, 847–859. https://doi.org/10.1023/b:abme.0000030260.22737.53
Gan, R. Z., Leckness, K., Smith, K. et Ji, X. D. (2019). Characterization of Protection Mechanisms to Blast Overpressure for Personal Hearing Protection Devices – Biomechanical Measurement and Computational Modeling. Military Medicine, 184(Supplement_1), 251‑260. https://doi.org/10.1093/milmed/usy299
Gan, R. Z., Reeves, B. P. et Wang, X. (2007). Modeling of Sound Transmission from Ear Canal to Cochlea. Annals of Biomedical Engineering, 35(12), 2180‑2195. https://doi.org/10.1007/s10439-007-9366-y
Gaudreau, M.-A., Sgard, F., Laville, F. et Nélisse, H. (2017). A finite element model to improve noise reduction based attenuation measurement of earmuffs in a directional sound field. Applied Acoustics, 119, 66‑77. https://doi.org/10.1016/j.apacoust.2016.12.003
Gilman, S. et Dirks, D. D. (1986). Acoustics of ear canal measurement of eardrum SPL in simulators. The Journal of the Acoustical Society of America, 80(3), 783‑793. https://doi.org/10.1121/1.393953
Hahn. K. S. (1985). The Effect of Variation in Ear Canal Skin Parameters on the Behavior of an Ear-Earplug Model. [Ph.D. thesis, University of Toronto, Canada].
Hudde, H. et Engel, A. (1998a). Measuring and modeling basic properties of the human middle ear and ear canal. Part I: Model structure and measuring techniques. Acustica – Acta Acustica, 84, 720‑738.
Hudde, H. et Engel, A. (1998c). Measuring and modeling basic properties of the human middle ear and ear canal. Part III: Eardrum impedances, transfer functions and model calculations. Acustica – Acta Acustica, 84, 1091‑1109.
James, C. (2006). Finite Element Modeling and Exploration of Double Hearing Protection Systems [Master thesis, Virginia Polytechnic Institute and State University].
Kampinga, W. R. (2010). Viscothermal acoustics using finite elements: analysis tools for engineers. [Ph.D. thesis, University of Twente, Netherlands] [Host. http://dx.doi.org/10.3990/1.9789036530507
Kampinga, W. R., Wijnant, Y. H. et de Boer, A. (2010). Performance of several viscothermal acoustic finite elements. Acta Acustica united with Acustica, 96(1), 115–124. http://dx.doi.org/10.3813/AAA.918262
Kersten, S., Sgard, F. et Vorlander, M. (2024). Impact of the ear canal motion on the impedance boundary conditions in models of the occlusion effect. The Journal of the Acoustical Society of America, 155(1), 56‑67. https://doi.org/10.1121/10.0024244
Kikidis, D., Bibas, A., Kikidis, D. et Bibas, A. (2014). A Clinically Oriented Introduction and Review on Finite Element Models of the Human Cochlea. BioMed Research International, 2014, 1‑8. https://doi.org/10.1155/2014/975070
Kim, N., Chang, Y. et Stenfelt, S. (2014). A Three-Dimensional Finite-Element Model of a Human Dry Skull for Bone-Conduction Hearing. BioMed Research International, 2014, 1‑9. https://doi.org/10.1155/2014/519429
Kinsler, L. E. et Frey, A. R. (2000). Fundamentals of Acoustics (4th éd.). Wiley & Sons.
Kringlebotn, M. (1988). Network model for the human middle ear. Scandinavian audiology, 17, 2, 75‑85. https://doi.org/10.3109/01050398809070695
Lafarge, D. et Lemarinier, P. (1997). Dynamic compressibility of air in porous structures at audible frequencies. The Journal of the Acoustical Society of America, 102, 1995‑2006. https://doi.org/10.1121/1.419690
Lee, C.-F., Chen, P.-R., Lee, W.-J., Chou, Y.-F., Chen, J.-H. et Liu, T.-C. (2010). Computer Aided Modeling of Human Mastoid Cavity Biomechanics Using Finite Element Analysis. EURASIP Journal on Advances in Signal Processing, 2010, 1‑10. https://doi.org/10.1155/2010/203037
Lee, D. et Ahn, T.-S. (2015). Statistical calibration of a finite element model for human middle ear. Journal of Mechanical Science and Technology, 29(7), 2803‑2815. https://doi.org/10.1007/s12206-015-0609-9
Luan, Y. (2021). Study of sound transmission through a double protectionsystem using the finite element method (in french « Étude de la transmission sonore à travers un système de double protection à l’aide de la méthode des éléments finis « ) [Ph.D., École de Technologie Supérieure, Canada].
Luan, Y., Doutres, O., Nelisse, H. et Sgard, F. (2021). Experimental study of earplug noise reduction in a double hearing protector on an acoustic test fixture. Applied Acoustics, 176, 1‑13. https://doi.org/10.1016/j.apacoust.2020.107856
Luan, Y., Sgard, F., Benacchio, S., Nélisse, H. et Doutres, O. (2019). A transfer matrix model of the IEC 60318-4 ear simulator: Application to the simulation of earplug insertion loss. Acta Acustica united with Acustica, 105(6), 1258‑1268. https://doi.org/10.3813/AAA.919403
Luan, Y., Sgard, F., Nélisse, H., and Doutres, O. (2022). A finite element model to predict the double hearing protector effect on an in-house acoustic test fixture. The Journal of the Acoustical Society of America, 151(3), 1860–1874. https://doi.org/10.1121/10.0009835
Miki, Y. (1990). Acoustical properties of porous materials-Generalizations of empirical models-. Journal of the Acoustical Society of Japan (E), 11(1), 25‑28. https://doi.org/10.1250/ast.11.25
Motallebzadeh, H., Maftoon, N., Pitaro, J., Funnell, W. R. J. et Daniel, S. J. (2016). Finite-Element Modelling of the Acoustic Input Admittance of the Newborn Ear Canal and Middle Ear. Journal of the Association for Research in Otolaryngology, 18(1), 25‑48. https://doi.org/10.1007/s10162-016-0587-3
Motallebzadeh, H., Maftoon, N., Pitaro, J., Funnell, W. R. J. et Daniel, S. J. (2017a). Finite-Element Modelling of the Acoustic Input Admittance of the Newborn Ear Canal and Middle Ear. Journal of the Association for Research in Otolaryngology, 18(1), 25‑48. https://doi.org/10.1007/s10162-016-0587-3
Motallebzadeh, H., Maftoon, N., Pitaro, J., Funnell, W. R. J. et Daniel, S. J. (2017b). Fluid-Structure Finite-Element Modelling and Clinical Measurement of the Wideband Acoustic Input Admittance of the Newborn Ear Canal and Middle Ear. Journal of the Association for Research in Otolaryngology, 18(5), 671‑686. https://doi.org/10.1007/s10162-017-0630-z
Nélisse, H., Le Cocq, C., Boutin, J., Laville, F. et Voix, J. (2015). Systematic evaluation of the relationship between physical and psychoacoustical measurements of hearing protectors’ attenuation. Journal of Occupational and Environmental Hygiene, 12, 829‑844. https://doi.org/10.1080/15459624.2015.1053893
Ni, G. (2012). Fluid coupling and waves in the cochlea [Ph.D. thesis, University of Southampton, United Kingdom].
Nie, X., Liu, H., Huang, X., Tan, J., Xie, X., Yao, W., Rao, Z. et Duan, M. (2011). Finite element model of human ear reconstruction through micro-computer tomography. Acta Oto-laryngologica, 131(3), 269‑276. https://doi.org/10.3109/00016489.2010.542487
Olny, X. (1999). Absorption acoustique des milieux poreux à simple et double porosité. Modélisation et validation expérimentale [PhD. thesis, INSA de Lyon, France].
Pierce, A. D. (1994). Acoustics: an introduction to its physical principles and applications. Published by the Acoustical Society of America through the American Institute of Physics.
Poissenot-Arrigoni, B., Benacchio, S., Doutres, O. et Sgard, F. (2019). An artificial ear to assess objective indicators related to the acoustical comfort dimension of earplugs: validation of a vibro acoustic model for insertion loss and occlusion effect assessment. Dans Proceedings of International Congress on Sound and Vibration, 1‑8.
Reinfeldt, S., Stenfelt, S. et Håkansson, B. (2013). Estimation of bone conduction skull transmission by hearing thresholds and ear-canal sound pressure. Hearing Research, 299, 19–28. https://doi.org/10.1016/j.heares.2013.01.023
Schmidt, S. et Hudde, H. (2009). Accuracy of acoustic ear canal impedances: Finite element simulation of measurement methods using a coupling tube. The Journal of the Acoustical Society of America, 125(6), 3819‑3827. https://doi.org/10.1121/1.3125344
Schroeter, J. et Poesselt, C. (1986). The use of acoustical test fixtures for the measurement of hearing protector attenuation. Part II : Modeling the external ear, simulating bone conduction, and comparing test fixture and real-ear data. The Journal of the Acoustical Society of America, 80(2), 505‑527. https://doi.org/10.1121/1.394046
Sgard, F., Carillo, K. et Doutres, O. (2019). A 2D axisymmetric finite element model to assess the contribution of in-ear hearing protection devices to the objective occlusion effect. Dans Proceedings of Internoise, 259, 2494-2505.
Sgard, F., Nélisse, H., Gaudreau, M.-A., Boutin, J., Voix, J. et Laville, F. (2010b). Étude de la transmission sonore à travers les protecteurs auditifs et application d’une méthode pour évaluer leur efficacité effective en milieu de travail – Partie 2 : Étude préliminaire d’une modélisation des protecteurs auditifs par éléments finis (R-680). [Research report, IRSST], 1-100.
Sgard, F., Nélisse, H., Laville, F., Petit, Y., Boutin, J., Le Cocq, C., Brummund, M., Boyer, S., Viallet, G., Doutres, O., Gaudreau, M.-A., Voix, J. (2016). Développement d’outils et de méthodes pour mieux évaluer et améliorer la protection auditive individuelle des travailleurs (R-901). [Research report, IRSST], 1–132.
Shaw, E. A. G. et Stinson, M. R. (1981). Network concepts and energy flow in the human middle ear. J. Acoust. Soc. Am., 69(1), 43.
Stenfelt, S. et Goode, R. L. (2005). Bone-conducted sound: physiological and clinical aspects. Otology & Neurotology: Official Publication of the American Otological Society, American Neurotology Society [and] European Academy of Otology and Neurotology, 26(6), 1245‑1261. https://doi.org/10.1097/01.mao.0000187236.10842.d5
Stenfelt, S., Hato, N. et Goode, R. L. (2002). Factors contributing to bone conduction: The middle ear. J. Acoust. Soc. Am., 111(2), 947‑959. https://doi.org/10.1121/1.1432977
Stenfelt, S., Wild, T., Hato, N. et Goode, R. L. (2003). Factors contributing to bone conduction: the outer ear. J. Acoust. Soc. Am., 113(2), 902‑913. https://doi.org/10.1121/1.1534606
Stinson, M. R. et Lawton, B. W. (1989). Specification of the geometry of the human ear canal for the prediction of sound‐pressure level distribution. The Journal of the Acoustical Society of America, 85(6), 2492‑2503. https://doi.org/10.1121/1.397744
Stirnemann, A. (2011). A. Stirnemann: Ein Mittelohrmodell basierend auf 692 der Aussenohr-Transferimpedanz. Dans Proceedings of DAGA, 1-2.
Sun, Q., Gan, R. Z., Chang, K.-H. et Dormer, K. J. (2002). Computer-integrated finite element modeling of human middle ear. Biomechanics and Modeling in Mechanobiology, 1, 109‑122. https://doi.org/10.1007/s10237-002-0014-z
Suzuki, S., Maruyama, S. et Ido, H. (1989). Boundary element analysis of cavity noise problems with complicated boundary conditions. Journal of Sound and Vibration, 130(1), 79‑96. https://doi.org/10.1016/0022-460X(89)90521-X
Tian, J., Zhang, J., Rao, Z., Ta, N. et Xu, L. (2015). Numerical analysis of middle ear pressure effects on performance of implantable hearing devices. Dans Proceedings of International Congress on Sound and Vibration, 1‑8.
Viallet, G., Sgard, F., Laville, F. et Boutin, J. (2013). Axisymmetric versus three-dimensional finite element models for predicting the attenuation of earplugs in rigid walled ear canals. J. Acoust. Soc. Am., 134(6), 4470‑4480. https://doi.org/10.1121/1.4826182
Viallet, G., Sgard, F., Laville, F. et Boutin, J. (2014). A finite element model to predict the sound attenuation of earplugs in an acoustical test fixture. The Journal of the Acoustical Society of America, 136(3), 1269‑1280. http://dx.doi.org/10.1121/1.4890645
Viallet, G., Sgard, F., Laville, F. et Nélisse, H. (2015). Investigation of the variability in earplugs sound attenuation measurements using a finite element model. Applied Acoustics, 89, 333‑344. https://doi.org/10.1016/j.apacoust.2014.10.007
Volandri, G., Carmignani, C., Di Puccio, F. et Forte, P. (2014). Finite Element Formulations Applied to Outer Ear Modeling. Journal of Mechanical Engineering, 60(5), 363‑372. https://doi.org/10.5545/sv-jme.2014.1837
Volandri, G., Di Puccio, F., Forte, P. et Manetti, S. (2012). Model-oriented review and multi-body simulation of the ossicular chain of the human middle ear. Medical Engineering & Physics, 34(9), 1339‑1355. https://doi.org/10.1016/j.medengphy.2012.02.011
Walsh, T., Demkowicz, L. et Charles, R. (2004). Boundary element modeling of the external human auditory system. The Journal of the Acoustical Society of America, 115(3), 1033‑1043. https://doi.org/10.1121/1.1643360
Wang, X., Wang, L., Zhou, J. et Hu, Y. (2014). Finite element modelling of human auditory periphery including a feed-forward amplification of the cochlea. Computer Methods in Biomechanics and Biomedical Engineering, 17(10), 1096‑1107. https://doi.org/10.1080/10255842.2012.737458
Wang, H., Merchant, S.N., and Sorensen, M.S. (2007). A Downloadable Three-Dimensional Virtual Model of the Visible Ear. ORL, 69, 63–67. https://doi.org/10.1159/000097369
Xu, H. (2022). Prediction of vibroacoustic behavior of a human head wearing earplugs by a finite element method [Ph.D., École de Technologie Supérieure, Canada].
Xu, H., Sgard, F., Carillo, K., Wagnac, E., and De Guise, J. (2021). Simulation of the objective occlusion effect induced by bone-conducted stimulation using a three-dimensional finite-element model of a human head. The Journal of the Acoustical Society of America, 150(5), 4018–4030. https://doi.org/10.1121/10.0007230
- On fait principalement référence ici aux matériaux poreux à cellules ouvertes comme les inserts en mousse placés dans les serre-têtes ou les coussins des serre-têtes. Dans la littérature portant sur la modélisation des protecteurs auditifs, ces matériaux sont essentiellement décrits par des modèles de fluide équivalents à squelette rigide ou souple (voir (Allard et Atalla, 2009) à ce propos) du fait de leurs conditions aux limites au sein du serre-tête. Un modèle de Biot faisant intervenir les pores de la phase fluide et un champ de déplacement de la phase solide pourrait éventuellement être utilisé mais cela n’est pas abordé dans ce chapitre. Notons que les matériaux poreux constituant les bouchons sont considérés comme des matériaux viscoélastiques du fait que les pores en surface sont fermés par une membrane. ↵
- Pour ce genre de problèmes où l’on s’intéresse à la pression au centre du canal, un modèle analytique est tout-à-fait suffisant. ↵
- En pratique, les bouchons sur mesure sont faits légèrement plus grands que le canal auditif afin d’assurer une bonne étanchéité tout en n’induisant pas d’inconfort mécanique. Le canal auditif est donc déformé. ↵
- On pourrait ajouter le fluide cochléaire mais pour la problématique qui nous intéresse ici, ce fluide n’est pas modélisé. La cochlée peut en effet être remplacée par une impédance mécanique appliquée sur la platine de l’étrier. ↵
- Des non linéarités géométriques peuvent apparaitre pour des niveaux sonores très élevés. ↵
- Une fuite peut être considérée comme un orifice rempli d’air dont la section droite est de dimension très faible par rapport à la longueur d’onde et qui traverse le protecteur. Dans cet orifice, les effets viscothermiques ne peuvent être ignorés. ↵
- Au contraire des autres modèles mentionnés qui font intervenir la pression acoustique seule, le fluide est ici décrit par plusieurs variables : le vecteur vitesse particulaire, la température acoustique et la pression acoustique. ↵
- Il s’agit de la pression acoustique totale. Dans le cas d’une sollicitation acoustique, elle résulte de l’onde acoustique incidente et de l’onde acoustique rayonnée par les tissus du canal et la membrane tympanique. Dans le cas d’une sollicitation purement solidienne, elle résulte de l’onde acoustique rayonnée par les tissus du canal et la membrane tympanique. ↵
- Un comportement à réaction localisée est associé à celui d’un matériau constitué de pores droits non connectés si bien que la pression acoustique en un point de la surface induit une réaction seulement en ce point. En d’autres termes, ce qui se passe en un point ne dépend que de la position de ce point et pas du reste de la surface. La conséquence est que l’impédance acoustique de surface est indépendante du champ de pression incident. ↵
- Tout se passe comme s’il n’y avait qu’un seul fluide qui occupe l’espace extérieur et le canal auditif. ↵
- i.e en tout point de l’interface il y a continuité des déplacements et tractions entre les deux solides. ↵
- Dans le cas des serre-têtes, l’effet acoustique de l’arceau peut être intégré dans le calcul. L’arceau peut être considéré comme un solide élastique mais dans la littérature existante, est simplement pris en compte comme un objet rigide acoustique. Il est donc supposé influencer le champ acoustique autour de la tête et du protecteur par son effet de diffraction acoustique s’il ne bougeait pas. ↵
- Notons qu’il est possible de prendre en compte la présence d’adhésif entre contre-plaque et coussin à travers une couche très mince de matériau viscoélastique. Par exemple, Carillo a étudié l’effet de la présence d’adhésif entre la contreplaque et un coussin en plomb fabriqué pour l’occasion, sur la perte par insertion de la coque de l’EAR-1000 couplée à ce coussin (Carillo et al., 2018). ↵
- [latex]\phi_{inc}[/latex] appelé longitude est l'angle formé par l’axe [latex]\underline e_1[/latex] et la projection orthogonale de [latex]\underline k_{inc}[/latex] dans le plan [latex](O,x_1,x_2)[/latex]. [latex]\theta_{inc}[/latex] appelé colatitude (ou angle zénithal) est l'angle non orienté formé par les vecteurs [latex]\underline e_3[/latex] et [latex]\underline k_{inc}[/latex]. ↵
- Pour des éléments finis classiques (interpolation de type « h ») 4 éléments par longueur d’onde lorsque des éléments quadratiques sont utilisés et 6 pour des éléments linéaires. Pour les milieux poroélastiques, ce nombre d’éléments peut être beaucoup plus élevé. ↵
- [latex]{c_s} = \sqrt {\frac{{{E_s}}}{{2{\rho _s}\left( {1 + {\nu _s}} \right)}}}[/latex] ↵
- [latex]{c_p} = \sqrt {\frac{{{E_s}\left( {1 - {\nu _s}} \right)}}{{{\rho _s}\left( {1 + {\nu _s}} \right)\left( {1 - 2{\nu _s}} \right)}}}[/latex] avec [latex]E_s[/latex], [latex]\nu_s[/latex] le module d’Young et le coefficient de Poisson. ↵
- Les méthodes directes calculent la solution du problème en effectuant des opérations matricielles de type factorisation. Ce sont des variantes de l’élimination Gaussienne. Dans les méthodes itératives, on cherche à minimiser la norme du résidu en partant d’une estimation de la solution. La solution est ajustée au fil des itérations en fonction de la valeur du résidu et d’autres quantités qui dépendent de l’algorithme considéré jusqu’à ce que le résidu soit en-dessous d’une tolérance spécifiée. ↵
- Ces solveurs diffèrent principalement par leur vitesse. Par exemple PARDISO tend à être le plus rapide et SPOOLES le plus lent mais SPOOLES utilise moins de mémoire. Certains solveurs comme MPUMPS et PARDISO peuvent stocker la solution sur le disque plutôt qu’en mémoire vive, ce qui permet de résoudre des problèmes de grande taille même avec une mémoire vive limitée. ↵
- Voir https://doc.comsol.com/6.2/docserver/#!/com.comsol.help.comsol/comsol_ref_solver.34.136.html et https://www.mathworks.com/help/matlab/math/iterative-methods-for-linear-systems.html ↵
Éléments finis
Imagerie par résonance magnétique
Couche parfaitement adaptée (Perfectly Matched Layer)
Perte par insertion (Insertion Loss) [dB]
Montage d’essai acoustique (Artificial test fixture)
Affaiblissement sonore (Noise Reduction) [dB]
Effet d’occlusion (occlusion effect) [dB]
Microphone-In-Real-Ear
Effet d’occlusion (occlusion effect) [dB]

