Circuits combinatoires typiques

Guy Bégin

6 Circuits combinatoires typiques

1.1. Objectifs

Analyser un circuit combinatoire à partir de son schéma
Concevoir un circuit combinatoire à partir d’une spécification
Connaître différentes approches de réalisation
Se familiariser avec les principaux circuits combinatoires courants et leurs fonctions : additionneur, décodeur, multiplexeur, encodeur, comparateur
Comprendre le fonctionnement d’une chaîne d’addition binaire et les mécanismes de propagation et d’anticipation de retenue

1.2. Circuit combinatoire

Un circuit logique combinatoire est une combinaison de portes logiques dont la sortie à un instant donné ne dépend que des valeurs des entrées à cet instant. Un circuit combinatoire à $n$ entrées et $m$ sorties peut être représenté par un schéma-bloc, dans lequel on place généralement les entrées à gauche et les sorties à droite.

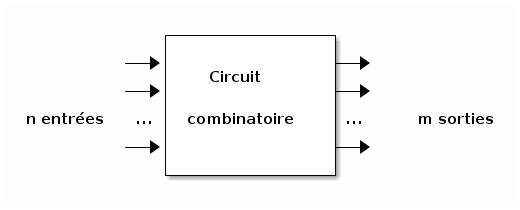
Circuit combinatoire à n entrées et m sorties.

Figure 1 : Circuit combinatoire

Avec $n$ entrées, il est possible de créer $2^n$ combinaisons différentes des entrées binaires. Pour chaque combinaison, le circuit peut donner une sortie 0 ou 1. On peut donc préciser la fonction réalisée par le circuit au moyen d’un tableau de vérité comportant $2^n$ lignes. Comme nous avons $m$ sorties différentes, il y aura $m$ colonnes dans le tableau de vérité pour les fonctions de sortie. Traditionnellement, on présente les entrées en ordre croissant de combinaisons binaires.

1.3. Analyse d’un circuit logique combinatoire

Si on se trouve devant le schéma d’un circuit logique dont on ne connaît pas la fonction, on doit en faire l’analyse. La première étape consiste à vérifier qu’il s’agit bien d’un circuit combinatoire. Si le schéma ne comporte pas de cellules de mémoire ou de boucles de rétroaction, on peut conclure que le circuit est combinatoire. Une boucle de rétroaction consiste en un chemin du circuit par lequel une valeur d’entrée d’une porte provient, directement ou indirectement (par l’intermédiaire d’autres portes), de la sortie de la même porte. La présence de rétroaction est une caractéristique des circuits logiques séquentiels, que nous étudierons plus loin.

Pour interpréter le comportement du circuit, nous devons déterminer les expressions logiques qu’il met en oeuvre ou établir son tableau de vérité.

Pour déterminer l’expression logique, on procède ainsi :

Étiqueter toutes les sorties des portes qui sont alimentées par les variables d’entrée du système. Les noms de variables seront arbitraires, mais devraient être choisis de façon à faciliter l’interprétation par la suite. Déterminer les fonctions logiques pour ces variables.
Étiqueter les sorties des portes qui sont alimentées par les variables d’entrée et par les sorties étiquetées à l’étape précédente. Déterminer les fonctions logiques pour ces nouvelles variables.
Répéter l’étape 2 jusqu’à arriver aux variables de sortie du système.
En substituant les expressions logiques des fonctions identifiées, déterminer l’expression logique pour les sorties du système en fonction des entrées du système.

1.3.1. Exemple

Analysons le circuit combinatoire illustré à la figure suivante.

Circuit combinatoire à analyser.

Figure 2 : Circuit combinatoire à analyser

Il n’est pas la peine d’étiqueter la sortie de la porte inverseur. Comme variables intermédiaire, on considère 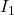$I_1$ en sortie de la porte ET à trois entrées et 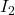$I_2$ en sortie de la porte NOR. On trouve que 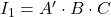$I_1 = A^\prime \cdot B \cdot C$ et que $I_2 = (A + D)^\prime = A^\prime \cdot D^\prime$ .
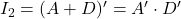On aura donc $F_1 = I_1 \cdot I_2$ .
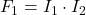En substituant, $F_1 = ( A^\prime \cdot B \cdot C ) \cdot ( A^\prime \cdot D^\prime) = A^\prime \cdot B \cdot C \cdot D^\prime$ .
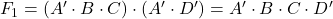En simplifiant, on obtient finalement $F_1 = A^\prime \cdot B \cdot C \cdot D^\prime$ .

Tableau 1 : Tableaux de vérité des fonctions intermédiaires et de la sortie
$A$	$C$	$B$	$D$	$I_1$	$I_2$	$F_1$
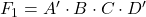0	0	0	0	0	0	0
0	0	0	1	0	0	0
0	1	0	0	0	1	0
0	1	0	1	0	0	0
0	0	1	0	0	1	0
0	0	1	1	0	0	0
0	1	1	0	1	1	1
0	1	1	1	1	0	0
1	0	0	0	0	0	0
1	0	0	1	0	0	0
1	1	0	0	0	0	0
1	1	0	1	0	0	0
1	0	1	0	0	0	0
1	0	1	1	0	0	0
1	1	1	0	0	0	0
1	1	1	1	0	0	0

1.4. Conception d’un circuit combinatoire

Concevoir un circuit logique commence avec la formulation de la ou des fonctions du système et se termine avec une implémentation en portes logiques des fonctions logiques correspondantes. Voici les étapes à suivre.

À partir de l’expression du besoin ou des spécifications du système, déterminer combien d’entrées et de sorties sont requises, et puis leur assigner des noms de variables. Le choix des noms devrait faciliter leur interprétation en lien avec leur fonction.
Formuler le tableau de vérité qui décrit les valeurs logiques que doivent assumer les sorties en fonction des différentes combinaisons d’entrées.
Simplifier les expressions logiques pour les différentes fonctions, en tenant éventuellement compte des partages possibles d’éléments intermédiaires.
Tracer le circuit logique résultant et le valider (à la main ou mieux, par simulation).

L’étape 2 est cruciale, car ce qui sera implémenté (s’il n’y a pas d’erreurs) est exactement ce que le tableau de vérité stipule. On doit donc s’assurer que le tableau est correctement rempli et représente véritablement les besoins identifiés. Si des hypothèses ou des choix doivent être faits, notamment dans le cas où l’expression informelle des besoins est incomplète ou ambiguë, ces choix doivent être clairement identifiés et documentés, permettant le cas échéant de les modifier lorsque le système est mis à l’épreuve en fonctionnement.

N’importe quelle méthode de simplification peut être utilisée pour l’étape 3, mais il faut aussi prendre en compte le type de portes disponibles pour l’implémentation, les délais de propagations à travers les portes, le nombre d’interconnexions entre sorties et entrées de portes, et tout autre facteur pratique susceptible d’orienter les décisions.

1.5. Alternatives d’implémentation

Considérons la fonction logique $Y$ correspondant au diag-K de la figure suivante.

Diag-K d'une fonction combinatoire Y à réaliser.

Figure 3 : Diag-K d’une fonction combinatoire $Y$ à réaliser

1.5.1. Implémentations via la fonction directe

Implémentation en somme de produits

En somme de produits, on a 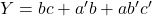$Y = bc + a^\prime b + a b^\prime c^\prime$ pour la fonction et 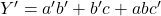$Y^\prime = a^\prime b^\prime + b^\prime c + a b c^\prime$ pour son complément. Les implémentations possibles pour la fonction directe sont illustrées ci-dessous.

Figure 4 : Implémentation de 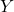$Y$ en somme de produits

Figure 5 : Implémentation (en NAND) de 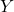$Y$ en somme de produits
Implémentation en produit de sommes

En produit de sommes, on a 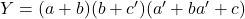$Y =(a + b ) (b + c^\prime ) (a^\prime + ba^\prime + c)$ pour la fonction et 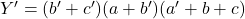$Y^\prime = (b^\prime +c^\prime )(a+b^\prime )(a^\prime +b+c)$ pour son complément. Les implémentations possibles pour la fonction directe sont illustrées ci-dessous.

Figure 6 : Implémentation de 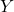$Y$ en produit de sommes

Figure 7 : Implémentation (en NOR) de 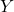$Y$ en produit de sommes

1.5.2. Implémentations via la fonction complémentaire

On peut aussi implémenter la fonction à partir de la fonction complémentaire $Y^\prime$ , en se basant sur le complément $Y^\prime = (b^\prime +c^\prime )(a+b^\prime )(a^\prime +b+c)$ et en inversant la sortie. Voici les implémentations que l’on obtient alors.

Implémentation en somme de produits

En somme de produits, on a utilisé une porte NOR en sortie pour obtenir finalement $Y$ .

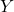Figure 8 : Implémentation via 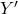$Y^\prime$ en somme de produits

Une autre forme fait appel à des portes NAND au premier niveau.

Figure 9 : Implémentation via 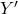$Y^\prime$ en somme de produits
Implémentation en produit de sommes

En produit de sommes, en se basant sur le complément 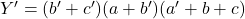$Y^\prime = (b^\prime +c^\prime )(a+b^\prime )(a^\prime +b+c)$ . On a encore ici deux variantes selon le type de portes utilisées.

Figure 10 : Implémentation via 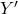$Y^\prime$ en produit de sommes

Figure 11 : Implémentation via 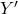$Y^\prime$ en produit de sommes

1.6. Circuits logiques combinatoires classiques

Nous allons maintenant nous intéresser à un certain nombre de fonctions typiques que l’on rencontre fréquemment en circuits logiques. Ce sera aussi l’occasion de mettre en pratique les approches de conception que nous avons vues.

1.7. Additionneur binaire

Une des opérations binaires les plus utilisées est l’addition (et la soustraction). Nous avons présenté à la section Addition de nombre non signés le tableau de vérité pour un additionneur binaire dont les entrées sont $a_{i}$ et $b_{i}$ , les bits des nombres à additionner, et aussi $r_{i-1}$ , la retenue provenant de la position $i-1$ . En sortie, on aura la somme $S_{i}$ et la retenue $R_{i}$ . Notez que pour bien distinguer la retenue d’entrée de la retenue de sortie, nous utilisons un symbole minuscule, $r_{i-1}$ , pour l’entrée et un symbole majuscule, $R_{i}$ , pour la sortie.

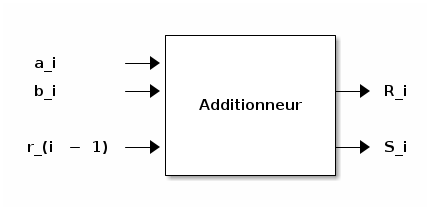
Schéma-bloc d'un additionneur complet.

Figure 12 : Schéma-bloc d’un additionneur complet

Tableau 2 : Tableau de vérité pour l’additionneur binaire
$a_{i}$	$b_{i}$	$r_{i-1}$	$R_{i}$	$S_{i}$
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

1.7.1. Demi-additionneur

Un circuit logique qui effectue l’addition de deux bits est appelé un demi-additionneur. Mais ce qu’il nous faut vraiment, c’est un additionneur complet, c’est-à-dire un circuit de trois entrées qui fait l’addition de trois bits, puisqu’il faudra pouvoir tenir compte de la retenue du niveau précédent pour effectuer l’addition sur un niveau. Il est possible d’implémenter l’additionneur complet avec deux demi-additionneurs.

Tableau 3 : Tableau de vérité pour un demi-additionneur
$a_{i}$	$b_{i}$	$R_{i}$	$S_{i}$
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

À partir du tableau de vérité, on peut trouver que pour un demi-additionneur, $S_{i} = a_i b_i^\prime + a_i^\prime b_i = a_i \operatorname{Xor} b_i$ et $R_{i} = a_i b_i$ .

Circuit demi-additionneur (en S de P).

Figure 13 : Circuit demi-additionneur (en S de P)

Circuit demi-additionneur avec porte XOR.

Figure 14 : Circuit demi-additionneur avec porte XOR

1.7.2. Additionneur complet

Une addition binaire complète de deux arguments constitués de $n$ bits procède du bit le moins significatif vers le bit le plus significatif, en additionnant à chaque étape trois bits : $a_{i}$ , $b_{i}$ et $r_{i-1}$ et en produisant une somme $S_{i}$ et une retenue $R_{i}$ .

Diag-K pour S_i.

Figure 15 : Diag-K pour $S_i$ , additionneur complet

Diag-K pour R_i.

Figure 16 : Diag-K pour $R_i$ , additionneur complet

Les expressions simplifiées sont

$S_{i} = a_i^\prime b_i^\prime r_{i-1} + a_i^\prime b_i r_{i-1}^\prime + a_i b_i^\prime r_{i-1}^\prime + a_i b_i r_{i-1}$

$R_{i} = a_i b_i + a_i r_{i-1} + b_i r_{i-1}$

Circuit pour S_i.

Figure 17 : Circuit additionneur complet pour $S_i$

Circuit pour R_i.

Figure 18 : Circuit additionneur complet pour $R_i$

Comme nous le disions précédemment, il est possible de combiner deux demi-additionneurs pour réaliser un additionneur complet, comme on peut le voir ici.

Circuit additionneur complet comportant deux demi-additionneurs et une porte OU.

Figure 19 : Circuit additionneur complet comportant deux demi-additionneurs et une porte OU

1.7.3. Additionneur binaire pour 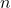$n$ bits

Un additionneur binaire est un circuit logique qui permet d’évaluer la somme arithmétique de deux nombres binaire de $n$ bits. Il peut être conçu en combinant des additionneurs complets en cascade, en reliant la retenue de sortie provenant de la position 0 (la moins significative) à l’entrée de retenue de la position 1, la retenue de sortie provenant de la position 1 à l’entrée de retenue de la position 2, …, la retenue de sortie provenant de la position $i-1$ à l’entrée de retenue de la position $i$ , etc. (figure 20).

Pour en faire un circuit général pouvant également se combiner en chaîne, on prévoit une entrée pour une retenue au niveau 0, $r_0$ et une sortie pour une retenue du dernier niveau $n-1$ , $R_{n-1}$ . On doit donc, pour le chaînage, acheminer la sortie retenue du niveau courant à l’entrée de retenue du niveau suivant.

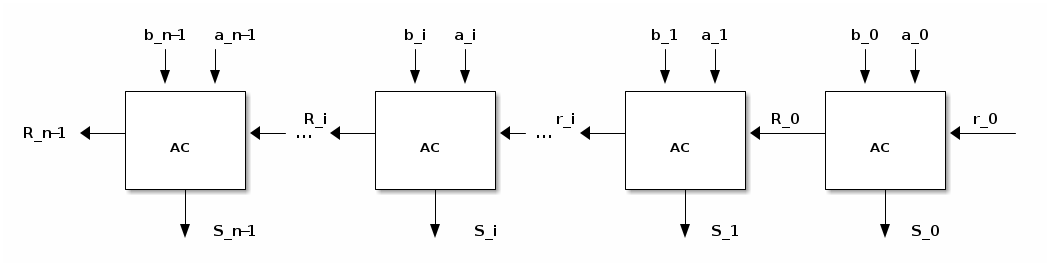
Chaîne d'addition pour n bits

Figure 20 : Chaîne d’addition

Cette réalisation en forme de chaîne, en réutilisant de façon systématique un bloc élémentaire, est avantageuse du point de vue de la complexité et de la flexibilité. Imaginons par exemple le défi de concevoir un additionneur binaire pour des nombres de quatre bits avec la méthode classique. Comme il faudrait considérer 9 entrées, le tableau de vérité comporterait $2^9= 512$ lignes!

1.7.4. Propagation de retenue

L’approche en cascade ne comporte pas que des avantages. Lorsqu’on effectue l’addition de deux nombres, les bits d’entrée des deux arguments et la retenue d’entrée sont présentés en même temps à l’additionneur. Comme dans tout circuit combinatoire, il faut un certain délai avant que les sorties n’atteignent leur niveau de sortie final. Ce délai de propagation dépend de la profondeur du circuit, en nombre de portes élémentaires à franchir de l’entrée vers la sortie. Et c’est évidemment le chemin le plus long qui détermine le délai de propagation global.

Dans le cas de l’additionneur, le chemin de propagation le plus long est celui qui mène à la dernière retenue finale $R_{n-1}$ . En effet, pour pouvoir calculer $R_{n-1}$ , bien que les valeurs de $a_{n-1}$ et $b_{n-1}$ soient déjà disponibles, il faut attendre que la valeur de $r_{n-1} = R_{n-2}$ soit stabilisée avant que le calcul puisse s’effectuer avec les bonnes valeurs. Il en est de même avec le bloc précédent, et ainsi, en remontant la chaîne vers $r_0$ , on trouve le chemin de propagation de retenue comme chemin le plus long.

Pour déterminer le nombre de portes à franchir pour le chemin de propagation de retenue, nous avons ajouté deux sorties intermédiaires à notre circuit d’additionneur complet, $P_i$ et $G_i$ , permettant de récrire la sortie comme $S_i = P_i \operatorname{Xor} r_i$ et la retenue de sortie comme $R_i = P_i r_i + G_i$ . Les signaux $P_i$ et $G_i$ ne dépendent que des entrées et sont donc disponibles après le délai des portes ET et XOR. Le chemin de $r_i$ à $R_i$ passe par une porte ET et une porte OU. Pour un additionneur de $n$ bits comprenant $n$ additionneurs complets, on aura une profondeur de retenue totale de $2n$ portes.

Circuit additionneur complet montrant les signaux intermédiaires de propagation, P_i et et de génération, G_i

Figure 21 : Circuit additionneur complet montrant les signaux intermédiaires $P_i$ et $G_i$

1.7.5. Anticipation de retenue

Les valeurs calculées par le circuit complet en chaîne ne seront valides et ne devront être prises en compte que lorsque le délai maximal se sera écoulé. Entre-temps, les valeurs binaires présentes aux différentes sorties assumeront typiquement des valeurs changeantes jusqu’à la stabilisation finale. Le délai de propagation de retenue est un facteur qui limite la vitesse à laquelle on pourra calculer la somme de deux nombres. Et comme l’addition est une opération souvent utilisée, parfois à répétition, pour réaliser d’autres opérations arithmétiques, cette limitation est problématique.

Il serait en théorie possible de ramener à un minimum le délai de calcul de la retenue finale en réalisant cette fonction en deux niveaux, par exemple avec un produit de sommes. Cette option n’est pas réaliste, car le nombre d’entrées à considérer en parallèle est prohibitif.

Comme solutions de compromis intermédiaires, un certain nombre de mécanismes ont été élaborés, dont l’approche par anticipation de retenue, que nous allons explorer ici. On fait appel aux deux signaux $P_i = a_i \operatorname{Xor} b_i$ et $G_i = a_i b_i$ , qui donnent respectivement pour la sortie et la retenue de sortie

$S_i = P_i \operatorname{Xor} r_{i-1}$

$R_i = P_i r_{i-1} + G_i$

$G_i$ est le signal qui indique la génération de retenue, produisant une retenue lorsque $a_i$ et $b_i$ sont tous deux à 1, sans égard à la valeur de la retenue d’entrée $r_{i-1}$ . Le signal $P_i$ est l’indicateur de propagation de retenue, parce qu’il détermine si la retenue du niveau précédent $r_{i-1}$ sera propagée à $R_i$ .

En partant du niveau 0, voici les expressions pour les différentes retenues :

$R_0 = r_0 = \operatorname{in}$

$R_1 = G_0 + P_0 R_0$

$R_2 = G_1 + P_1 R_1 = G_1 + P_1 (G_0 + P_0 R_0) = G_1 + P_1 G_0 + P_1 P_0 R_0$

$R_3 = G_2 + P_2 R_2 = G_2 + P_2 G_1 + P_2 P_1 G_0 + P_2 P_1 P_0 R_0$

etc.

Les expressions pour les retenues successives sont en forme somme de produits, ce qui mène à une implémentation à deux niveaux pour calculer les retenues rapidement. Contrairement à l’approche de propagation de retenue, toutes les retenues sont obtenues après un même délai équivalent à une profondeur de deux portes. En calculant d’abord les différentes valeurs de $P_i$ et $G_i$ pour chaque niveau et en utilisant ces résultats intermédiaires pour, d’une part, alimenter le circuit d’anticipateur de retenue et, d’autre part, effectuer $S_i = P_i \operatorname{Xor} r_i$ , on obtient un additionneur parallèle plus rapide que la configuration en cascade.

Circuit d'anticipateur de retenue pour n= 4.

Figure 22 : Circuit d’anticipateur de retenue pour $n= 4$

1.7.6. Soustraction

Pour effectuer une soustraction $A - B$ , il faut effectuer $A + (-B)$ , c’est-à-dire additionner le complément à deux de $B$ à $A$ . On détermine le complément à deux en obtenant d’abord le complément à un en complémentant chaque bit et en additionnant ensuite 1 à cette valeur par le biais de l’entrée de retenue de l’additionneur. Il est ainsi possible de concevoir un additionneur/soustracteur commandé par un signal de contrôle $O$ . Si $O=0$ , le circuit calcule $A + (B)$ et si $O=1$ , le circuit calcule $A + (-B)$ .

La complémentation de $B$ se fait au moyen de portes XOR qui calculent $O \operatorname{Xor} b_i$ et dont la sortie est acheminée à l’entrée $B$ de l’additionneur. Lorsque que l’entrée $O=1$ , leur sortie vaut $b_i^\prime$ .

Circuit additionneur/soustracteur 4 bits.

Figure 23 : Circuit additionneur/ soustracteur 4 bits

1.7.7. Débordements

Un additionneur ou un soustracteur est conçu en fonction d’une taille de nombres $n$ . Lorsque le résultat de l’opération dépasse la limite pouvant être représentée, on doit détecter cette condition et la signaler par un signal binaire.

Le cas de l’addition de nombres non signés est le plus simple. Il suffit de surveiller la retenue du niveau le plus significatif. Une retenue de 1 signifie un débordement de l’addition.

Les calculs avec des nombres signés en complément à deux peuvent aussi occasionner des débordements, mais la détection doit tenir compte des bits qui indiquent le signe des nombres.

L’addition de deux nombres de signes différents ne peut pas occasionner de débordement, puisque la valeur absolue du résultat sera nécessairement moindre que celle du plus grand des nombres initiaux. Un débordement ne peut donc se produire que si les deux nombres additionnés sont de même signe, deux positifs ou deux négatifs.

Prenons le cas de nombres représentés sur huit bits en complément à deux. La gamme représentable va de -128 à +127 avec un bit qui représente le signe. Si on additionne (+50)10 = (00110010)2 avec (+100)10 = (01100100)2, on aura un débordement, car $150 > 127$ . On voit dans le tableau suivant les bits qui seront produits par l’addition, avec en évidence les retenues des deux derniers niveaux. Le bit de signe a été séparé des autres.

Tableau 4 : Addition de (+50)10 + (+100)10 = (00110010)2 + (01100100)2
Retenues	0	1
		0	011 0010
		0	110 0100
		1	001 0110

Refaisons le même exercice avec deux nombres négatifs : on additionne (-50)10 = (1100 1110)2 avec (-100)10 = (1001 1100)2, qui créera aussi un débordement.

Tableau 5 : Addition de (-50)10 + (-100)10 = (1100 1110)2 + (1001 1100)2
Retenues	1	0
		1	100 1110
		1	001 1100
		0	110 1010

On peut dans les deux cas détecter le débordement en observant que la retenue du dernier niveau et la retenue de l’avant-dernier niveau sont différentes. On peut vérifier facilement que les autres cas sans débordement donnent des retenues égales. Donc, si on fait un OU-exclusif entre ces deux retenues, un résultat 1 indiquera un débordement. Ce mécanisme de détection de débordement a été ajouté au circuit additionneur/soustracteur 4 bits dans la figure suivante pour générer le signal $D$ qui indique un débordement.

Circuit additionneur/soustracteur 4 bits avec débordement.

Figure 24 : Circuit additionneur/soustracteur 4 bits avec débordement

1.8. Multiplexeur

Un multiplexeur est un circuit combinatoire qui sélectionne le signal qui provient d’une de ses entrées, et fait que sa sortie est égale à l’entrée sélectionnée. Les signaux de sélection fonctionnent typiquement selon un encodage binaire, ce qui suppose un nombre d’entrées de la forme $2^n$ . On désigne le multiplexeur par le nombre de signaux d’entrées à sélectionner.

1.8.1. Multiplexeur deux-vers-un

Le multiplexeur le plus simple utilise un seul signal de sélection $S$ qui permet de choisir une de deux entrées $I_0$ ou $I_1$ pour agir sur la sortie $Y$ .

Circuit du multiplexeur deux-vers-un.

Figure 25 : Circuit du multiplexeur deux-vers-un

Symbole du multiplexeur deux-vers-un.

Figure 26 : Symbole du multiplexeur deux-vers-un

1.8.2. Multiplexeur quatre-vers-un

Un multiplexeur quatre-vers-un permet de choisir une de quatre entrées en utilisant deux signaux de sélection. Pour simplifier la représentation symbolique, les deux signaux de sélection sont représentés comme un seul fil, qui correspond en fait à une paire de signaux $S_0$ et $S_1$ . Pour un multiplexeur à $2^n$ entrées, on aurait un vecteur de $n$ signaux de sélection.

Circuit du multiplexeur quatre-vers-un.

Figure 27 : Circuit du multiplexeur quatre-vers-un

Symbole du multiplexeur quatre-vers-un.

Figure 28 : Symbole du multiplexeur quatre-vers-un

Tableau 6 : Tableau de vérité du multiplexeur quatre-vers-un
$S_1$	$S_0$	$Y$
0	0	$I_0$
0	1	$I_1$
1	0	$I_2$
1	1	$I_3$

1.9. Décodeur

Un décodeur est un circuit combinatoire qui sert à interpréter des données encodées, le plus souvent en binaire. Il prend un groupe (vecteur) de $n$ bits en entrée, et active une sortie parmi jusqu’à $2^n$ sorties différentes. Dans le cas où certaines combinaisons d’entrées ne sont pas utilisées, moins de $2^n$ sorties peuvent être produites.

Dans un décodeur générique, chaque combinaison binaire distincte activera une seule sortie. Il y a une correspondance directe entre chaque sortie possible et un minterm d’entrée.

Circuit du décodeur trois-vers-huit.

Figure 29 : Circuit du décodeur trois-vers-huit

Tableau 7 : Tableau de vérité du décodeur trois-vers-huit
$x$	$y$	$z$	$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

1.9.1. Décodeur avec sortie active basse et signal de contrôle

On peut aussi concevoir des décodeurs basés sur des portes NAND et dont la sortie sélectionnée est active au niveau bas. Une autre fonction utile est un signal de contrôle $E$ qui n’active une sortie que lorsqu’il est activé.

Le décodeur deux-vers-quatre dont le circuit est présenté ci-dessous comporte ces deux caractéristiques. Comme on peut voir dans le tableau de vérité, tant que le signal de contrôle est inactif ( $E = 1$ puisque ce signal est également actif bas), les sorties sont inactives (au niveau 1) quelles que soient les entrées $x$ et $y$ . Lorsque $E = 0$ , une seule sortie passe à 0, selon le code binaire présent aux entrées $x$ et $y$ . Notez que ce décodeur a été conçu et étiqueté en fonction d’entrées $x$ et $y$ qui sont actives haut.

Décodeur à sortie active basse.

Figure 30 : Décodeur à sortie active basse

Tableau 8 : Tableau de vérité, décodeur 2 vers 4 avec sortie active basse
$E$	$x$	$y$	$D_0$	$D_1$	$D_2$	$D_3$
0	0	0	0	1	1	1
0	0	1	1	0	1	1
0	1	0	1	1	0	1
0	1	1	1	1	1	0
1	0	0	1	1	1	1
1	0	1	1	1	1	1
1	1	0	1	1	1	1
1	1	1	1	1	1	1

1.9.2. Implémentation de fonctions arbitraires au moyen d’un décodeur

Puisqu’un décodeur active sélectivement les $2^n$ minterms possibles à partir de ses $n$ entrées, il est possible d’implémenter, en somme de produits, une fonction quelconque en acheminant les minterms de la fonction à une porte OU. Il est même possible d’implémenter plusieurs fonctions différentes, en leur consacrant chacune une porte OU de sortie.

Voici par exemple une fonction réalisée à partir d’un décodeur trois-vers-huit. L’entrée $I$ correspond à un vecteur de trois bits. Le tableau de vérité correspondant est donné. On peut voir que les minterms choisis permettent d’implémenter

$Y = \sum(0,2,5,6)$

Fonction arbitraire réalisée au moyen d'un décodeur.

Figure 31 : Fonction arbitraire réalisée au moyen d’un décodeur

Tableau 9 : Tableau de vérité pour la fonction arbitraire
$I_2$	$I_1$	$I_0$	$Y$
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Une fonction qui comporte de nombreux minterms exige l’utilisation d’une porte OU avec un grand nombre d’entrées. Si la fonction à réaliser exige plus de $2^n/2$ minterms, il est alors plus avantageux d’implémenter le complément de la fonction, qui nécessitera moins de $2^n/2$ minterms, et d’inverser ensuite la sortie pour obtenir la fonction.

1.10. Encodeur

Un encodeur effectue le travail inverse du décodeur : lorsqu’une de ses $2^n$ (ou moins) entrées est activée, il donne le code binaire correspondant sur ses $n$ sorties vues comme un vecteur binaire. Le circuit ne nécessite pas vraiment d’entrée pour $D_0$ .

Encodeur 3 bits.

Figure 32 : Encodeur 3 bits

Tableau 10 : Tableau de vérité pour l’encodeur 3 bits
$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$	$x$	$y$	$z$
1	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	1	0	0
0	0	0	0	0	1	0	0	1	0	1
0	0	0	0	0	0	1	0	1	1	0
0	0	0	0	0	0	0	1	1	1	1

Cette configuration d’encodeur exige qu’une seule entrée soit activée à la fois. Activer plus d’une entrée ne correspond en effet à rien de valide : comment donner un sens à une telle combinaison au moyen d’un vecteur de $n$ bits? Les sorties produites alors seront des vecteurs binaires sans signification.

1.10.1. Encodeur à priorité

Un encodeur à priorité met en oeuvre une priorité entre les entrées. S’il y a plus d’une entrée 1 en même temps, la sortie sera celle qui correspond à l’entrée active qui a la plus grande priorité. Voici le tableau de vérité pour un encodeur 2 bits à priorité, dans lequel on a ajouté une sortie $V$ qui indique la validité des sorties. Si aucune entrée n’est active, $V=0$ et les sorties $x$ et $y$ ne doivent pas être prises en compte.

Lorsque des entrées sont activées, c’est celle qui a le plus grand indice qui est prioritaire.

Tableau 11 : Tableau de vérité pour encodeur 2 bits à priorité
$D_0$	$D_1$	$D_2$	$D_3$	$x$	$y$	$V$
0	0	0	0	X	X	0
1	0	0	0	0	0	1
X	1	0	0	0	1	1
X	X	1	0	1	0	1
X	X	X	1	1	1	1

Diag-K pour x.

Figure 33 : Diag-K pour $x$ de l’encodeur à priorité

Diag-K pour y.

Figure 34 : Diag-K pour $y$ de l’encodeur à priorité

En simplifiant, on trouve les expressions suivantes :

$x = D_2 + D_3$

$y = (D_1 D_2^\prime) + D_3$

$V = D_0 + D_1 + D_2 + D_3$

Encodeur 2 bits à priorité, en P de S.

Figure 35 : Encodeur 2 bits à priorité, en P de S

Puisque le terme $x = D_2 + D_3$ est déjà calculé pour $x$ , on peut le réutiliser pour construire le terme pour $V$ , tel qu’illustré ci-dessous, ce qui évite d’utiliser une porte OU à quatre entrées.

Encodeur 2 bits à priorité avec ré-utilisation d'un des termes.

Figure 36 : Encodeur 2 bits à priorité avec ré-utilisation d’un des termes

1.11. Comparateur de magnitude

Comparer la magnitude de deux nombres binaires est une opération qui peut se systématiser, comme on l’a fait pour l’addition. Considérons deux nombres binaires non signés, $A$ et $B$ de même taille $n$ , avec leurs bits respectifs $a_i$ et $b_i$ . Nous voulons que notre comparateur active une des trois sorties, selon le cas : $A < B$ , $A = B$ ou $A > B$ . Pour illustrer, nous considérerons $n = 4$ .

$a_3 a_2 a_1 a_0$

$b_3 b_2 b_1 b_0$

Nous aurons besoin d’une fonction qui permet de déterminer si deux bits sont égaux. Cette fonction correspond à la fonction Équivalence ou NOR-exclusif $a_i b_i + a_i^\prime b_i^\prime$ . Si les bits diffèrent en position $i$ , $a_i = 1$ nous permet de conclure que $A > B$ et, à l’inverse, $a_i = 0$ nous indique que $A < B$ . Nous avons ainsi les éléments qui permettent d’effectuer une comparaison pour un bit, comme on peut en voir l’implémentation sur la figure suivante.

Comparateur de magnitude.

Figure 37 : Comparateur de magnitude

Notre démarche de conception pour $n$ bits sera calquée sur la procédure que nous utilisons intuitivement pour faire une telle comparaison. La comparaison commence au niveau du bit le plus significatif. Si ces bits sont égaux, on considère la position suivante, jusqu’à atteindre une position $i$ où les bits diffèrent ou jusqu’à atteindre la fin des nombres (c’est-à-dire $i=0$ ). Si les bits diffèrent en position $i$ , $a_i = 1$ nous permet de conclure que $A > B$ , alors que $a_i = 0$ nous indique que $A < B$ .

Les signaux intermédiaires $x_i = a_i b_i + a_i^\prime b_i^\prime$ qui indiquent si deux bits d’une position sont égaux seront mis à profit pour alimenter un réseau de conditions en forme somme de produits qui mettront en application les règles énoncées. Les signaux de sortie binaires sont $(A = B), (A < B), (A > B)$ . D’une part, la régularité des opérations simplifie la conception et, d’autre part, l’implémentation sera simplifiée du fait que certains des termes nécessaires peuvent être réutilisés.

$(A = B) = x_3 x_2 x_1 x_0$

$(A < B) = a_3^\prime b_3 + x_3 a_2^\prime b_2 + x_3 x_2 a_1^\prime b_1 + x_3 x_2 x_1 a_0^\prime b_0$

$(A > B) = a_3 b_3^\prime + x_3 a_2 b_2^\prime + x_3 x_2 a_1 b_1^\prime + x_3 x_2 x_1 a_0 b_0^\prime$

On obtient ainsi un comparateur pour des nombres de quatre bits, tel qu’illustré.

Comparateur de magnitude 4 bits.

Figure 38 : Comparateur de magnitude 4 bits

1.12. Démultiplexeur

Un démultiplexeur achemine la valeur logique de son entrée à une sortie (parmi $2^n$ sorties) sélectionnée par un code binaire de sélection. Le démultiplexeur de la figure suivante comporte trois bits de sélection et permet donc d’acheminer la valeur de l’entrée $I$ vers une des huit sorties $O_i, i = 0, \ldots, 7$ . On peut aussi interpréter ce circuit comme un décodeur trois-vers-huit avec une entrée signal de contrôle (enable) $I$ .

Démultiplexeur un-vers-huit.

Figure 39 : Démultiplexeur un-vers-huit

1.13. Encodeurs divers

Il est possible de concevoir des encodeurs pour des fonctions spécialisées, comme des encodeurs pour commander des affichages. La démarche de conception s’apparente largement à celles que nous avons vues dans les exemples précédents.

1.14. Portes à trois états et tampon de bus

Les portes à trois états ajoutent un troisième état de fonctionnement aux sorties : en plus des niveaux logiques bas et haut conventionnels, un troisième état appelé haute impédance fait en sorte que la sortie se comporte comme si elle n’était plus connectée au circuit. La sortie n’agit pas sur le reste du circuit, les autres portes dont les entrées sont alimentées par la porte en haute impédance ne sont aucunement affectées par celle-ci. Pour activer cet état de sortie haute impédance, une entrée de contrôle est ajoutée.

Le figure ci-dessous montre une porte tampon à trois états. Avec Contrôle = 0, la sortie est en haute impédance; avec Contrôle = 1, la sortie est égale à l’entrée.

Porte tampon à trois états.

Figure 40 : Porte tampon à trois états

En plaçant des tampons à trois états à chaque sortie d’un décodeur, on peut réaliser un multiplexeur $n$ -vers-un en reliant les sorties des tampons à une sortie unique. Ainsi, lorsqu’une entrée est sélectionnée au moyen des entrées de sélection, c’est sa valeur qui se retrouve à la sortie du dispositif. La valeur Z représente l’état haute impédance. Lorsque l’entrée de contrôle $E = 0$ , la sortie est en haute impédance.

Tableau 12 : Tableau de vérité pour un multiplexeur quatre-vers-un trois états
$s_1$	$S_0$	$E$	$I_0$	$I_1$	$I_2$	$I_3$	$Y$
X	X	0	X	X	X	X	Z
0	0	1	$I_0$	X	X	X	$I_0$
0	1	1	X	$I_1$	X	X	$I_1$
1	0	1	X	X	$I_2$	X	$I_2$
1	1	1	X	X	X	$I_3$	$I_3$

Multiplexeur quatre-vers-un trois états.

Figure 41 : Multiplexeur quatre-vers-un trois états

La fonctionnalité trois-états permet aussi de concevoir un émetteur-récepteur de bus. Ce dispositif, illustré à la figure suivante, permet d’établir une connexion bidirectionnelle entre I/O et O/I. Lorsque l’entrée de contrôle $E = 0$ , c’est le tampon du haut de la figure qui est actif, et O/I détermine la valeur de I/O. Lorsque $E = 1$ , c’est le tampon du bas qui est actif, et I/O détermine la valeur de O/I.

Emetteur-récepteur de bus.

Figure 42 : Émetteur-récepteur de bus

Quiz de fin de chapitre

Licence

Symbole de License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International

Circuits logiques combinatoires et séquentiels Droit d'auteur © 2023 par Guy Bégin est sous licence License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, sauf indication contraire.

$A$	$C$	$B$	$D$	$I_1$	$I_2$	$F_1$
0	0	0	0	0	0	0
0	0	0	1	0	0	0
0	1	0	0	0	1	0
0	1	0	1	0	0	0
0	0	1	0	0	1	0
0	0	1	1	0	0	0
0	1	1	0	1	1	1
0	1	1	1	1	0	0
1	0	0	0	0	0	0
1	0	0	1	0	0	0
1	1	0	0	0	0	0
1	1	0	1	0	0	0
1	0	1	0	0	0	0
1	0	1	1	0	0	0
1	1	1	0	0	0	0
1	1	1	1	0	0	0

$x$	$y$	$z$	$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$	$x$	$y$	$z$
1	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	1	0	0
0	0	0	0	0	1	0	0	1	0	1
0	0	0	0	0	0	1	0	1	1	0
0	0	0	0	0	0	0	1	1	1	1

$A$	$C$	$B$	$D$	$I_1$	$I_2$	$F_1$
0	0	0	0	0	0	0
0	0	0	1	0	0	0
0	1	0	0	0	1	0
0	1	0	1	0	0	0
0	0	1	0	0	1	0
0	0	1	1	0	0	0
0	1	1	0	1	1	1
0	1	1	1	1	0	0
1	0	0	0	0	0	0
1	0	0	1	0	0	0
1	1	0	0	0	0	0
1	1	0	1	0	0	0
1	0	1	0	0	0	0
1	0	1	1	0	0	0
1	1	1	0	0	0	0
1	1	1	1	0	0	0

$x$	$y$	$z$	$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

$D_0$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$	$x$	$y$	$z$
1	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	1	0	0
0	0	0	0	0	1	0	0	1	0	1
0	0	0	0	0	0	1	0	1	1	0
0	0	0	0	0	0	0	1	1	1	1