Portes logiques

Guy Bégin

4 Portes logiques

1.1. Objectifs

Se familiariser avec les symboles usuels des portes logiques
Se familiariser avec les conventions et règles de dessin de schémas logiques
Faire la différence entre niveau de signal et valeur logique
Expliquer les différences entre le fonctionnement idéalisé et la réalité physique des portes logiques

1.2. Niveaux logiques

Une porte logique est un dispositif électronique qui implémente une fonction logique en agissant sur des signaux électriques selon une convention préétablie. En général, on établit des valeurs binaires en se basant sur la tension des signaux, en définissant une correspondance entre des gammes de tensions et les valeurs logiques 0 et 1. Par exemple, pour une tension d’alimentation $V_{DD}$ , on pourrait avoir les correspondances suivantes :

Gamme de tensions	Niveau
de 0 à $V_{DD}/3$	Niveau bas
de $2V_{DD}/3$ à $V_{DD}$	Niveau haut

Les portes logiques sont manufacturées selon différents standards technologiques qu’on appelle communément des familles logiques. Au sein d’une même famille, les portes respectent les mêmes références de niveaux pour pouvoir fonctionner ensemble adéquatement. Une porte peut comporter une ou plusieurs entrées et agit généralement sur une seule sortie.

1.3. Logique négative ou positive

On associe ensuite une valeur binaire à chacun des niveaux selon une certaine convention, par exemple :

Niveau	Valeur logique
Niveau bas	0
Niveau haut	1

qui correspond à une logique positive. La convention inverse nous donne la logique négative.

Certains signaux seront considérés comme actifs lorsque leur niveau logique sera 0. On parlera alors de signaux actifs bas. La convention implicite est généralement que les signaux sont actifs haut.

1.4. Symboles

On a défini des symboles pour représenter graphiquement les portes logiques courantes. Dans un schéma logique, les portes sont interconnectées au moyen de symboles de conducteurs (fils) qui permettent d’acheminer les valeurs logiques d’une porte à l’autre.

1.4.1. Porte ET

À deux entrées $S = A \cdot B$

Porte ET à deux entrées.

Figure 1 : Porte ET à deux entrées

Les portes qui réalisent des fonctions qui sont associatives et commutatives peuvent aussi se définir avec plus de deux entrées. C’est le cas avec les fonctions ET et OU.

À trois entrées $S = A \cdot B \cdot C$

Porte ET à trois entrées.

Figure 2 : Porte ET à trois entrées

1.4.2. Porte OU

À deux entrées $S = A + B$

Porte OU à deux entrées.

Figure 3 : Porte OU à deux entrées

1.4.3. Porte inverseur

L’opération NON qui consiste à complémenter une valeur binaire s’effectue avec une porte appelée inverseur. Il n’y a toujours qu’une entrée. $B = A^\prime$

Porte inverseur.

Figure 4 : Porte inverseur

1.4.4. Porte NON-OU (NOR)

Porte NOR à deux entrées.

Figure 5 : Porte NOR à deux entrées

1.4.5. Porte NON-ET (NAND) et NON-OU (NOR)

Les fonctions NAND et NOR ne sont pas associatives. Par exemple,

$(x \operatorname{Nor} y) \operatorname{Nor} z \neq x \operatorname{Nor} (y \operatorname{Nor} z)$

On peut néanmoins définir des versions à plusieurs entrées de ces fonctions en ajustant la priorité d’évaluation. Pour une porte NAND à trois entrées, on fera $S = (A \cdot B \cdot C)^\prime$ . Pour une porte NOR à trois entrées, on fera $(A + B + C)^\prime$ .

Porte NAND à trois entrées.

Figure 6 : Porte NAND à trois entrées

1.4.6. Entrées inversées

On utilise souvent l’élément symbolique qui est placé à la sortie de l’inverseur (un petit cercle) pour indiquer l’inversion d’une entrée ou d’une sortie d’une porte. C’est le cas à la sortie des portes NAND et NOR comme on vient de le voir. Un autre exemple est la porte NAND de la figure 7, où une des entrées est également inversée. La porte évalue donc $S = (A^\prime \cdot B \cdot C)^\prime$

porte NAND à trois entrées dont une inversée.

Figure 7 : Porte NAND à trois entrées dont une inversée

1.4.7. NAND et NOR, représentations équivalentes

En vertu du théorème de DeMorgan, on sait que $(x + y)^{\prime} = x^{\prime} y^{\prime}$ et que $(xy)^{\prime} = x^{\prime} + y^{\prime}$ . On peut donc représenter les portes NAND et NOR de deux façons équivalentes.

Deux représentations équivalentes pour une porte NAND.

Figure 9 : Deux représentations équivalentes pour une porte NAND

Deux représentations équivalentes pour une porte NOR.

Figure 8 : Deux représentations équivalentes pour une porte NOR

1.4.8. Porte OU-exclusif (XOR)

La porte XOR à deux entrées donne une sortie 1 seulement lorsque ses deux entrées sont différentes. Il est possible de définir des portes XOR à plus de deux entrées, mais il y a différentes interprétations de ce qu’une telle porte devrait avoir comme comportement. De plus, comme la réalisation pratique de cette fonction n’est pas aussi simple que pour les autres fonctions, on se retrouve la plupart tu temps à devoir mettre des portes à deux entrées en cascade pour augmenter le nombre d’entrées, ce qui rend moins intéressantes les portes XOR avec entrées nombreuses.

$S= A \cdot B^\prime + A^\prime \cdot B$

Porte XOR à deux entrées.

Figure 10 : Porte XOR à deux entrées

1.4.9. Porte NON-OU-exclusif ou Équivalence (XNOR)

La porte Équivalence produit une sortie 1 lorsque ses entrées ont la même valeur (et sont donc équivalentes). Comme pour les portes XOR, les portes XNOR à plus de trois entrées peuvent s’interpréter de différentes façons.

Porte XNOR.

Figure 11 : Porte XNOR

1.5. Universalité des NAND et NOR

En faisant appel uniquement à des portes de type NAND ou NOR, il est possible de réaliser n’importe quelle fonction logique, puisqu’il est possible de réaliser les trois opérateurs de base.

Pour réaliser un inverseur, on utilise une porte NAND à une seule entrée (ou dont toutes les entrées sont reliées ensemble).
Pour réaliser une porte ET, on fait suivre une porte NAND d’un inverseur.
Pour réaliser une porte OU, on place un inverseur devant chaque entrée d’une porte NAND .

Nous verrons plus loin qu’il est aussi possible de réaliser avantageusement des fonctions quelconques avec des portes NAND en exploitant la forme somme de produits.

1.6. Limites physiques

Les portes logiques qu’on utilisera en pratique sont des dispositifs électroniques dont le fonctionnement correspond, dans les grandes lignes, aux comportements idéalisés des modèles abstraits de l’algèbre de Boole. Mais il faut toujours garder à l’esprit que la correspondance entre modèle et réalité physique n’est jamais parfaite. En raffinant nos modèles pour y incorporer des caractéristiques, limites ou contraintes appropriées, il sera possible de mieux tenir compte de la réalité physique.

1.6.1. Sortance (Fan-out)

Le fan-out d’une porte logique mesure sa capacité à commander d’autres portes reliées à sa sortie. Puisque les portes sont des dispositifs électroniques qui doivent faire circuler un certain courant électrique pour concrétiser les niveaux de tensions qui définissent leurs valeurs d’entrée et de sortie, il y a une limite pratique à la capacité d’une porte de fournir le courant nécessaire pour faire réagir la sortie des portes qu’elle devrait commander. La sortance mesure cette limite, en nombre de portes à commander. Si on connecte plus d’entrées à une sortie que sa valeur de sortance, cette sortie ne pourra pas atteindre le niveau de tension adéquat, et les opérations logiques seront faussées.

1.6.2. Modèles de délai

Dans la mesure où on respecte ses contraintes d’utilisation, notamment de sortance, une porte logique se comporte globalement de la façon attendue, étant donné sa fonction et les conventions de niveaux de signal établies. Par exemple, le niveau signal à la sortie d’un inverseur correspondra au niveau de signal attendu pour le complément de la valeur logique à son entrée. Mais il faut garder à l’esprit que les portes sont des dispositifs électroniques, et donc physiques, sujets à des «imperfections» qui diffèrent du comportement idéalisé.

Une de ces «imperfections» dont on doit impérativement tenir compte est le délai de propagation qui se manifeste comme un retard entre le moment où le signal à l’entrée de la porte assume (se stabilise à) son niveau de signal et le moment où la sortie de la porte atteint son niveau de signal attendu. C’est en quelque sorte le délai entre une action à l’entrée et son effet sur la sortie. Ce délai limite la vitesse à laquelle on peut utiliser notre circuit logique. Si on essaie d’effectuer des transitions plus rapides que le délai, le comportement ne sera plus conforme aux attentes de conception. On doit donc respecter une vitesse de commutation maximale imposée par les délais de propagation.

Le délai de propagation peut dépendre de plusieurs facteurs : la famille logique, le type de porte, le sens de la transition, la sortance effective, les caractéristiques d’interconnexions, etc. Pour faciliter l’analyse, on fait appel à des modèles de délais plus ou moins sophistiqués. Un modèle très simple consiste à supposer un délai de propagation moyen, constant pour toutes les portes d’une famille donnée. Un modèle un peu plus subtil pourrait prendre en compte des délais de propagation moyens différents par types de portes. Le délai de propagation moyen est une caractéristique clé qui différencie les différentes familles logiques. Les délais sont typiquement de l’ordre de nanosecondes, permettant des vitesses de commutation dans les dizaines, centaines, voire des milliers de MHz.

Lorsqu’un signal doit se propager à travers plusieurs portes, les délais de propagation s’accumulent, limitant encore davantage la vitesse de commutation de l’ensemble du circuit. La vitesse qui pourra être atteinte pour l’ensemble d’un circuit sera typiquement déterminée par le plus lent chemin (c’est-à-dire celui qui cumule le plus long temps de propagation).

Modèles simples

À titre d’exemple, considérons une porte ET à deux entrées 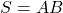$S = A B$ . Le modèle le plus simple suppose une porte idéale, sans aucun délai : le chronogramme suivant montre la sortie qui commute immédiatement lorsque les conditions d’entrée changent.

Figure 12 : Porte ET sans délai
1. Modèle avec délai en sortie
  
  Le modèle avec délai en sortie consiste à considérer un délai fixe, qui affecte la sortie de la porte : la commutation prend effet en sortie après un délai $t_p$ .
  
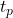  Figure 13 : Porte ET avec délai en sortie
2. Modèle avec délai en entrée
  
  Le modèle avec délai en entrée est plus nuancé, car il permet de spécifier un délai différent selon l’entrée qui entraîne le changement à la sortie.
  
  Figure 14 : Porte ET avec délai aux entrées
3. Modèle combiné
  
  Le modèle combiné consiste à considérer des délais différents par entrée et en plus, un délai global en sortie.
Condition de course et aléas

Un autre effet néfaste potentiel des délais à considérer est ce qu’on appelle une condition de course. Considérons le circuit de la figure 15. La sortie de la porte est 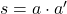$s = a \cdot a^\prime$ qui devrait normalement donner systématiquement 0. Mais le chemin menant de l’entrée $a$ à l’entrée du haut de la porte ET est plus court (en termes de délais) que le chemin qui mène à l’entrée du bas. 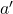En effet, le signal $a^\prime$ est retardé d’un délai de propagation 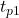$t_{p1}$ par rapport à $a$ .

Figure 15 : Cas à risque de condition de course

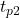En pratique, on pourrait observer un chronogramme qui s’apparente à celui de la figure suivante (figure 16), où on voit que les deux signaux à l’entrée de la porte ET sont simultanément égaux à 1 pendant une courte période. Une courte impulsion 1 sera donc générée sur le signal $s$ en sortie de la porte ET, après le délai de propagation $t_{p2}$ de celle-ci. Cette impulsion, qui ne correspond à rien selon la logique du circuit est appelée un aléa (ou en anglais, glitch).

Figure 16 : Chronogramme montrant une condition de course

Ces aléas peuvent être la source de problèmes et de dysfonctionnements qui sont parfois difficiles à diagnostiquer, et il faut vraiment s’en méfier. Une telle impulsion, quasi imperceptible, pourrait par exemple déclencher le basculement de la valeur d’une cellule mémoire plus loin dans le circuit.

1.6.3. Porte tampon

La valeur binaire à la sortie d’une porte tampon est la même qu’à l’entrée. La porte n’agit pas sur la valeur logique mais permet de reconditionner le signal à son entrée pour le rendre, en sortie, davantage conforme aux niveaux électriques de référence. Une porte tampon est essentiellement utilisée pour renforcer et stabiliser le niveau du signal. Une façon pratique de réaliser une porte tampon est de placer deux inverseurs l’un à la suite de l’autre. L’utilisation de portes tampons est un des moyens de s’assurer de respecter les conditions de sortance.

Quiz de fin de chapitre

Faites glisser les identifications de fonctions sur les schémas de portes logiques.

Licence

Symbole de License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International

Circuits logiques combinatoires et séquentiels Droit d'auteur © 2023 par Guy Bégin est sous licence License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, sauf indication contraire.