2 Logique binaire, fonctions logiques et algèbre de Boole
1.1. Objectifs
- Situer les opérations de la logique binaire dans leur contexte algébrique
- Se familiariser avec les postulats de l’algèbre de Boole, et les principaux théorèmes
- Exprimer une fonction logique par un tableau de vérité
- Formuler une expression logique à partir d’un tableau de vérité
- Exprimer une fonction logique en somme de produits, ou en produit de sommes, et convertir d’une forme à l’autre
1.2. Logique binaire
La logique binaire associe une valeur de vérité à des variables, selon une convention préétablie. Ces valeurs de vérité sont binaires, à savoir vrai ou faux. Pour représenter ces valeurs de vérité, on peut utiliser un encodage binaire, par exemple
| Valeur de vérité | Valeur binaire | |
|---|---|---|
| Vrai | 1 | |
| Faux | 0 |
1.2.1. Variable binaire
Une variable binaire, dénotée par une lettre, permet de désigner une valeur binaire pouvant assumer une des deux valeurs possible, 0 ou 1. La variable est typiquement associée à une proposition, l’état d’un élément ou à toute autre condition pouvant admettre deux états distincts. En assignant une valeur binaire à la variable, on définit une valeur de vérité associée à cette variable, et ainsi à la condition qu’elle représente. Par exemple, soit ![]() une variable binaire qui représente la proposition «le soleil est visible». Alors,
une variable binaire qui représente la proposition «le soleil est visible». Alors, ![]() peut s’interpréter comme «le soleil est visible est faux» ou «le soleil n’est pas visible».
peut s’interpréter comme «le soleil est visible est faux» ou «le soleil n’est pas visible».
1.2.2. Opérations logiques
Trois opérations logiques de base permettent d’agir sur des variables binaires, de les combiner et de formuler des expressions logiques à partir d’elles.
- ET : cette opération est représentée (comme la multiplication) par un point central ou par l’absence de signe d’opérateur entre les arguments. Par exemple,
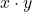 ou
ou 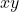 . La valeur de l’expression est 1 si et seulement si toutes les variables ont la valeur 1. Sinon, la valeur est 0.
. La valeur de l’expression est 1 si et seulement si toutes les variables ont la valeur 1. Sinon, la valeur est 0. - OU : cette opération est représentée (comme l’addition) par un signe +. Par exemple,
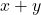 . La valeur de l’expression est 1 si au moins une des variables a la valeur 1. Si aucune des variables ne vaut 1, la valeur de l’expression est 0.
. La valeur de l’expression est 1 si au moins une des variables a la valeur 1. Si aucune des variables ne vaut 1, la valeur de l’expression est 0. - NON : cette opération est représentée par un prime, par exemple
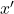 , ou par une barre au-dessus de la variable,
, ou par une barre au-dessus de la variable, 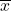 . L’opération NON renverse la valeur binaire de son argument : si
. L’opération NON renverse la valeur binaire de son argument : si 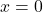 alors
alors 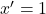 ; si
; si 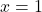 alors
alors 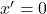 . Cette opération de négation, est aussi appelée complément, car complémenter une valeur binaire revient à faire basculer sa valeur.
. Cette opération de négation, est aussi appelée complément, car complémenter une valeur binaire revient à faire basculer sa valeur.
1.2.3. Expression logique
Une expression logique combine des variables logiques et des opérations et peut donc assumer une valeur binaire logique. Cette valeur logique peut être assignée à une autre variable, en créant ainsi une équation logique. Par exemple, ![]() signifie que
signifie que ![]() assume la valeur de l’expression
assume la valeur de l’expression ![]() . À partir des valeurs logiques des variables (entrées)
. À partir des valeurs logiques des variables (entrées) ![]() et
et ![]() , on peut donc déterminer la valeur logique de la sortie
, on peut donc déterminer la valeur logique de la sortie ![]() .
.
1.2.4. Tableaux de vérité
On peut décrire la valeur logique d’une variable de sortie en fonction des valeurs possibles des variables d’entrée au moyen d’un tableau de vérité. Dans un tel tableau, il y a une ligne pour chaque combinaison possible des valeurs d’entrée et, sur chaque ligne, on indique la valeur de sortie correspondante. C’est en quelque sorte une description en extension de la valeur de l’expression de sortie.
Voici par exemple les tableaux de vérité pour les opérations de base.
Opération ET :
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Opération OU :
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
Opération complément :
| 0 | 1 | |
| 1 | 0 |
1.3. Formalisme mathématique
Un formalisme mathématique, élaboré bien avant l’avènement des circuits électroniques numériques, permet de formuler, analyser et simplifier les expressions de la logique binaire. Il s’agit de l’algèbre de Boole.
1.3.1. Définitions
Une algèbre est un système mathématique, défini pour un ensemble d’éléments auxquels sont associés un ensemble d’opérateurs et qui respecte un jeu d’axiomes ou postulats. Une algèbre nécessite donc :
- Un ensemble
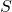 d’éléments
d’éléments - Des opérateurs :
 ,
,  ,
, 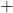
- L’application des opérateurs aux différents éléments doit respecter un certain nombre de propriétés appelées postulats, comme :
- Fermeture
- Associativité
- Commutativité
- Existence d’élément identité
- Existence d’élément inverse
- Distributivité
Selon le choix des postulats, on arrive à définir différents types de systèmes algébriques. Par exemple, les nombres réels qui nous sont familiers constituent un système algébrique d’un type appelé corps.
1.4. Algèbre de Boole
Une algèbre de Boole est un type de système algébrique défini sur un ensemble ![]() , muni de deux opérateurs dénotés
, muni de deux opérateurs dénotés ![]() et
et ![]() , et qui respecte les postulats suivants1 (postulats de Huntington) :
, et qui respecte les postulats suivants1 (postulats de Huntington) :
- Fermeture : tout résultat d’une opération sur un élément de l’ensemble donne un élément de l’ensemble.
- ♠ Fermeture par rapport à
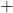 .
. - ♥ Fermeture par rapport à
 .
.
- ♠ Fermeture par rapport à
- Éléments identité
- ♠ Élément identité de
 , noté 0 : on a
, noté 0 : on a 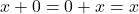 .
. - ♥ Élément identité de
 , noté 1 : on a
, noté 1 : on a 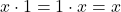 .
.
- ♠ Élément identité de
- Commutativité
- ♠ Commutativité par rapport à
 : on a
: on a 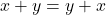 .
. - ♥ Commutativité par rapport à
 : on a
: on a 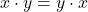 .
.
- ♠ Commutativité par rapport à
- Distributivité
- ♠
 est distributif sur
est distributif sur 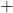 : on a
: on a 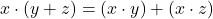 .
. - ♥
 est distributif sur
est distributif sur  : on a
: on a 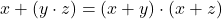 .
.
- ♠
- Pour chaque élément
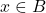 , il existe un élément
, il existe un élément 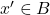 (appelé complément de
(appelé complément de 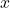 ) tel que
) tel que
- ♠
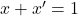 .
. - ♥
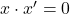 .
.
- ♠
- Il existe au moins deux éléments
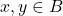 tels que
tels que 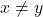 .
.
Observons des différences entre une algèbre de Boole et le corps des réels :
- Il n’y a pas de loi d’associativité dans les postulats. On peut en démontrer une, cependant.
- L’opération
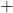 est distributive sur
est distributive sur  .
. - Il n’y a pas d’inverse multiplicatif ni d’inverse additif, on ne peut donc pas faire de soustraction ou de division.
- Il y a un concept de complément.
- L’ensemble d’éléments est différent. Nous utiliserons pour notre part l’ensemble
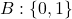 pour notre algèbre de Boole.
pour notre algèbre de Boole.
1.5. Algèbre de Boole à deux valeurs
L’ensemble de définition : ![]() .
.
Opérateur ![]()
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Opérateur ![]()
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
Règle de complémentation
| 0 | 1 | |
| 1 | 0 |
1.6. Vérification des postulats
- La fermeture est évidente (en regardant les tableaux des opérations).
- En observant les tableaux de vérité, on constate que
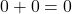 ,
, 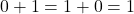
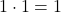 ,
, 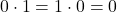
ce qui définit les deux éléments identité : 0 pour
 et 1 pour
et 1 pour  .
. - La commutativité des lois est évidente : les tableaux sont symétriques.
- Les lois de distributivité se démontrent aisément en établissant des tableaux de vérité pour les différentes valeurs de
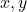 et
et  .
. - Par le tableau de complément, on vérifie que
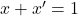 , car
, car 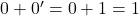 et
et 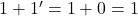
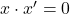 car
car 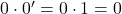 et
et 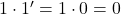 .
.
- Le postulat 6 est vérifié car il y a deux éléments distincts : 0 et 1.
Notes de bas de page :
Certains postulats viennent en paires; nous les distinguons ici au moyen d’étiquettes ♠ ou ♥.

