14 Exercices
Série 1
Question
Effectuez la conversion des nombres suivants dans la base demandée:
Réponse
Question
Donnez le nombre minimum de bits nécessaires pour définir un code pour
représenter:
- les chiffres de 0 à 9
- les nombres de -17 à 17
- les lettres A … Z et les chiffres 0 … 9
- alphanumérique pour les lettres A … Z, a … z et les
chiffres 0 … 9
Réponse
- 4 bits.
- 6 bits.
- 6 bits.
- 6 bits.
Question
Calculez les compléments suivants (pour un nombre de bits ![]() ):
):
- complément à deux de
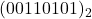 en supposant
en supposant 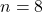
- complément à un de
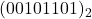 en supposant
en supposant 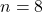
- complément à cinq de
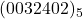 en supposant
en supposant 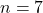
- complément à 2 de
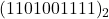 en supposant
en supposant 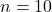
- complément à 2 de
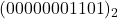 en supposant
en supposant 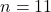
Réponse
Question
Effectuez les calculs suivants selon la méthode indiquée:
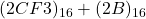 , (add. directe base 16). Réponse:
, (add. directe base 16). Réponse: 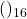
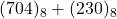 , add. directe base 8, conversion). Réponse:
, add. directe base 8, conversion). Réponse: 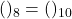
 , complément à 2, conversion. Réponse:
, complément à 2, conversion. Réponse: 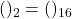
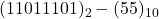 , complément à 2. Réponse:
, complément à 2. Réponse: 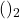
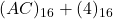 par addition directe en base 16. Réponse:
par addition directe en base 16. Réponse: 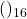
 en utilisant le complément à 1 en base 2. Réponse:
en utilisant le complément à 1 en base 2. Réponse: 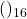
 en utilisant le complément à 2 en base 2. Réponse:
en utilisant le complément à 2 en base 2. Réponse: 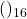
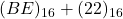 , (add. directe base 16). Réponse:
, (add. directe base 16). Réponse: 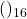
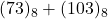 , add. directe base 8, conversion). Réponse:
, add. directe base 8, conversion). Réponse: 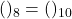
 , compl. à 2. Réponse:
, compl. à 2. Réponse: 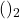
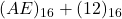 , (add. directe base 16). Réponse:
, (add. directe base 16). Réponse: 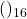
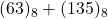 , add. directe base 8, conversion). Réponse:
, add. directe base 8, conversion). Réponse: 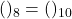
Réponse
Question
Vous disposez de blocs permettant de calculer les fonctions suivantes:
- C4
- complément à un d’un nombre de 4 bits
- ADD4
- addition de deux nombres de 4 bits, avec entrée pour
retenue et retenue de sortie.
Indiquez par un schéma-bloc comment on peut relier ces blocs pour
calculer:
- le complément à deux d’un nombre de 4 bits
- le complément à deux d’un nombre de 8 bits
- la somme de deux nombres de 8 bits
- la soustraction de nombres de 4 bits
Réponse
Question
Un réseau informatique comporte 60 ordinateurs. On doit assigner à
chacun de ces ordinateurs un mot de code binaire unique.
- Combien de bits par mot sont nécessaire pour la codification?
- Combien de mots de code ne seront pas utilisés?
Réponse
- 6 bits
- 4 mots
Question
Donnez le nombre minimum de bits nécessaires pour définir un code pour représenter
- les jours de la semaine
- les jours du mois
- les jours dans l’année (nombre entre 1 et 365)
- les jours de l’année (mois et date)
- une date de naissance (jour, mois, année)
Réponse
- 3 bits
- 5 bits
- 10 bits
- 4 bits pour le mois et 5 bits pour la date, alors 9 bits au total.
- En supposant une année comprise entre 0 et 2048: 12 bits pour
l’année et 9 pour jour/mois, donc un total de 21 bits.
Série 2
Question
La fonction logique à trois entrées ![]() donnée par son
donnée par son
tableau de vérité:
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
doit être implémentée par un circuit logique.
- Donnez l’expression de cette fonction:
- Selon la première forme canonique (
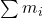 )
) - Selon la deuxième forme canonique (
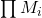 )
)
- Selon la première forme canonique (
- Trouvez une expression simplifiée pour la fonction en utilisant les
théorèmes de l’algèbre de Boole. - Dessinez le circuit logique correspondant à l’expression simplifiée
trouvée.
Réponse
-
- Première forme canonique
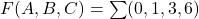
- Première forme canonique
![]()
![]()
- Deuxième forme canonique
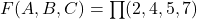
![]()
![]()
Question
Trouvez le complément de la fonction logique donnée par l’expression
suivante, en utilisant trois méthodes différentes.
![]()
Réponse
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
![]()
![]()
Question
Considérez la fonction logique définie par l’expression ![]() .
.
- Dessinez le circuit logique correspondant.
- Dessinez un circuit équivalent qui n’utilise que des portes NAND.
- Dessinez un circuit équivalent qui n’utilise que des portes NOR.
Réponse
Question
On doit concevoir un circuit logique qui détermine le complément à deux
d’une entrée ![]() binaire (signée) de 4 bits notés
binaire (signée) de 4 bits notés
![]() . Il y aura donc 4 bits de sortie,
. Il y aura donc 4 bits de sortie, ![]() . En considérant chacun des bits de sortie comme une
. En considérant chacun des bits de sortie comme une
fonction des quatre bits d’entrée, par ex. ![]() ,
,
donnez les tableaux de vérité pour ![]() , et
, et ![]() .
.
Réponse
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Question
Complétez la figure ci-dessous (en ajoutant des connexions) afin de
réaliser la fonction
![]()
Réponse
Question
Complétez la figure ci-dessous (en ajoutant des connexions) afin de
réaliser une fonction dont la sortie est
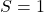 lorsque l’entrée est
lorsque l’entrée est 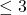 ou impaire
ou impaire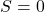 dans les autres cas.
dans les autres cas.
L’entrée ![]() représente un nombre entier décimal
représente un nombre entier décimal
codé en BCD. Les entrées ![]() peuvent donner n’importe quelle
peuvent donner n’importe quelle
sortie.
Réponse
Question
Dessinez le circuit logique de la fonction ![]() en utilisant au plus quatre portes NAND.
en utilisant au plus quatre portes NAND.
Réponse
Question
Simplifiez la fonction logique donnée par l’expression suivante:
![]()
au moyen d’un diagramme de Karnaugh. Identifiez sur le diagramme les
regroupements essentiels, les regroupements absolument inutiles et
les regroupements pour lesquels on a le choix. Donnez deux solutions
aussi simplifiées.
Réponse
![]()
![]()
Question
Considérez la fonction logique définie par l’expression
![]()
- Dessinez le circuit logique correspondant.
- Dessinez un circuit équivalent qui n’utilise que des portes
NAND. - Dessinez un circuit équivalent qui n’utilise que des portes
NOR. - Dessinez un circuit équivalent qui ne comporte que trois niveaux de
portes (incluant les inversions).
Réponse
Question
Simplifiez la fonction logique donnée par l’expression suivante:
![]()
au moyen d’un diagramme de Karnaugh. Donnez deux solutions aussi simplifiées.
Réponse
![]()
![]()
Question
Considérez la fonction logique définie par l’expression ![]() .
.
- Dessinez le circuit logique correspondant.
- Dessinez un circuit équivalent qui n’utilise que des portes
NAND. - Dessinez un circuit équivalent qui n’utilise que des portes
NOR. - Dessinez un circuit équivalent qui ne comporte que deux niveaux de
portes (excluant les inversions).
Réponse
Question
Donnez le tableau de vérité des deux fonctions qui, à partir d’une
entrée binaire non-signée sur trois bits, donnent en sortie la
représentation binaire non-signée sur deux bits du plus grand diviseur
![]() de l’entrée, s’il y a lieu. Simplifiez les deux fonctions en
de l’entrée, s’il y a lieu. Simplifiez les deux fonctions en
tenant compte des cas facultatifs.
Réponse
| 0 | 0 | 0 | x | x | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 |
Question
Complétez la figure ci-dessous (en ajoutant des connexions) afin de
réaliser une fonction NAND à trois entrées ![]() .
.
Réponse
Question
Dans une application numérique, on doit concevoir un circuit logique
qui permet de détecter les nombre composés, qui peuvent être
décomposés en facteurs (nombres qui ne sont pas premiers. Le circuit
doit donner une sortie 1 quand un nombre composé est présenté à
l’entrée; par exemple, le circuit doit donner 1 pour une entrée 4
(0100) et 0 pour une entrée 3 (0011). Les nombres 0 et 1 seront
considérés comme des cas facultatifs.
- Donnez le tableau de vérité pour réaliser cette application pour un
mot d’entrée (non-signé) de quatre bits,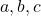 et
et 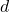 .
. - Au moyen d’un diagramme de Karnaugh, trouvez une expression logique
simplifiée pour cette fonction logique et ne représentez que les
impliquants premiers retenus pour la solution. - Donnez le schéma du circuit logique qui implémente cette fonction
en somme de produit à l’aide de portes NON-ET (pas de restrictions
sur le nombre d’entrées).
Réponse
- Tableau de vérité
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 |
- Diagramme de Karnaugh
- Schéma du circuit
Série 3
Question
À l’aide d’un diagramme de Karnaugh, simplifiez
![]()
en produit de sommes.
Réponse
![]()
Question
À l’aide d’un diagramme de Karnaugh, simplifiez
![]()
en tenant compte des cas facultatifs suivants: ![]() .
.
Donnez une solution qui n’utilise pas l’entrée ![]() .
.
Réponse
- Diagramme de Karnaugh
![]()
Question
À l’aide de la méthode Quine-McCluskey, simplifiez l’expression
logique suivante:
![]()
Tenez compte des cas facultatifs suivants:
![]()
Réponse
| 011110 | 011111 | 101111 | 111110 | 011010 | 011101 | 111100 | 111111 | ||
|---|---|---|---|---|---|---|---|---|---|
| 011-10 | X | X | |||||||
| 0111-0 | X | X | |||||||
| 1111-0 | X | X | |||||||
| -11111 | X | X | |||||||
| 1-1111 | X | X | |||||||
| -1111- | X | X | X | X |
i.p.e. = −1111−, 1−1111
i.p.i. = 011−10, 0111−0, 1111−0, −11111
Question
Complétez la figure ci-dessous pour obtenir un multiplicateur dont
la sortie (5 bits) est le produite de deux entrées (de 3 bits et 2
bits, respectivement). Comme on peut voir sur la figure, on dispose
de quatre additionneurs complets à 1 bit et de six portes ET. La
multiplication sera
![]()
Réponse
Question
Considérez la fonction logique ![]() définie par le tableau de vérité suivant
définie par le tableau de vérité suivant
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Vous devez réaliser cette fonction au moyen d’un multiplexeur à huit
entrées sans utiliser la variable ![]() dans les lignes de
dans les lignes de
sélection. Complétez le tableau de réalisation et la figure
ci-dessous.
| 0 | ||||||||
| 1 |
Réponse
| 0 | X | X | X | X | ||||
| X | ||||||||
| X | ||||||||
| 1 | X | X |
Question
Simplifiez la fonction logique à six entrées
![]()
représentée par la liste de minterms suivants
010000, 101000, 110100, 110101, 110110, 111100
en tenant compte des cas facultatifs représentés par les minterms
suivants
000000, 001100, 000111, 101001, 110111
par la méthode de Quine-McCluskey. Vous devez donner le détail de
toutes les étapes, remplir les tableaux de couverture initial et
réduit, identifier les impliquants premiers essentiels (i.p.e.), les
impliquants premiers absolument inessentiels (i.p.a.i.) et les
impliquants premiers inessentiels tout court (i.p.i.). Donnez la
solution sous la forme d’une expression en ![]() .
.
Réponse
| 010000 | 101000 | 110100 | 110101 | 111100 | 110110 | 000000 | 001100 | 000111 | 101001 | 110111 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 001100 | X | |||||||||||
| 000111 | X | |||||||||||
| 0−0000 | X | X | ||||||||||
| 10100− | X | X | ||||||||||
| 11−100 | X | X | ||||||||||
| 1101−0 | X | X | ||||||||||
| 1101−− | X | X | X | X |
i.p.e. = 1101−−, 1101−0, 10100−, 0−0000
i.p.a.i. = 11−100, 000111, 001100
Question
Réalisez les fonctions logiques suivantes au moyen d’un multiplexeur
quatre-vers-un.
Réponse
Question
Identifiez la fonction réalisée par le circuit ci-dessous, en donnant
la liste des minterms en fonction des entrées ![]() et
et ![]() .
.
Réponse
![]()
Question
Un circuit combinatoire est défini par les trois fonctions logiques
suivantes. Dessinez un circuit réalisant ces trois fonctions en
utilisant un décodeur constitué de portes NAND (vous devez dessiner
le schéma du décodeur), et des portes NAND et ET
externes.
![]()
![]()
![]()
Réponse
Question
Simplifiez la fonction donnée par l’expression suivante
![]()
en considérant les cas facultatifs suivants
![]()
par la méthode de Quine-McCluskey. Vous devez
donner le détail de toutes les étapes, identifier à la fin les
impliquants premiers essentiels (i.p.e.), les impliquants premiers
absolument inessentiels (i.p.a.i.) et les impliquants premiers
inessentiels tout court (i.p.i.). et donner la solution finale avec
les variables.
Réponse
| 0011 | 1001 | 1110 | 1111 | 0100 | 1100 | 1010 | ||
|---|---|---|---|---|---|---|---|---|
| 0011 | X | |||||||
| 1001 | X | |||||||
| 1010 | X | |||||||
| −100 | X | X | ||||||
| 11−0 | X | X | ||||||
| 111− | X | X |
i.p.e. = 111−, 1001, 0011
i.p.a.i. = 11−0, −100, 11−0
Question
Concevez un circuit qui permet de comparer deux mots de 3 bits et qui
donne 1 lorsqu’ils sont égaux et 0 sinon. Vous devez utiliser des
portes XOR et d’autres portes.
Réponse
Question
La fonction logique à quatre entrées ![]() donnée par
donnée par
son tableau de vérité:
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 1 | |
| 0 | 0 | 1 | 0 | X | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | X | |
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0 | X | |
| 1 | 1 | 1 | 1 | 1 |
doit être implémentée par un circuit logique.
- Simplifiez la description de cette fonction en utilisant un diagramme de Karnaugh.
- Trouvez le tableau de couverture pour la fonction et réduisez-le en tableau réduit.
- Identifiez les impliquants premiers essentiels (i.p.e.), les
impliquants premiers absolument inessentiels (i.p.a.i.) et les
impliquants premiers inessentiels tout court (i.p.i.). - Dessinez le circuit logique simplifié, réalisé en n’utilisant que des portes NAND.
Réponse
- Diagramme de Karnaugh
![Rendered by QuickLaTeX.com \[ S = A^{\prime}C^{\prime}D + BCD + AB^{\prime}D \]](https://pressbooks.etsmtl.ca/app/uploads/quicklatex/quicklatex.com-305d700b8b7c953a3a98ad5a6cdc0407_l3.png)
- Tableau de couverture:
| 0001 | 0101 | 0111 | 1001 | 1011 | 1111 | 0010 | 1000 | 1110 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0010 | X | |||||||||
| 0−01 | X | X | ||||||||
| −001 | X | X | ||||||||
| 100− | X | X | ||||||||
| 01−1 | X | X | ||||||||
| 10−1 | X | X | ||||||||
| −111 | X | X | ||||||||
| 1−11 | X | X | ||||||||
| 111− | X | X |
Tableau de couverture réduit:
| 0001 | 0101 | 0111 | 1001 | 1011 | 1111 | 0010 | 1000 | 1110 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0−01 | X | X | ||||||||
| −001 | X | X | ||||||||
| 01−1 | X | X | ||||||||
| 10−1 | X | X | ||||||||
| −111 | X | X | ||||||||
| 1−11 | X | X |
- i.p.e. = 0-01, 10-1,-111 i.p.a.i. = 0010,100-,111-i.p.i. = 1-11, 01-1, -001
Question
Un circuit combinatoire est défini par les trois fonctions logiques
suivantes. Dessinez un circuit réalisant ces trois fonctions en
utilisant un décodeur et des portes externes.
![]()
![]()
![]()
Réponse
Question
Identifiez la fonction logique ![]() définie par le circuit
définie par le circuit
logique suivant:
- Donnez son tableau de vérité.
- Donnez la forme canonique somme de produits de cette fonction.
Réponse
- Tableau de vérité
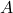
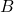
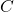
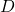
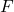
0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 1 1 0 0 1 0 0 0 0 1 0 1 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 0 1 0 0 1 0 1 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 - Forme canonique
![Rendered by QuickLaTeX.com \[ F (A, B, C, D) = \sum m(0, 2 , 5, 7, 8, 9, 14, 15) \]](https://pressbooks.etsmtl.ca/app/uploads/quicklatex/quicklatex.com-f5af89a7801220dafd8a84971a11bc9b_l3.png)
Question
Trouvez l’expression minimale pour les deux fonctions suivantes,
sachant qu’elles doivent être implémentées dans un même
circuit. Utilisez la méthode Quine-McCluskey.
![]()
![]()
Réponse
![]()
![]()
Question
La fonction logique à trois entrées ![]() représentée par
représentée par
le tableau de vérité:
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
doit être implémentée par un circuit logique.
- Donnez l’expression de cette fonction:
- Selon la première forme canonique (
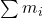 )
) - Selon la deuxième forme canonique (
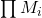 )
)
- Selon la première forme canonique (
- Trouvez une expression simplifié pour cette fonction en utilisant
un diagramme de Karnaugh en format horizontal. - Donnez l’expression du complément de cette fonction:
- Selon la première forme canonique (
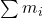 )
) - En complémentant votre expression simplifiée au moyen du
théorême de DeMorgan.
- Selon la première forme canonique (
- Dessinez le circuit logique à partir de l’expression simplifiée
trouvée.
Réponse
Question
Simplifiez la fonction logique donnée par la forme canonique
suivante:
![]()
au
moyen d’un diagramme de Karnaugh (la numérotation des termes est en
hexadécimal). Identifiez sur le diagramme les regroupements
essentiels, les regroupements absoluments inutiles et les
regroupements pour lesquels on a le choix. Donnez deux solutions
aussi simplifiées.
Réponse
Les regroupements essentiels: orange, mauve, bleu, vert.
Le regroupement jaune est absolument inutile.
![]()
![]()
Question
Considérez la fonction logique définie par l’expression
![]()
- Dessinez le circuit logique correspondant.
- Dessinez un circuit équivalent qui n’utilise que des portes
NAND. - Dessinez un circuit équivalent qui n’utilise que des portes
NOR. - Dessinez un circuit équivalent qui ne comporte que 3 niveaux de
portes (incluant les inversions).
Réponse
Question
Donnez le tableau de vérité pour les fonctions logiques correspondant
à:
Réponse
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 |
Question
Considérez la fonction logique donnée par l’expression suivante:
![]()
Les cas suivants sont facultatifs:
![]()
- Simplifiez cette expression logique par la méthode de
Quine-McCluskey, en tenant compte des cas facultatifs. Identifiez
clairement les implicants essentiels et non-essentiels. - Dessinez un réseau logique qui réalise votre expression logique
simplifiée en n’utilisant que des portes NAND.
Réponse
| 00000 | 10000 | 00100 | 10001 | 10100 | 01110 | 11001 | 10101 | 10111 | 00001 | 00101 | 11011 | 11101 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −0−0− | X | X | X | X | X | X | X | X | ||||||
| 01110 | X | |||||||||||||
| 101−1 | X | X | ||||||||||||
| 110−1 | X | X | ||||||||||||
| 1−−01 | X | X | X | X |
i.p.e. = -0-0-, 01110, 101-1, 1–01
i.p.a.i = 110-1
- Réseau logique
Question
Vous devez concevoir un circuit logique combinatoire qui calcule la
valeur absolue d’un nombre de 4 bits signé en complément à deux. Les
seules valeurs d’entrée possibles sont donc de -7 à 7 inclusivement,
les autres nombres seront considérées comme des cas facultatifs. Vous
disposez de composants programmables pour réaliser cette fonction.
- Réalisez votre circuit logique combinatoire en utilisant un PROM à
quatre entrées et deux sorties tel qu’illustré. Vous devez mettre
des croix aux endroits où vous voulez que les connections soient
effectuées (dans la section programmable).
- Réalisez votre circuit logique combinatoire en utilisant le PAL à
quatre entrées et trois sorties tel qu’illustré. Vous devez mettre
des croix aux endroits où vous voulez que les connections soient
effectuées (dans la section programmable).
Réponse
Question
Considérez le circuit logique ci-dessous. Le signal ![]() passe de 0 à 1
passe de 0 à 1
l’instant 15 ns; le signal ![]() passe de 1 à 0 à l’instant 15 ns; le
passe de 1 à 0 à l’instant 15 ns; le
signal ![]() passe de 1 à 0 à l’instant 60 ns.
passe de 1 à 0 à l’instant 60 ns.
- Complétez un chronogramme qui montre les traces pour chacun des
signaux d’entrée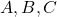 et de sortie
et de sortie 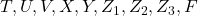 , en supposant un temps de propagation de 10 ns
, en supposant un temps de propagation de 10 ns
pour toutes les portes. Identifiez clairement sur le
chronogramme les temps de propagation et les éventuels problèmes
(glitchs) occasionnés par les délais. - Identifiez la fonction logique réalisée par ce circuit logique.
- Déterminer le délai de propagation (des entrées à la sortie)
maximal pour ce circuit, et précisez le chemin critique. - Si ce circuit doit être utilisé à répétition, de façon périodique,
quelle est la plus courte période qu’on puisse utiliser tout en
étant sûr que le circuit fonctionne correctement. - On désire remplacer ce circuit par un circuit à trois niveaux
logiques. Donnez le schéma d’un circuit en forme somme de produit
qui remplit la même fonction. - Donnez le délai de propagation maximal pour le nouveau circuit
somme de produit.
Réponse
- Chronogramme
- Fonction logique
![Rendered by QuickLaTeX.com \[ F = A \oplus B \]](https://pressbooks.etsmtl.ca/app/uploads/quicklatex/quicklatex.com-ac847d288e9cd157b1192cc8531c8f7f_l3.png)
- Délai de longueur 4, en passant par
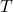 ,
, 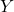 et
et 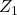 .
. - On doit attendre le temps d’un délai de propagation pour être
certain que le circuit fonctionne correctement. - Délai de longueur 3.
Série 4
Question
Construisez un décodeur 5-vers-32 en utilisant quatre décodeurs
3-vers-8 avec entrée enable.
Réponse
Question
Vous devez concevoir un encodeur à priorité à quatre
entrées. L’entrée ![]() doit avoir la plus grande priorité et
doit avoir la plus grande priorité et
l’entrée ![]() doit avoir la plus faible priorité, avec la
doit avoir la plus faible priorité, avec la
priorité des autres entrées qui suivent le même ordre. Les sorties
seront ![]() et
et ![]() qui indique la validité des sorties:
qui indique la validité des sorties:
![]() si toutes les entrées sont à 0;
si toutes les entrées sont à 0; ![]() si au moins une
si au moins une
entrée est 1.
Réponse
Question
Un circuit séquentiel à deux bascules D, ![]() et
et ![]() , comporte
, comporte
deux entrées ![]() et
et ![]() et une sortie
et une sortie ![]() . Les équations de
. Les équations de
prochain état sont:
![]()
![]()
L’équation de sortie est
![]()
- Dessinez le schéma logique du circuit
- Déterminez le tableau d’états
- Dessinez le diagramme d’état
Réponse
- Schéma logique
- Tableau d’états
| État présent | État suivant | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 2 | 1 |
| 1 | 1 | 1 | 2 | 1 |
| 2 | 0 | 0 | 3 | 1 |
| 2 | 0 | 1 | 2 | 1 |
| 2 | 1 | 0 | 2 | 1 |
| 2 | 1 | 1 | 2 | 1 |
| 3 | 0 | 0 | 3 | 1 |
| 3 | 0 | 1 | 2 | 1 |
| 3 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 |
- Diagramme d’état
Question
Considérez le circuit logique suivant:
- Quelle est la fonction combinatoire réalisée par la section logique
combinatoire, c’est-à-dire, quelle est la fonction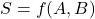 ?
? - Complétez le diagramme temporel de la figure, en supposant un temps
de propagation maximum de 10 ns pour les portes NOR et OU, et de
40 ns pour les bascules. - Si les temps de maintien
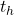 et de mise en place
et de mise en place 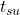 sont
sont
de 5 ns pour toutes les bascules, quelle est la fréquence maximale
d’horloge utilisable pour que le circuit fonctionne convenablement?
Utilisez un diagramme temporel pour évaluer la période minimum.
Réponse
- Fonction combinatoire
![Rendered by QuickLaTeX.com \[ S = A \oplus B \]](https://pressbooks.etsmtl.ca/app/uploads/quicklatex/quicklatex.com-bc25897b1ed81793e9ed75349b41e2c3_l3.png)
- Diagramme temporel
- Analyse pour la période minimale
La période minimale de l’horloge est de ![]() .
.
Question
Analysez le circuit logique suivant:
- Analysez le comportement du circuit, en supposant qu’au départ les
entrées sont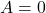 et
et 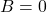 et la sortie
et la sortie 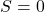 . Vous devez supposer
. Vous devez supposer
des changements des valeurs d’entrées et décrire les changements
des sorties, en tenant compte de la mémoire du circuit. - Identifiez la fonction des entrées
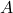 et
et 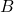 .
. - Identifiez la fonction du circuit.
Réponse
- Fonction
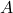 sert d’entrée de données,
sert d’entrée de données, 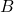 sert d’entrée de contrôle.
sert d’entrée de contrôle.- Le circuit se comporte comme un loquet D.
Question
Considérez circuit séquentiel décrit par le diagramme d’état suivant:
- En utilisant l’assignation d’états
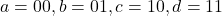 , construisez le tableau d’état pour ce circuit séquentiel.
, construisez le tableau d’état pour ce circuit séquentiel. - Concevez le circuit en utilisant des portes standards et des
bascules D.
Réponse
- Tableau d’état
État présent 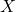
État suivant 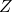
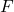
00 0 00 0 0 00 1 01 0 1 01 0 10 0 0 01 1 11 1 0 10 0 00 0 0 10 1 11 0 0 11 0 11 1 1 11 1 11 1 1 - Circuit
Question
Vous devez concevoir un circuit logique séquentiel à une entrée et une
sortie qui identifie les deux séquences d’entrée 0110 et 11111
appliquées immédiatement après une remise à zéro asynchrone du
circuit. Donnez le diagramme d’état simplifié pour ce circuit.
Réponse
Question
Vous devez concevoir un circuit logique séquentiel à une entrée et
une sortie qui identifie les deux séquences d’entrée 0110
et 11111. Les séquences d’entrée doivent être identifiées à
n’importe quel moment où elles apparaissent en entrée.
Réponse
Question
Déterminez le diagramme d’état pour un circuit séquentiel synchrone
avec une entrée ![]() et une sortie
et une sortie ![]() qui est utilisé pour
qui est utilisé pour
reconnaître la séquence d’entrée 101. La sortie doit donc être ![]()
lorsque le dernier 1 de la séquence 101 est identifié. ![]() est
est
ensuite remis à zéro au prochain coup d’horloge. Les chevauchements de
101 ne sont pas permis. Par exemple,
![]()
![]()
Réponse
Question
Concevez le circuit séquentiel synchrone décrit par le tableau d’état
ci-dessous. Vous devez considérer des bascules JK et D et choisir la
solution la plus simple. Présentez clairement toutes les étapes,
jusqu’au schéma du circuit correspondant.
| État courant | Entrée | Prochain | Sortie |
|---|---|---|---|
| 00 | 0 | 01 | 0 |
| 00 | 1 | 11 | 0 |
| 01 | 0 | 10 | 0 |
| 01 | 1 | 00 | 1 |
| 11 | 0 | 00 | 1 |
| 11 | 1 | 10 | 0 |
| 10 | 0 | 10 | 1 |
| 10 | 1 | 01 | 1 |
Réponse
Question
Les deux bascules du circuit suivant sont activées par les
transitions montantes du signal présent à leur entrée
d’horloge.
Tracez le chronogramme pour ![]()
Réponse
Question
Vous devez analyser le circuit séquentiel suivant:
- Donnez les équations pour le décodeur de prochain état.
- Donnez le tableau d’activation avec état présent, entrée, entrées
des bascules, prochain état, sortie. - Donnez le diagramme d’état correspondant.
- Tracez le chronogramme de fonctionnement, en faisant abstraction
des délais de propagation. - En sachant que la bascule a les caractéristiques suivantes:
- temps de pré-positionnement minimum: 11 ns
- temps de maintien minimum: 9 ns
- temps de propagation maximum: de Horloge à
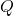 ou
ou
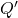 :
: 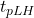 = 15 ns,
= 15 ns, 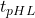 = 13 ns.
= 13 ns.
et en supposant un délai de propagation de 15 ns pour la porte
XOR, déterminez la période minimale et la fréquence
maximale qu’on puisse utiliser tout en étant assuré que le circuit
fonctionne correctement. Donnez les détails de votre raisonnement.
Réponse
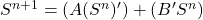
- Tableau d’activation
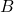
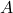
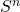
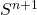
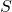
0 0 0 0 0 0 0 1 1 1 0 1 0 1 0 0 1 1 1 1 1 0 0 0 0 1 0 1 0 1 1 1 0 1 0 1 1 1 0 1 - Diagramme d’état
- Chronogramme
- Analyse temporelle
La période minimale est de
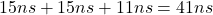 .
.
Question
Vous devez concevoir un circuit logique utilisé dans un système
permettant de trier des données. Le circuit reçoit deux nombres
non-signés de 4 bits, multiplexés en série sur une même entrée. Par
exemple, si les entrées sont ![]() et
et ![]() , le circuit recevra
, le circuit recevra ![]() .
.
Le circuit doit acheminer le plus grand des deux nombres à
une sortie (parallèle) appelée PG et le plus petit à une sortie
(parallèle) appelée PP. Vous devez réaliser votre circuit en utilisant
les éléments suivants:
- démultiplexeur un-vers-deux
- multiplexeur 4 bits deux-vers-un (il s’agit de quatre
multiplexeurs deux-vers-un à un bit avec le même signal de
commande, et qui traitent ainsi en parallèle des mots de quatre bits) - registre à décalage entrée série/sortie parallèle
- comparateur de magnitude: deux entrées parallèles de 4 bits:
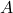 et
et
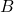 , trois sorties:
, trois sorties: 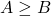 ,
, 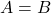 ,
, 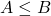
- registre entrée parallèle/sortie parallèle
Donnez un schéma-bloc de votre circuit en indiquant seulement les
blocs qui traitent les données (pas les blocs qui serviront à
contrôler le circuit).
Réponse

Question
On doit concevoir un système séquentiel avec une entrée ![]() et une
et une
sortie, et qui génère les séquences de sortie suivantes:
- si
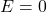 , séquence de sortie = 1100, périodique
, séquence de sortie = 1100, périodique - si
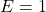 , séquence de sortie = 1011, périodique
, séquence de sortie = 1011, périodique
On envisage deux versions du système:
- version 1
- si
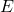 change, la séquence de sortie suit le
change, la séquence de sortie suit le
changement au vol. - version 2
- si
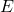 change, la séquence de sortie recommence à
change, la séquence de sortie recommence à
partir du début.
Par exemple,
| Entrée | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sortie version 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| Sortie version 2 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
Donnez un diagramme d’état pour chacune des deux versions.
Réponse
- Diagramme d’état, version 1
- Diagramme d’état, version 2
Question
Considérez le tableau d’état suivant:
| État présent | Entrée |
État suivant | Sortie |
|---|---|---|---|
| a | 0 | c | 1 |
| a | 1 | a | 1 |
| b | 0 | e | 0 |
| b | 1 | f | 1 |
| c | 0 | b | 1 |
| c | 1 | d | 0 |
| d | 0 | a | 0 |
| d | 1 | b | 1 |
| e | 0 | e | 0 |
| e | 1 | f | 1 |
| f | 0 | c | 1 |
| f | 1 | f | 1 |
correspondant à un circuit séquentiel synchrone.
- Simplifiez ce tableau d’état en identifiant les états
équivalents, en utilisant la méthode du tableau d’implication. - Donnez le diagramme d’état simplifié correspondant au tableau
d’état simplifié. Nommez les états simplifiés qui restent a,
b, c, … - Assignez des codes aux états, en commençant avec la
représentation binaire de 0 pour a, de 1 pour b, etc. - Donnez les diagrammes de Karnaugh pour le décodeur de prochain
état en supposant des bascules JK, et les fonctions simplifiées
correspondantes. - Donnez le diagramme de Karnaugh pour le décodeur de sortie.
- Dessinez le schéma du circuit séquentiel obtenu.
Réponse
- Tableau d’implication
| b | X | — | — | — | — | |
|---|---|---|---|---|---|---|
| c | X | X | — | — | — | |
| d | X | XX | X | — | — | |
| e | X | OUI | X | XX | — | |
| f | OUI | X | X | X | X | |
| a | b | c | d | e |
- Tableau d’état, assignation d’états et diagramme d’état
| État présent | Entrée |
État suivant | Sortie |
|---|---|---|---|
| a | 0 | c | 1 |
| a | 1 | a | 1 |
| b | 0 | b | 0 |
| b | 1 | a | 1 |
| c | 0 | b | 1 |
| c | 1 | d | 0 |
| d | 0 | a | 0 |
| d | 1 | b | 1 |
| État | Code |
|---|---|
| a | 00 |
| b | 01 |
| c | 10 |
| d | 11 |
- Diagrammes de Karnaugh, décodeur de prochain
état
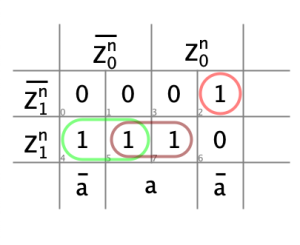
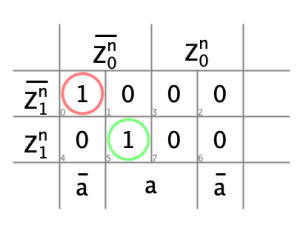
- Diagrammes de Karnaugh, décodeur de sortie
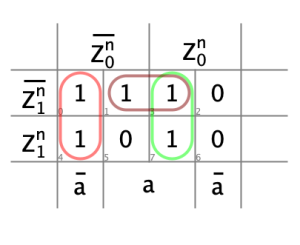
- Schéma du circuit
Question
Considérez le circuit séquentiel synchrone ci-dessous.
Déterminez la vitesse d’horloge maximale en considérant les
caractéristiques suivantes:
- Portes: temps de propagation maximum: 10 ns.
- Bascules: temps de mise en place minimum: 12 ns.
- Bascules: temps de maintien minimum: 15 ns.
- Bascules: temps de propagation maximum: de H à
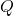 ou
ou
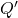 :
: 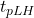 = 25 ns,
= 25 ns, 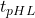 = 20 ns.
= 20 ns.
Réponse
La période minimale de l’horloge est de ![]() .
.
Série 5
Question
Faire le diagramme d’état d’un circuit séquentiel synchrone qui génère
à sa sortie un 1 lorsqu’il détecte à son entrée la séquence 0110 ou la
séquence 0101.
Réponse
Question
Un circuit séquentiel synchrone est construit à partir de trois
bascules, ![]() ,
, ![]() , et
, et ![]() . Il comporte une entrée
. Il comporte une entrée ![]() et
et
une sortie ![]() . Son diagramme d’état est donné ci-dessous.
. Son diagramme d’état est donné ci-dessous.
Vous devez concevoir ce circuit en considérant les états inutilisés
comme des cas facultatifs. Le circuit final doit être analysé pour
déterminer si, à partir des états inutilisés, le système revient vers
son fonctionnement normal.
- Conception avec des bascules D
- Conception avec des bascules JK
Réponse
- Conception avec des bascules D
- Conception avec des bascules JK
Question
Faire le diagramme d’état d’un compteur synchrone qui produit les
séquences d’états suivants, selon la valeur de l’entrée ![]()
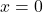 , séquence: 0, 6, 2, 1, 4, 0, 6, 2, 1, 4, …
, séquence: 0, 6, 2, 1, 4, 0, 6, 2, 1, 4, …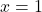 , séquence: 0, 6, 5, 7, 2, 1, 0, 6, 5, 7, 2, 1, …
, séquence: 0, 6, 5, 7, 2, 1, 0, 6, 5, 7, 2, 1, …

