Solutions chapitre 7
| Question 1 | Question 2 |
| Question 4 |
Question 1
Dans l’exemple de la nouvelle cimenterie, dans la section 7.3.1, vérifiez que l’approche par partie permet d’obtenir également une VAN = 160 millions de dollars. Distinguez les parties prenantes suivantes : les consommateurs, les producteurs déjà établis et la nouvelle usine.
Réponse
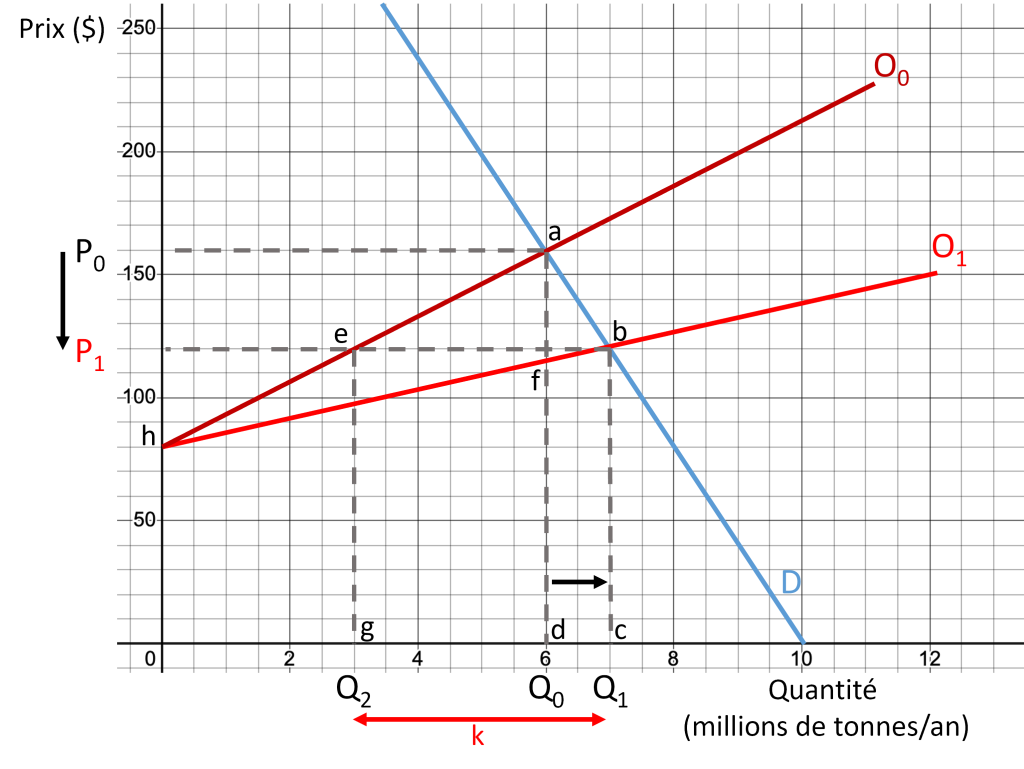
| Partie | Impact | Valeur |
| Consommateurs | Baisse du prix de 160 $ à 120 $, ce qui augmente le SC (P0abP1). | 260 millions $ |
| Producteurs préexistants | Baisse de leur SP (P0aeP1) | -180 millions $ |
| Nouvelle usine |
Surplus = Profits = Ventes – Coûts (Tous les coûts sont évitables.) (Non visible sur le graphique.) |
120 $ x 4 m – 400 millions $ = 80 millions $ |
| VAN | 160 millions $ |
Question 2
Une ligne de train de banlieue transporte en moyenne 75 000 usagers par année entre la banlieue et le centre-ville. Le prix de 15 $ par trajet couvre le coût moyen d’exploitation. Un projet vise à améliorer les voix, de sorte que la durée du trajet diminue de 45 minutes à 25 minutes. On estime que la valeur moyenne du temps des usagers du train est de 7 $/heure. De plus, on estime que l’élasticité de la demande par rapport au prix (ou au coût) généralisé est de 0,7. Le projet augmentera le coût moyen d’exploitation de 10 %, mais le prix du trajet ne sera pas modifié. En supposant une demande linéaire, déterminez la valeur de l’impact sur les usagers.
Réponse
La valeur de l’impact sur les usagers est d’environ 182 597 $, comme nous le montrons ci-dessous.
Le prix généralisé initial : 15 $ + 7 $ x (45/60) = 20,25 $
Nouveau prix généralisé : 15 $ + 7 $ x (25/60) = 17,91$
Soit une baisse de 11,55 %[1], ce qui devrait se traduire par une hausse du trafic de 8,08 %[2], de sorte que l’achalandage devrait être d’environ 81 066 déplacements (1,0808 x 5 000).
L’impact sur les utilisateurs se mesure par le changement du surplus, qu’on peut calculer comme suit :
Variation du surplus = (baisse du prix généralisé x le trafic existant) + (½ x baisse du prix généralisé x trafic induit) = (2,34 $ x 75 000) + (½ x 2,34 $ x 6066) = 182 597 $.
Question 4
Un musée des beaux-arts envisage d’accueillir une exposition de calibre international des œuvres d’Alberto Giacometti. L’exposition coûtera 1 million de dollars pour un événement de 4 mois. En considérant les résultats de cette exposition dans d’autres musées où elle a été présentée, on estime qu’elle devrait attirer 120 000 visiteurs de plus que le nombre de visiteurs anticipés s’il n’y avait que les expositions permanentes du musée. Les recettes additionnelles prévues (billetteries, stationnement et boutiques) sont évaluées à 1,2 million de dollars. Les coûts d’opération devraient cependant augmenter de 350 000 $. Quel devrait être le surplus d’un visiteur moyen pour que cette exposition se justifie par les bénéfices directs aux usagers ? Étant donné la courte durée de ce projet, il n’est pas utile d’actualiser.
Réponse
Il y a deux parties : les visiteurs et le musée. Le Tableau ci-dessous résume l’ACA avec l’approche par partie.
| Partie | |
| Usage | Surplus du consommateur inconnu: on doit établir le seuil de rentabilité X $ |
| Musée |
Profit d’opération = 1,2 m $ – 0,35 m $ = + 0,85 m $ Coût fixe de l’exposition : – 1 m $ |
| VAN | = 0 $ (seuil de rentabilité) |
Il faut donc que le SC soit d’au moins 0,15 million $ pour que la VAN = 0. Cela correspond à un SC moyen par visiteur de 1,25 $, ce qui semble raisonnable.

