Solutions chapitre 10

Question 1

(*) Dans un pays, la production de café se répartit entre un grand nombre de petits producteurs. Les récoltes sont cependant achetées par un seul acheteur autorisé par le gouvernement. Un projet est envisagé pour libéraliser ce marché, ce qui se traduirait par une augmentation importante du nombre d’acheteurs.

Pour évaluer les impacts potentiels de ce projet sur le marché du café, vous disposez des données suivantes :

• Le prix actuel sur le marché s’élève à 2000 $ la tonne;
• La quantité échangée monte à 10 millions de tonnes;
• L’élasticité-prix de l’offre est estimée à 2, et celle de la demande à 1.

Établissez un cadre d’analyse permettant d’identifier et de valoriser les impacts du projet sur le marché du café. Discutez comment les élasticités déterminent l’effet net dans le marché. Analysez également les autres effets qu’il faudrait prendre éventuellement en compte dans une ACA complète de ce projet.

[La résolution s’effectue à partir des notions développées dans l’Annexe 2.]

Résolution

La Figure 13 illustre le cadre d’analyse de ce projet.

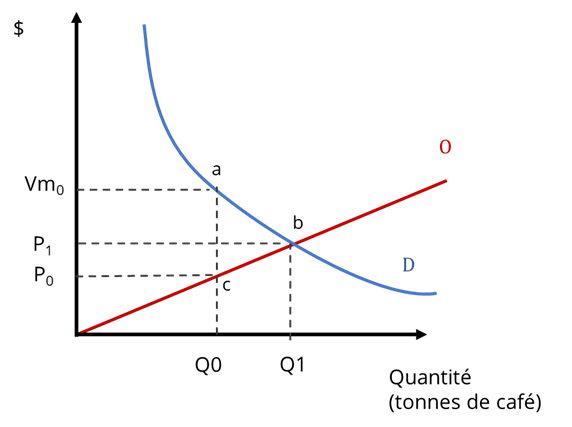
Scénario de référence (monopsone) :

Q0 = 10 millions de tonnes

P₀ = 2000 $ la tonne

Scénario avec libéralisation :

Dans le meilleur des cas, le marché devient parfaitement concurrentiel. Il faut donc déterminer quels seront la quantité (Q1) et le prix (P₁) dans un contexte concurrentiel.

L’effet net qu’on vise à évaluer est la perte sèche abc entraînée par le monopsone. Pour cela, nous devons aussi évaluer Vm0, soit la valeur marginale du monopsone.

Comme l’annexe 2 l’illustre, le monopsone maximise son surplus lorsque :

[latex]L = \frac{Vm_0 - P_0}{Vm_0} = \frac{1}{\eta_O}[/latex]

Avec P₀ = 2000 $ et [latex]\eta_O = 2[/latex], nous pouvons déduire que [latex]Vm_0[/latex] = 4 000 $. Il s’avère ensuite possible d’estimer P₁, le prix en concurrence parfaite, en utilisant les formules d’incidence d’une taxe, puisque nous nous trouvons dans un contexte semblable, où un écart existe entre le prix de la demande et le prix de l’offre (voir le chapitre 8 section 1.2).  Ainsi, le pourcentage de l’écart de 2 000 $ qui réduit le prix pour les producteurs relativement au prix concurrentiel est évalué à 1/3, à partir de l’application de la formule suivante [latex]\frac{\eta_D}{\eta_D + \eta_O} \%[/latex].

Ainsi, P₁ = 2000 $ + 1/3 x 2000 $ = 2 666 $, ce qui représente une hausse de 33 % du prix, signifiant que la quantité produite devrait être 66 % plus élevée en concurrence parfaite, puisque l’élasticité de l’offre est de 2.  On prévoit donc que Q1 = 16,6 millions de dollars. Ainsi, la perte sèche évitée grâce au projet s’évalue approximativement à 6,6 milliards de dollars, soit ½ x 2000 $ x 6,6 millions de dollars.

Question 2

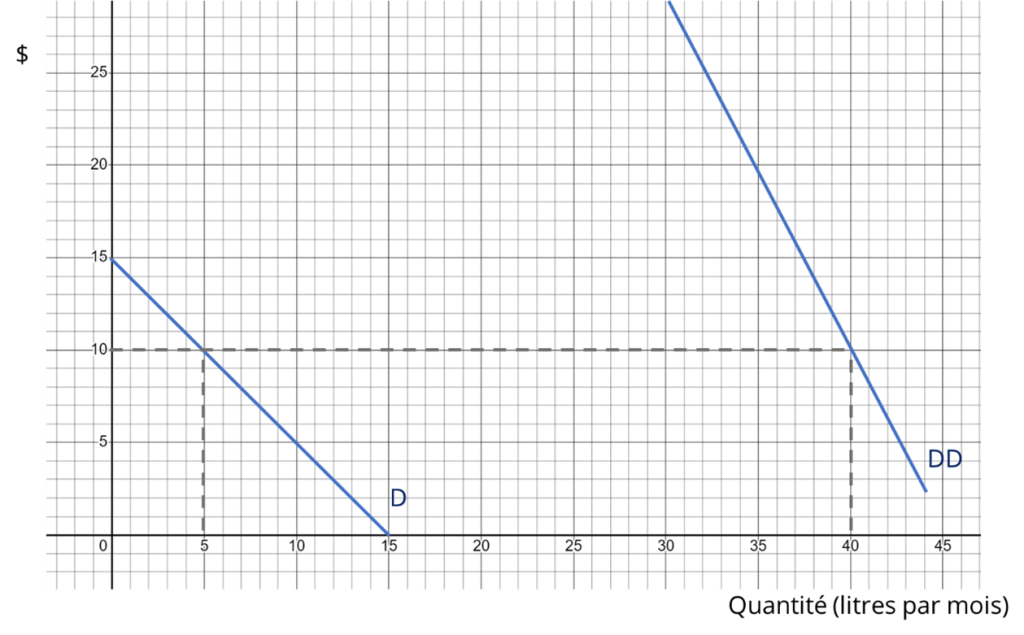
Un projet vise à lutter contre la dépendance à l’alcool. La demande type d’une personne dépendante est représentée à la Figure 8 par la courbe DD. La demande type pour une personne qui n’éprouve pas de dépendance est figurée par la courbe D. Le prix moyen de l’alcool est de 10 $ le litre. Discutez des enjeux liés à la valorisation des effets du projet du point de vue de la dépense et du surplus du consommateur

Résolution

Si le programme permet de combattre la dépendance à l’alcool chez une personne, l’un de ses avantages provient de la réduction de ses dépenses mensuelles liées à l’alcool, passant de 400 $ à 50 $ (en supposant une consommation conforme à la moyenne d’une personne non dépendante). Toutefois, il est important de prendre en considération la diminution de l’avantage associé à la consommation d’alcool, représenté par l’aire située sous la courbe de la demande entre 40 litres et 5 litres. En utilisant la courbe de demande DD, la réduction de la consommation entraîne une perte de bien-être importante pour la personne. Cependant, cette approche présente un inconvénient, puisque la dépendance à l’alcool influence la courbe DD. On peut donc soutenir que la courbe DD ne capte pas de manière adéquate l’avantage associé à la consommation d’alcool pour cette personne.

Une alternative consiste à utiliser la courbe de la demande D pour évaluer la perte d’avantages résultant de la réduction de la consommation. Ainsi, une diminution de la quantité consommée de 40 litres à 5 litres entraînerait une réduction des avantages correspondant à l’aire du triangle abc, soit 50 $ par mois. Par conséquent, l’effet net deviendrait positif, avec un gain net de 300 $ par mois.

Il est également important de prendre en compte les coûts externes évités grâce à la réduction de la consommation d’alcool, tels que la diminution des dépenses de soins de santé.