La valorisation des extrants en l’absence de distorsion

Philippe Barla

7 La valorisation des extrants en l’absence de distorsion

Motivation et objectifs d’apprentissage

Source: Pline, CC BY-SA 3.0 via Wikimedia Common

La ville d’Hamilton, Ontario, a décidé de remplacer sa ligne d’autobus express reliant l’Université McMaster à Eastgate Square par un système léger sur rail (SLR) plus moderne et efficace. Cette nouvelle ligne s’étendra sur une distance de 14 km et comportera 17 arrêts. Les principaux avantages du SLR sont :

Une vitesse de déplacement supérieure (34 km/h au lieu de 21 km/h) permettant des déplacements plus rapides ;
Une capacité accrue, afin de répondre à la forte croissance anticipée de la population ;
Un service plus confortable et ponctuel.

Quel cadre d’analyse utiliser pour valoriser ces extrants dans une ACA ?

Dans ce chapitre, nous utilisons les outils étudiés précédemment pour construire le cadre d’analyse de projets qui contribuent directement à l’offre d’un bien ou d’un service. Nous nous concentrons sur la valorisation d’extrants dans des marchés primaires, en mettant de côté pour l’instant l’influence de distorsions et les enjeux liés à la valorisation des intrants. Étant donné la diversité des contextes, nous examinons des situations types qui permettent de créer les réflexes nécessaires pour analyser d’autres situations.

À la fin de ce chapitre, vous serez en mesure de concevoir un cadre d’analyse pour un projet qui :

Introduit un nouveau bien ou service ;
Améliore la qualité d’un bien ou d’un service existant ;
Augmente l’offre dans un marché concurrentiel.

7.1 Le projet offre un nouveau service

Plusieurs projets soumis à une ACA consistent à construire une infrastructure qui permet aux usagers de profiter d’un nouveau service. Il peut s’agir, par exemple, de la construction d’un pont, d’un musée, d’une salle de spectacle ou d’une infrastructure sportive. Chaque projet a ses spécificités, mais ces initiatives partagent souvent des caractéristiques communes par rapport aux coûts et aux avantages, comme le met en évidence le Figure 7.1.

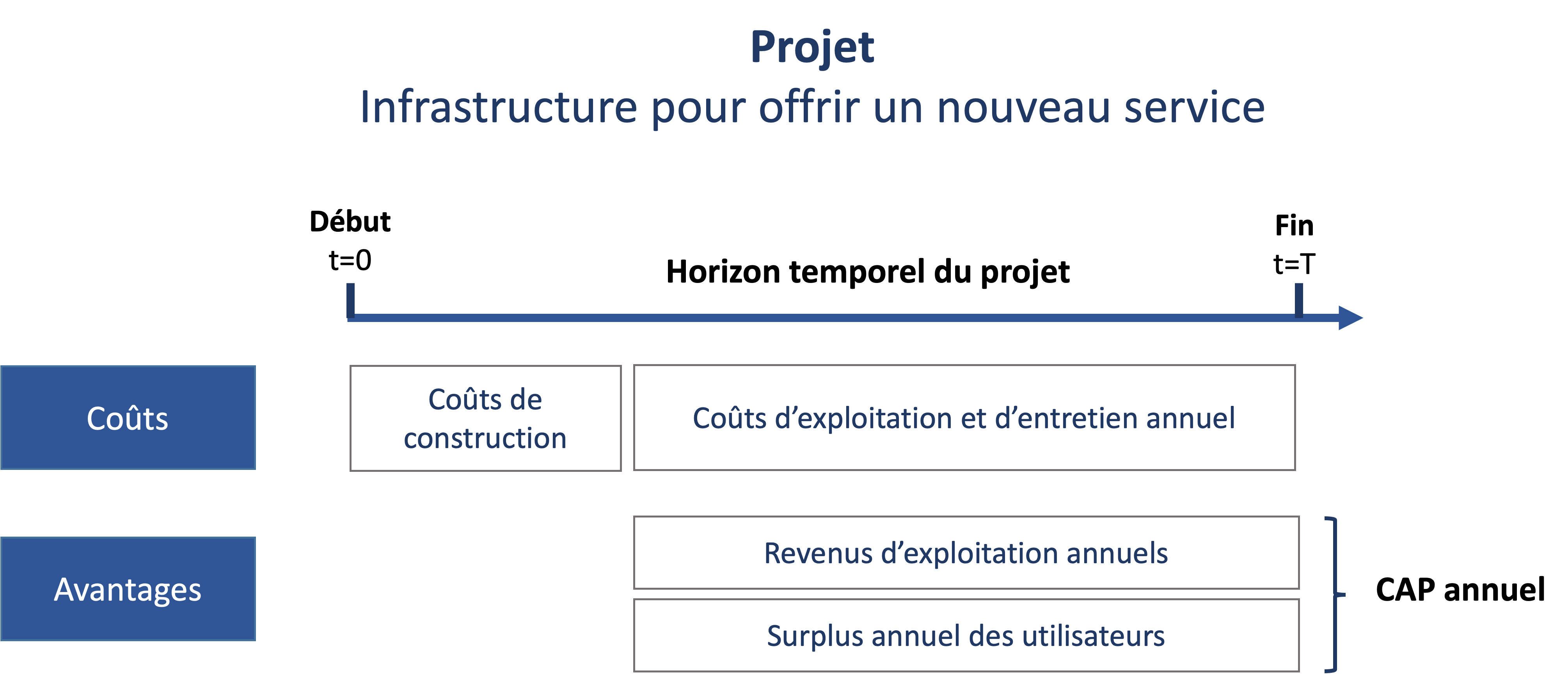
*Figure 7.1 Les impacts d’une nouvelle infrastructure*

Les coûts

Les coûts liés à la construction de l’infrastructure constituent généralement l’un des éléments majeurs du coût total. Ces dépenses, qui sont engagées principalement au début du projet, se transforment en coûts fixes inévitables une fois l’infrastructure rendue opérationnelle.

L’autre volet des coûts concerne les coûts d’exploitation et de maintenance. Ces dépenses varient souvent très peu en fonction du nombre d’usagers. Qu’il s’agisse d’une salle de spectacle comble ou presque vide, les coûts d’exploitation d’un théâtre varient assez peu. Une augmentation du personnel à l’accueil peut s’avérer nécessaire lors des jours d’affluence, mais les coûts liés au bâtiment, à l’assurance et aux artistes demeurent constants. De plus, ces dépenses peuvent généralement être évitées si l’infrastructure est fermée. Par conséquent, les coûts opérationnels sont de nature quasi-fixe.

Ainsi, les coûts dans ce type de projet se caractérisent habituellement comme suit :

Prédominance des coûts fixes et quasi-fixes ;
Coût marginal d’un usager supplémentaire très faible, voire négligeable ;
Diminution du coût moyen par usager à mesure que le taux d’utilisation de l’infrastructure augmente (effet d’économie d’échelle).

Les avantages

Comme nous l’avons vu au chapitre 4, l’avantage brut des utilisateurs du nouveau service se mesure par le consentement à payer (CAP), soit l’aire sous la courbe de la demande entre zéro et la quantité échangée. De plus, le CAP se répartit entre les différentes parties prenantes : les utilisateurs conservent le surplus du consommateur (SC), l’opérateur de l’infrastructure s’approprie les recettes d’opération^[1]. Celles-ci servent notamment à couvrir en tout ou en partie les coûts d’exploitation et les coûts de l’infrastructure.

L’importance relative des revenus d’opération et du SC dépend du type de tarification utilisée. Si l’accès est gratuit pour les usagers, le SC correspond au CAP, et les revenus d’exploitations sont nuls. Avec un prix positif, l’opérateur s’approprie une partie du CAP. Nous reviendrons sur l’impact de la tarification au chapitre 10.

En pratique, la principale difficulté réside dans l’évaluation de la demande pour le nouveau service. Cette évaluation peut être réalisée en utilisant des méthodes qualitatives telles qu’une étude de marché ou la méthode Delphi, ou des méthodes quantitatives comme l’analyse de séries chronologiques et d’autres techniques économétriques. L’analyse de ces approches dépasse le cadre de ce manuel (Bourbonnais et Usunier, 2017). Toutefois, certaines des techniques qui seront discutées dans la partie 3 pourraient être utiles pour estimer la demande pour un nouveau service.

L’exercice ci-dessous permet de mettre en pratique les éléments étudiés dans cette section et dans les chapitres précédents.

Exercice : Un parc d’attractions aquatiques

Une ville isolée envisage de subventionner la construction d’un parc d’attractions aquatiques. Le coût est évalué à 3 millions de dollars, et l’édification devrait durer un an. La municipalité investirait 1 million de dollars, et le reste proviendrait d’un investisseur local privé qui serait responsable des opérations. Selon le plan d’affaires du projet, le prix d’entrée s’élèverait à 15 $, et le nombre d’admissions serait de 20 000 par an. Les coûts d’exploitation annuels sont estimés à 100 000 $. Une fois en opération, le parc aura une durée de vie utile de 20 ans. Effectuez une ACA de ce projet, en utilisant un taux d’actualisation de 5 %.

Solution

Appliquons les deux premières étapes de la démarche proposée dans le chapitre 2, afin d’évaluer la rentabilité sociale d’un projet.

Étape 1 : Le contexte, le projet et l’état des connaissances

Comme il s’agit d’un exemple fictif, il y a peu à dire sur le contexte, sauf en ce qui concerne les arguments économiques qui peuvent justifier un investissement de la ville. Cette infrastructure contribuera à favoriser l’exercice physique des résidents comme dans l’exemple de la piscine du chapitre 4^[2]. Une revue des connaissances pourrait aider à mieux documenter cet impact et à évaluer plus précisément la demande pour ce type d’infrastructure.

Les scénarios à l’étude sont :

Le scénario de référence : absence du parc ;
Le scénario avec projet : construction du parc d’attractions aquatiques.

L’horizon temporel est de 21 ans, comprenant une année pour la construction, et l’horizon spatial est considéré comme universel.

Étape 2 : Le cadre d’analyse

Pour établir le cadre d’analyse, il est utile d’identifier le marché de l’extrant qui est directement affecté par le projet (marché primaire d’extrants). En nous appuyant sur le système de classification des industries de l’Amérique du Nord (SCIAN), un parc d’attractions aquatiques fait partie de la classe 71311 Parcs d’attractions et jardins thématiques dans le secteur 71 – Arts, spectacles et loisirs. Pour notre analyse, le marché analysé peut encore être plus précis, soit le marché des parcs d’attractions aquatiques. Ce service est suffisamment différencié pour qu’il puisse être considéré comme un marché spécifique. Par ailleurs, comme la ville est isolée, il n’est pas nécessaire de soucier de l’existence éventuelle de parcs concurrents dans des villes voisines. La présence d’autres activités récréatives dans la ville (par exemple, plaine de jeux ou salle de cinéma) déterminera l’importance de la demande pour le parc et son élasticité-prix.

Concernant la nature du service offert, l’amusement aquatique constitue un service marchand pour lequel l’excluabilité est peu coûteuse. Le service n’engendre pas de rivalité de consommation, sauf si le parc devient congestionné (bien club congestible).

Les parties prenantes sont les usagers, l’investisseur privé et la municipalité. Les autres services récréatifs de la ville pourraient voir leur demande diminuer avec l’ouverture du parc, mais il s’agit d’effets indirects que nous ne considérerons pas à ce stade (voir le chapitre 12).

Nous pouvons maintenant établir le cadre d’analyse, afin d’identifier les effets primaires. Du côté de la demande, nous disposons d’un point, soit (Q = 20 000, p = 15 $). Bien entendu, l’analyste devra évaluer le bien-fondé de cette estimation, en la comparant avec les données de parcs comparables ou en effectuant une étude de marché indépendante. La Figure 7.2 illustre la demande pour le parc. Sa représentation est imprécise, puisque nous ne disposons que d’un seul point.

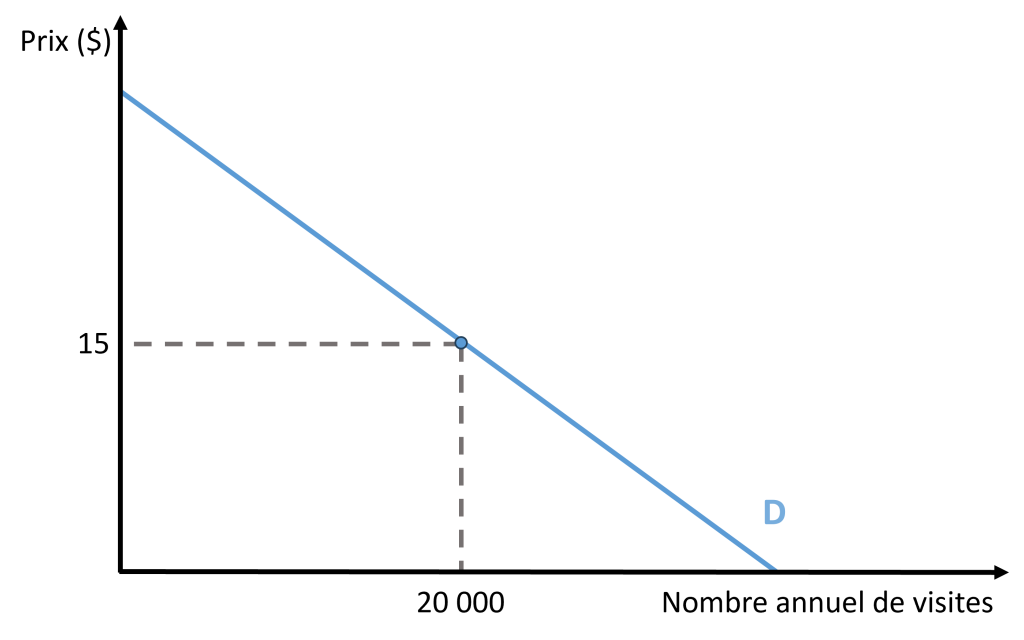
*Figure 7.2 Demande pour le parc d’attractions*

Du côté de l’offre, il n’y a qu’une seule entreprise, de sorte que nous ne nous trouvons pas dans un contexte de concurrence pure et parfaite, où la courbe de l’offre se confond avec le coût marginal. Comme nous le verrons au chapitre 10, il n’existe pas de courbe d’offre dans un contexte de monopole. Nous disposons cependant d’informations sur la structure des coûts et sur la tarification envisagée. La structure des coûts comprend un coût fixe important pour la construction de l’infrastructure et des coûts d’exploitation annuels.

S’il n’est pas possible d’identifier la courbe de l’offre, on peut cependant illustrer graphiquement la situation du propriétaire. En effet, nous savons qu’il anticipe 20 000 visites annuelles lorsque le tarif s’élève à 15 $. Nous pouvons donc déterminer ses revenus et ses coûts moyens d’exploitation. Les revenus d’exploitation s’élèvent à 15 $ x 20 000 et correspondent à l’aire de la surface abcd sur la Figure 7.3. Les coûts d’exploitation peuvent aussi être représentés dans la Figure, puisque le coût d’exploitation moyen est de 5 $ (100 000 $ divisé par 20 000 visites). L’aire de la surface efdc représente donc les coûts d’exploitation^[3].

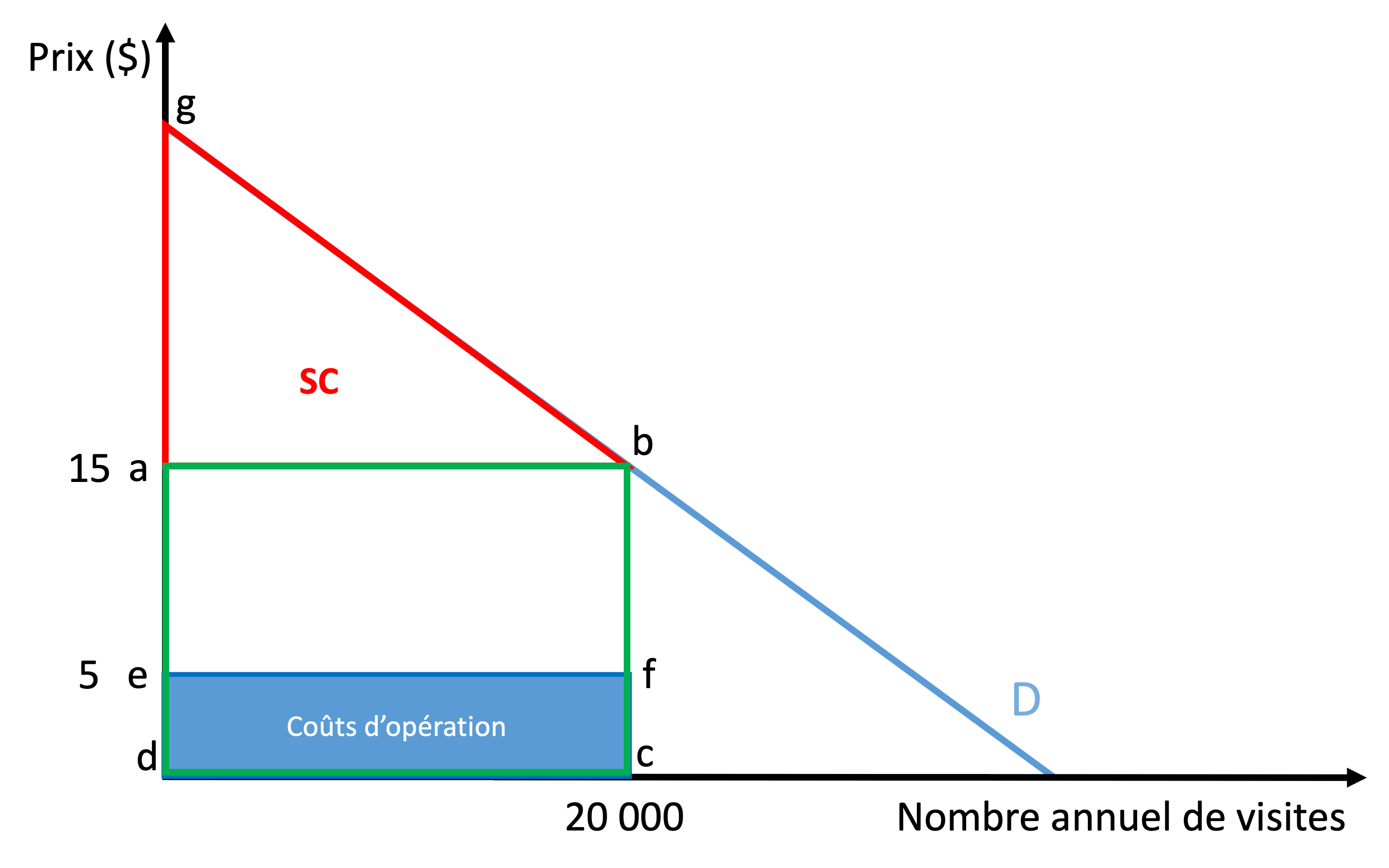
*Figure 7.3 Impacts de la construction d’un parc d’attractions*

À partir de la Figure 7.3, il est possible d’identifier les impacts appropriés en utilisant l’approche sociale ou l’approche par partie.

L’approche sociale

Le projet permet d’accroître la quantité de Q = 0 à Q = 20 000 entrées par an.

La valeur sociale de l’extrant du projet se mesure par le CAP, soit la surface sous la courbe de la demande entre Q = 0 et Q = 20 000, c’est-à-dire la surface gbcd.
La valeur sociale des ressources mobilisées se mesure par le coût de construction et les coûts annuels d’opération (la surface efcd).

Il n’y a pas de ressources épargnées par ce projet.

L’approche par partie

Conceptuellement, le projet correspond à une baisse du prix d’un niveau supérieur ou égal au prix de réserve, jusqu’au tarif prévu de 15 $.

L’impact pour les utilisateurs se mesure par le surplus du consommateur, soit la surface gba. Cet avantage peut être considéré comme une annuité perçue tout au long de l’année, à partir de la deuxième année du projet. Sur base des données disponibles, le SC ne peut cependant être évalué. Il faudrait en effet connaître le prix de réserve ou obtenir des informations sur l’élasticité-prix de la demande.

L’impact pour l’opérateur se mesure par le surplus du producteur, qui peut s’évaluer par le profit d’exploitation de 200 000 $ par année, soit la surface abef. Ce montant correspond à une annuité perçue au cours de chaque année, à partir de la deuxième année du projet. L’analyste devra cependant s’assurer que les coûts d’exploitation soient évalués adéquatement, en utilisant la notion de coût économique (ou coût de renonciation) et non sur la base uniquement des dépenses. Par exemple, le coût d’exploitation comprend-il une rémunération pour le temps que le propriétaire consacre au fonctionnement du parc ?

L’impact pour la municipalité se mesure par la baisse de son surplus lié à l’investissement d’un million de dollars^[4].

Le seuil de rentabilité

Sans information additionnelle pour estimer le SC, il est malgré tout possible de déterminer un seuil de rentabilité. Le Tableau 7.1 affiche les valeurs actualisées des impacts pour le propriétaire et pour la municipalité. Pour que la VAN du projet soit égale à zéro, il faut que la valeur actualisée du SC vaille au moins X = 543 520 $, soit la valeur nette de l’impact sur les deux autres parties. L’annualisation de cet avantage indique que le SC annuel doit être d’au moins x = 44 690 $ à partir de la deuxième période. Rapporté au nombre d’utilisateurs, cela signifie un surplus moyen par utilisateur d’au moins 2,25 $. Cette borne permet de savoir facilement si le projet est prometteur ou non : est-il réaliste que l’utilisateur moyen soit prêt à payer 2,24 $ de plus, soit 17,24 $, pour profiter du parc d’attractions ?

**Tableau 7.1 ACA par partie**
Partie	Avantage	Coût	Valeur actualisée
Utilisateurs	SC = x $/an (de t = 1,5 à t = 20,5)		X $
Investisseur privé	Profit opérationnel = 200 000 $ (de t = 1,5 à t = 20,5)	Investissement 2m (t = 0,5)	432 380 $
Municipalité		Investissement 1m (t = 0,5)
		Bornage – VAN = 0 $

Notes concernant le Tableau 7.1: rappelons que la première période correspond à la phase de construction. Comme les coûts de construction s’accumulent de façon continue durant la première période, l’actualisation doit s’effectuer avec t = 0,5 (voir le chapitre 6). Les opérations du centre commencent à la deuxième période et dureront pendant vingt ans, de sorte que la dernière période correspond à la 21^e période. Les avantages et les coûts sont des annuités qui s’accumulent pendant 20 ans. Comme les effets se produisent en cours de période, l’actualisation de ces annuités se réalise avec le facteur d’annuité [latex]a_{s = 5\%}^{T = 20} \times (1 + i)^{0.5} = 12,77[/latex]. Ensuite, il faut encore multiplier le facteur par [latex]1/\left(1+s\right)[/latex], puisque les effets ne commencent qu’à la deuxième période. Cela permet de ramener la valeur actualisée des annuités de t = 1 à t = 0.

7.2 Le projet améliore la qualité d’un service

Certains projets visent à améliorer la qualité d’un service existant, par exemple, le remplacement d’autobus pour améliorer le confort des usagers ou l’installation d’un système de chauffage dans une piscine publique. Dans le domaine des transports, l’amélioration prend souvent la forme d’une réduction du temps de déplacement au moyen de l’augmentation de la vitesse ou de la fréquence du service. Nous explorerons ces deux situations à partir d’exemples simples.

7.2.1 Amélioration de la qualité d’un service

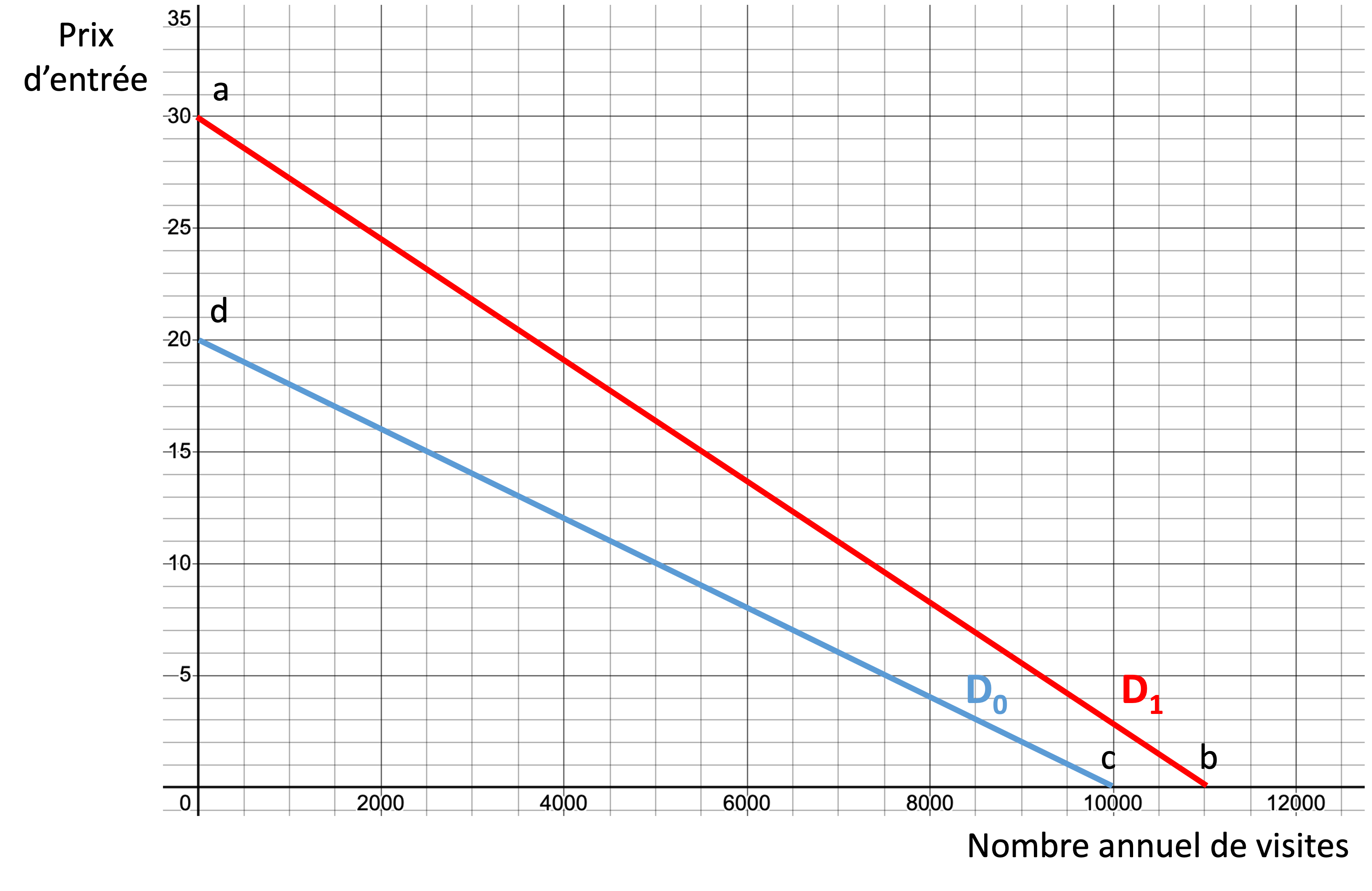
D’une manière générale, l’amélioration du service a pour conséquence d’accroître le consentement à payer des usagers, ce qui se traduit par un déplacement vers le haut de la courbe de la demande. En guise d’illustration, considérons un projet visant à installer un système de chauffage de l’eau dans une piscine municipale extérieure. La Figure 7.4 illustre la demande actuelle, sans chauffage, D₀. Sur la base d’une enquête auprès de la population et de l’analyse de projets comparables, on estime que la demande augmenterait à D₁ si l’eau était chauffée. En supposant un accès libre (le prix d’entrée est nul), l’impact du projet pour les utilisateurs se mesurerait par le changement dans le CAP. Dans le scénario de référence, le CAP s’élève à 100 000 $/an, alors que dans le scénario avec le projet, le CAP s’évaluerait à 165 000 $/an. Le projet générerait donc un avantage pour les usagers de 65 000 $/an soit l’aire de la surface abcd.

*Figure 7.4 Impact sur la demande du projet de chauffage d’une piscine*

7.2.2 La réduction du temps de déplacement

Un deuxième exemple permet d’illustrer la conception d’un cadre d’analyse pour des projets en transport qui modifient les temps de déplacement, une composition importante de la qualité du service dans ce domaine.

Le projet : Une ligne de train de banlieue transporte en moyenne 100 000 usagers par an entre la banlieue et le centre-ville. Le prix est de 15 $ par trajet, ce qui couvre le coût moyen d’exploitation. Un projet a pour objectif d’améliorer les voix, de sorte à réduire la durée du trajet de 45 minutes à 30 minutes. On estime que ce changement devrait augmenter l’achalandage de 20 %, avec un prix constant à 15 $. En supposant les hypothèses suivantes :

Il n’y a pas d’autres impacts ;
Les travaux dureront un an et ne perturberont pas le service actuel ;
La durée de vie de l’amélioration est de 20 ans (excluant l’année des travaux), et le taux d’actualisation sociale est de 3 % ;
Les coûts d’exploitation moyens restent à 15 $ ;
Les usagers sont prêts à payer en moyenne 10 $ pour économiser une heure de déplacement.

Déterminez la valeur actualisée des coûts du projet tel que la VAN = 0 $.

Résolution

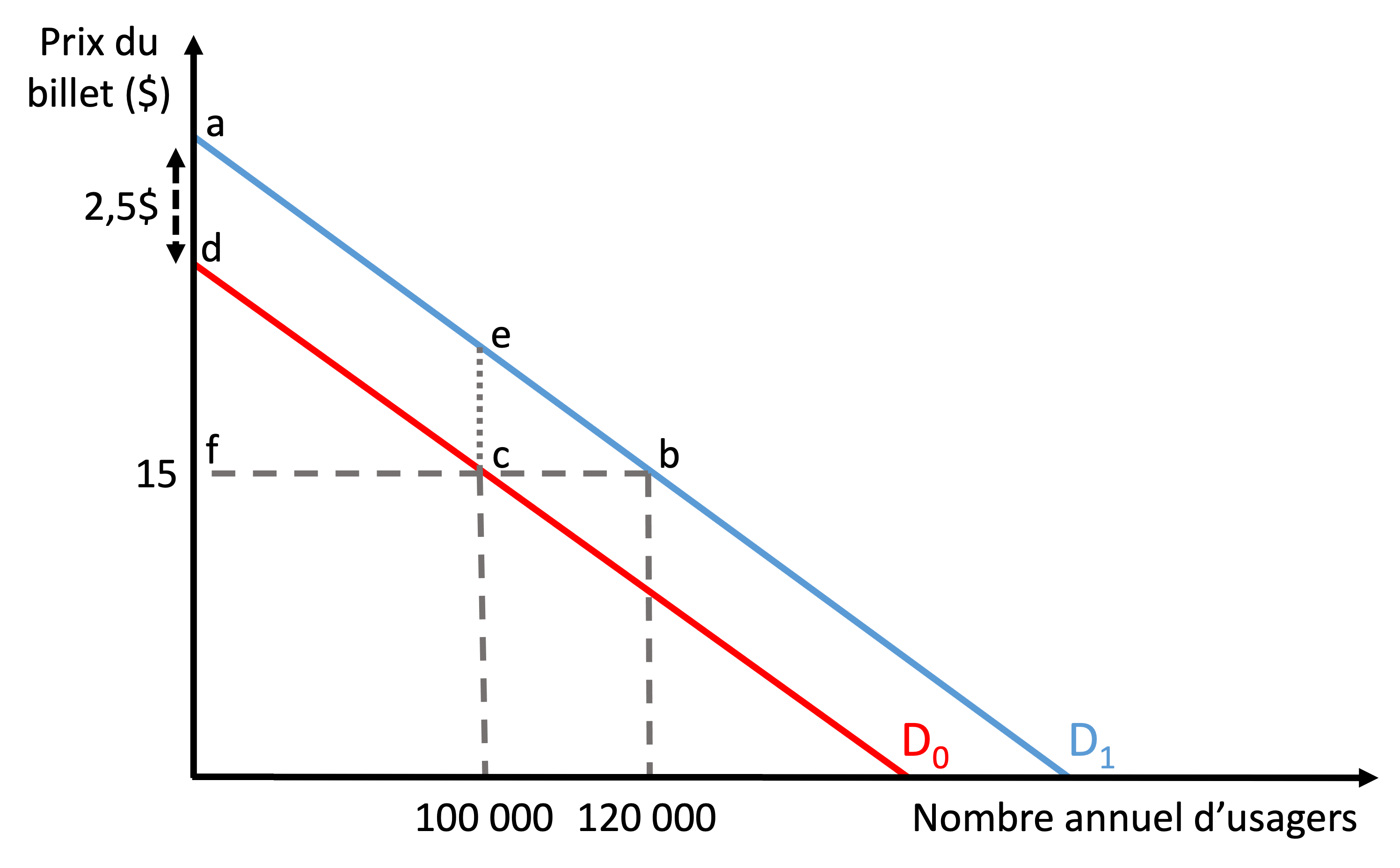
Le projet améliore la qualité du service, ce qui entraîne une hausse de la demande, comme dans l’exemple de la piscine chauffée. La Figure 7.5 illustre la demande actuelle (D₀), qui est imprécise, étant donné qu’on ne connaît qu’un seul point. Avec le projet, la qualité du service s’améliore, ce qui provoque un déplacement de la demande vers le haut (D₁). Le nombre d’usagers s’accroît de 20 %, lorsque le prix se maintient à 15 $.

Il est possible de déterminer plus précisément l’ampleur du déplacement de la courbe de la demande, grâce au concept de valeur du temps, abondamment utilisé dans le domaine des transports. Le chapitre 16 décrit plus en détail ce concept, mais à ce stade, définissons le paramètre ν comme la valeur du temps exprimée en $/heure. Cette valeur s’interprète comme le consentement à payer en moyenne pour économiser une heure de déplacement. Dans notre exemple, nous avons ν = 10$, de sorte que le consentement à payer pour le gain de temps généré par le projet est de 2,5 $, soit ν x (15/60). Les usagers seraient donc prêts à payer en moyenne 2,5 $ de plus pour un service plus rapide, ce qui se traduirait par un déplacement parallèle vers le haut de 2,5 $ de la demande. Évidemment, il s’agit probablement d’une simplification, puisqu’il est probable que le consentement à payer pour le gain de temps ne soit pas le même chez tous les usagers.

*Figure 7.5 Impact de la demande du projet de transport*

Il est maintenant possible de calculer l’avantage pour les usagers, en distinguant les personnes qui utilisaient déjà le train de banlieue des nouveaux usagers, soit le trafic induit par le projet. Pour les usagers courants, le surplus s’accroît de 2,5 $ par usager, ce qui représente un avantage de 250 000 $, soit la surface aecd. Pour les usagers attirés par le projet, le surplus moyen additionnel s’élève à ½ x 2,5 $, ce qui crée un surplus additionnel de 25 000 $, soit la surface ebc. Le Tableau 7.2 montre les résultats de cette ACA et permet de déterminer un seuil de rentabilité. En fait, si le projet coûte moins de 4 031 500 $, il sera socialement rentable^[5].

**Tableau 7.2 Seuil de rentabilité du projet de transport**
Partie	Avantage	Coût	Valeur actualisée
Usagers courants	250 000 $ (t = 1,5 @ t = 21,5)		3 665 000 $
Nouveaux usagers (Trafic induit)	25 000 $ (t = 1,5 @ t = 21,5)		366 500 $
Promoteur		Coût des travaux	-X $
		VAN =	0 $
Note : Le facteur d’annuité est de 14,66, en supposant que les avantages soient perçus au cours de chaque année.

Alternativement, il est possible de travailler avec la notion de coût ou de prix généralisé, qui intègre directement la valeur du temps. En effet, les décisions relatives au transport, incluant la sélection du mode de transport, des itinéraires, et la fréquence des déplacements, sont influencées par le prix généralisé [latex]\left( p_g \right)[/latex]. Ce dernier se définit de la manière suivante :

[latex]p_g = c + v \times t[/latex]

Avec :

[latex]c[/latex] : les coûts monétaires engendrés par la décision de transport (par exemple, les prix du billet, du stationnement et de l’essence) ;

[latex]v[/latex] : la valeur du temps exprimée en $/heure ;

[latex]t[/latex] : le temps de déplacement exprimé en heures.

Dans notre exemple, nous avons:

Avant le projet : [latex]p_g = 15\$ + 10\$ \times \frac{3}{4} = 22,5\$[/latex];

Après le projet : [latex]p_g^P = 15\$ + 10\$ \times \frac{1}{2} = 20\$[/latex].

Le projet entraîne donc une réduction du prix généralisé de 2,5 $.

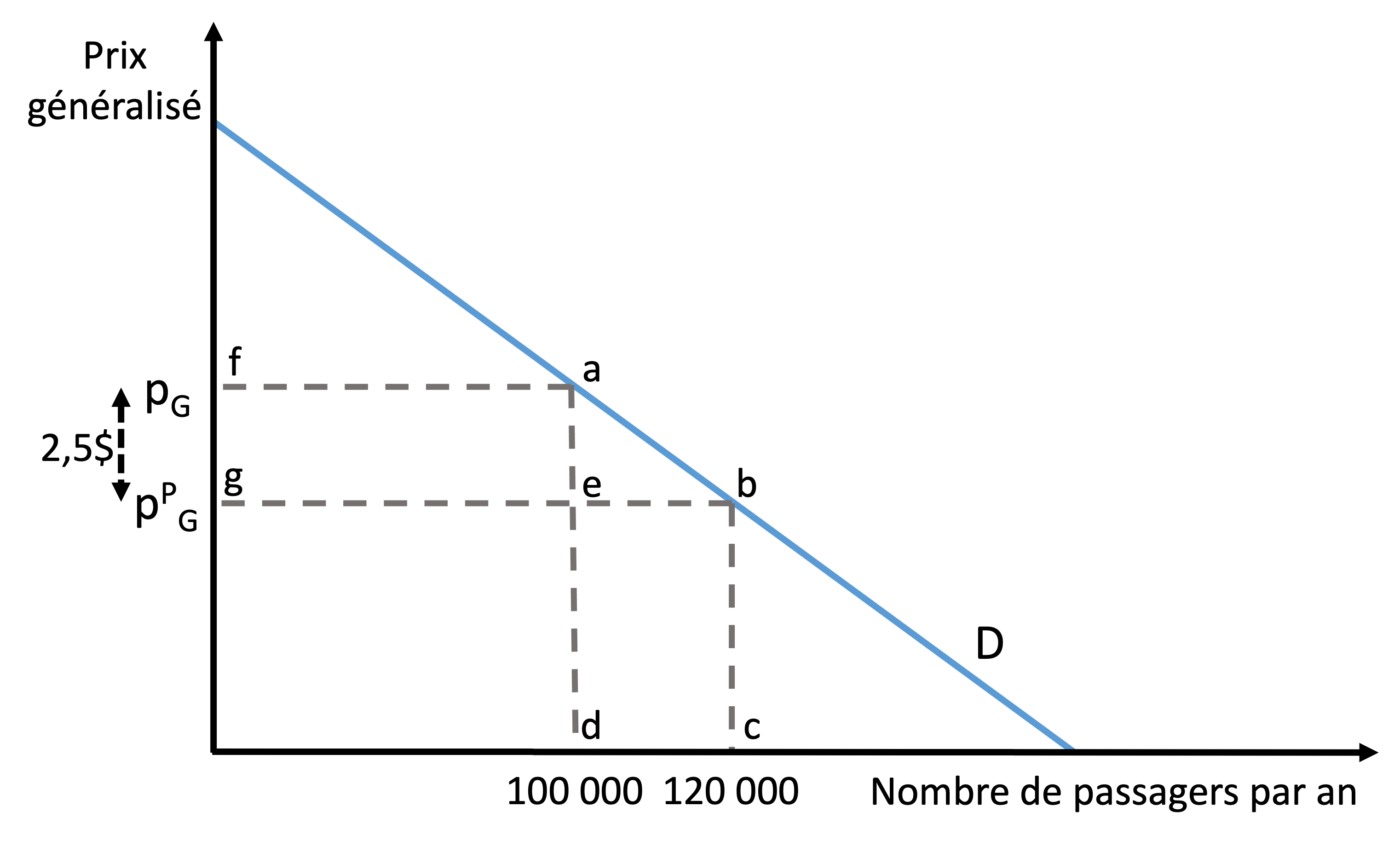
La courbe de la demande peut être représentée dans l’axe quantité-prix généralisé, comme l’illustre la Figure 7.6. Cette courbe de la demande se distingue de celle représentée à la Figure 7.5, qui illustrait la relation entre le nombre de passages et le prix du billet. Sur la Figure 7.6, le projet réduit le prix généralisé de 2,5 $, ce qui augmente la quantité demandée de 100 000 à 120 000. On obtient donc, dans ce cas, un déplacement le long de la courbe de la demande, plutôt qu’un déplacement de la courbe de la demande.

L’impact du projet sur les usagers se mesure par l’accroissement du SC, qui correspond à la surface fabg. Cette surface se compose de la surface faeg, qui mesure le gain de surplus des usagers courants et la surface aeb, qui saisit le surplus des nouveaux usagers. Naturellement, ces impacts ont les mêmes valeurs que celles obtenues en utilisant les données de la Figure 7.5. Cette présentation alternative est couramment employée dans les projets visant à améliorer les temps de déplacement.

*Figure 7.6 Impact du projet de transport considérant la demande en fonction du prix généralisé*

Attention : erreur possible !

Les ACA qui n’utilisent pas de cadre d’analyse formel commettent parfois l’erreur d’accorder la même valeur aux gains de temps des usagers actuels et aux nouveaux usagers. Dans notre exemple, cela équivaudrait à évaluer le surplus engendré par l’ajout de 20 000 usagers supplémentaires à 2,5 $ au lieu de 1,25 $. Dans certaines circonstances, cette approximation pourrait être jugée acceptable, particulièrement si le trafic induit demeure faible par rapport au trafic existant. Cette « erreur » se manifeste dans l’étude du pont enjambant le Saguenay et entraîne une surévaluation des gains de temps de 10 %.

7.3 Le projet ajoute à l’offre dans un marché

Un projet peut directement contribuer à accroître l’offre d’un bien qui est déjà négocié dans un marché concurrentiel. Comme nous allons le démontrer, la VAN d’un tel projet peut se calculer de diverses manières. L’objectif demeure toujours d’opter pour la méthode appropriée en fonction des données disponibles. De plus, nous allons dériver une règle d’évaluation pratique, simple et nécessitant un minimum de données. Une fois de plus, nous recourons à un exemple fictif, mais réaliste, afin d’illustrer notre analyse.

7.3.1 Exemple – une nouvelle usine de ciment

Afin de stimuler le développement économique d’une région donnée, le gouvernement envisage de soutenir l’établissement d’une nouvelle cimenterie destinée à desservir le marché national. Dans cette démarche, on suppose que le degré de concurrence est suffisant pour prévenir l’exercice d’un pouvoir de marché. Par conséquent, l’analyste considère qu’il est judicieux d’adopter le cadre conceptuel de l’offre et de la demande en situation de concurrence parfaite pour évaluer les répercussions de ce projet sur le marché du ciment. Afin de simplifier la présentation, nous procéderons à l’analyse sur une seule année^[6].

Les coûts annualisés de construction et d’exploitation d’une nouvelle usine sont évalués à 400 millions de dollars. À ce stade, nous limitons notre analyse aux impacts du projet sur le marché du ciment.

D’emblée, nous pouvons anticiper des conséquences sur trois groupes d’acteurs :

Les acheteurs de ciment qui pourraient éventuellement profiter d’une offre accrue sur le marché ;
Les producteurs de ciment existants qui devront faire face aux conséquences de l’arrivée d’une nouvelle usine ;
La nouvelle usine elle-même, qui devrait logiquement générer un surplus.

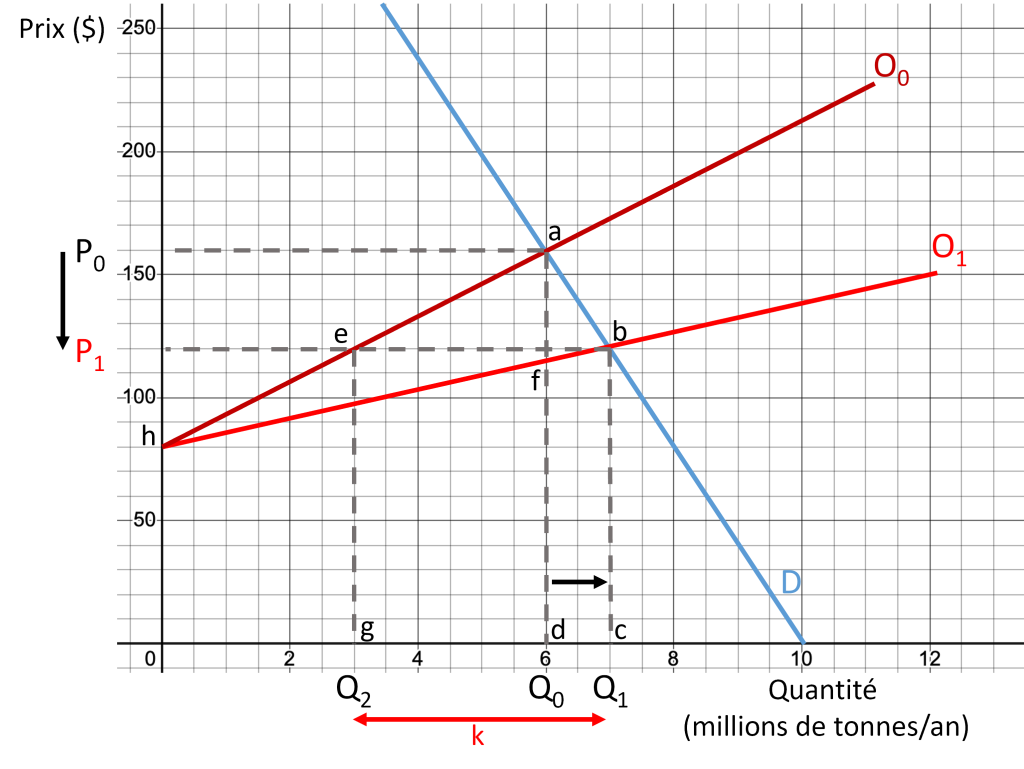
Examinons plus en détail ces impacts à partir du cadre conceptuel de l’offre et de la demande, en supposant que l’analyste connaît le positionnement des courbes. Ainsi, les courbes de demande (D) et d’offre initiale (O₀) sont représentées dans la Figure 7.7. Le projet implique l’ajout d’une nouvelle unité de production entraînant un déplacement de la courbe d’offre vers la droite (O₁)^[7].

De cette manière, nous observons que le projet engendre les conséquences suivantes :

Le prix du marché connaît une baisse, passant de P₀ = 160 $ à P₁ = 120 $ ;
La quantité totale échangée augmente, passant de Q₀ = 6 millions de tonnes à Q₁ = 7 millions de tonnes ;
Les producteurs existants réduisent leur production, passant de Q₀ = 6 millions de tonnes à Q₂ = 3 millions de tonnes, en réaction à la diminution du prix ;
La nouvelle usine comble la différence entre Q₂ et Q₁, soit 4 millions de tonnes de ciment.

*Figure 7.7 Impact du projet sur le marché du ciment*

Il est judicieux d’aborder cette problématique au moyen de l’approche sociale, car cela permettra de déduire une règle pratique simple. Avec cette approche, les trois éléments à évaluer sont les suivants :

La valeur sociale de la production additionnelle sur le marché se mesure sous la courbe de la demande entre Q₀ et Q₁, soit la surface abcd, qui équivaut à 140 millions de dollars ;
La valeur sociale des ressources épargnées par le projet est représentée par la surface eadg, évaluée à 420 millions de dollars. En effet, les producteurs déjà présents réduisent leur production de 6 millions à 3 millions de tonnes, ce qui libère des facteurs de production (travailleurs, énergie, capital), dont la valeur dans leur meilleure affectation alternative se mesure par la surface sous la courbe d’offre O₀ entre Q₀ et Q₂ ;
Le coût social du projet correspond aux coûts d’investissement et d’exploitation de la nouvelle usine, soit 400 millions de dollars annuellement^[8].

La valeur nette du projet dans le marché du ciment se chiffre ainsi à 160 millions $/an. À titre d’exercice, vous pouvez vérifier si l’approche par partie permet de trouver la même VAN (voir l’exercice 1).

7.3.2 Une règle de pratique

Une fois de plus, il est essentiel de rappeler que l’analyste ne dispose pas d’un graphique affichant les courbes d’offre et de demande parfaitement dessinées telles qu’elles sont représentées à la Figure 7.7. Cependant, il est possible d’appliquer une règle de pratique faisant usage d’éléments dont l’analyste devrait normalement disposer. Ces éléments sont répertoriés dans le Tableau 7.3.

**Tableau 7.3 Les données disponibles pour effectuer l’ACA**
Variable	Valeur
Prix courant du marché (observé)	160 $/tonne
Élasticité-prix de la demande (état des connaissances)	2/3
Élasticité-prix de l’offre (état des connaissances)	2
Quantité courante (observé)	6 millions de tonnes par an
Quantité mise en marché par le projet (estimé)	4 millions de tonnes par an
Coût total annuel de la production du projet (coûts d’opération + coût d’investissement annualisé) (estimé)	400 millions de dollars par an

À partir de ces données, nous pouvons prévoir en premier lieu l’évolution du prix dans le scénario avec le projet. Pour ce faire, il suffit d’appliquer les formules exposées dans le chapitre 4 à la section 4. À titre de rappel, la réduction du prix induite par le projet peut être calculée comme suit :

[latex]\Delta p\ \% = - \left( \frac{k}{Q_0} \right) \times \left( \frac{1}{\eta_D + \eta_O} \right)[/latex]

Dans notre exemple, cela signifie une diminution de 25 % du prix, ce qui équivaut à un prix de 120 $ dans le scénario avec le projet. Conséquemment, suite à cette baisse, la quantité échangée sur le marché devrait augmenter de 16,6 %, soit [latex]\eta_D[/latex] x 25%. De plus, nous pouvons également anticiper la réduction de la quantité offerte par les producteurs déjà établis. La baisse de 25 % du prix devrait entraîner une diminution de 50 % de leur production, soit [latex]\eta_O[/latex] x 25%. Ces valeurs concordent avec celles obtenues grâce à l’analyse graphique.

Par ailleurs, il est important de noter que la somme des deux avantages identifiés dans l’approche sociale, à savoir la valeur sociale de la production additionnelle et celle des ressources épargnées, correspond à la surface eabcg figurant dans la Figure 7.7. Cela conduit à la formulation de la règle de pratique suivante^[9] :

La valeur sociale de la production d’un projet mis en œuvre dans un marché concurrentiel s’évalue approximativement^[10] à partir de la formule suivante :

Prix de référence x Quantité mise en marché par la nouvelle usine

avec le prix de référence = ½ (Prix avant le projet + Prix après le projet).

En d’autres termes, les avantages sociaux engendrés par la production du projet dans le marché correspondent à la quantité ajoutée par le projet, valorisée à l’aide d’un prix de référence équivalant à la moyenne du prix avant et après la mise en œuvre du projet.

Dans le contexte de l’approche sociale, la valeur ainsi calculée comprend la valeur brute de la production additionnelle et la valeur des ressources économisées à cause de l’évincement des producteurs déjà établis par le projet. Dans l’approche par partie, l’effet mesuré correspond à l’impact sur les consommateurs, sur les producteurs déjà établis et sur les revenus du nouveau producteur.

Dans notre exemple, la quantité mise en marché dans le projet s’élève à 4 millions de tonnes par an. Cette quantité doit être valorisée au prix moyen de 140 $/tonne, soit ½ (160 $+120 $). La valeur sociale de la production mise en marché par le projet s’élève donc à 560 millions de dollars. Cette valeur tient compte de l’impact du projet sur les consommateurs (hausse du SC) et sur les producteurs déjà établis (baisse du SP), de même que de l’effet sur les revenus du nouveau producteur. Il reste donc encore à soustraire les coûts du projet pour obtenir la VAN de 160 millions de dollars.

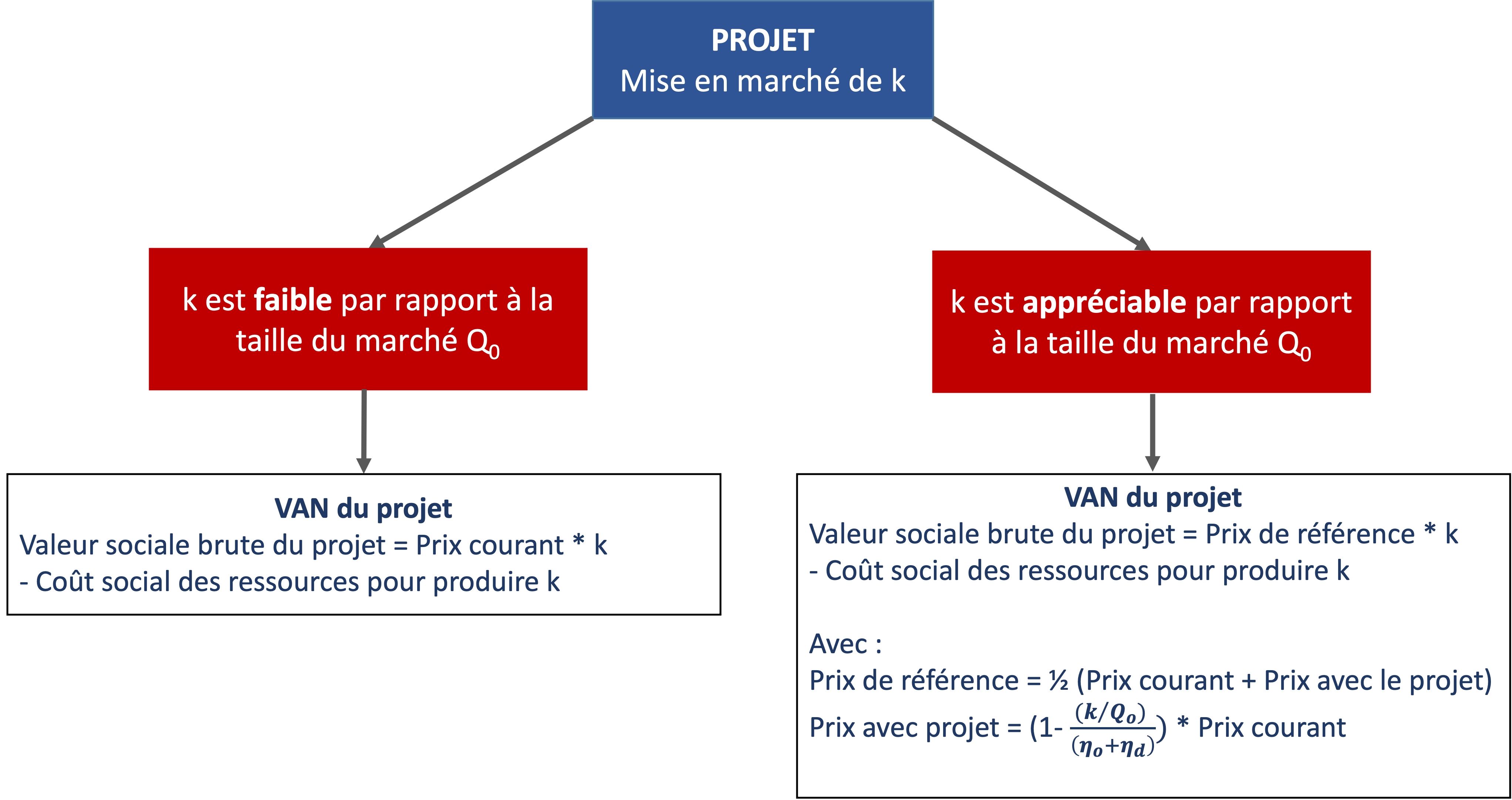
Enfin, il est important de noter qu’il peut arriver que le projet introduise sur le marché une quantité additionnelle relativement minime par rapport au volume total des échanges. Dans un tel cas, l’impact sur le prix d’équilibre (et par extension sur les consommateurs et les producteurs déjà établis) s’avère négligeable, simplifiant ainsi la valorisation, qui peut s’établir au prix courant sur le marché.

Si le projet met en marché une quantité k qui est petite relativement à la taille des échanges sur le marché (Q₀), la valorisation peut être déterminée approximativement en utilisant le prix d’équilibre initial sur le marché, soit P₀ * k.

La Figure 7.8 résume la règle de pratique pour valoriser les impacts d’un projet qui met en marché une quantité [latex]k[/latex] dans un marché concurrentiel.

*Figure 7.8 Règle de pratique pour la valorisation de mise en marché de k dans un marché sans distorsion*

7.4 Conclusions

Dans ce chapitre, nous nous sommes concentrés sur la valorisation des extrants d’un projet, en laissant de côté d’éventuelles distorsions. Dans les chapitres à venir, nous aborderons précisément la manière de les intégrer dans notre cadre d’analyse. À ce stade, les principaux éléments à retenir sont :

Éléments clés à retenir

Les avantages d’une nouvelle infrastructure s’évaluent sur la base du CAP des utilisateurs.
Le CAP correspond à l’aire située sous la courbe de la demande des usagers entre 0 et le niveau d’usage prévu.
L’estimation de la courbe de la demande d’une nouvelle infrastructure peut s’avérer difficile.
Comme le CAP se répartit entre différentes parties, il peut être possible d’évaluer une partie ou l’entièreté de ce montant en additionnant l’impact sur les différentes parties concernées (profit opérationnel, taxes récoltées par l’État, surplus du consommateur et coûts opérationnels).
Lorsqu’un projet altère la qualité d’un service, cela entraîne un déplacement de la courbe de la demande. La surface entre la courbe initiale et la nouvelle courbe quantifie l’impact sur les utilisateurs.
Dans le domaine des transports, les variations dans les temps des déplacements peuvent être considérées comme des fluctuations dans le prix généralisé, ce qui équivaut à des déplacements le long de la courbe de la demande, exprimée en fonction du prix généralisé.
Lorsque le projet contribue de manière significative à l’offre dans un marché concurrentiel, la valorisation sociale de la production mise en marché par le projet peut s’effectuer en utilisant un prix de référence correspondant au prix moyen sur le marché avant et après le projet. Cette valorisation permet de tenir compte de l’impact sur les consommateurs, sur les producteurs existants et sur le revenu du projet.
Si la quantité ajoutée par le projet est faible, la valorisation s’évalue approximativement en utilisant le prix du marché courant.

Retour sur la motivation

La ville d’Hamilton, Ontario, a décidé de remplacer sa ligne d’autobus express reliant l’Université McMaster à Eastgate Square par un système léger sur rail (SLR) plus moderne et efficace. Cette nouvelle ligne s’étendra sur une distance de 14 km et comportera 17 arrêts. Les principaux avantages du SLR sont :

Une vitesse de déplacement supérieure (34 km/h au lieu de 21 km/h) permettant des déplacements plus rapides ;
Une capacité accrue, afin de répondre à la forte croissance anticipée de la population ;
Un service plus confortable et ponctuel.

Quel cadre d’analyse utiliser pour valoriser ces extrants dans une ACA ?

Réponse

L’avantage principal de ce projet de transport réside dans les gains de temps qu’il procure aux utilisateurs. Le cadre élaboré dans la section 7.2.2 s’applique donc pour l’analyse de ce projet. L’analyste doit ainsi évaluer les économies de temps engendrées par le projet pour les utilisateurs actuels et mesurer l’impact du trafic induit. Par ailleurs, l’amélioration du confort peut être appréhendée à partir du cadre défini dans la section 7.2.1. Cela implique d’évaluer le consentement à payer des usagers pour un niveau de confort supérieur.

L’agence régionale de planification des transports pour la région du Grand Toronto, a publié une ACA de ce projet (Métrolinx, 2010). L’étude estime les gains de temps à environ 650 millions de dollars, ce qui représente 75% des bénéfices totaux du projet, évalués à 855 millions de dollars. Ces gains de temps ont été calculés grâce à un modèle de simulation mathématique des déplacements, prenant en compte non seulement les avantages pour les usagers des transports en commun mais également pour les automobilistes, grâce à la diminution de la congestion. Quant aux avantages liés au confort, ils ont fait l’objet d’une évaluation qualitative uniquement. Le coût total du projet est estimé à 784 millions de dollars.

Le chapitre 23 présente une étude de cas portant sur une réglementation entraînant une augmentation des coûts de production dans l’industrie du mazout et du diesel.

Le chapitre 24 présente une étude de cas détaillée sur l’ACA d’un projet combinant tramway et système d’autobus rapides pour la région de Québec.

Exercices

(*) Indique que la solution est disponible

(**) Indique que la solution est disponible en accès restreint

(*) Dans l’exemple de la nouvelle cimenterie, dans la section 7.3.1, vérifiez que l’approche par partie permet d’obtenir également une VAN = 160 millions de dollars. Distinguez les parties prenantes suivantes : les consommateurs, les producteurs déjà établis et la nouvelle usine.
(*) Une ligne de train de banlieue transporte en moyenne 75 000 usagers par année entre la banlieue et le centre-ville. Le prix de 15 $ par trajet couvre le coût moyen d’exploitation. Un projet vise à améliorer les voix, de sorte que la durée du trajet diminue de 45 minutes à 25 minutes. On estime que la valeur moyenne du temps des usagers du train est de 7 $/heure. De plus, on estime que l’élasticité de la demande par rapport au prix (ou au coût) généralisé est de 0,7. Le projet augmentera le coût moyen d’exploitation de 10 %, mais le prix du trajet ne sera pas modifié. En supposant une demande linéaire, déterminez la valeur de l’impact sur les usagers.
(**) Une municipalité de taille moyenne envisage de construire une usine de biométhanisation de ses déchets organiques. L’un des extrants du projet s’avère être du gaz naturel qui sera vendu sur le marché. À votre avis, à quel prix faut-il valoriser cet extrant ? Expliquez.
- Par ailleurs, le projet produira 400 tonnes d’engrais écologiques. Étant donné les coûts du transport, le marché des engrais écologiques est régional. Il est donc prévu que le projet double la production d’engrais écologique dans la région. On estime que la demande pour ces engrais a une élasticité-prix de 3, alors que l’élasticité de l’offre des engrais écologiques est de 0,1. Le prix actuel est de 250 $/tonne. Quelle est la valeur sociale que nous devons associer à la production d’engrais écologiques de la nouvelle usine ? Expliquez.
(*) Un musée des beaux-arts envisage d’accueillir une exposition de calibre international des œuvres d’Alberto Giacometti. L’exposition coûtera 1 million de dollars pour un événement de 4 mois. En considérant les résultats de cette exposition dans d’autres musées où elle a été présentée, on estime qu’elle devrait attirer 120 000 visiteurs de plus que le nombre de visiteurs anticipés s’il n’y avait que les expositions permanentes du musée. Les recettes additionnelles prévues (billetteries, stationnement et boutiques) sont évaluées à 1,2 million de dollars. Les coûts d’opération devraient cependant augmenter de 350 000 $. Quel devrait être le surplus d’un visiteur moyen pour que cette exposition se justifie par les bénéfices directs aux usagers ? Étant donné la courte durée de ce projet, il n’est pas utile d’actualiser.
(**) Un projet consiste à remplacer un système de traversiers entre deux rives par un pont. Le système de traversiers est opéré par la Société des traversiers. Le passage coûte 3 $. Le nombre de passages est de 100 000 par année. Les coûts d’opération du traversier sont évalués à 150 000 $ par année. Avec la construction du pont, le traversier pourra être revendu à un prix évalué à 25 millions de dollars. Le coût de construction du pont, évalué à t = 0, s’élèvera à 100 millions de dollars. Le passage sur le pont sera payant, à 5 $ le billet. On estime la valeur monétaire du temps sauvé grâce au pont à 12 $ en moyenne par passage. De plus, le nombre de passages devrait augmenter à 145 000 avec l’ouverture du pont et demeurer stable par la suite. Les coûts d’entretien et d’opération du pont sont évalués à 100 000 $/année. Le pont aurait une durée de vie de 75 ans. Le taux d’actualisation social serait de 5 %. Pour simplifier, on considère que le pont est construit à t = 0, et le traversier revendu à t = 0. On suppose aussi que les avantages et les coûts d’opération se réaliseront de manière continue chaque année, dès l’année 1. Effectuez une ACA de ce projet.

Bibliographie

Bourbonnais, R. et Usunier, L. (2017). Prévision des ventes (6e ed.). Economica.

Jenkins G.P., Kuo C. et Harberger, A.C. (2011). Cost-Benefit Analysis for Investment Decisions. https://agrilinks.org/sites/default/files/resource/files/cost-benefit_analysis_for_investment_decisions.pdf

Metrolinx (2010). Hamilton King-Main Benefit Case. https://www.raisethehammer.org/article/1016/hamilton_king-main_rapid_transit_benefits_case

Townley, P.G.C. (1998). Principles of Cost-Benefit Analysis in a Canadian Context. Prentice Hall Canada.

D’autres intervenants, comme l’État, peuvent aussi s’approprier une partie du CAP, par exemple, s’il y a une taxe sur le prix d’entrée. ↵
On pourrait aussi évoquer des arguments d’ordre positif pour expliquer l’intervention de la municipalité. Celle-ci peut vouloir attirer une nouvelle source de taxes foncières. Elle pourrait aussi y voir l’occasion d’augmenter son attrait auprès de nouveaux résidents, ce qui pourrait amplifier ses rentrées fiscales. ↵
Soulignons que la ligne ef dans la Figure 7.2 ne représente pas la courbe de coût variable moyen comme celles qu’on peut observer au chapitre 4. En effet, la Figure 7.2 ne fournit aucune information sur comment le coût moyen d’exploitation évolue en fonction du nombre d’entrées. Il serait erroné d’inférer (sans validation adéquate) que les coûts d’exploitation s’élèveraient à 50 000 $ lorsque le nombre d’entrées atteindrait 10 000. Comme indiqué précédemment, il est probable qu’une grande partie des coûts d’exploitation seraient quasi-fixes, de sorte que le coût moyen d’exploitation serait probablement plus élevé que 5 $. ↵
Il faudrait peut-être aussi tenir compte du coût marginal des fonds publics. En revanche, une part importante des revenus des municipalités provient des taxes foncières, qui créent relativement peu de distorsion. ↵
Notons qu’il n’est pas nécessaire de prendre en compte le changement des profits d’opération, puisque le prix du billet couvre le coût d’exploitation (avant et après le projet), de sorte que le profit est nul. ↵
Cela suppose que le marché demeure stable dans le temps, ce qui constitue évidemment une hypothèse restrictive. Dans la réalité, il faudrait prévoir l’évolution des prix pendant la durée de vie du projet, avec et sans le projet. ↵
Pour simplifier, nous supposons tous les coûts variables, de sorte que les courbes d’offre correspondent aux courbes du coût marginal à long terme. De cette manière, les surfaces sous les courbes d’offre mesurent le coût total. ↵
Il convient de noter que cette valeur n’est pas facile à visualiser dans la Figure. Elle peut être obtenue en calculant la différence entre le coût total avec le projet, la surface hbco sous la courbe O₁ entre 0 et Q₁, et le coût de production des producteurs déjà présents, la surface hego sous la courbe O₀ entre 0 et Q₂. ↵
Voir aussi Jenkins et al. (2011). ↵
La formule n’est exacte que si les courbes d’offre et de demande sont linéaires. ↵

Licence

Symbole de Licence Creative Commons Attribution 4.0 International