6 L’actualisation et les règles de décision
Motivation et objectifs d’apprentissage
Dans le cadre de vos fonctions, vous devez choisir entre deux projets qui s’excluent mutuellement. Le projet A procure un avantage annuel de 30 000 $ et entraîne un coût annuel de 12 000 $ pendant 5 ans. Le projet B occasionne un coût de 25 000 $ la première année, puis un coût annuel de 5000 $ de la deuxième année à l’année 10. Ce projet générera par ailleurs un avantage annuel de 30 000 $ pendant 10 ans. Quel projet sélectionneriez vous en supposant un taux d’actualisation de 5 % ?
Bien que ces deux projets procurent le même avantage annuel de 30 000 $, leur structure de coût est différente, avec le projet A qui coûte moins que le projet B la première année, mais qui devient plus onéreux par la suite. De plus, ces deux projets ont des durées de vie différentes : 5 ans pour le projet A et 10 ans pour le projet B. Enfin, il est également possible qu’aucun de ces deux projets ne soit rentable. Les techniques d’actualisation présentées dans ce chapitre vous permettront de résoudre ce choix.
À la fin de ce chapitre, vous serez capable de :
- Maîtriser le mécanisme et l’interprétation de l’actualisation ;
- Comparer des projets qui ont des horizons temporels différents ;
- Comprendre les défis relatifs à l’établissement de la valeur résiduelle d’un projet ;
- Neutraliser les effets de l’inflation ;
- Appliquer les bonnes règles de sélection des projets ;
- Éviter de comptabiliser plusieurs fois les coûts associés à un bien durable.
Dans ce chapitre, nous n’abordons pas la question du choix du taux d’actualisation social. Cet enjeu sera traité au chapitre 17.
6.1 Pourquoi faut-il actualiser ?
Pourquoi 1 000 $ aujourd’hui valent-ils plus que le même montant dans dix ans ? Deux raisons expliquent ce phénomène :
- L’inflation ;
- Le coût de renonciation des ressources investies.
L’inflation signifie une hausse générale des prix, de sorte que le pouvoir d’achat de 1 000 $ s’effrite avec le temps. L’actualisation permet de soustraire les effets de l’inflation. Toutefois, il est également possible de neutraliser cet effet en travaillant avec des séries de données qui sont exprimées en valeur réelle de l’année de référence (ou en valeur constante). L’inflation n’est donc pas la raison fondamentale qui justifie le recours aux techniques d’actualisation.
En fait, l’objectif principal de l’actualisation consiste à prendre en compte le coût de renonciation des ressources investies dans un projet. En effet, elles pourraient être :
- Investies dans un autre projet qui procurerait un certain taux de rendement ;
- Utilisées pour de la consommation courante apportant des avantages immédiats.
Ainsi pour qu’un projet soit considéré comme rentable, il faut qu’il produise un taux de rendement supérieur à ce qu’il serait possible d’obtenir dans son meilleur usage alternatif. Le taux d’actualisation est le paramètre qui capte ce coût de renonciation. Par ailleurs, dans la mesure où l’ACA adopte une perspective sociale, il faut utiliser un taux d’actualisation social.
Si le taux d’actualisation social est de 7 %, cela signifie qu’un projet aura une VAN positive uniquement si son taux de rendement interne est supérieur à 7 %, comme nous allons le montrer dans un exemple, dans la prochaine section.
6.2 Les formules d’actualisation
Nous commençons par le cas simple d’un projet qui s’étend pendant une période. Le plus souvent dans les ACA, une période correspond à une année. Imaginons donc un projet qui nécessite un investissement de 1 million de dollars aujourd’hui à t = 0, mais qui rapportera un avantage de 1,07 million de dollars dans un an, soit à t = 1. L’année de référence de l’ACA de ce projet est t = 0. La Figure 6.1 illustre le déroulement temporel du projet.

Comme nous l’avons expliqué au chapitre 1, ce projet doit être évalué par rapport à un scénario de référence. Il faut donc se questionner sur le meilleur usage alternatif du montant de 1 million de dollars du projet. Nous l’avons indiqué dans la section précédente, le montant pourrait être investi dans un autre projet ou servir à la consommation actuelle. Plutôt que d’essayer de déterminer précisément le meilleur usage alternatif de ce montant, il suffit d’établir le taux de rendement social espéré si les fonds étaient investis autrement. Ce taux correspond au taux d’actualisation social, représenté par la lettre s.
Dans notre exemple, supposons que s = 5 %, soit 0,05. Le scénario de référence suppose alors que le million de dollars rapportera un avantage de 1,05 million de dollars à t = 1, s’il est utilisé dans un autre projet. Il s’agit d’une application de la formule du calcul des intérêts :
V1 = V0 x (1 + s)
dans laquelle V1 représente la valeur future à t=1 et V0 la valeur actuelle ou valeur présente à t=0.
Le Tableau 6.1 illustre les coûts et les avantages du scénario de référence et du scénario avec projet. Nous utilisons ici le format de présentation dans lequel on compare côte à côte les deux options.
| Investir dans le projet | Investir dans sa meilleure alternative | ||
| Coût (t = 0) | 1 | Coût (t = 0) | 1 |
| Avantage (t = 1) | 1,07 | Avantage (t = 1) | 1,05 |
Le coût initial est identique dans les deux scénarios, cependant, le projet offre un avantage supplémentaire de 0,2 million de dollars à t=1. Le Tableau 2 présente les résultats différemment, afin de faire ressortir le coût de renonciation du projet, soit l’avantage de 1,05 million de dollars auquel on renonce et qui est déterminé par le taux d’actualisation social.
| ACA du projet | Valeur future (en millions de $) |
| Avantage du projet (t = 1) | 1,07 |
| Coût de renonciation (t = 1) | 1,05 |
| Valeur future nette (VFN) (t = 1) | 0,02 |
Notons que dans la Tableau 6.2, toutes les valeurs sont exprimées en valeur future, soit à t = 1. Dans l’ACA, les résultats sont exprimés en valeur actuelle, soit à t = 0. Pour y parvenir, il suffit d’inverser la formule précédente :
[latex]V_0 = \frac{V_1}{1+s}[/latex]
Le Tableau 6.3 applique cette formule aux valeurs contenues dans le Tableau 6.2. Évidemment, le coût de renonciation exprimé à t = 0 n’est rien d’autre que le coût initial du projet. Les avantages actualisés sont de 1,019 million de dollars, de sorte que la VAN est égale à 0,019 million de dollars, ce qui correspond à la valeur actualisée de la valeur futur nette, soit 0,02/(1 + 0,05) = 0,019 million de dollars.
| ACA du projet | Valeur actualisée (en millions de $) |
| Avantage du projet en valeur actuelle (t = 1) | 1,019 |
| Coût de renonciation en valeur actuelle (t = 1) | 1 |
| Valeur actualisée nette (VAN) (t = 1) | 0,019 |
En résumé :
Les formules peuvent se généraliser à plusieurs périodes. Il faut ici tenir compte du fait que les intérêts sont composés : les intérêts accumulés génèrent à leur tour des intérêts. Ainsi une somme V0 placée pendant N années à un taux de s %, vaudra à t = N :
[latex]V_N = V_0 \times \left(1+s\right)^N[/latex]
En inversant cette formule, nous obtenons la valeur actuelle (V0) d’un montant perçu dans N période (VN) en supposant un taux d’actualisation s.
[latex]V_0 = \frac{V_N}{\left(1+s\right)^N}[/latex]
Cette formule peut s’appliquer à un avantage ou à un coût futur. Ainsi, la VAN d’un projet ayant un horizon temporel de N périodes se détermine par la formule suivante :
[latex]VAN = \frac{A_0}{\left(1+s\right)^0} + \frac{A_1}{\left(1+s\right)^1} + \dots + \frac{A_N}{\left(1+s\right)^N} - \left( \frac{C_0}{\left(1+s\right)^0} + \frac{C_1}{\left(1+s\right)^1} + \dots + \frac{C_N}{\left(1+s\right)^N}\right)[/latex]
ou sous une forme plus compacte :
[latex]VAN = \sum_{t=0}^N \frac{A_t}{\left(1+s\right)^t} - \sum_{t=0}^N \frac{C_t}{\left(1+s\right)^t} = \sum_{t=0}^N \frac{A_t - C_t}{\left(1+s\right)^t} \quad (6.1)[/latex]
avec [latex]A_t[/latex], l’avantage du projet perçu à la fin de la période t, et [latex]C_t[/latex] le coût du projet payé à la fin de la période t.
La VAN peut se calculer en actualisant séparément les avantages et les coûts ou en calculant pour chaque période l’avantage net, qui est ensuite actualisé. Notons que l’actualisation se fait généralement sur une base annuelle[2].
Il est important de décrire précisément le déroulement temporel des coûts et des avantages. La formule (6.1) suppose que le projet génère des coûts et des avantages dès le début du projet, soit à t = 0. Le plus souvent cependant, un projet comporte des coûts importants au début, puis des coûts d’exploitation par la suite, alors que les avantages n’apparaissent qu’après un certain nombre de périodes.
Outre le déploiement des avantages et des coûts au cours des années, il faut préciser le moment où les avantages et les coûts se présentent dans une année. Trois situations sont possibles (voir aussi la Figure 6.2) :
- L’impact (coûts ou avantages) se manifeste à la fin de chaque année. Dans ce cas, [latex]A_{10}[/latex], par exemple, est perçu à la fin de l’année 10, de sorte qu’il doit être actualisé sur 10 années, soit [latex]A_{10}/\left(1+s\right)^{10}[/latex] . C’est l’hypothèse utilisée par la formule (6.1) ;
- L’impact peut également se produire en début de chaque année. Ainsi, [latex]A_{10}[/latex] est censé être perçu au début de la dixième année, soit après 9 années, ce qui signifie que sa valeur actualisée est [latex]A_{10}/\left(1+s\right)^9[/latex] ;
- L’impact peut également se produire tout au long d’une année. Si [latex]A_{10}[/latex] est perçu graduellement tout au long de l’année, cela revient à supposer que [latex]A_{10}[/latex] arrive à t = 9,5, c’est-à-dire au milieu de l’année 10. Dans ce cas, sa valeur actualisée serait de [latex]A_{10}/\left(1+s\right)^{9,5}[/latex].
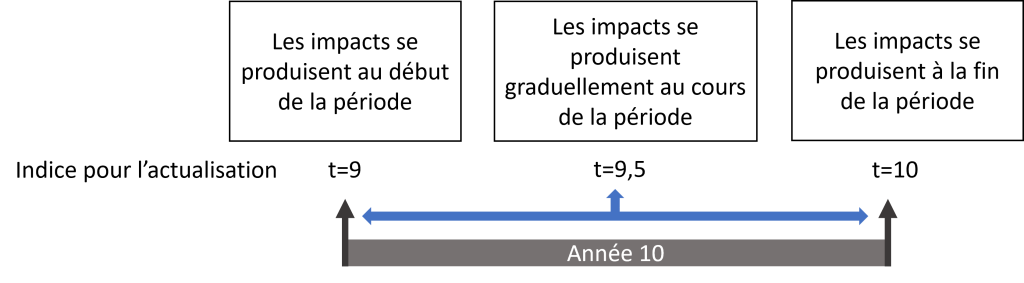
Figure 6.2 Différentes hypothèses concernant le déroulement des impacts au cours d’une période
6.3 Annuité, perpétuité et annualisation
6.3.1 L’annuité
Il est possible que les avantages ou les coûts soient des montants annuels qui ne varient pas avec le temps, de sorte que [latex]A_t = A[/latex] ou [latex]C_t = C[/latex], soit des annuités. La formule (6.1) peut bien entendu être utilisée, mais il existe une formule plus directe. La valeur actualisée d’une annuité A qui se réalise à la fin de chaque période pendant N périodes en utilisant le taux d’actualisation s est donnée par :
[latex]VA \left( A \right) = A \times a_s^N \quad (6.2)[/latex]
avec [latex]a_s^N = \frac{1 - \left(1+s\right)^{-N}}{s}[/latex] le facteur d’annuité.
Si l’annuité est reçue au début de chaque période plutôt qu’à la fin, le facteur d’annuité devient : la valeur actualisée peut être calculée comme suit :
[latex]a_s^N = \frac{1 - \left(1+s\right)^{-N}}{s} \times (1 + i)\quad (6.3)[/latex]
Dans le cas où l’annuité est perçue de façon continue tout au long de chaque période, le facteur d’annuité devient :
[latex]a_s^N = \frac{1 - \left(1+s\right)^{-N}}{s} \times (1 + i)^{0.5}\quad (6.4)[/latex]
Exemple : la valeur actualisée des coûts d’exploitation
Les coûts d’exploitation annuels d’un projet sont évalués à 100 000 $ pendant 5 ans. Ils doivent être supportés à la fin de chaque période. Calculez la valeur actualisée à un taux d’actualisation de 7 %.
Réponse
Le facteur d’annuité a la valeur [latex]a_{7\%}^5 = 4,1[/latex], de sorte que la valeur actualisée des coûts d’exploitation est de 410 000 $.
Dans certaines circonstances, le montant annuel de l’annuité n’est pas constant, mais il croît (ou décroît) à un taux constant de g %. Par exemple, l’avantage est reçu à la fin de la première période, mais il augmente annuellement de g %, de sorte que le montant reçu à la fin de l’année t est :
[latex]A_t = A_{t-1} \left(1+g\right) = A_{t-2} \left(1+g\right)^2 = \dots = A_1 \left(1+g\right)^{t-1}[/latex]
Dans ce cas, la valeur actualisée peut s’évaluer en utilisant la formule de l’annuité constante, soit (6.2), mais en l’appliquant sur le montant annuel suivant :
[latex]A = \frac{A_1}{1+g}[/latex]
et en utilisant le taux d’intérêt qui suit :
[latex]i = \frac{s-g}{1+g}[/latex]
Précisons qu’il faut que [latex]s>g[/latex] pour que cette procédure soit valide.
Par ailleurs, si g est relativement faible, on peut approximer la valeur actualisée en utilisant la formule (6.2), avec l’annuité et le taux d’intérêt suivants :
[latex]A = A_1[/latex] et [latex]i = s-g[/latex].
Exemple : Des avantages qui augmentent avec la population
Les avantages d’un projet sont évalués à 200 000 $ à la fin de la première année. On estime qu’ils vont ensuite croître au même rythme que la population, soit de 1 % par année. Le projet dure pendant 10 ans, et le taux d’actualisation social est de 5 %. Calculez la valeur actualisée de ces avantages.
Réponse :
La valeur actualisée de cette annuité croissante peut s’évaluer en utilisant la formule (6.2) sur une annuité équivalente à A = 200 000/(1 + 0,01) = 198 020 $ et en utilisant un taux d’actualisation i = 0,04/1,01 = 3,96 %. Avec ces paramètres, le facteur d’annuité est de 8,13, de sorte que la VA = 1 609 903 $.
En appliquant l’approximation, A = 200 000 et i = 4 %, de sorte que le facteur d’annuité est de 8,11 et la VA = 1 622 000 $.
6.3.2 La perpétuité
La valeur actualisée d’un montant de 1 000 $ reçu à la fin de chaque année pour toujours à un taux d’actualisation de 5 % est :
[latex]VA = 1000\$ \times a_{5\%}^{\infty} = \frac{1000\$}{0,05} = 20 \ 000\$[/latex]
En effet, le facteur d’actualisation s’étendant sur un horizon infini a une valeur égale à [latex]1/s[/latex]. Cette formule peut être utile pour effectuer une approximation dans des situations pour lesquelles l’horizon temporel est long.
6.3.3 L’annualisation
Dans certaines applications, il peut être nécessaire d’annualiser un coût ou un avantage, c’est-à-dire de le répartir sur une base annuelle pour la durée du projet. Cela peut se faire simplement en inversant la formule (6.2) ; par exemple, un projet exige un investissement initial à t = 0 de 20 000 $ et sa durée de vie est de cinq ans. L’annualisation de ce coût à un taux d’actualisation de 6 % se calcule de la manière suivante :
[latex]A = \frac{20 \ 000\$}{a_{6\%}^5} = 4 \ 747,9\$[/latex]
En d’autres termes, la valeur actualisée de l’annuité de 4 747,9 $ à 6 % est égale à 20 000 $.
6.4 Comparer des projets avec des horizons temporels différents
Il est parfois nécessaire de comparer des projets qui ont des durées différentes. Prenons l’exemple de la lutte contre la propagation d’une maladie contagieuse pour laquelle deux vaccins sont disponibles. Le vaccin 1 coûte 15 $ la dose et procure de l’immunité pendant un an, alors que le vaccin 2 coûte 70 $, mais offre une immunité équivalente pendant 5 ans. Pour simplifier, nous supposons que le coût par dose comprend à la fois le vaccin et son administration. Le choix entre ces deux options peut s’appuyer uniquement sur le coût, puisque l’efficacité des vaccins est la même. En revanche, les horizons temporels diffèrent : le vaccin 1 protège pendant un an, tandis que le vaccin 2 protège pendant 5 ans. Il existe trois méthodes pour comparer des projets ayant des horizons différents.
6.4.1 La méthode de réplication (roll over)
Pour comparer le coût du vaccin 1 pendant la même durée que le vaccin 2, il suffit d’administrer le vaccin 1 chaque année pendant cinq ans, c’est-à-dire de répliquer ce projet à 5 reprises. Cependant, il est important de noter qu’il ne s’agit pas simplement de multiplier par cinq le coût du vaccin 1, car il faut prendre en compte l’actualisation. Par exemple, avec un taux d’actualisation de 5 %, le coût total du vaccin 1 administré à cinq reprises équivaut à :
VA (vaccin 1 administré annuellement pendant 5 ans) = [latex]15\$ \times a_{5\%}^5 = 64,95\$[/latex]
Le vaccin 1 se révèle donc l’option la moins coûteuse.
6.4.2 La méthode par équivalent annuel moyen
Il s’agit de calculer, pour chaque option, l’Équivalent Annuel Moyen (ÉAM), c’est-à-dire d’annualiser la valeur actualisée nette. Dans notre exemple, le coût annuel moyen du vaccin 1 est par définition de 15 $. Pour calculer le coût annuel moyen du vaccin 2, il suffit d’appliquer la formule d’annualisation présentée à la section 6.3.3.
Coût annuel moyen du vaccin 2 = [latex]\frac{70\$}{a_{5\%}5} = 16,16\$[/latex]
Les deux méthodes, bien entendu, aboutissent à la même recommandation.
6.4.3 Inclusion d’une valeur résiduelle dans le projet le plus long
Il est parfois nécessaire de comparer des options pour lesquelles la réplication est peu réaliste. Dans ce cas, on peut calculer la VAN de l’option la plus longue, mais en utilisant l’horizon temporel de l’option la plus courte. C’est donc comme si l’on considérait que l’option la plus longue se termine de manière prématurée. Il faut alors inscrire la valeur résiduelle de ce projet dans les avantages (voir section 5.7 pour plus de détails).
6.5 La prise en compte de l’inflation
L’inflation désigne la hausse générale des prix au fil du temps et la déflation le phénomène inverse. Dans l’analyse coûts‑avantages (ACA), l’objectif consiste à neutraliser l’inflation (ou la déflation). La méthode classique pour éliminer les effets de l’inflation est de travailler avec des séries exprimées en dollars constants ou réels, plutôt qu’en dollars courants ou nominaux. Pour convertir une série nominale en valeur réelle, il est nécessaire de corriger l’effet de l’inflation à l’aide d’un indice des prix. Plusieurs indices de prix existent, mais voici les deux principaux :
- L’indice des prix à la consommation (IPC) mesure l’évolution des prix d’un panier type de biens et services consommés par les ménages. Pour l’année de base ou de référence, cet indice a une valeur de 100. L’évolution des prix est ainsi exprimée relativement à l’année de base. Par exemple, en 2009, l’IPC (2002 = 100) était de 119,1, ce qui signifie que les prix ont augmenté de 19,1 % entre 2002 et 2009;
- L’indice des prix du produit intérieur brut (PIB) est plus global que l’IPC, car il reflète l’évolution des prix dans l’ensemble de l’économie, englobant ainsi non seulement les biens et services de consommation, mais également d’autres secteurs.
Le choix de l’indice dépend de la série qu’on souhaite transformer. Pour une série de prix d’un bien de consommation (par exemple, le prix des téléphones cellulaires), il est préférable d’utiliser l’IPC. En revanche, si la série concerne le prix d’un intrant (par exemple, le bois d’œuvre), l’indice des prix du PIB est plus approprié.
La transformation d’une série nominale en série réelle s’effectue assez simplement, comme l’illustre le Tableau 6.4. La ligne (1) représente l’évaluation du prix courant de l’essence dans la Capitale-Nationale. La ligne (2) indique l’évolution de l’IPC à Québec en prenant l’année 2002 comme référence. À partir de ces deux lignes, on peut calculer la ligne (3), qui représente l’évolution des prix réels en dollars de 2002. Pour cela, il suffit de diviser la ligne (1) par la ligne (2) et de multiplier par 100.
Il est possible que l’année de base de l’IPC fournie par les organismes de statistiques officielles ne corresponde pas à l’année de référence souhaitée pour exprimer les valeurs. Cependant, il est facile de changer l’année de base de l’IPC, comme le montre la ligne (4), en appliquant une règle de trois. Cette ligne est obtenue en divisant les valeurs de l’IPC de la ligne (1) par la valeur de l’IPC de la nouvelle année de référence, puis en multipliant par 100. Dans notre exemple, pour exprimer l’IPC en dollars de 2023, on divise donc la ligne (1) par 171,6. À partir de cet indice en dollars de 2023, il est possible de calculer la ligne (5), qui représente le prix réel de l’essence en dollars de 2023.
| 2000 | 2010 | 2020 | 2023 | |
| (1) Prix courant | 73,2 | 106,3 | 103,7 | 171,6 |
| (2) IPC ( 2002 = 100) | 95,8 | 114,8 | 131,6 | 151,7 |
| (3) Prix réels en $ de 2002 | 76,4 | 92,6 | 78,8 | 113,1 |
| (4) IPC (2023 = 100) | 63,2 | 75,7 | 86,8 | 100 |
| (5) Prix réels en $ de 2023 | 115,8 | 140,4 | 119,5 | 171,6 |
| Sources : Statistique Canada (2024) et Régie de l’énergie (2024) | ||||
Ainsi, toutes les séries des valeurs qui sont utilisées dans une ACA (y compris les projections et les prévisions) devraient être exprimées en dollars constants de l’année de référence. Si c’est le cas, l’actualisation s’effectue en utilisant un taux d’actualisation social réel, soit un taux qui exclut l’inflation.
Cependant, il est aussi possible de travailler avec des séries de prévisions exprimées en dollars courants. Dans ce cas, l’actualisation s’effectue avec un taux d’actualisation social nominal qui permet de neutraliser l’inflation.
La différence entre un taux réel et un taux nominal représente l’inflation anticipée sur l’horizon d’analyse. La relation exacte entre ces deux taux est la suivante :
[latex]s^r = \frac{s^n - m}{1+m}[/latex]
avec [latex]s^r[/latex] le taux d’actualisation social réel, [latex]s^n[/latex] le taux d’actualisation social nominal et [latex]m[/latex] le taux anticipé moyen d’inflation au cours de la période d’analyse.
Si [latex]m[/latex] est faible, la relation entre les deux taux peut s’approximer comme suit :
[latex]s^r = s^n - m[/latex]
6.6 La valeur résiduelle
Idéalement, l’horizon d’analyse doit correspondre à la durée de vie du projet. Cependant, pour des infrastructures à longue durée de vie, il peut être difficile d’effectuer des prévisions réalistes à long terme. Par ailleurs, certains projets comprennent plusieurs infrastructures ayant des durées de vie différentes. Ainsi, il arrive que la durée de l’analyse (représentée par T) soit plus courte que la durée de vie du projet (représentée par F). Par exemple, dans l’étude du cas du pont du Saguenay, l’horizon d’analyse est de 40 ans (T = 40), alors que la durée de vie du pont est de 100 ans (F = 100). La Figure 6.3 montre un autre exemple où la durée de vie du projet est de 10 ans et l’horizon d’analyse de 6 ans. L’ACA doit donc inclure la valeur résiduelle du projet pour les 4 années qui ne sont pas explicitement prises en compte dans l’analyse.
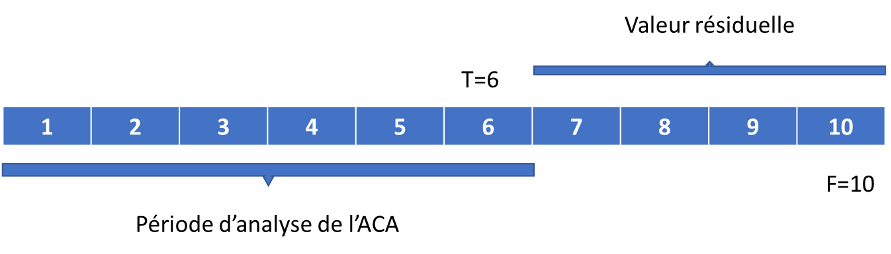
La valeur résiduelle constitue souvent un avantage (VR > 0) du projet, puisqu’elle correspond en quelque sorte à sa valeur de revente. Cependant, dans certains cas, la valeur résiduelle peut s’avérer négative (VR < 0) lorsque les coûts en fin de vie excèdent les avantages, comme cela peut être le cas d’une mine dont la qualité des dépôts diminuent avec le temps et qui exige des travaux de décontamination et de restauration des lieux.
La détermination de la valeur résiduelle d’un projet est une tâche délicate, d’autant plus qu’elle peut avoir un impact déterminant sur la VAN d’un projet. Plusieurs techniques d’évaluation sont possibles (voir Boardman et al., 2018).
6.6.1 L’évaluation par extrapolation
Conceptuellement, la VR d’un projet n’est rien d’autre que la valeur actualisée des avantages nets des coûts du projet entre la fin de la période d’analyse (T) et la fin de la durée de vie du projet (F), soit :
[latex]VR_T = \frac{B_{T+1} - C_{T+1}}{\left(1+i\right)^{T+1}} + \frac{B_{T+2} - C_{T+2}}{\left(1+i\right)^{T+2}} + \dots + \frac{B_{T+F} - C_{T+F}}{\left(1+i\right)^{T+F}}[/latex]
Notons que [latex]VR_T[/latex] mesure la valeur résiduelle du projet évaluée à T, de sorte qu’il faut encore l’actualiser pour la ramener en valeur de l’année de référence (voir la Figure 6.4). La valeur résiduelle qui doit être comprise dans l’ACA est donc :
[latex]VR_0 = \frac{VR_T}{\left(1+i\right)^T}[/latex]
Évidemment, si [latex]A_t[/latex] et [latex]C_t[/latex] entre T+1 et F sont connus, le projet peut simplement s’analyser sur la durée de vie du projet. La difficulté provient justement de la complexité d’estimer [latex]A_t[/latex] et [latex]C_t[/latex] entre T+1 et F.
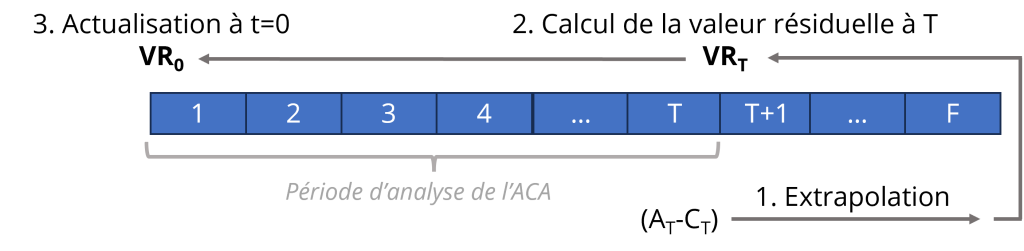
L’extrapolation la plus simple suppose que les avantages et les coûts mesurés à la fin de la période d’analyse resteront constants jusqu’à la fin du projet. Autrement dit, [latex]A_t = A_T[/latex] et [latex]C_t = C_T[/latex] pour tout t entre T+1 et F. Une autre option consisterait à considérer [latex]A_T[/latex] et [latex]C_T[/latex] comme des annuités qui augmenteront ou diminueront à un taux constant entre T+1 et F. La valeur résiduelle à T se calculerait alors en utilisant les formules présentées à la section 6.3.1. Cette valeur devrait ensuite être actualisée pour être exprimée en valeur de l’année de référence. Bien entendu, l’analyste devra justifier le réalisme et les implications de la technique d’extrapolation choisie.
6.6.2 L’évaluation fondée sur la valeur de revente
En effet, la valeur sur un marché secondaire reflète les avantages nets espérés sur le reste de la vie utile du bien durable. La valeur résiduelle d’un camion, par exemple, peut être estimée par sa valeur de revente à la fin de l’horizon d’analyse T. Cependant, il est essentiel de ne pas oublier d’actualiser cette valeur de revente à T, afin de l’exprimer en dollars de l’année de référence.
6.6.3 L’évaluation fondée sur la dépréciation économique
La dépréciation linéaire est la plus simple et la plus souvent utilisée dans un contexte fiscal. Le taux de dépréciation correspond simplement à l’inverse de la durée de vie de l’actif (1/F). Un ordinateur de 4 000 $ dont la durée de vie utile est de quatre ans aura un taux de dépréciation linéaire de 25 %, de sorte que sa valeur après trois ans sera de (1-3 x 0,25) x 4 000 $ = 1 000 $.
Une autre forme courante est celle de la dépréciation géométrique, dans laquelle l’actif se déprécie à un taux constant[4]. L’exercice ci-dessous illustre la formule de dépréciation géométrique. D’autres profils de dépréciation sont possibles, comme la dépréciation progressive, qui implique une accélération de la perte de valeur de l’actif avec le temps (par exemple, la dépréciation hyperbolique).
Exemple : La valeur résiduelle d’un camion

Un camion est acheté au coût de 1 million de dollars au début d’un projet. Selon Patry (2007), le taux de dépréciation géométrique de cette catégorie d’actif est de 21,2 % par année. Déterminez la valeur résiduelle du camion à inclure dans l’ACA du projet, si l’horizon d’analyse est de cinq ans et le taux d’actualisation est de 7 %.
Réponse
Comme la dépréciation est géométrique, la valeur résiduelle du camion à T = 5 se calcule comme suit :
[latex]VR \left( t = T \right) = 1 \text{million} \times \left(1 - 0,212\right)^5 = 303 \ 830\$[/latex]
En d’autres termes, le camion perd chaque année 21,2 % de sa valeur en début d’année.
La valeur résiduelle à inclure dans l’ACA doit être calculée à t = 0 :
[latex]VR \left( t = 0 \right) = \frac{303 \ 830\$}{\left(1 + 0,07\right)^5} = 216 \ 627\$[/latex]
6.6.4 La valeur résiduelle nulle
Si la période d’analyse est longue par rapport à la durée de vie du projet, il peut être justifié d’utiliser une VR nulle. En effet, la VR à la fin de la période d’analyse risque d’être faible, surtout lorsqu’elle est exprimée en dollars de l’année de référence. De plus, cette hypothèse est conservatrice, c’est-à-dire qu’elle penche du côté de la prudence.
Pour terminer, soulignons deux aspects importants :
-
L’analyste doit autant que possible justifier le choix du profil de dépréciation utilisé ;
-
Quelle que soit la méthode retenue pour établir la VR, il est important d’effectuer une analyse de sensibilité de la VAN par rapport à cette valeur. Si la rentabilité du projet dépend directement de sa valeur résiduelle, l’analyste doit le souligner et appeler les décideurs à la prudence.
Ce dernier point est parfaitement illustré par l’encadré ci-dessous concernant le projet de pont du Saguenay.
Étude de cas : La valeur résiduelle du pont du Saguenay
Lorsqu’ils ont évalué le projet de construction du pont sur le Saguenay, les experts ont regardé comment les choses se passeraient sur 31 ans, même si le pont est censé durer 100 ans. Pour prendre en compte la valeur du pont après ces 31 ans, ils ont utilisé un calcul simple : chaque année, le pont perd 1% de sa valeur initiale (dépréciation linéaire). Donc, à la fin des 31 ans, le pont vaut encore 69% de son coût de construction initial, qui était de 771 millions de dollars. Cela donne une valeur restante de 532 millions de dollars. Ils ont ensuite ajusté ce montant pour le ramener à ce qu’il vaudrait aujourd’hui, ce qui leur a permis de dire que le projet apporterait un avantage de 76 millions de dollars, soit 12% de l’avantage total du projet.
Cependant, cette méthode pose un problème : en calculant les choses de cette façon, on part du principe que les avantages du pont continueront de couvrir les coûts pendant toute la durée restante après les 31 ans, simplement parce que cette « valeur restante » est établie à partir du coût initial de construction. Si on poussait cette logique à l’extrême, en ne regardant pas du tout les avantages au fil du temps, mais seulement cette valeur restante, chaque projet semblerait ne pas perdre d’argent, ce qui n’est pas très logique.
Ce calcul favorise donc le projet. Les experts auraient dû proposer une analyse de sensibilité par rapport à la valeur résiduelle. Ils auraient pu notamment utiliser la méthode de détermination de la valeur par extrapolation, ce qui aurait rendu le projet encore moins rentable.
6.7 Critères et règles de décision
6.7.1 Des décisions basées sur la VAN
La décision de recommander ou non le projet doit se prendre sur base de la VAN. Trois types de décision peuvent appeler à des règles de décisions différentes :
Situation 1 : Réaliser ou non un projet
Situation 2 : Choisir entre des projets mutuellement exclusifs
Par exemple, pour connecter une ville, les autorités envisagent soit un système rapide d’autobus (SRB), un tramway ou un métro. Dans ce type de situation, la règle de décision est la suivante :
Dans notre exemple, si la VAN du SRB est évaluée à 120 millions, celle du tramway à 35 millions et celle du métro de -46 millions, il faut recommander le SRB. Précisons que la VAN de chaque option est toujours évaluée relativement au scénario de référence (p. ex. maintenir le système d’autobus actuel). Dans ce contexte cependant, le coût de renonciation du SRB est le meilleur projet alternatif auquel on renonce, soit le tramway. Ainsi, relativement au tramway, le SRB procure une VAN additionnelle de 85 millions.
Situation 3 : Choisir entre des projets avec une contrainte budgétaire
Dans cette situation, les projets ne sont pas mutuellement exclusifs, mais tous ne peuvent pas être réalisés en raison d’une contrainte budgétaire. Par exemple, le ministère des Transports dispose d’une enveloppe de 3 millions de dollars pour des projets d’amélioration de la sécurité routière. Le Tableau 6.5 montre la valeur actuelle des coûts et des avantages, ainsi que la VAN des quatre interventions. Par ailleurs, une cinquième option consiste à réaliser simultanément les interventions 3 et 4. Ces deux projets présentent des synergies positives de sorte que la somme des avantages de ces projets pris individuellement est inférieure à l’avantage si ces projets sont réalisés conjointement[5].
| Intervention | Valeur actualisée des avantages | Valeur actualisée des coûts | Valeur actualisée nette (VAN) |
| 1 | 1,9 | 0,7 | 1,2 |
| 2 | 2,7 | 2 | 0,7 |
| 3 | 2 | 1 | 1 |
| 4 | 1,5 | 1 | 0,5 |
| 3 et 4 | 4 | 2 | 2 |
Dans ce type de situation, la règle de décision est la suivante :
Pour des projets pour lesquels il existe une contrainte budgétaire, de sorte qu’ils ne peuvent pas tous être réalisés, il faut choisir la combinaison de projets pour laquelle la somme des VAN est la plus grande et dont la somme des coûts respecte la contrainte budgétaire.
Dans notre exemple, la combinaison des projets 1 et 3+4 conduit aux avantages nets les plus élevés, s’élevant à 3,2 millions de dollars tout en respectant la contrainte budgétaire. Le coût de ces deux projets est inférieur à 3 millions de dollars. En revanche, les deux autres combinaisons possibles (2+3 et 2+4) présentent des valeurs actuelles nettes moindres.
6.7.2 Le ratio avantage coût
Certaines études présentent les résultats sous forme du ratio avantage coût (A/C), qui est défini comme la valeur actualisée des avantages divisée par la valeur actualisée des coûts. Ce ratio est souvent significatif pour les autorités, par exemple, un ratio avantage coût de 3 permet aux autorités de soutenir que chaque dollar investi rapporte 3 dollars.
Ce ratio peut être utilisé pour déterminer si un projet doit être recommandé ou non. Un ratio supérieur à 1 signifie en effet que le projet génère une VAN positive. En revanche, lorsqu’il s’agit de choisir parmi une liste de projets mutuellement exclusifs ou s’il existe une contrainte budgétaire, l’utilisation du ratio A/C peut mener à des choix erronés.
Pour s’en convaincre, le Tableau 6.6 présente l’évaluation de trois projets mutuellement exclusifs. C’est le projet 1 qui doit être recommandé puisqu’il génère la VAN positive la plus élevée. Si le ratio A/C est utilisé, c’est le projet 3 qui serait malencontreusement choisi puisque son ratio est le plus élevé. En fait, le ratio A/C ne permet pas de comparer adéquatement des projets qui ont des envergures différentes.
| Projet | Valeur actualisée des avantages | Valeur actualisée des coûts | Valeur actualisée nette (VAN) | Ratio Avantage Coût (A/C) |
| 1 | 120 | 100 | 20 | 1,2 |
| 2 | 60 | 45 | 15 | 1,3 |
| 3 | 25 | 15 | 10 | 1,6 |
6.7.3 Le critère du taux de rendement interne
Le taux de rendement interne correspond au taux d’actualisation tel que la VAN calculée avec ce taux est nulle. Formellement, le taux de rendement interne [latex]\rho[/latex] s’obtient en résolvant l’équation suivante :
[latex]VAN = \sum_{t=0}^{n} \frac{A_t - C_t}{\left(1 + \rho \right)^t} = 0[/latex]
La règle de décision est alors de recommander le projet si le taux de rendement interne ([latex]\rho[/latex]) est supérieur au taux d’actualisation social (s). Par exemple, un projet coûte 100 millions à t=0 et rapporte à partir de t=1 une perpétuité de 15 millions par an. Le taux d’actualisation social est de 10%. Dans ce cas, [latex]\rho[/latex] s’obtient en résolvant l’équation suivante :
[latex]-100 + \frac{15}{\rho} = 0[/latex]
Le taux de rendement interne est donc de 15%, ce qui est supérieur au taux d’actualisation social de 10%; ce projet doit être recommandé. La VAN de ce projet s’élève à 50 millions.
Le taux de rendement interne est un indicateur qui est souvent utilisé dans l’évaluation de la rentabilité d’investissement privé. Il présente cependant plusieurs limites :
- Sauf cas particulier, la détermination de [latex]\rho[/latex] exige la résolution d’équations non-linéaires avec des solutions multiples, ce qui pose le défi de sélectionner le bon taux;
- Tout comme avec le critère du ratio A/C, choisir une option en se basant uniquement sur le taux de rendement interne le plus élevé ne permet pas de maximiser la VAN dans le cas de projets mutuellement exclusifs ou lorsqu’il y a une contrainte budgétaire (voir l’exercice 3 pour un exemple).
6.8 Le seuil de rentabilité ou le point mort
Il est souvent plus facile de recueillir des informations sur les coûts associés à un projet que sur ses avantages. Dans de tels cas, une méthode simple et efficace consiste à déterminer un seuil de rentabilité aussi nommé point mort. Ce seuil représente le niveau minimal que les avantages du projet doivent atteindre pour que la VAN soit nulle. Cette technique de détermination d’un seuil de rentabilité a déjà été mise en œuvre dans l’analyse coût-avantage de l’exposition temporaire présentée au chapitre 4.
Les formules d’actualisation exposées précédemment permettent de calculer ces bornes dans des situations plus complexes, comme l’illustre l’exercice ci-dessous.
Exercice : Le seuil de rentabilité d’un 3e lien
Afin de réduire la congestion, une ville considère la construction d’un troisième lien entre les deux rives du fleuve qui la traverse. Le projet est évalué à 4 milliards de dollars. L’horizon temporel est de 50 ans et le taux d’actualisation de 5 %.
- Déterminez l’avantage annuel moyen minimal pour que ce projet soit justifié.
- Sachant qu’il y a 152 000 passages par jour en moyenne entre les deux rives, et que ce nombre devrait augmenter d’environ 25 % avec la création du nouveau lien, quel devrait être l’avantage minimal moyen par passage pour justifier le nouveau pont.
- Sachant que les ventes totales d’essence se montent à 787 millions de litres par an dans la région et en supposant que le nouveau pont n’aura pas d’impact sur ce nombre de litres, calculez la taxe additionnelle par litre d’essence qu’il faudra imposer dans la région pour financer cette infrastructure.
Que pouvez-vous conclure sur la rentabilité sociale probable de ce projet ?
Réponse
- Il s’agit d’annualiser le coût de 4 milliards de dollars à un taux de 5 %, comme expliqué dans la section 6.3.3. En supposant que les avantages se produisent graduellement au cours de chaque année, le facteur d’annuité avec T = 50 et i = 5% s’évalue à 18,7. Par conséquent, l’avantage annuel minimal requis serait d’environ 214 millions de dollars par an (c’est-à-dire 4 milliards de dollars divisés par 18,7).
- Pour mettre ce montant en perspective, il est intéressant de le rapporter au nombre de passages annuels prévu si cette infrastructure est construite, soit 69 350 000 (152 000 x 1,25 x 365). Il faut donc qu’en moyenne le consentement maximal à payer par passage soit d’au moins 3 $.
- Si le financement se faisait en prélevant une surtaxe sur l’essence dans la région, celle-ci devrait s’élever à au moins 27 cents du litre.
6.9 La prise en compte du coût d’un bien durable
De nombreux projets ont recours à des intrants, qui sont des biens durables, c’est-à-dire des actifs qui peuvent être utilisés durant plusieurs années. Comment faut-il comptabiliser les coûts de ces biens durables dans une ACA ? Il existe plusieurs façons de prendre en compte le coût d’un bien durable, ce qui, par conséquent, engendre le risque d’enregistrer plusieurs fois le même coût. Pour illustrer ces approches et leur équivalence, prenons l’exemple du projet d’achat d’un nouvel appareil d’imagerie par résonance magnétique (IRM) par un hôpital.
Exemple : Un nouvel appareil d’IRM
6.9.1 Le coût d’usage annuel
Dans certains types d’analyses comme l’analyse financière ou fiscale, le coût de l’investissement est réparti sur sa durée de vie. Il s’agit alors d’évaluer le coût d’usage annuel de l’actif, soit en quelque sorte la consommation annuelle qui en est faite. Le coût d’usage annuel d’un actif comprend deux composantes :
-
L’amortissement ou la dépréciation économique, c’est-à-dire la perte de valeur de l’équipement au cours d’une année, à cause de l’usure et de l’obsolescence[6] ;
- Le coût de renonciation du capital, c’est-à-dire, comme nous l’avons déjà expliqué, le rendement auquel on renonce en maintenant cette immobilisation de capital pendant un an.
Dans notre exemple de l’IRM, supposons que la dépréciation économique se fasse vraiment de manière linéaire pendant 10 ans, avec une perte annuelle d’une valeur de 150 000 $. La valeur résiduelle de l’équipement, soit sa valeur de revente à la fin de chaque année, est calculée dans le Tableau 6.7. Il s’agit de la valeur résiduelle à la période précédente, moins l’amortissement. Avec un taux d’actualisation social de 5 %, le Tableau 6.7 présente le coût de renonciation annuel. Pour chaque année, il s’agit de la valeur résiduelle à la fin de la période précédente, multipliée par le taux de 5 %. Cela représente le rendement auquel on renonce en maintenant l’appareil en activité durant l’année plutôt que de le revendre. Par exemple, l’IRM pourrait être revendu 1,2 million de dollars à la fin de la deuxième année, et ce montant pourrait être réaffectées à un autre projet. Le coût de renonciation du maintient de l’IRM en service au cours de la troisième année est donc de 60 000 $. La somme de l’amortissement et du coût d’opportunité représente le coût d’usage annuel du bien durable.
Plus formellement, le coût d’usage d’un actif se mesure ainsi :
[latex]\text{Coût d'usage}_t = \left(\text{Valeur de l’actif}_{t-1} - \text{Valeur de l’actif}_t\right) + \text{i}\% \times \text{Valeur de l’actif}_t[/latex]
| Année | Valeur résiduelle | Amortissement économique | Coût de renonciation | Coût d’usage annuel |
| 0 | 1,5 | – | – | |
| 1 | 1,35 | 0,15 | 0,075 | 0,225 |
| 2 | 1,2 | 0,15 | 0,0675 | 0,2175 |
| 3 | 1,05 | 0,15 | 0,06 | 0,21 |
| 4 | 0,9 | 0,15 | 0,0525 | 0,2025 |
| 5 | 0,75 | 0,15 | 0,045 | 0,195 |
| 6 | 0,6 | 0,15 | 0,0375 | 0,1875 |
| 7 | 0,45 | 0,15 | 0,03 | 0,18 |
| 8 | 0,3 | 0,15 | 0,0225 | 0,1725 |
6.9.2 Le loyer implicite
Par ailleurs, l’hôpital pourrait louer l’IRM en payant un loyer annuel fixe ou encore en le finançant par un emprunt avec un remboursement constant. En utilisant le taux d’actualisation social, le loyer ou le remboursement annuel se détermine en annualisant le coût, soit :
[latex]\text{Loyer} = \text{Remboursement} = \text{A} = \frac{1,5m}{a_{5\%}^{10}} = 194 \ 256\$ \text{ par an}[/latex]
Il est donc possible de comptabiliser le coût de l’IRM sous la forme d’un montant annuel fixe correspondant à un loyer implicite.
6.9.3 La prise en compte de l’investissement lorsqu’il se réalise
Dans l’ACA, l’approche consiste généralement à comptabiliser le montant total de l’investissement lorsqu’il s’effectue. Dans notre exemple, il s’agit d’inclure le montant de 1,5 million de dollars à t = 0. Comme nous l’avons constaté précédemment, l’actualisation des avantages et autres impacts permettent de tenir compte du coût de renonciation.
Comme l’illustre le Tableau 6.8, ces trois approches sont équivalentes, dans la mesure où la VAN est identique. Le corollaire de ces équivalences est qu’il serait incorrect de comptabiliser à la fois l’investissement au moment où il se réaliser et d’y ajouter l’amortissement, le coût d’opportunité, les intérêts payés ou encore le loyer. Cela reviendrait à comptabiliser plusieurs fois le même coût.
| Année | Approche 1 | Approche 2 | Approche 3 |
| 0 | – | – | 1,5 |
| 1 | 0,225 | 0,1942 | |
| 2 | 0,2175 | 0,1942 | |
| 3 | 0,21 | 0,1942 | |
| 4 | 0,2025 | 0,1942 | |
| 5 | 0,195 | 0,1942 | |
| 6 | 0,1875 | 0,1942 | |
| 7 | 0,18 | 0,1942 | |
| 8 | 0,1725 | 0,1942 |
En résumé
Dans l’ACA, il faut généralement prendre en compte le montant investi dans un actif au moment où celui-ci se réalise. L’actualisation, l’horizon d’analyse et la valeur résiduelle permettent de prendre en compte l’amortissement et le coût de renonciation. Il ne faut donc pas comptabiliser en plus l’amortissement, les frais d’intérêts ou le paiement d’un loyer dans l’ACA.
Le Tableau 6.9 présente les résultats complets de l’ACA du projet d’IRM.
| Impact | Valeur annuelle | Valeur actualisée |
| Avantages | 3 000 000 $ | |
| Coût d’achat | 1 500 000 $ à t = 0 | 1 500 000 $ |
| Coûts d’exploitation | 150 000 $ de t = 1 à t = 10 | 1 158 300 $ |
| VAN = | 341 700 $ |
6.10 Conclusions
Éléments clés à retenir
- L’actualisation permet de ramener à un même référentiel de temps des impacts qui se produisent à différents moments.
- L’actualisation permet de prendre en compte le coût de renonciation des fonds investis dans un projet. La VAN d’un projet ne sera positive que si le projet démontre une rentabilité interne supérieure au taux d’actualisation social.
- Le taux d’actualisation social mesure le coût de renonciation des ressources investies dans un projet, soit ce qu’elles pourraient rapporter dans leur meilleur usage alternatif.
- Si l’horizon d’analyse est moins long que la durée de vie de certains actifs du projet, il faut inclure la valeur résiduelle de ces actifs dans l’ACA. Ces valeurs peuvent être établies sur la base d’une extrapolation des avantages et des coûts, et de leurs valeurs de revente, ou en utilisant une évaluation de leur taux de dépréciation économique.
- Pour comparer des projets qui ont des horizons temporels différents, on peut avoir recours à la méthode de la réplication, à l’équivalent annuel moyen ou analyser le projet le plus long sur l’horizon du plus court, avec l’ajout d’une valeur résiduelle.
- La règle de sélection d’un projet dépend du caractère mutuellement exclusif ou non des projets comparés et de l’existence d’une contrainte budgétaire.
- Le critère de décision doit s’appuyer sur la VAN, car le ratio avantage‑coût et le taux de rendement interne ne permettent pas toujours de sélectionner le bon projet.
- Dans les situations où l’on manque de données complètes pour calculer précisément la VAN ou lorsqu’une évaluation rapide d’un projet est nécessaire, il est recommandé de déterminer le seuil de rentabilité du projet. Ce seuil correspond à l’avantage annuel moyen minimum requis pour atteindre une VAN de zéro.
-
Dans l’ACA, le coût d’un bien durable est généralement pris en compte entièrement lorsque celui-ci est dû. L’amortissement, le coût d’opportunité du capital et le loyer implicite sont des méthodes alternatives de prise en compte du coût d’un bien durable. L’analyste doit être vigilant, afin d’éviter de comptabiliser plusieurs fois le coût d’un bien durable.
Retour sur la motivation
Dans le cadre de vos fonctions, vous devez choisir entre deux projets qui s’excluent mutuellement. Le projet A procure un avantage annuel de 30 000 $ et entraîne un coût annuel de 12 000 $ pendant 5 ans. Le projet B occasionne un coût de 25 000 $ la première année, puis un coût annuel de 5000 $ de la deuxième année à l’année 10. Ce projet générera par ailleurs un avantage annuel de 30 000 $ pendant 10 ans. Quel projet sélectionneriez vous en supposant un taux d’actualisation de 5 % ?
Réponse
Nous savons maintenant que la décision doit s’appuyer sur la VAN. L’énoncé ne précise pas quand les impacts se font sentir chaque année. Nous supposons un déroulement continu au cours de l’année.
Projet A
La VAN du projet A peut se calculer facilement, puisqu’il s’agit d’actualiser une annuité. En effet, l’avantage annuel net est de 8 000 $ (soit 30 000 $ – 12 000 $) pendant cinq ans. Le facteur d’annuité avec T = 5 et s = 5 % est de 4,44, de sorte que la VAN = 35 520 $.
Projet B
La valeur actualisée de l’avantage se calcule comme une annuité, avec T = 10 et s = 5 %, ce qui donne un facteur d’annuité de 7,9 et une valeur actualisée de 237 000 $.
La valeur actualisée du coût assumé au cours de la première année est de 24 398 $, soit 25 000 $/(1,05)0,5. La valeur actualisée des coûts des périodes subséquentes s’évalue comme une annuité, mais en n’oubliant pas d’actualiser la valeur obtenue, pour tenir compte du fait que l’annuité ne débute qu’à la période 2. Ainsi, la valeur actualisée de ces coûts s’élève à 35 523 $, soit (7,28 x 5 000)/(1,05)0,5.
Ainsi la valeur actualisée du projet B est de 177 079 $.
Comme les deux projets ont des horizons temporels différents, la comparaison des VAN ne peut s’effectuer directement. Nous utilisons ici la méthode par l’équivalent annuel moyen.
L’équivalent annuel moyen du projet A est de 8 000 $.
L’équivalent annuel moyen du projet B est de 22 387 $, soit 177 079/7,91 (le dénominateur correspondant au facteur d’annuité avec T = 10 et s = 5 %).
C’est donc le projet B qui doit être recommandé.
Exercices
(*) Indique que le solution est disponible
- (*) Pour mettre en œuvre un programme de maternelle pour les enfants de 4 ans, il serait nécessaire de construire de nouveaux bâtiments. On estime que le coût moyen de ces nouvelles constructions s’élèverait à 800 000 $ par classe. En supposant que la durée de vie du nouveau bâtiment serait de 40 ans et le taux d’actualisation social de 3 %, veuillez calculer le coût annuel d’une classe.
- (*) Les avantages nets des coûts d’un projet sont évalués à 450 000 $ à la fin de la première année. On estime que ces avantages nets diminueront ensuite à un taux de 2 % par année. Le projet s’étend sur 20 ans, et le taux d’actualisation social est s = 7 %. Calculez la VAN de ce projet.
- Considérez les deux projets suivants qui sont mutuellement exclusifs.
Le projet A engendre un coût de 10 millions de dollars à t = 0 et procure un avantage de 13,5 millions de dollars à t = 1 ;
Le projet B engendre également un coût de 10 millions de dollars à t = 0, mais rapporte une perpétuité de 1,08 million de dollars à partir de t = 1.
On suppose que le taux d’actualisation est de 5 %.
Montrez que l’utilisation du taux de rendement interne comme critère de décision n’aboutit pas à choisir le projet qui procure la valeur sociale la meilleure. - (*) Un projet a une durée de vie utile de 50 ans. Une ACA a évalué ses coûts et ses avantages sur un horizon de seulement 20 ans. La dernière année de cette étude estime l’avantage net courant (c’est-à-dire A-C non actualisé) à 1,5 million de dollars. Cet avantage net est positivement lié à la taille de la population touchée par le projet. On estime que durant la période de T = 21 à T = 50, le taux de croissance de la population sera de 1 % par année. Calculez la valeur résiduelle de ce projet à inclure dans l’ACA comme avantage. Le taux d’actualisation social est de 7 %.
- (*) Une municipalité enterre jusqu’à maintenant tous ses déchets dans le centre d’enfouissement d’une municipalité voisine, moyennant le paiement d’une redevance. Elle pourrait poursuivre cet arrangement, mais elle a réalisé une ACA indiquant que si elle construisait son propre site d’enfouissement, elle obtiendrait une valeur actualisée nette de 3 millions de dollars par rapport à l’option de poursuivre la solution actuelle. Le site ainsi construit aurait une durée de 15 ans. Par ailleurs, la municipalité pourrait construire à la fois un site d’enfouissement et un centre de compostage. La valeur actualisée nette de cette option a été évaluée à 4 millions de dollars. Dans cette alternative, elle pourrait se défaire de ses déchets pendant 30 ans. En vous appuyant sur les informations fournies et en supposant un taux d’actualisation social de 5 %, quelle option recommanderiez vous ?
Bibliographie
Baldwin J., Liu, H. et Tanguay, M. (2015). Une mise à jour des taux d’amortissement pour les Comptes canadiens de productivité, La revue canadienne de productivité, (39). Statistique Canada. https://www150.statcan.gc.ca/n1/pub/15-206-x/15-206-x2015039-fra.htm
Boardman A. E., Greenberg, D. H., Vining, A. R. et Weimer, D. L. (2018). Chapter 9: Discounting Future Impacts and Handling Inflation. In Cost-benefit analysis: concepts and practice (5th ed.). University of British Columbia. https://doi.org/10.1017/9781108235594
Fraumeni, B. M. (1997). The Measurement of Depreciation in the U.S. National Income and Product Accounts. Survey of current business, (July), 7-23. https://apps.bea.gov/scb/pdf/national/niparel/1997/0797fr.pdf
Jenkins, G. P., Kuo C.-H. et Harberger, A. C. (2011). Chapter 4: Discounting and Alternative Investment Criteria. In Cost-Benefit Analysis for Investment Decisions (1-30). https://agrilinks.org/sites/default/files/resource/files/cost-benefit_analysis_for_investment_decisions.pdf
Patry, A. (2007). Economic Depreciation and Retirement of Canadian Assets: A Comprehensive Empirical Study (15-549-XIE), Statistics Canada. https://www150.statcan.gc.ca/n1/en/pub/15-549-x/15-549-x2007001-eng.pdf?st=bkcLlRRq
Régie de l’énergie. (2024). Prix de l’essence ordinaire – Par région administrative. https://www.regie-energie.qc.ca/fr/consommateurs/informations-pratiques/essence-ordinaire-par-region-administrative-du-quebec#prix-moyen-releve-hebdomadaire
Sliker, B. K. (2018). Implications of Geometric Cohort Depreciation for Service-Life Distributions, Bureau of Economic Analysis (September), 1-33. https://www.bea.gov/system/files/papers/Revised%20Geo%20Depr%20Gamma%20Lifespans.pdf
Statistique Canada. (2024). Indice des prix à la consommation, moyenne annuelle, non désaisonnalisé (Tableau 18-10-0005-01). https://www150.statcan.gc.ca/t1/tbl1/fr/tv.action?pid=1810000501
- L’inverse peut également arriver. Par exemple, l’exploitation d’une centrale nucléaire peut produire des avantages aujourd’hui, mais qui entraînent des coûts environnementaux et de traitement des déchets qui sont reportés dans l’avenir. ↵
- L’impact de la périodicité de l’actualisation sur les résultats est faible, particulièrement par rapport au degré de précision qu’on peut atteindre dans une ACA. Par exemple, un million reçu dans dix ans vaut aujourd’hui 613 913 $, lorsqu’on actualise sur une base annuelle à un taux de 5 %. Si l’actualisation se fait de manière continue (c’est-à-dire si les intérêts sont calculés de manière continue), on parvient à un montant de 606 530 $, soit une variation de moins de 3 %. ↵
- Pour les États-Unis, voir Fraumeni (1997) et Sliker (2018). Pour le Canada, Baldwin J., H. Liu et M. Tanguay (2015). ↵
- Le US Bureau of Economic Analysis détermine le taux de dépréciation géométrique δ par le ratio du taux d’amortissement dégressif (TAD) et la durée de vie de l’actif (T), soit δ=(TAD/T) . Cet organisme utilise une valeur générique de 1,65, sauf pour les actifs gouvernementaux pour lesquels la valeur de 0,91 est utilisée. ↵
- La synergie pourrait être négative. Elle pourrait aussi se produire du côté des coûts. ↵
- Notons que la dépréciation comptable ne représente pas toujours adéquatement la dépréciation économique d’un actif. ↵
- Avec l’approche 1, il faudra inclure le coût d’usage durant la période d’analyse de cinq ans. En revanche, l’approche 2 sous-évalue le coût de l’actif, si l’on ne prend en compte que le loyer des cinq premières années. ↵
Valeur qu’une ressource aurait pu fournir dans son meilleur usage alternatif.
Situation servant à déterminer l’impact d’un projet au moyen de l’évolution de l’avantage social net de ce scénario. Il s’agit en général du statu quo, soit la situation sans le projet, ce qui n’est pas pour autant une situation « à coût nul » et ne veut pas forcément dire « ne rien faire ».
Durée pendant laquelle les coûts et les avantages d’un projet sont comptabilisés. Il s’agit souvent d’une question complexe à laquelle se mêlent des considérations d’ordres technique et pragmatique. Généralement, adopter un horizon court assure une meilleure fiabilité des prévisions, mais avec le risque d’ignorer les effets à plus long terme.
L’analyse coûts-avantages représente un cadre méthodologique issu de la théorie économique et destiné à évaluer la rentabilité sociale d’un projet en évaluant en unités monétaires la somme des coûts et des avantages de l’ensemble des membres d’une société de référence. Cette analyse est dite « partielle », car elle se concentre sur les impacts d’un projet sur un nombre limité de marchés. L’ACA est applicable à une large gamme de projets, comprenant les infrastructures, les politiques publiques ainsi que les initiatives privées. Elle est particulièrement pertinente lorsqu’il existe une suspicion de divergence entre la rentabilité sociale et la rentabilité privée d’un projet.
Étude de l’évolution de la valeur actualisée nette lors de changements des paramètres et des prévisions. Il existe trois types d’analyse de sensibilité : par paramètre, par scénario et par simulation de Monte-Carlo.
Établit dans quelle mesure les avantages sociaux d’un projet excèdent les coûts sociaux.
Montant maximum que les bénéficiaires d’un projet sont prêts à débourser pour en profiter, ou que les victimes d’une nuisance consentent à payer pour l’éviter. Dans certaines situations, le CAP peut s’observer sur les marchés par les comportements d’achat. En revanche, dans d’autres situations où il n’existe pas de marché, il est nécessaire de recourir à des techniques particulières pour l’évaluer.
Outil d’évaluation économique d’un projet alternatif à l’ACA.
Elle consiste à calculer les entrées, les sorties et les besoins de financement pendant la durée du projet ; établir son montage financier, c’est-à-dire déterminer les modes de financement (emprunts, émissions d’obligations) et répartir les responsabilités entre les partenaires.
Il ne s’agit donc pas d’une évaluation des coûts et des avantages sociaux du projet, mais plutôt des coûts et des avantages financiers des partenaires. Cette analyse sert notamment à évaluer la rentabilité privée du projet pour ses partenaires. Les données produites dans le cadre d’une analyse financière sont souvent très utiles pour la réalisation d’une ACA.
Rapport entre le coût total et le nombre d’unités produites.

