20 Les autres méthodes d’évaluation de projets
La motivation et les objectifs d’apprentissage

Dans les années 1970, les Forces armées des États-Unis ont identifié le besoin d’avoir un avion-cargo capable de transporter de lourds équipements sur de longues distances, tout en étant en mesure d’atterrir dans des conditions difficiles. Au début des années 1980, la proposition de McDonnell Douglas (désormais Boeing) pour le développement de l’avion C-17 Globemaster a été retenue, avec un plan initial de livraison de 120 appareils. Cependant, le développement de cet avion a rencontré divers problèmes, notamment des dépassements de coûts, ce qui a conduit le Congrès américain, en 1993, à exiger une analyse indépendante pour déterminer si le programme C-17 devait être poursuivi ou si des alternatives allaient être plus appropriées. Comment aborder cette évaluation ? Une analyse coût-avantage est particulièrement difficile dans ce contexte, puisque la mesure et la valorisation des avantages posent des défis majeurs. Comment peut-on établir un lien de causalité clair entre l’achat de matériel militaire et l’amélioration de la sécurité nationale ? Quelle valeur accorder à une réduction des risques d’attaque et à l’accroissement du sentiment de sécurité ?
Dans ce chapitre, nous explorons trois approches alternatives à l’ACA, déjà brièvement présentées au chapitre 1. Ce chapitre offre un aperçu général de ces méthodes et renvoie à des références, afin d’approfondir leur compréhension.
À la fin de ce chapitre, vous serez en mesure de :
1. Comprendre la mécanique et les limites de l’analyse des impacts économiques ;
2. Décrire les principes et les étapes nécessaires pour mener une analyse coût-efficacité ;
3. Expliquer les notions clés de l’analyse coût-utilité.
20.1 Les analyses d’impacts économiques
Pour débuter cette section, rappelons certains éléments abordés dans le chapitre 1 concernant l’analyse d’impacts économiques.
L’analyse d’impacts économiques (Economic Impact Analysis) est un ensemble de techniques s’appuyant sur des modèles input-output visant à évaluer les effets ou les retombées économiques d’un projet. Ces effets peuvent être mesurés en termes d’emplois, de valeur ajoutée, de recettes fiscales ou d’importations.
Cependant, cette approche ne permet pas de déterminer la rentabilité sociale d’un projet, et ce, pour deux raisons principales :
- La non-additivité des impacts économiques : Les impacts économiques mesurés par cette approche ne sont souvent pas additionnels, puisque les fonds investis dans un projet pourraient l’être dans un autre projet qui engendrerait lui aussi des retombées économiques. En d’autres termes, les retombées peuvent être associées à des redéploiements d’activités existantes plutôt qu’à des gains nets pour l’économie[1];
- L’absence de mesure des avantages nets : L’analyse d’impacts économiques ne mesure pas les avantages nets d’un projet, c’est-à-dire la différence entre les avantages et les coûts sociaux du projet. Un projet peut donc générer des retombées économiques significatives, tout en présentant une rentabilité sociale négative.
Bien que l’analyse des impacts économiques ne puisse déterminer la rentabilité sociale d’un projet, elle demeure populaire auprès des décideurs, car elle garantit des résultats positifs, notamment en matière de création ou de maintien d’emplois ainsi que de retombées fiscales. Il est donc essentiel de comprendre davantage la mécanique de cette approche et de rappeler ses limites.
20.1.1 La mécanique des impacts économiques [2]
Un projet peut s’analyser comme constituant un choc positif de la demande auprès des fournisseurs directs. Par exemple, la construction d’une nouvelle autoroute augmentera la demande dans le secteur de la construction et du génie civil d’un milliard de dollars. Dans le cadre des analyses d’impacts, les dépenses auprès des fournisseurs directs sont appelées effets directs. Ces dépenses peuvent être décomposées en plusieurs catégories :
- L’achats de biens et services intermédiaires : Pour réaliser l’autoroute, le secteur de la construction et du génie civil devra acheter du bitume, de l’acier et autres services de soutien auprès de fournisseurs directs, appelés premiers fournisseurs.
- Les importations (fuites) : Une partie des dépenses des fournisseurs directs sera consacrée à l’achat de biens et services intermédiaires importés, comme un camion acheté à l’étranger. Ces importations représentent des « fuites » pour l’économie nationale, car cet argent sort du pays et ne génère pas d’impacts supplémentaires.
- Les taxes : Une partie des dépenses du projet sera versée sous forme de taxes et de redevances aux gouvernements.
- La valeur ajoutée : Une partie de l’effet direct se traduit par la valeur ajoutée générée par les fournisseurs directs. La valeur ajoutée est définie comme la différence entre les revenus tirés des ventes et les dépenses en consommation intermédiaire (y compris les fuites et les taxes). Ce solde mesure donc la valeur créée par les fournisseurs, grâce à l’utilisation des facteurs de production primaires, du capital et du travail. En d’autres termes, la valeur ajoutée permet de rémunérer le facteur travail ainsi que le capital.
Cette décomposition des effets directs chez les fournisseurs est illustrée dans la Figure 1. Par définition, ces effets directs correspondent au coût total du projet, soit un milliard de dollars dans notre exemple.
La composante « achats de biens et services intermédiaires par les fournisseurs directs » représente un choc de demande pour les premiers fournisseurs. Ce choc se décompose à son tour en fuites, taxes, valeur ajoutée et achats de biens et services intermédiaires auprès des deuxièmes fournisseurs. Ce processus se poursuit à chaque niveau de la chaîne de production, comme l’illustre le schéma ci-dessous. Ces effets cumulés sont appelés effets indirects[3], reflétant les impacts sur les fournisseurs tout au long des différentes étapes de production du projet.
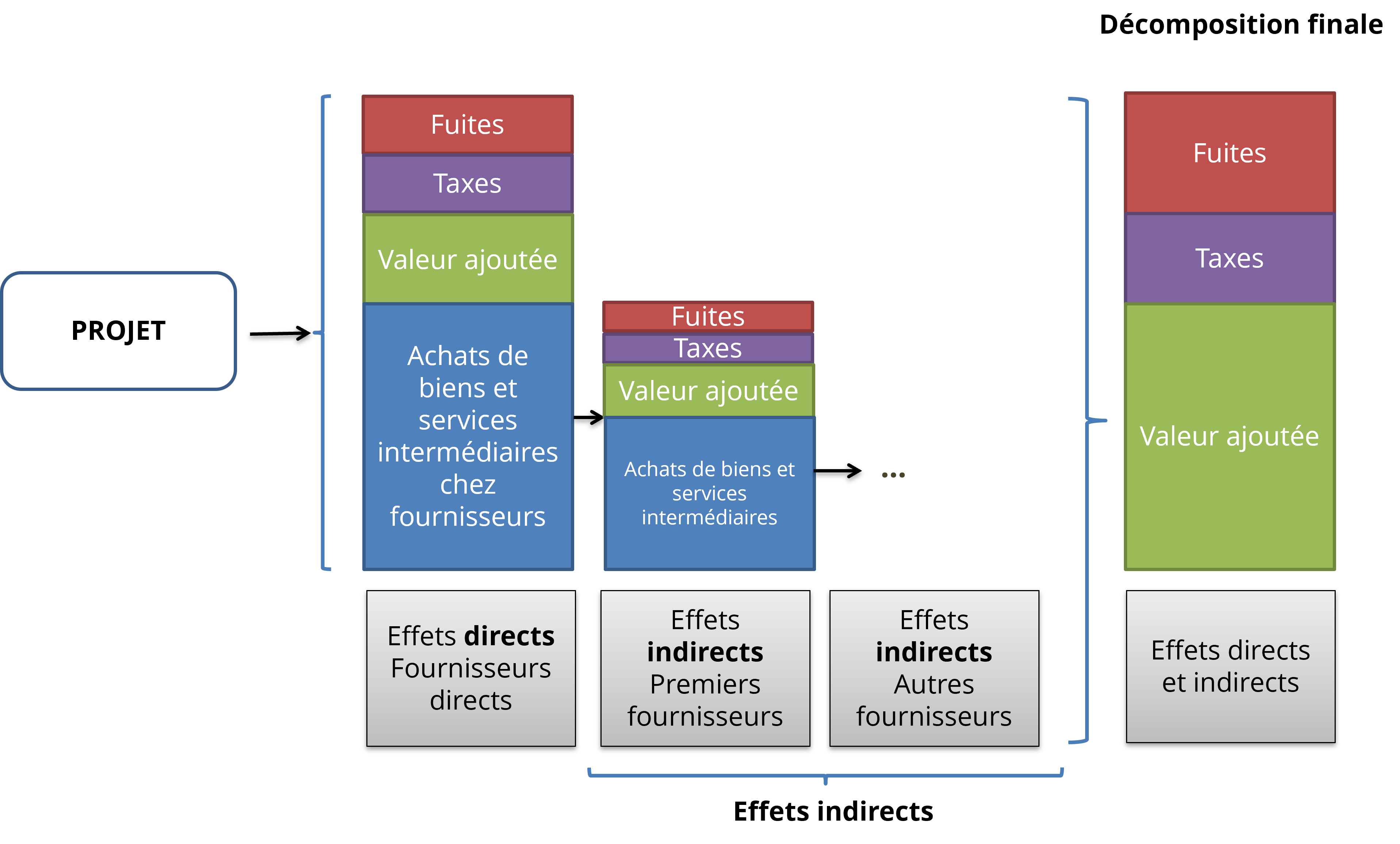
À partir de ce processus, il est donc possible de traduire le choc initial en fuites, en taxes et en valeur ajoutée, comme l’illustre la décomposition finale à la Figure 1. On constate qu’un projet d’un milliard de dollars engendrera une valeur ajoutée inférieure à un milliard de dollars, en raison des fuites (importations et épargne) et des taxes.
Pour obtenir des retombées économiques plus importantes, il est nécessaire de considérer les effets induits. Comme l’illustre la Figure 2, la valeur ajoutée générée par un projet représente des revenus pour les facteurs de production primaires, à savoir le capital et le travail. Une partie de ces revenus sera épargnée, ce qui constitue une autre fuite pour l’économie courante, mais une autre partie sera dépensée dans divers secteurs de l’économie. Par exemple, un ouvrier travaillant sur le chantier de l’autoroute pourrait utiliser son revenu pour acheter des produits alimentaires, une nouvelle télévision ou des services de garde. Ces dépenses supplémentaires stimulent ainsi la demande dans ces secteurs, générant des revenus qui seront à leur tour dépensés, amplifiant l’impact initial du projet. Ces dynamiques sont connues sous le nom d’effets multiplicateurs.

C’est donc grâce aux effets induits que les impacts économiques peuvent dépasser le montant initial investi dans le projet. Les partisans du projet de construction de l’autoroute utilisent souvent des formulations telles que : « Chaque dollar investi dans l’autoroute générera plus de deux dollars en retombées économiques. »
20.1.2 Les limites des analyses des retombées
Les principales limites de cette approche sont les suivantes (voir aussi Gunton et al., 2020) :
- L’incapacité à sélectionner les projets : Tous les projets, même les moins désirables sur le plan social, génèrent des retombées économiques positives. Cela peut inciter à privilégier le projet qui, à taille égale, offre les retombées économiques les plus importantes (par exemple, la plus grande valeur ajoutée ou les retombées fiscales les plus élevées). Cette approche tend à favoriser les projets issus de secteurs présentant moins de fuites et des multiplicateurs plus élevés. Bien que cela puisse s’avérer justifiable dans une optique de stabilisation économique en période de récession, il est important de considérer également les coûts d’opportunité liés au financement du projet (comme les impacts économiques négatifs découlant des taxes nécessaires pour le financer). Mais, ce mode de sélection n’assure pas que le projet choisi sera socialement rentable, puisque les retombées ne mesurent pas les avantages sociaux, comme nous l’avons mentionné dans l’introduction de cette section ;
- L’absence d’effets sur les prix : Les impacts économiques sont souvent calculés à l’aide de modèles entrées-sorties (input-output) s’appuyant sur l’hypothèse d’une sous-utilisation généralisée des facteurs de production. Dans ce cadre, un projet stimulant la demande n’a pas d’effet sur les prix (les courbes de l’offre étant supposées parfaitement élastiques) et, par conséquent, n’a aucun effet d’éviction. Toutefois, dans une économie en situation de plein emploi, un choc positif de la demande risque de provoquer une hausse des prix, entraînant un déplacement de l’activité d’un secteur à un autre, plutôt qu’une augmentation de l’activité globale. En négligeant cet aspect, les retombées économiques sont surestimées.
- Des relations statiques : Les études d’impacts économiques supposent que les relations entre secteurs sont fixes et ne sont pas influencées par le projet, ce qui peut s’avérer limitatif. Par exemple, un projet favorisant l’automatisation dans un secteur pourrait modifier la quantité de la main-d’œuvre requise, entraînant ainsi des effets sur les interrelations économiques.
- La validité des multiplicateurs : Les effets induits sont parfois évalués en utilisant des multiplicateurs dont la validité est discutable. Il est également important de noter que, dans le cadre d’une analyse des retombées au niveau local ou régional, les effets induits sont souvent limités. En effet, toute dépense réalisée à l’extérieur de l’économie locale ou régionale est considérée comme une fuite, réduisant ainsi la possibilité d’effets induits significatifs.
Le modèle intersectoriel du Québec
Au Québec, l’Institut de la statistique du Québec a développé le Modèle intersectoriel du Québec (MISQ), un modèle de type input-output. Celui-ci divise l’économie québécoise en 184 secteurs productifs, 447 catégories de biens et services et 240 secteurs de la demande finale. Ce modèle permet de calculer les effets directs et indirects, mais non les effets induits. Ainsi, un choc de 100 millions de dollars sur la demande aura des retombées économiques inférieures à 100 millions de dollars, en raison des fuites. Pour plus de détails sur ce modèle, il est recommandé de consulter l’Institut de la statistique du Québec (2023). Les effets induits sont parfois ajoutés à l’analyse d’un projet par des analystes qui utilisent des multiplicateurs sectoriels spécifiques.
20.2 L’analyse coût-efficacité
20.2.1 Les principes de base
L’analyse coût-efficacité (ACE) compare des projets en calculant le ratio entre le coût total du projet (C) et une mesure de son efficacité (E), soit C/E. Le coût est exprimé en unités monétaires, tandis que l’efficacité est évaluée en unités « physiques », comme le nombre de vies sauvées dans les projets de sécurité routière. Ce ratio se traduit par le coût par unité d’impact, par exemple, le coût par vie sauvée.
L’ACE mesure ces coûts et cette efficacité par rapport à une situation de référence qui varie selon le contexte de l’analyse. Le terme différentiel est donc souvent ajouté pour préciser qu’on examine les variations de coûts et d’efficacité par rapport à une situation de référence.
Contrairement à l’ACA, l’ACE ne cherche pas à valoriser tous les avantages d’un projet. Elle est donc particulièrement adaptée pour comparer des projets ayant un avantage principal similaire.
L’analyse peut également être réalisée en utilisant le ratio inverse, E/C, qu’on appelle « analyse efficacité-coût ». Ce ratio E/C mesure l’impact du projet par dollar investi. Dans ce chapitre, nous nous concentrons sur l’analyse coût-efficacité, bien que les concepts s’appliquent également à l’analyse efficacité-coût.
Le Tableau 1 présente un exemple fictif d’initiatives visant à réduire la consommation d’eau des ménages dans une région aride. Les initiatives sont classées par ordre croissant de coût total, et la situation de référence est l’absence de mesure (ne rien faire). Le tableau comprend l’estimation du coût incrémental annuel de chaque mesure, les économies d’eau incrémentales et les ratios coût-efficacité incrémentaux.
L’analyse montre que l’installation de réducteurs de débit sur les robinets constitue la mesure la plus économique par mètre cube d’eau économisé, suivie de l’installation de pommeaux de douche économes et de chasses d’eau à double commande. En revanche, l’installation de récupérateurs d’eau de pluie est beaucoup plus coûteuse par mètre cube d’eau économisé.
| Mesure | Coût incrémental estimé* ($/an) |
Économie d’eau incrémentale estimée* (m3/an) |
Ratio coût-efficacité incrémental* ($/m3) |
| A- Réducteur de débit des robinets | 1 200 000 | 23 000 000 | 0.052 |
| B- Installation de pommeaux de douche économes | 1 345 000 | 14 560 000 | 0,092 |
| C- Chasse d’eau à double commande | 1 660 000 | 16 450 000 | 0.1 |
| D- Récupérateur d’eau de pluie | 17 300 000 | 6 520 000 | 2,65 |
* Évalué relativement à une situation de référence dans laquelle aucune mesure n’est prise.
L’ACE est utilisée dans divers domaines, notamment en éducation pour comparer des initiatives visant à améliorer les scores d’apprentissage (Yeh, 2010 ; McEwan, 2012), en santé et sécurité pour évaluer des mesures visant à sauver des vies (Vahidnia et Walsh, 2002) ainsi que dans le secteur de l’énergie pour analyser des programmes d’efficacité énergétique (Tuominen et al., 2015).
Les avantages et les limites
L’ACE offre l’avantage d’être moins contraignante que l’analyse coûts-avantages (ACA), car elle n’exige pas de valoriser tous les avantages d’un projet. Elle se concentre sur la quantification d’un seul effet, sans avoir à lui attribuer une valeur monétaire. Cela s’avère particulièrement utile lorsque les autres effets du projet sont diffus ou difficiles à mesurer. Par exemple, si des mesures de santé réduisent les risques de complications chirurgicales, il est plus simple de mesurer l’efficacité en termes de jours d’hospitalisation évités plutôt que de tenter de quantifier tous les bénéfices possibles. Toutefois, certains avantages peuvent être ignorés.
Un autre atout de l’ACE réside dans le fait qu’elle évite certaines controverses éthiques, notamment celles liées à la monétisation d’effets intangibles, comme la valeur d’une vie humaine. Cependant, cela ne résout pas entièrement le problème, car le décideur devra finalement se prononcer sur la rentabilité des résultats obtenus. Par exemple, faut-il entreprendre un projet qui coûte 15 millions de dollars par vie sauvée ? Ainsi, même si l’ACE simplifie certains aspects, elle ne permet pas d’échapper à ces dilemmes délicats.
Une autre limite de cette approche veut que sélectionner un projet uniquement sur la base du ratio coût-efficacité incrémental n’assure pas forcément le choix du projet qui maximise la rentabilité sociale (voir la section 20.3.3).
20.2.2 La réalisation d’une ACE
Schématiquement, la réalisation d’une ACE comprend quatre étapes :
- 1. Établir la liste des projets qui seront comparés ;
- 2. Estimer le coût et l’efficacité de chaque mesure ;
- 3. Calculer les ratios coûts-efficacité différentiels pertinents ;
- 4. Comparer et sélectionner les projets.
L’étape 1 dépend du contexte et de l’objectif, de sorte qu’il est difficile d’en dire davantage.
L’étape 2 : Estimer le coût et l’efficacité de chaque mesure
La détermination du coût doit idéalement suivre les mêmes principes que pour l’ACA :
- Les coûts sont évalués sur la base de la notion de renonciation ;
- Le coût total d’une mesure doit idéalement correspondre à la somme des coûts pour l’ensemble des parties prenantes de la société de référence, soit le coût social ;
- Les coûts doivent être actualisés avant d’être additionnés, afin d’obtenir le coût total en valeur monétaire de l’année de référence.
Cependant, il est courant, dans la pratique, que les coûts soient définis de manière plus étroite, en ne considérant que les coûts pour la partie qui a commandé l’analyse. Par exemple, une ACE de programmes publics d’efficacité énergétique ne prendra en compte que les coûts pour l’État. Cette pratique devrait être évitée ou, à tout le moins, des mises en garde devraient être ajoutées lorsque les recommandations sont émises.
La mesure de l’efficacité doit cibler l’avantage principal recherché. Comme nous l’avons mentionné précédemment, l’ACE est particulièrement adaptée à la comparaison de projets qui engendrent un même avantage principal.
Bien que l’efficacité soit mesurée en unités physiques, les effets qui s’étendent sur plusieurs années doivent être additionnés après avoir été actualisés. Par exemple, un projet qui sauve 10 vies par année pendant cinq ans n’a pas la même efficacité qu’un programme qui sauve 50 vies immédiatement. L’ACE désigne ce processus sous le nom de « principe d’actualisation des conséquences », qui permet de comparer des effets différés dans le temps, en tenant compte de leur valeur moindre à l’avenir.
L’étape 3 : Calculer les ratios coûts-efficacité
Tel que mentionné précédemment, l’ACE compare les coûts et l’efficacité différentiels par rapport à une situation de référence, qui peut varier selon le contexte. On parle alors du ratio coûts-efficacité différentiel (RCED) du projet j par rapport au projet i. Cependant, nous utiliserons l’abréviation anglaise ICER (Incremental Cost-Effectiveness Ratio) dans la suite, car elle est couramment employée, même dans des rapports en français.
Le ICER d’un projet j relativement à un projet i se définit comme suit :
[latex]ICER = \frac{\Delta C}{\Delta E} = \frac{C_j - C_i}{E_j - E_i}[/latex]
où [latex]C_j[/latex] et [latex]C_i[/latex] représentent les coûts des projets, [latex]j[/latex] et [latex]i[/latex] et [latex]E_j[/latex], [latex]E_i[/latex] les mesures de l’efficacité des deux projets.
Le numérateur et le dénominateur peuvent s’avérer positifs ou négatifs, suivant le contexte. Dans une perspective d’amélioration des services, on examinera des projets qui coûtent plus ( [latex]\Delta C[/latex]> 0), mais qui améliorent aussi l’efficacité ([latex]\Delta E[/latex]> 0). Dans une perspective de restriction budgétaire, il peut devenir nécessaire de trouver une alternative qui coûte moins cher ([latex]\Delta C[/latex] < 0), en causant le moins d’impacts sur l’efficacité ([latex]\Delta E[/latex]< 0). Il est parfois aussi possible de réduire les coûts ([latex]\Delta C[/latex] < 0), tout en améliorant l’efficacité ([latex]\Delta E[/latex] > 0), et l’inverse est également possible ( [latex]\Delta C[/latex]> 0 et [latex]\Delta E[/latex] < 0).
Si le projet j est comparé à la situation « aucun projet », alors [latex]C_i[/latex] = 0 et [latex]E_i[/latex] = 0, de sorte que le ICER devient [latex]\frac{C_j}{E_j}[/latex]. Ce ratio particulier est parfois nommé « le ratio coût-efficacité moyen ».
Exemple : De nouveaux traitements contre la malaria
Une entreprise pharmaceutique a créé un nouveau médicament et un vaccin pour prévenir la malaria chez les populations à très haut risque[4]. Elle souhaiterait savoir si le nouveau médicament ou le vaccin pourraient remplacer efficacement le traitement actuel. Les méthodes de prévention de la malaria ne peuvent être prises conjointement, car leur combinaison causerait trop d’effets secondaires. Les projets sont donc mutuellement exclusifs. On s’intéresse ainsi aux coûts et à l’efficacité des deux nouvelles options par rapport au traitement actuel. Le Tableau 2 présente les trois options thérapeutiques par ordre croissant des coûts.
| Projet | Coût ($/année) | Coût différentiel* | Efficacité | Efficacité différentielle* | ICER* |
| A – Traitement actuel | 350 $ | – | 90 % | – | – |
| B-Nouveau médicament | 500 $ | 150 $ | 96 % | 6 % | 2500 $ |
| C- Vaccin | 620 $ | 270 $ | 99 % | 9 % | 3000 $ |
La colonne 2 du Tableau 2 montre le coût annuel par personne de chaque option, tandis que la colonne 3 correspond au coût additionnel des nouvelles options par rapport au traitement actuel A. Le nouveau médicament B coûte 150 $ de plus par personne, tandis que le vaccin coûte 270 $ de plus que le traitement actuel. La colonne 4 montre l’efficacité de chaque option par rapport à l’absence complète de traitement, et la colonne 5 calcule l’efficacité différentielle des nouveaux traitements par rapport au traitement actuel. On constate, par exemple, que le vaccin améliore l’efficacité de 9 %, et le nouveau médicament de 6 %. Enfin la dernière colonne calcule le ICER, soit les ratios de la colonne 3 et de la colonne 5.
Dans cet exemple, ce ratio s’interprète comme le coût par cas évité de plus par rapport au traitement initial, soit 2500 $ pour le nouveau médicament et 3000 $ pour le vaccin. En effet, sur une population de 100 personnes, 10 seront atteintes de la malaria si on utilise le traitement A, et 4 avec le traitement B. Les coûts totaux sont respectivement de 35 000 $ et de 50 000 $. Ainsi, le traitement B évite la maladie à 6 personnes de plus que le traitement initial, pour un coût additionnel de 15 000 $, ce qui donne bien un coût par cas additionnel évité de 2500 $.
Exercice
Déterminez le ICER du vaccin C par rapport au nouveau médicament B. Discutez de l’interprétation de ce ratio.
Résolution
Le ICER de C par rapport à B est de 120 $ / 0,03 = 4 000 $. Ce montant représente le coût par cas additionnel évité du traitement C par rapport au traitement B. On constate donc une augmentation du coût additionnel plus l’efficacité augmente. Il s’agit d’une autre illustration d’une réalité omniprésente, celle de l’accroissement des coûts marginaux.
Étape 4 : Comparer et sélectionner les projets[5]
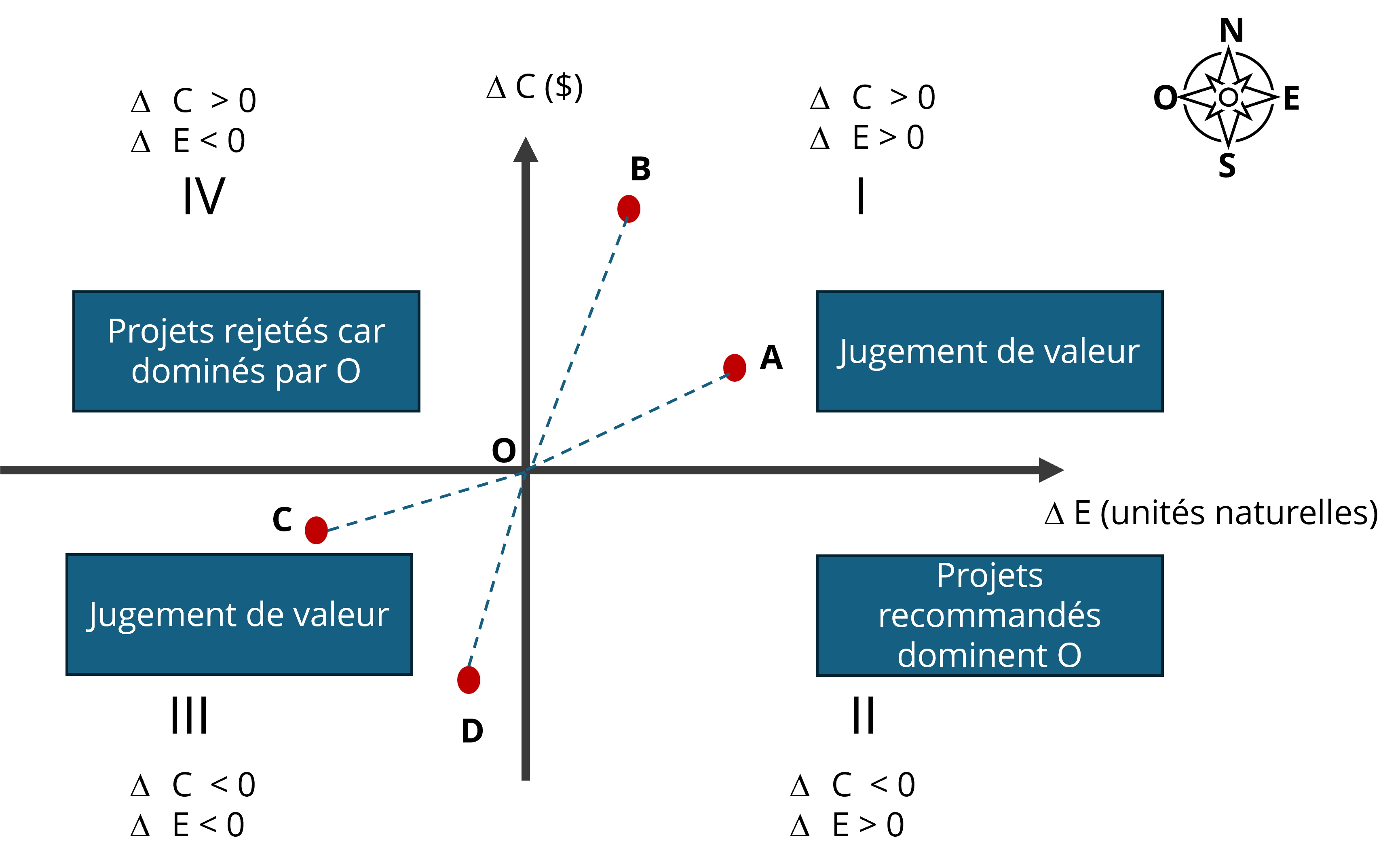
Comment établir des recommandations à partir d’une ACE ? Il est utile de représenter graphiquement les situations possibles dans le plan coûts-efficacité. Dans la Figure 3, l’axe horizontal mesure le différentiel d’efficacité, et l’axe vertical mesure le différentiel des coûts par rapport à la situation de référence, représentée par le point O sur le graphique. Les points (A, B, C et D) représentent les projets à l’étude.
La pente de la droite liant l’origine à un projet correspond par définition à l’ICER de ce projet par rapport à la situation de référence O. En effet, la pente correspond à [latex]\frac{\Delta C}{\Delta E}[/latex].
La Figure 3 permet de distinguer quatre quadrants qui influencent les règles de sélection des projets :
- Quadrant I (Nord-Est): Les projets améliorent l’efficacité, mais à un coût additionnel ( > 0 et > 0). Le processus de recommandation nécessite un jugement de valeur, c’est-à-dire de déterminer un seuil critique correspondant au montant maximal qu’on est prêt à payer par unité d’efficacité additionnelle. Des contraintes budgétaires peuvent également être déterminantes.
- Quadrant II (Sud-Est) : Les projets réduisent les coûts (< 0), tout en améliorant l’efficacité (> 0). Ces options sont dominantes et améliorent la situation par rapport au statu quo. Le choix final dépendra du contexte, comme nous le verrons par la suite dans cette section.
- Quadrant III (Sud-Ouest): Les projets réduisent les coûts < 0), mais au détriment de l’efficacité (< 0). La sélection des projets dans ce quadrant doit s’appuyer sur un jugement de valeur, c’est-à-dire sur un seuil critique correspondant à la réduction minimale des coûts exigée pour accepter de subir une réduction de l’efficacité. Les impacts budgétaires peuvent également intervenir.
- Quadrant IV (Nord-Ouest): Les projets augmentent les coûts ( > 0), tout en réduisant l’efficacité ( < 0). Ces projets sont dominés par le statu quo et ils doivent être rejetés.
Dans les quadrants I et III, une fois fixé le seuil critique des coûts-efficacité, également appelé seuil maximal de propension à payer, il est possible d’éliminer les projets qui ne respectent pas ce seuil. Graphiquement, il s’agit de tracer une droite passant par l’origine, et dont la pente correspond au seuil critique (voir la Figure 4). Les projets situés au-dessus de cette droite ont un ICER supérieur au seuil et doivent donc être rejetés, tandis que les projets placés en dessous de cette droite doivent continuer à être pris en considération. Il est important de noter que ces recommandations sont effectuées en comparant les projets à la situation de référence représentée par le point O. Pour aller plus loin, la comparaison entre projets peut s’avérer nécessaire, comme nous le verrons ci-dessous.
Exercice
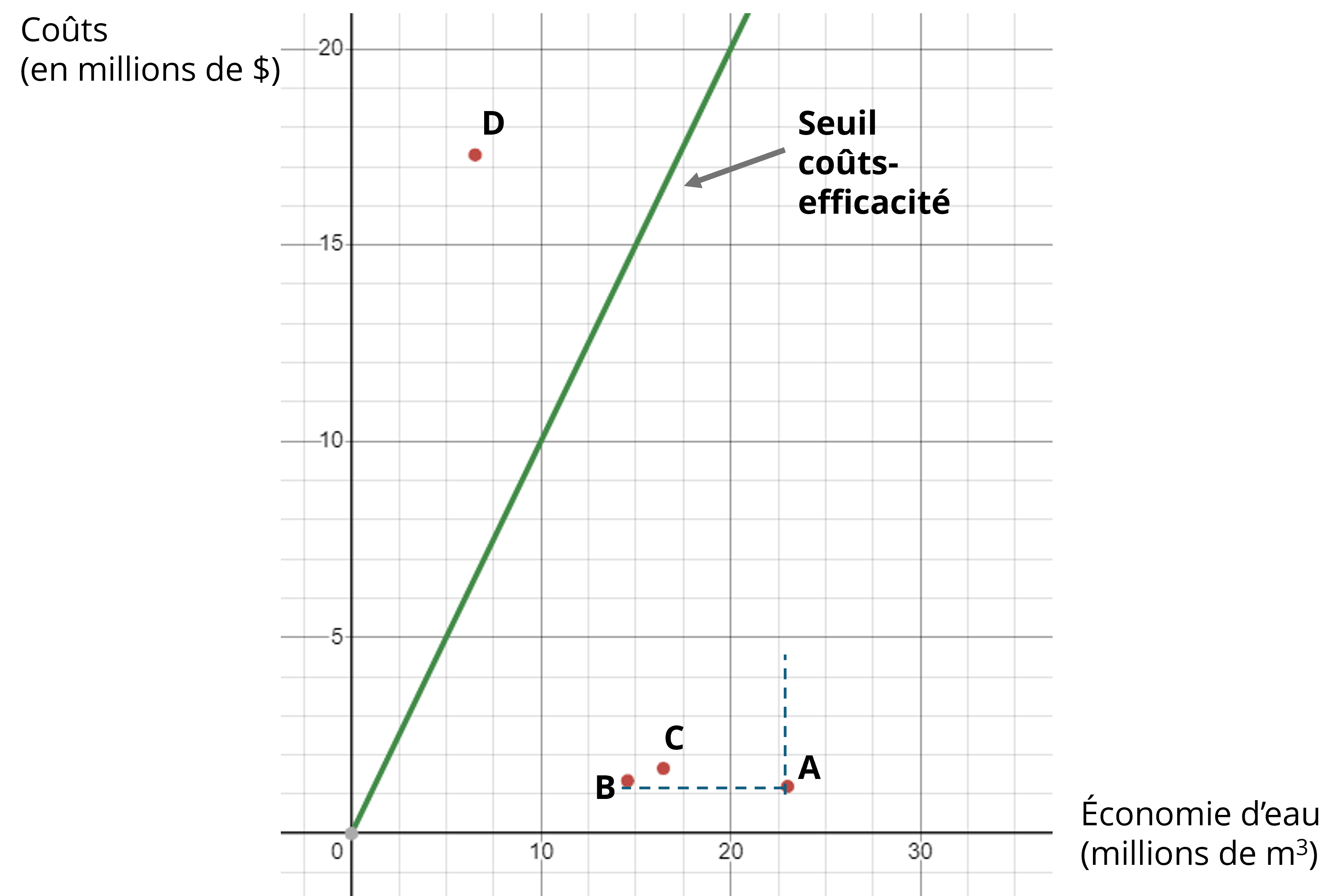
Revenons à l’exemple des mesures d’économie d’eau présenté à la section 20.2.1. Le Tableau 3 reprend les données sur l’efficacité-coûts de ces mesures. Représentez dans le plan coûts-efficacité les projets contenus dans ce tableau, en utilisant l’absence de mesure d’économie d’eau comme situation de référence. Représentez également le seuil critique coûts-efficacité, en supposant que le montant maximal acceptable par la municipalité a été fixé à 1 $/m³. En tenant pour acquis que ces projets ne sont pas mutuellement exclusifs, quelle sera votre recommandation ?
| Mesure | Coût incrémental estimé* ($/an) |
Économie d’eau incrémentale estimée* (m3/an) |
Ratio coûts-efficacité incrémentaux* ($/m3) |
| A- Réducteur de débit des robinets | 1 200 000 | 23 000 000 | 0.052 |
| B- Installation de pommeau de douche économe | 1 345 000 | 14 560 000 | 0,092 |
| C- Chasse d’eau à double commande | 1 660 000 | 16 450 000 | 0.1 |
| D- Récupérateur d’eau de pluie | 17 300 000 | 6 520 000 | 2,65 |
* Évalué relativement à une situation de référence pour laquelle aucune mesure n’est prise.
Résolution
Tous les projets améliorent l’efficacité, mais entraînent des coûts additionnels, de sorte qu’ils sont tous situés dans le quadrant I. La Figure 4 illustre ces mesures dans le plan coûts-efficacité ainsi que le seuil coûts-efficacité représenté par une droite dont la pente est de 1. Comme ces projets ne sont pas mutuellement exclusifs, les mesures A, B et C sont à recommander, mais la mesure D doit être rejetée.
Concernant le cas des projets qui sont mutuellement exclusifs, une analyse séquentielle permet d’affiner les recommandations.
L’analyse séquentielle de projets mutuellement exclusifs
Lorsque les projets sont mutuellement exclusifs, ils doivent être comparés, non seulement au statu quo, mais également entre eux. Pour cela, les projets doivent d’abord être classés par ordre croissant de coût total.
Il est ensuite possible d’éliminer certains projets, parce qu’ils sont dominés par d’autres projets. On distingue la dominance forte de la dominance faible (ou par extension).
La dominance forte
Le projet i est fortement dominé par le projet j si [latex]C_i[/latex]≥ [latex]C_j[/latex]et [latex]E_i[/latex]≤ [latex]E_j[/latex] avec au moins une inégalité stricte. On dit aussi que [latex]j[/latex] domine strictement [latex]i[/latex].
La dominance stricte va également se traduire par un ICER de [latex]j[/latex] par rapport à [latex]i[/latex], qui est négatif ou non défini.
Les projets mutuellement exclusifs qui sont strictement dominés doivent être rejetés.
Le projet i ne doit jamais être choisi, puisqu’il coûte plus cher que le projet j, avec une efficacité qui n’est pas meilleure ou il ne coûte pas moins cher, mais présente une efficacité strictement moindre que le projet j.
Soulignons qu’un ICER négatif peut indiquer non seulement qu’un projet est dominé, mais également qu’un projet est dominant. Prenons un exemple concret : le projet A génère un coût de 3 000 $ par rapport à l’option de ne rien faire, pour une efficacité incrémentale de 100. En revanche, le projet B coûte 2 000 $ pour atteindre une efficacité de 150 par rapport à ne rien faire. En calculant l’ICER de B par rapport à A, nous obtenons -1/2, soit -1 000/50. Dans ce cas, l’ICER négatif indique clairement que le projet B domine strictement le projet A.
Dans l’exemple des mesures d’économie d’eau (Tableau 3), si les projets deviennent mutuellement exclusifs (par exemple, la municipalité décide de ne réaliser qu’un seul projet), on constate immédiatement que le projet A domine fortement tous les autres projets. En effet, les ICER des autres projets par rapport au projet A sont négatifs. Par exemple, l’ICER de B par rapport à A est de -0,017 $/m3.
Dans le plan coûts-efficacité, un projet est fortement dominé par un autre lorsqu’il se situe dans le quadrant nord-ouest défini à partir d’un autre projet. À la Figure 4, on constate en effet que les projets B et C sont strictement dominés par le projet A.
Exercice: Cinq mesures pour sauver des vies
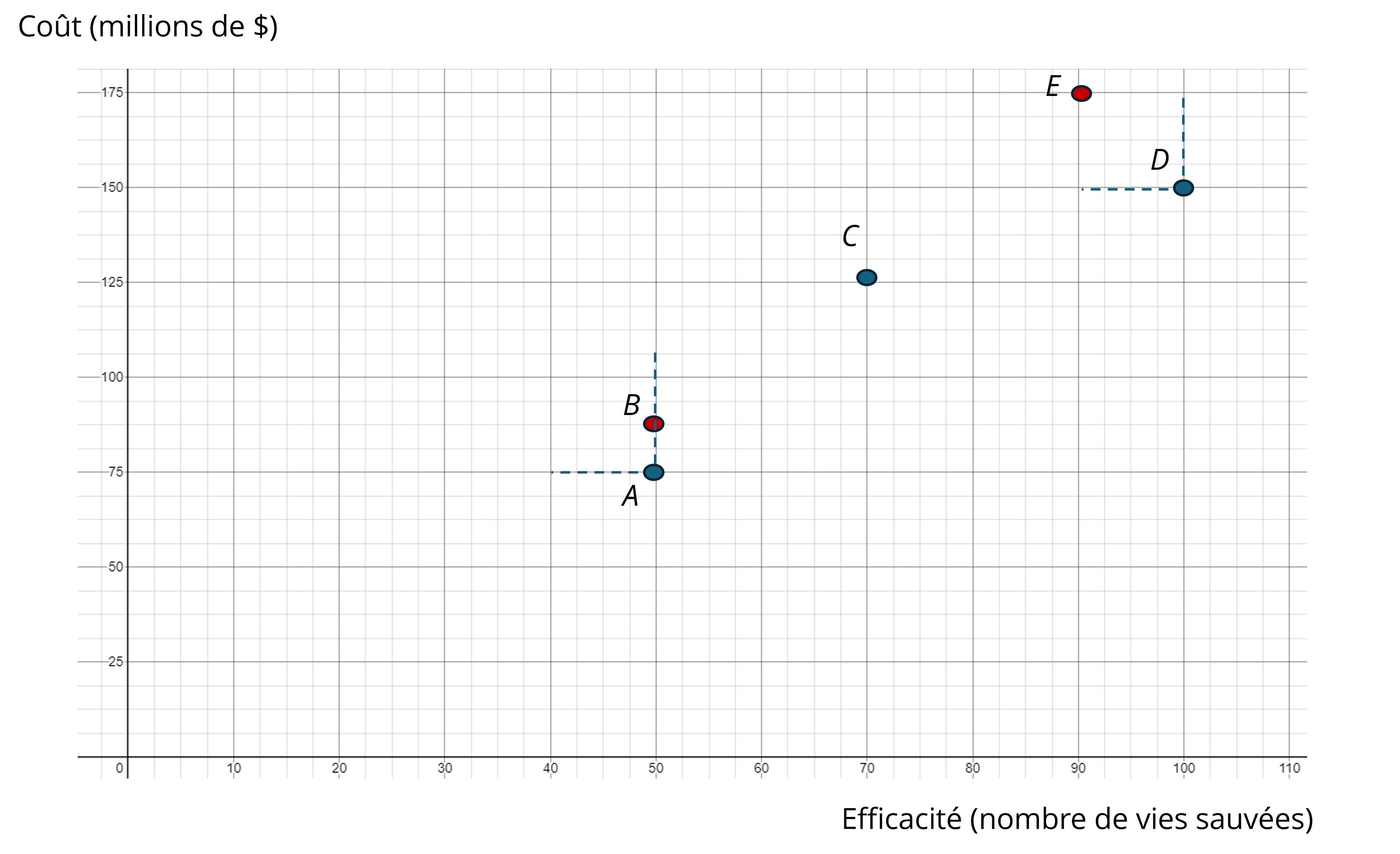
Le Tableau 4 montre le coût et l’efficacité de cinq mesures pour sauver des vies qui sont mutuellement exclusives. Représentez ces cinq projets dans le plan coûts-efficacité et déterminez si certains de ces projets sont strictement dominés.
| Mesure | Coût (millions) | Efficacité (vies sauvées) |
| A | 75 | 50 |
| B | 100 | 50 |
| C | 125 | 70 |
| D | 150 | 100 |
| E | 175 | 90 |
Résolution
L’analyse du Tableau 4 montre immédiatement que :
- La mesure B est strictement dominée par la mesure A ;
- La mesure E est strictement dominée par la mesure D.
La Figure 5 confirme que B se situe dans le quadrant nord-ouest, défini à partir du projet A et E dans le quadrant nord-ouest de D.
Il est également possible d’éliminer certains projets, parce qu’ils sont faiblement dominés (ou dominés par extension).
La dominance faible (ou par extension)
Un projet B est faiblement dominé par les projets A et C si les deux conditions suivantes sont respectées :
- 1) [latex]C_A[/latex] < [latex]C_B[/latex] <[latex]C_C[/latex], les projets sont classés par ordre croissant du coût total ;
- 2) ICER (B par rapport à A) > ICER (C par rapport à B).
En d’autres termes, si passer de A à B coûte plus cher par unité d’efficacité que passer de B à C, alors B est dominé faiblement. Le projet B doit être écarté, car l’argent dépensé pour augmenter l’efficacité est mieux utilisé pour passer directement au projet C, qui coûte moins par unité d’efficacité additionnelle.
Dans la Figure 6, les projets A, B et C sont ordonnés par ordre croissant du coût, de sorte que la condition 1 est respectée. De plus, on suppose que le seuil maximal acceptable est de 5 millions de dollars par vie sauvée, de sorte que les projets A, B et C respectent ce seuil.
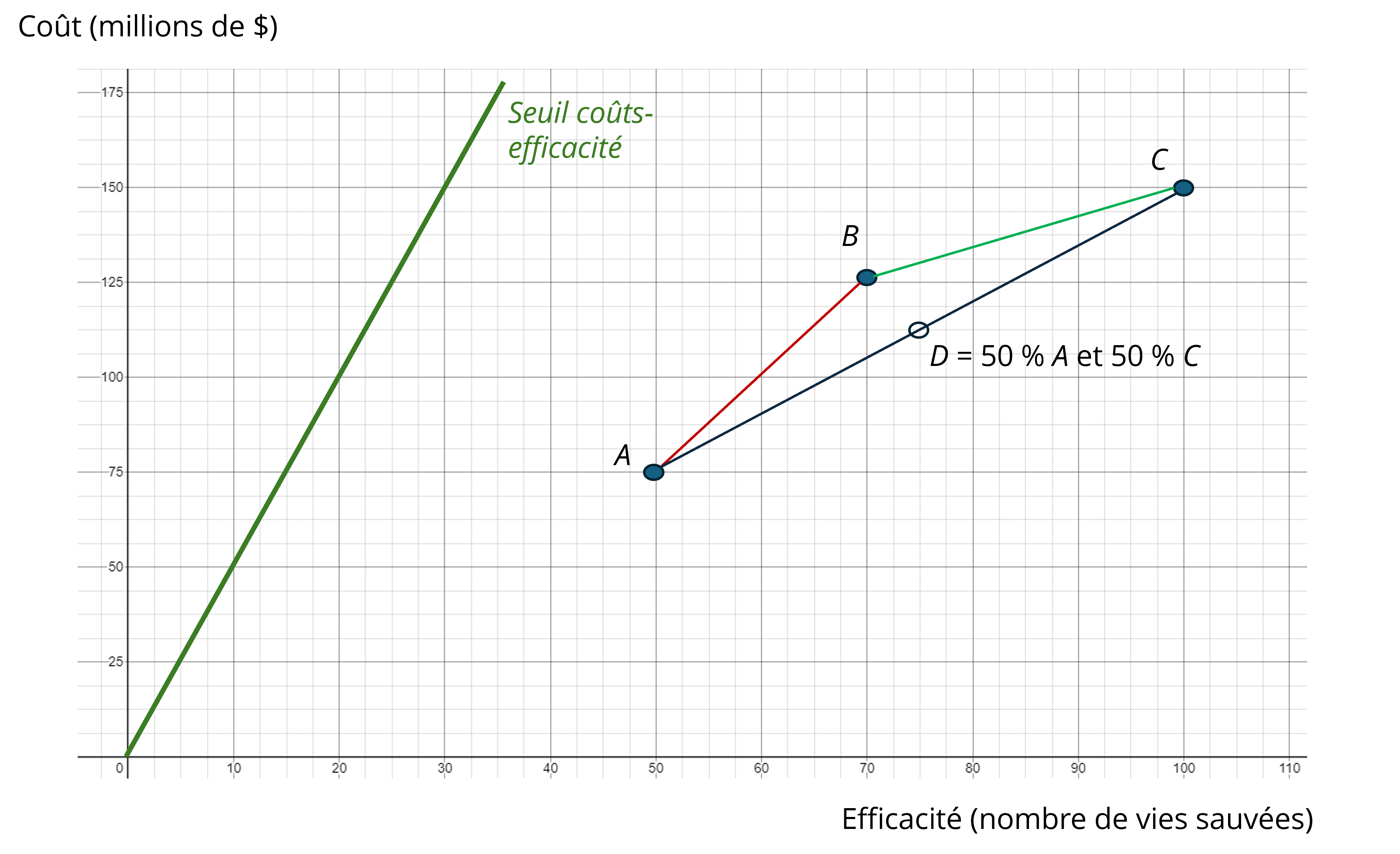
Graphiquement, l’ICER d’un projet par rapport à un autre projet correspond à la pente de la droite qui relie ces deux projets. Par exemple :
- L’ICER de B par rapport à A correspond à la pente de la droite en rouge qui unit A et B, soit (125 – 75) / (70 – 50) = 2,5 millions de dollars.
- L’ICER de C par rapport à B est égale à 0,83 millions de dollars, soit la pente de la droite en vert entre B et C.
On constate donc que le projet B est faiblement dominé par les projets A et C puisque la condition 2 est respectée (2,5 > 0,83).
Pourquoi un projet faiblement dominé doit-il être rejeté ?
Si l’ICER de B par rapport à A est inférieur au seuil retenu par les pouvoirs publics, alors automatiquement l’ICER de C par rapport à A le sera aussi, de sorte que les pouvoirs publics préféreront C à B. En effet, l’ICER de C par rapport à A correspond à la pente de la droite qui relie A à C (ligne bleue dans la Figure 6), et celle-ci est, par construction, inférieure à la pente de la droite rouge AB.
Une autre manière de comprendre pourquoi le projet B ne sera jamais choisi est la suivante : il serait possible de concevoir un nouveau projet D qui combine, selon certaines proportions, les projets A et C, et qui domine strictement le projet B. Le projet D constitue donc une combinaison linéaire des projets A et C, de sorte qu’il se situe sur la droite AC bleue.
Par exemple, le projet D pourrait consister à réaliser le projet A et C, mais sur seulement 50 % de la population initialement visée par ces projets. En supposant que les coûts et l’efficacité s’ajustent de manière proportionnelle, le projet D coûterait 112,5 millions de dollars (soit ½ 75 + ½ 150), avec une efficacité de 75 vies sauvées (½ 50 + ½ 100). Ce projet sauve plus de vies et coûte moins cher que le projet B.[6]
À partir de ces concepts, il est suggéré de procéder à l’analyse séquentielle suivante lorsqu’on compare trois options ou plus mutuellement exclusives.
L’analyse séquentielle d’options mutuellement exclusives
- 1) Classer les options par ordre croissant du coût total ;
- 2) Éliminer les options dont le ratio coûts-efficacité moyen dépasse le seuil critique ;
- 3) Supprimer les options qui sont strictement dominées ;
- 4) Calculer les ICER séquentiels, c’est-à-dire les ICER qui comparent chaque option par rapport à la précédente ou l’absence de projet pour l’option la moins coûteuse ;
- 5) Supprimer les options qui sont faiblement dominées ;
- 6) Recalculer les ICER séquentiels à partir des options restantes ;
- 7) Éliminer les options dont le ICER séquentiel excède le seuil critique.
L’option recommandée est celle dont le ICER séquentiel est le plus élevé parmi les options qui n’ont pas été éliminées.
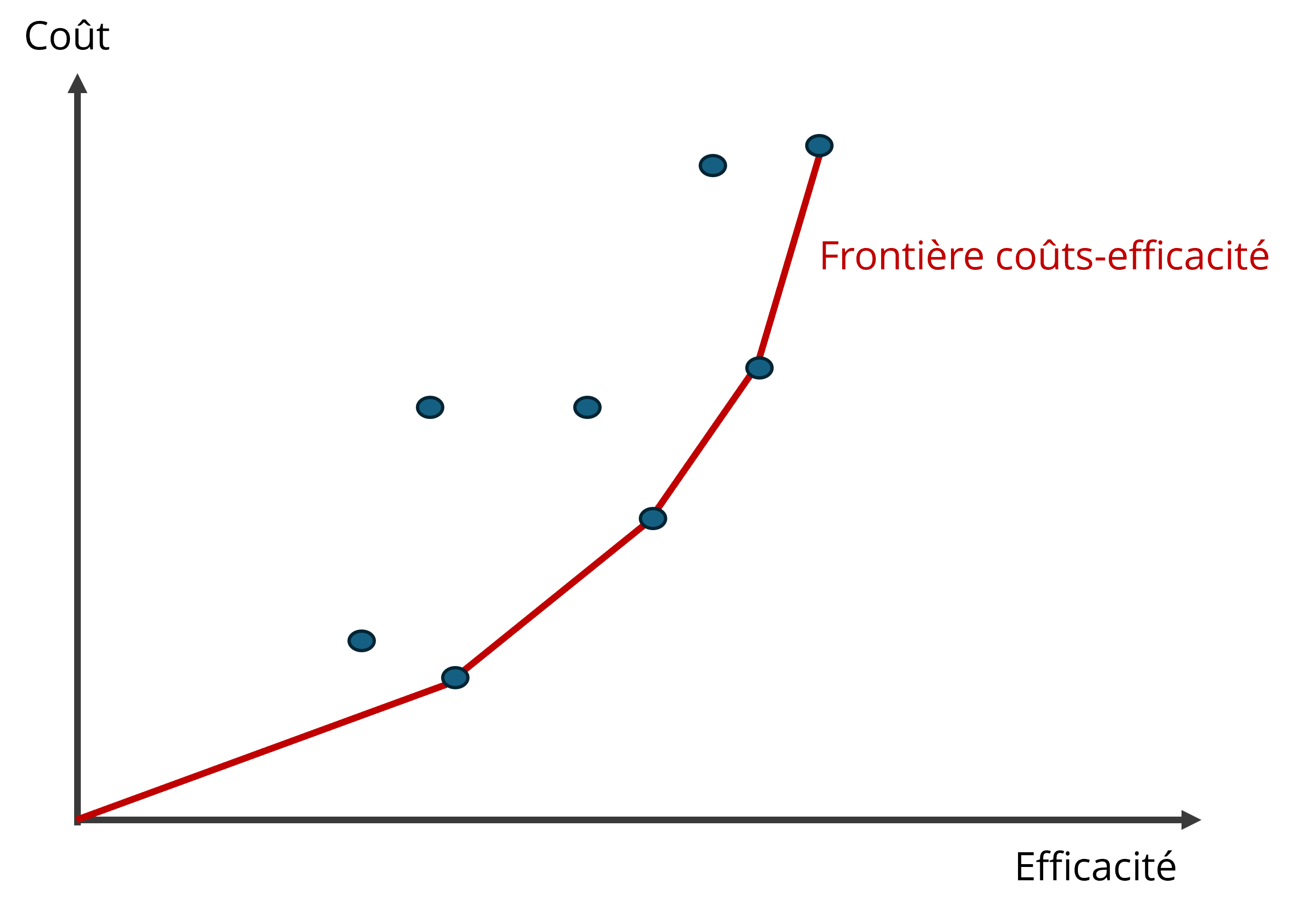
Graphiquement, la procédure séquentielle revient à déterminer la frontière coûts-efficacité dans le plan coûts-efficacité. Cette frontière correspond à l’enveloppe convexe établie à partir du sud-est du nuage de points constitué par les différentes options qui passent sous le seuil critique, comme l’illustre la Figue 7.
Exercice : L’ACE de 6 vaccins
Le Tableau 5 présente le coût et l’efficacité de 6 vaccins pour prévenir une maladie aux conséquences graves chez certains groupes de la population. Les autorités publiques ont fixé un seuil maximal de 2 000 $ par cas évité. Un seul vaccin peut être utilisé par patient. Effectuez une ACE de ces vaccins.
| Vaccin | Coût par dose ($) | Efficacité (%) |
| A | 400 | 30 % |
| B | 700 | 45 % |
| C | 750 | 40 % |
| D | 980 | 65 % |
| E | 1250 | 70 % |
| F | 1430 | 72 % |
Résolution
Toutes les options se situent dans le quadrant I, car elles améliorent l’efficacité à un certain coût. Le Tableau 6 montre le ratio coûts-efficacité moyen, soit l’ICER par rapport à l’absence de vaccin et l’ICER séquentiel.
| Vaccin | Ratio coûts-efficacité moyen ($) | Coûts différentiel* ($) | Efficacité différentielle* (%) | ICER séquentiel ($) |
| A | 1 333 | 400 | 30 | 1 333 |
| B | 1 555 | 300 | 15 | 2 000 |
| C | 1 875 | 150 | -5 | – 3 000 |
| D | 1 507 | 230 | 15 | 1 533 |
| E | 1 785 | 270 | 5 | 5 400 |
| F | 1 986 | 180 | 2 | 9 000 |
* Par rapport au scénario précédant pour les vaccins B à F et par rapport à aucun vaccin pour le vaccin A
On note d’abord que tous les vaccins ont un ratio coûts-efficacité inférieur au seuil critique de 2 000 $. Ensuite, le vaccin C est strictement dominé par le vaccin B. Son ICER séquentiel est négatif, car bien qu’il soit plus coûteux, il offre une efficacité inférieure. Par conséquent, cette option doit être écartée de l’analyse. Le Tableau 7 montre les ICER séquentiels après l’élimination du vaccin C, de sorte que D est maintenant comparé à B.
| Vaccin | Coûts différentiels ($) | Efficacité différentielle (%) | ICER séquentiel ($) |
| A | 400 | 30 | 1 333 |
| B | 300 | 15 | 2 000 |
| D | 280 | 19 | 1473 |
| E | 270 | 5 | 5 400 |
| F | 180 | 2 | 9 000 |
À partir de ce nouveau tableau, on constate que le vaccin B est faiblement dominé par les vaccins A et D, puisque l’ICER séquentiel de B est supérieur à celui de D. Il faut donc éliminer ce vaccin et recalculer l’ICER de D par rapport à A (voir le Tableau 8).
| Vaccin | Coûts différentiels ($) | Efficacité différentielle (%) | ICER séquentiel ($) |
| A | 400 | 30 | 1 333 |
| D | 580 | 35 | 1657 |
| E | 270 | 5 | 5 400 |
| F | 180 | 2 | 9 000 |
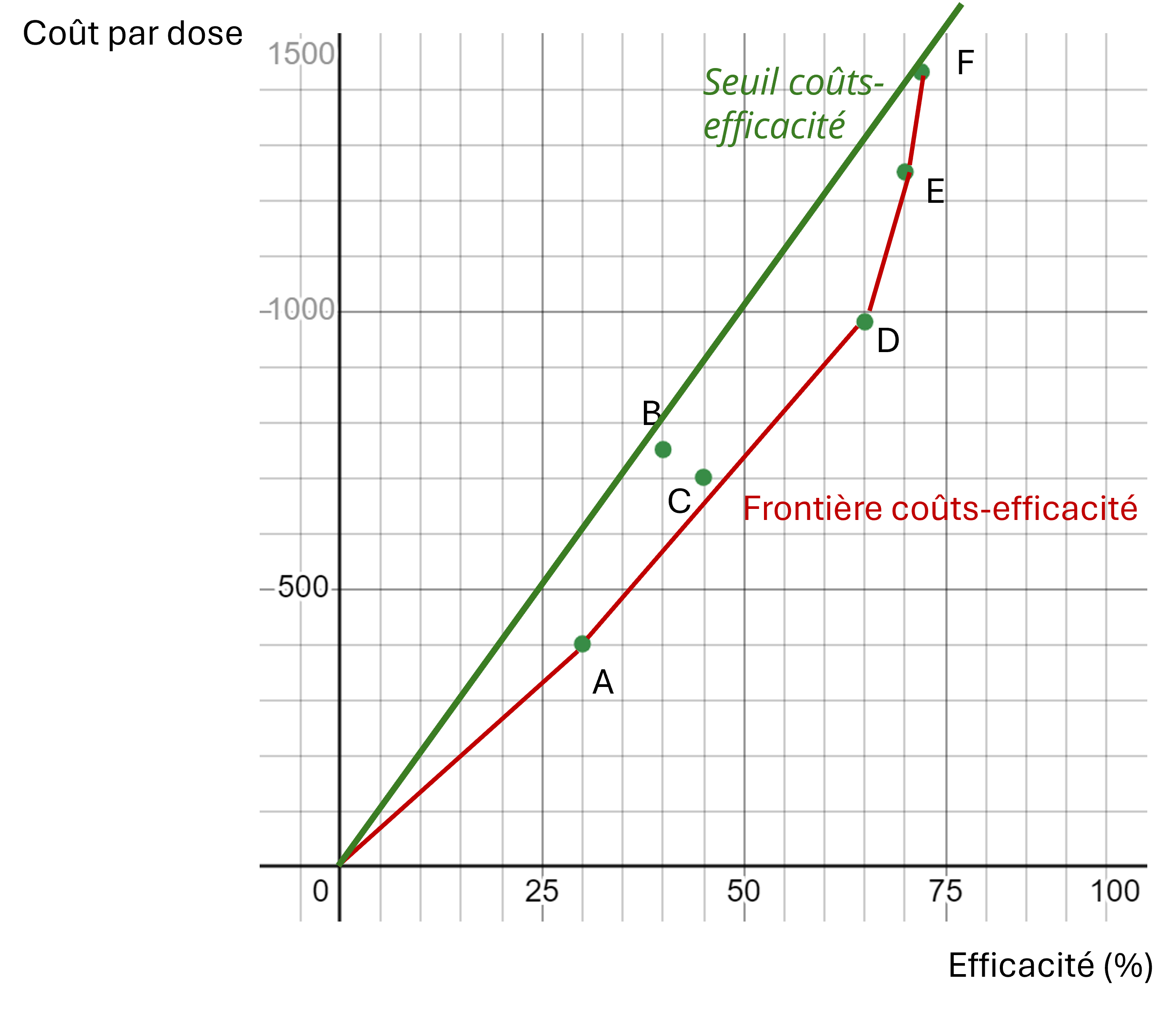
On constate que l’ICER séquentiel des vaccins A et D passe sous le seuil critique de 2 000 $. La Figure 8 illustre cette analyse dans le plan coûts-efficacité. Tous les points se situent sous le seuil critique, et la frontière d’efficacité est définie par les vaccins A, D, E et F, de sorte que les vaccins B et C ne seront jamais sélectionnés. On remarque enfin que la pente des segments entre DE et EF de la frontière est supérieure à la pente de la droite du seuil critique, ce qui signifie que l’ICER séquentiel de E et F excède le seuil critique.
La recommandation doit donc porter sur le vaccin D, puisqu’il offre l’efficacité la plus importante parmi les vaccins dont le ratio coûts-efficacité moyen et l’ICER séquentiel respectent le seuil.
20.3 L’analyse coûts-utilité
20.3.1 Les principes de base
L’analyse coûts-utilité (ACU) est semblable à l’analyse coûts-efficacité, mais elle se distingue par l’utilisation d’un indicateur d’efficacité synthétique visant à évaluer l’impact sur le bien-être (ou l’utilité) des bénéficiaires des projets comparés.
Cette méthode est principalement employée dans le domaine de la santé, avec plusieurs agences nationales d’évaluation des technologies de la santé, telles que le National Institute for Health and Care Excellence au Royaume-Uni, la Haute Autorité de Santé en France et l’Agence des médicaments du Canada, qui en recommandent l’utilisation.
La mesure de l’efficacité combine des dimensions quantitatives et qualitatives. La dimension quantitative est souvent exprimée en années de vie gagnées, tandis que la dimension qualitative évalue la qualité de la vie associée à l’état de santé[7].
L’indicateur d’efficacité le plus couramment utilisé est le nombre d’années de vie ajustées par la qualité, connu sous l’abréviation anglaise de « QALYs » pour « Quality-Adjusted Life-Years », largement utilisée même dans les documents en français. La section suivante décrit plus en détail la notion de QALY[8].
Pour le reste, la détermination des coûts, les ratios et les processus de sélection de projets sont identiques à ceux de l’ACE.
20.3.2 L’efficacité mesurée par les gains de QALYs
La notion de QALY prend en compte à la fois l’impact d’un projet sur la durée de vie et la qualité de la vie associée à l’état de santé. Cet indicateur synthétique prend la valeur 1 (QALY = 1) pour une année de vie en parfaite santé d’une personne et une valeur égale à 0 en cas de décès. L’indicateur prend une valeur inférieure à 1 lorsqu’une personne vit une année en ayant des problèmes de santé qui affectent sa qualité de vie. Par exemple, une année de vie en souffrant de douleurs chroniques invalidantes pourrait avoir une valeur de 0,5, de sorte que deux années de vie dans cette condition est équivalente[9] à une année de vie en bonne santé (2 x 0,5 = 1). Il est également possible que certains états de souffrance intense et incontrôlable correspondent à une valeur du QALY inférieure à 0, soit un état pire que la mort. Des indicateurs alternatifs au QALY ont été créés, comme le DALY pour « Disability-Adjusted Life Year » (année de vie ajustée en fonction de l’incapacité), qui est présenté brièvement à l’Annexe 1.
À partir de cet indicateur, il est possible de mesurer l’efficacité d’interventions, de traitements ou autres types de projets ayant un impact sur la durée et la qualité de la vie. Par exemple, l’efficacité d’un traitement pour prolonger la vie d’une personne atteinte d’un cancer terminal sera mesurée par le nombre total de QALY additionnels grâce à son traitement.
De manière plus formelle, l’efficacité d’un projet mesuré en termes différentiels de QALY (DQALY) prend la forme suivante :
[latex]\Delta QALY = \sum_{t=1}^{T} \frac{QALY_t}{(1+s)^t} = \sum_{t=1}^{T} \frac{1 \times u_t}{(1+s)^t}[/latex]
avec T le nombre d’années de vie supplémentaires que procure le projet par rapport à la situation de référence, et un score d’utilité ou de qualité de vie associé à l’état de santé[10] durant l’année [latex]t[/latex], avec [latex]u_t = 1[/latex] [latex]u_t = 0[/latex] et qui représentent respectivement une bonne santé et la mort ,et s le taux d’actualisation social.
Exercice : Comparaison de deux traitements contre les douleurs d’une maladie en phase terminale
Le traitement A contrôle la douleur, mais de manière limitée, ce qui procure un score d’utilité de [latex]u_B = 0,4[/latex] avec une durée de vie attendue de [latex]T_A = 9[/latex] . Le traitement B contrôle la douleur de manière plus efficace, menant à un score d’utilité de [latex]u_A=0,9[/latex], mais les effets secondaires mortels sont plus importants, de sorte que l’espérance de vie est de [latex]T_A = 5[/latex] ans. La valeur actualisée du coût du traitement A s’élève à 60 000 $, et celle du traitement B à 100 000 $. Le taux d’actualisation social est de 4 %. Déterminez les ratios coûts-utilité des deux traitements. Quel(s) traitement(s) recommandez-vous si le seuil critique est fixé à 20 000 $ par QALY, par l’organisme qui détermine la liste des médicaments qui sont remboursés ?
Résolution
Le Tableau 9 présente le coût, les gains de QALY et le ratio coûts-utilité des deux traitements par rapport à l’option de ne rien faire. Les gains de QALY annuels sont constants, de sorte qu’il suffit de les multiplier par le facteur d’annuité approprié. Par exemple, pour le traitement A, si l’on suppose des avantages tout au long de l’année, le facteur d’annuité avec T = 9 et s = 4 % est égal à 7,58, de sorte que le gain de QALY est de 3,03. On constate que le traitement B est plus efficace que le traitement A, mais qu’il coûte plus cher. Sur la base du seuil critique, il faut recommander le remboursement du traitement A, mais pas celui du traitement B, qui dépasse le consentement à payer.
| Traitement | Coût actualisé ($) | Gain de QALY actualisé | Ratio coûts-utilité |
| A | 60 000 | 0,4 x 7,58 = 3,03 | 19 802 |
| B | 100 000 | 0,9 x 4,54 = 4,08 | 24 473 |
Exemple : Trajectoires de qualité de la vie liées à la chimiothérapie
La chimiothérapie constitue un bon exemple pour illustrer la sensibilité des QALY aux trajectoires de qualité de vie complexes. Les patients sous chimiothérapie subissent généralement une baisse importante de leur qualité de vie durant le traitement, en raison des effets secondaires, mais leur qualité de vie et leur espérance de vie augmentent à plus long terme. La Figure 9 présente l’évolution du score d’utilité chez un patient atteint d’un cancer particulier, suivant qu’il entreprend ou non une chimiothérapie.
En calculant la différence entre les deux courbes et en actualisant, il est possible de déterminer le gain de QALY associé au traitement de chimiothérapie.
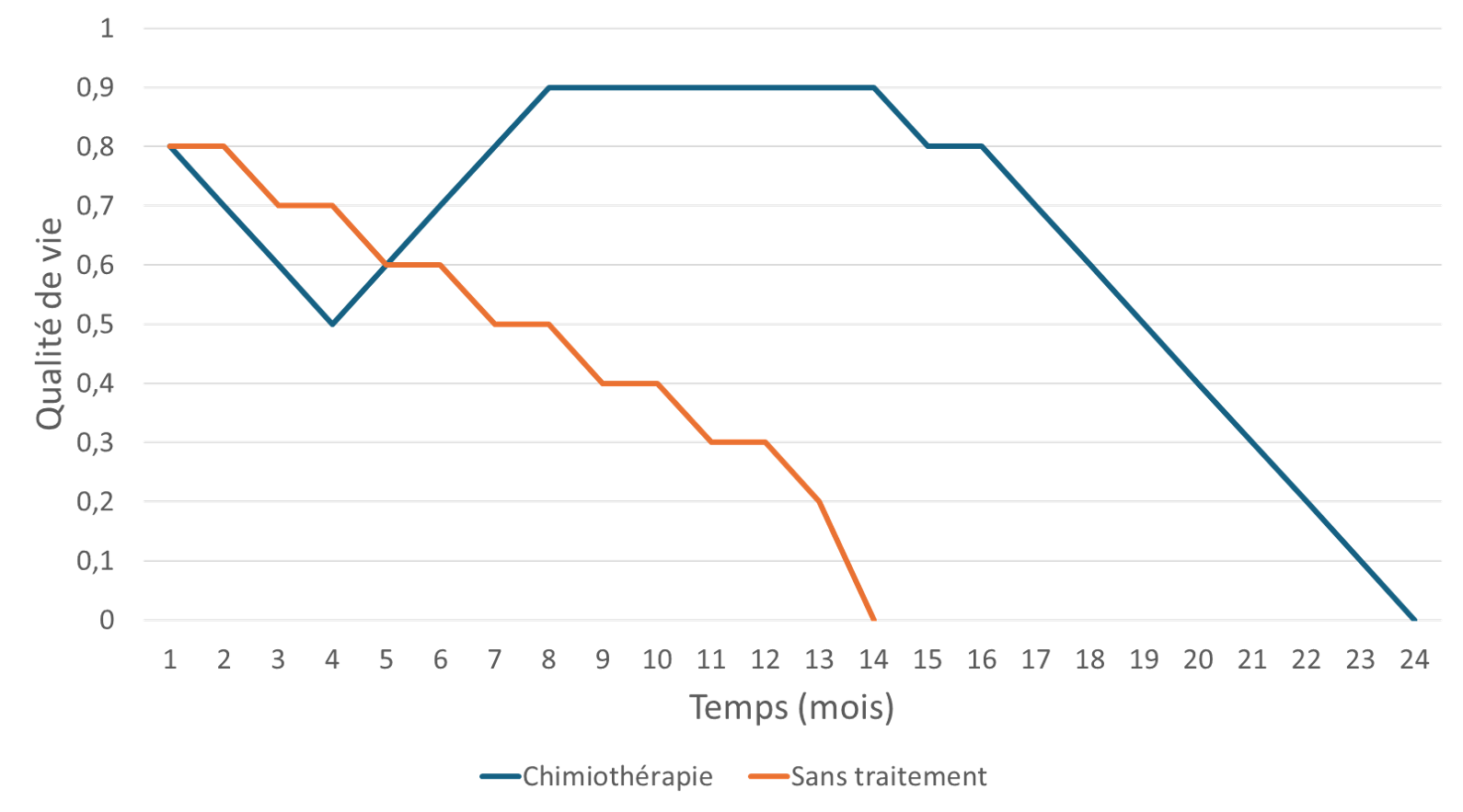
Figure 9. Qualité de vie avec ou sans traitement de chimiothérapie chez un patient atteint d’un cancer incurable
20.3.3 L’estimation du QALY
Étant donné qu’il s’agit d’un bien non marchand, l’évaluation du score d’utilité associé à un état de santé peut être évalué sur la base de certaines des techniques présentées dans la partie III. On peut distinguer les méthodes directes de celles fondées sur le transfert de valeur.
Les approches directes
Les méthodes directes ou de préférences déclarées utilisent des questionnaires, afin d’évaluer le score d’utilité de différents états de santé. Trois principales approches permettent de révéler ces scores d’utilité.
- L’échelle visuelle analogue (EVA)
Dans cette approche, les répondants classent divers états de santé sur une échelle de 0 à 100, allant du « plus préférable » au « moins préférable » (voir la Figure 10). L’enquête peut cibler la population générale, des experts médicaux ou des personnes affectées par les conditions évaluées. Chaque état de santé est décrit, et le répondant le place sur l’échelle. Cette méthode est rapide et simple, mais elle présente l’inconvénient de fournir une mesure ordinale plutôt que cardinale, puisque la distance entre les états de santé varie selon les répondants. De plus, l’absence de dimension temporelle ne permet de comparer que des états de même durée. Par exemple, il est impossible de comparer un mois avec une jambe dans le plâtre à cinq ans avec des maux de tête.

- L’arbitrage temporel (TTO pour “Time Trade-Off”)
Le TTO demande aux répondants de choisir entre des alternatives pour lesquelles il existe un arbitrage direct entre l’état de santé et la durée de vie. Par exemple, un individu doit choisir entre vivre T années dans un état de santé imparfait avec une utilité [latex]u_j[/latex]< 1, ou vivre X années dans un état de santé parfait avec une utilité [latex]u_i[/latex]= 1, où X ≤ T. Si l’individu exprime une préférence, un nouveau scénario lui est proposé avec une valeur différente de X, jusqu’à ce qu’il atteigne l’indifférence entre les deux options. À ce stade, on peut déduire le score d’utilité [latex]u_j = \frac{X*}{(T)}[/latex] . La Figure 11 illustre un exemple où une personne est indifférente entre le fait de vivre quatre années en parfaite santé ou dix années avec une insuffisance cardiaque invalidante, ce qui donne un score d’utilité de 0,4 pour l’état de santé dégradé.
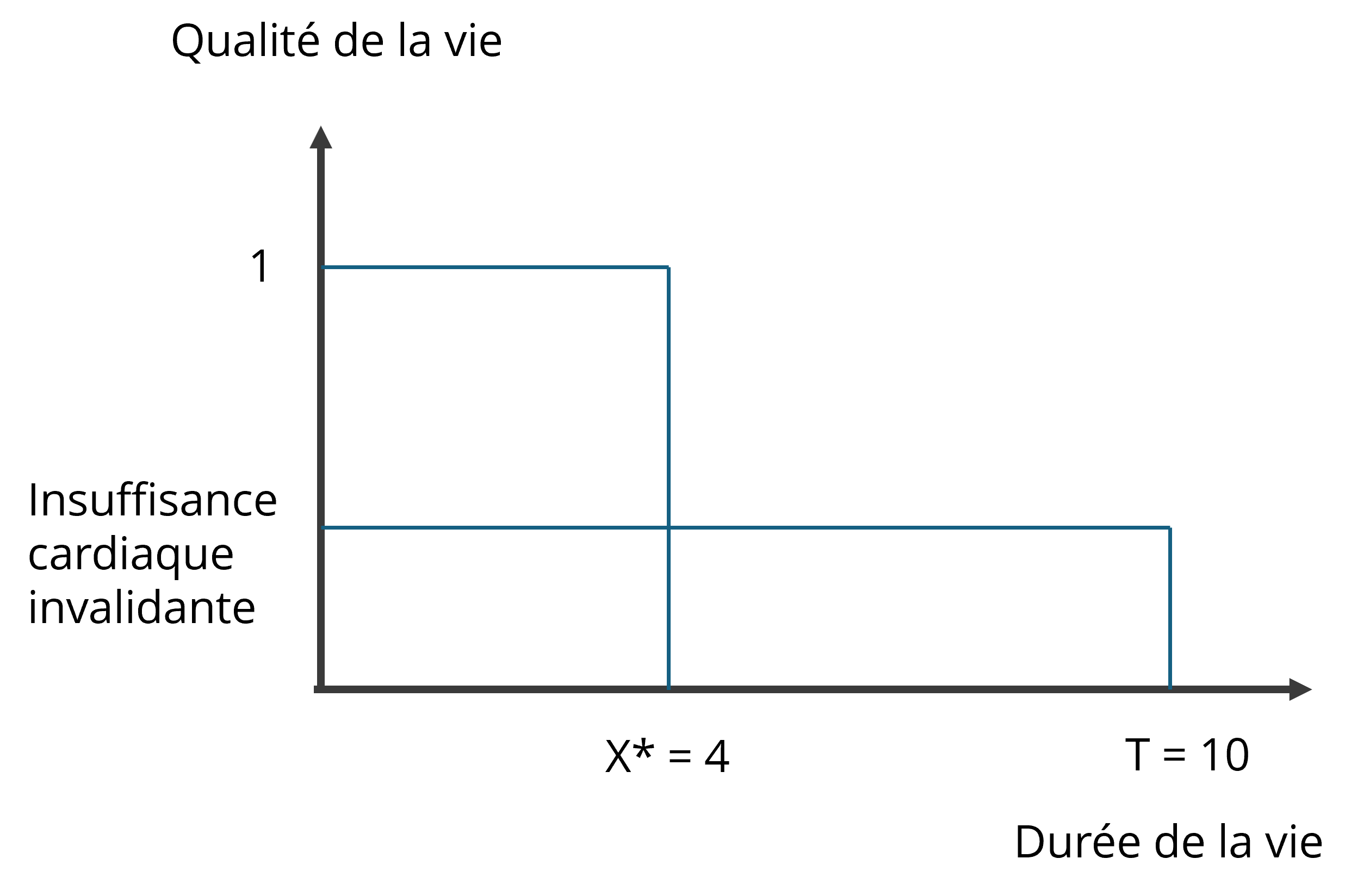
Bien que cette méthode soit relativement simple à administrer, elle devient problématique pour évaluer des états jugés pires que la mort, car le répondant devrait déclarer 0 année en parfaite santé plutôt que vivre avec un état dégradé.
Par ailleurs, il semblerait que l’utilité déterminée par TTO tende à diminuer avec la durée passée dans un état de santé (Brazier, Green, McCabe, et Stevens, 2003). Par exemple, un individu pourrait échanger 15 années de vie avec le diabète contre 12 années en bonne santé, ce qui donnerait une utilité de 0,8. Cependant, pour 30 années vécues avec le diabète, l’utilité pourrait baisser à 0,67, si l’individu préférait vivre 20 années en bonne santé. Ainsi, l’utilité reflète non seulement l’état de santé pendant une année, mais aussi un parcours de vie.
Enfin, la procédure ignore généralement les préférences temporelles des répondants, c’est-à-dire le taux d’actualisation qu’ils utilisent pour pondérer le présent et l’avenir (voir Johannesson, Pliskin et Weinstein, 1994). En effet, la procédure décrite pour déduire le score d’utilité suppose implicitement que les individus pondèrent de la même manière une année proche qu’une année dans l’avenir. Comme ce n’est pas le cas, cela signifie que les valeurs des scores d’utilité obtenus sont également affectées par les préférences temporelles des répondants. Cela engendre alors un risque de double actualisation, si ces valeurs sont utilisées pour calculer des gains de QALY en actualisant les gains futurs (voir MacKeigan, Gafni et O’Brien, 2002). Certaines procédures ont été proposées pour corriger cet enjeu, notamment en évaluant le taux d’actualisation des répondants (voir Lipman, Attema et Versteegh, 2020).
- Le pari standard (SG pour « Standard Gamble Method »)
Dans cette approche, le répondant doit choisir entre deux options (voir la Figure 12). La première consiste, par exemple, à subir une opération risquée, qui conduit à une loterie avec une probabilité p de recouvrer une santé parfaite (u = 1) pendant n années, et une probabilité (1 − p) de décéder (u = 0). La seconde option est la certitude de conserver un état de santé imparfait , comme des douleurs chroniques invalidantes au dos pour n années. Comme pour le TTO, plusieurs scénarios sont présentés, jusqu’à trouver le point d’indifférence permettant de déduire le score d’utilité [latex]u_j = p * 1 + (1-p) * 0 = p[/latex].
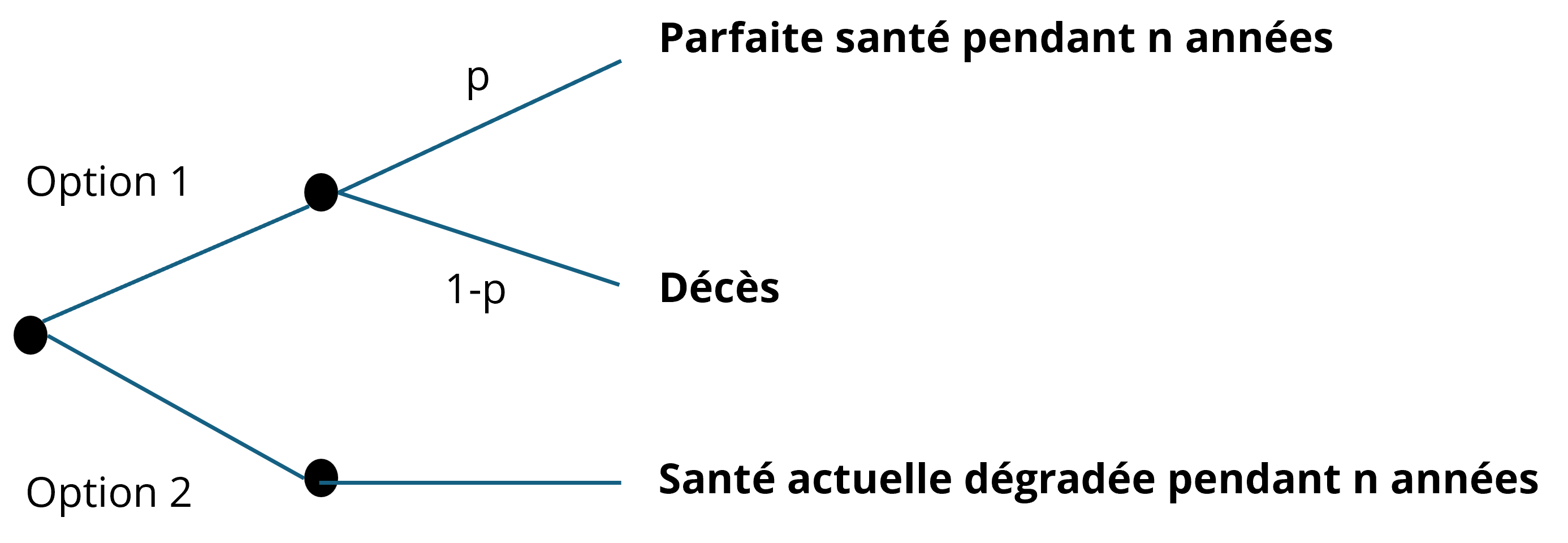
Cette approche présente l’avantage de s’appuyer sur la théorie de l’utilité espérée, mais elle comporte plusieurs limites. Les choix des répondants sont influencés par leur attitude face au risque, un paramètre qui devrait être pris en compte dans l’analyse. De plus, les choix proposés sont souvent inhabituels, et la compréhension des probabilités peut poser des difficultés à certains répondants. Enfin, à l’instar de la méthode TTO, cette approche présuppose que les répondants accordent le même poids au présent et à l’avenir (Gafni, 1994).
Les approches s’appuyant sur le transfert de valeur
Conformément aux principes décrits au chapitre 13, section 2, les approches fondées sur le transfert de valeur utilisent des scores d’utilité déjà établis dans d’autres études. Ces méthodes sont donc moins complexes et coûteuses à utiliser que les méthodes directes.
Des tables permettent désormais d’attribuer des scores d’utilité selon des conditions prédéfinies. Par exemple, une revue systématique a trouvé qu’une femme présentant des symptômes sévères de ménopause possède un score d’utilité de 0,58, calculé par TTO, contre 0,92 si elle suit une hormonothérapie de remplacement. Ces données sont disponibles pour divers types de maladies et de traitements. Dans le cadre d’une analyse coûts-utilité (ACU), la méthode du transfert consiste à utiliser les scores d’utilité issus de la documentation scientifique, avec des ajustements éventuels pour le contexte (inflation, conversion en monnaie locale et ajustement pour le niveau de vie).
Une variante consiste à utiliser un indice d’utilité multi attributs (MAUI, Multi-Attribute Utility Index). Cette méthode repose sur des questionnaires standardisés évaluant plusieurs aspects de la qualité de la vie, tels que la douleur, l’autonomie, la santé mentale et les capacités cognitives. Des études ont ensuite établi un lien entre les scores d’utilité mesurés directement par TTO ou par SG et divers paramètres décrivant les conditions de vie, facilitant ainsi le transfert de la valeur de la qualité de vie.
L’algorithme EQ-5D
L’EQ-5D est un système de classification de l’état de santé qui évalue cinq dimensions : la mobilité, l’autonomie, les activités quotidiennes, la douleur/inconfort et l’anxiété/dépression, à partir d’un questionnaire simple. Le répondant choisit pour chaque dimension qui correspond le mieux à son état. Par exemple, pour la dimension de la mobilité, le répondant peut sélectionner parmi les niveaux suivants :
– Niveau 1 : « Je n’ai aucun problème de mobilité. » ;
– Niveau 2 : « J’ai quelques problèmes de mobilité. » ;
– Niveau 3 : « J’ai beaucoup de problèmes de mobilité. » ;
– Niveau 4 : « Je ne peux pas me déplacer du tout. »
L’ensemble des réponses fournit un état de santé EQ-5D (3125 états sont possibles) auquel est associé un score d’utilité. Par exemple, une personne qui indique un niveau 1 pour chaque dimension aura un score d’utilité de 1. Pour plus d’informations, visionner la vidéo ci-dessous ou vous référer à Devlin, Parkin et Janssen (2020).
D’autres algorithmes existent pour évaluer l’état de santé et établir des scores d’utilité, tels que le SF-6D, utilisé dans divers contextes, le HUI, ou l’AQoL-8D. Certains questionnaires ont également été créés spécifiquement pour des populations particulières, comme les enfants (CHU9D).
La détermination des scores d’utilité est un domaine complexe et en évolution continue. Pour approfondir l’étude de ces méthodes, consultez les travaux de Brazier, Deverill, et Green (1999), Richardson, McKie, et Bariola (2014), et Fauteux et Poder (2017).
20.3.4 Les avantages et les limites de l’ACU
L’ACU partage les mêmes avantages et les mêmes limites que l’ACE. Par exemple, elle ne prend généralement pas en compte les bénéfices des projets qui ne sont pas liés à la santé des patients, tels que l’impact sur les proches. Cependant, par rapport à l’ACE, l’ACU présente l’avantage d’utiliser une mesure d’efficacité qui combine plusieurs dimensions.
L’ACU a été critiquée pour son absence de lien solide avec la théorie économique du bien-être, de sorte que le processus de sélection de projets selon cette méthode n’aboutit pas nécessairement à une amélioration de la richesse collective ou du bien-être. De plus, les mesures des scores d’utilité peuvent être subjectives et varier selon les individus, ce que l’ACU ne prend généralement pas en compte. Par exemple, la réduction de l’utilité due à la perte de mobilité pourrait être perçue comme plus importante pour une personne jeune que pour une personne âgée.
En outre, les mesures de QALY peuvent parfois mener à des formes de discrimination. Une intervention visant à prévenir la mort d’une personne jeune générera plus de gains en QALY que la même intervention chez une personne âgée, en raison de l’espérance de vie qui est différente[11]. De même, l’ACU pourrait discriminer les personnes handicapées dont le score d’utilité est plus faible.
Comme pour l’ACE, la sélection finale nécessite l’établissement d’un seuil critique. Au Royaume-Uni, le National Institute for Health and Care Excellence recommande un seuil compris entre 20 000 £ et 30 000 £ par QALY (de 35 000 $ à 53 000 $). L’Organisation mondiale de la santé préconise l’utilisation d’une valeur comprise entre une et trois fois le PIB par habitant. Il n’existe pas de seuil explicite au Canada, mais dans la recherche, des valeurs comprises entre 50 000 $ et 100 000 $ par QALY sont courantes.
Un autre enjeu avec l’ACU est sa faible sensibilité aux gains importants, mais de courte durée. Par exemple, une anesthésie pour une extraction dentaire, qui dure une heure et coûte 50 $, pourrait être jugée peu efficace pour le coût. En effet, en supposant que sans anesthésie, l’utilité est de 0, et qu’elle est de 1 avec l’anesthésie, l’ICER (Incremental Cost-Effectiveness Ratio) de l’anesthésie serait de 438 000 $/QALY, soit une valeur bien supérieure aux seuils mentionnés précédemment. Ainsi, une mesure évitant une douleur extrême à un coût absolu relativement raisonnable pourrait ne pas être considérée comme un coût efficace, en raison de la courte durée de son effet.
20.4 Conclusions
Éléments clés à retenir
- Complexité de l’ACA : Dans certaines circonstances, l’ACA peut s’avérer impossible ou trop complexe à utiliser. D’autres approches peuvent alors être utilisées comme alternatives.
- Analyse d’impacts économiques : Cette méthode permet de mesurer les effets d’un projet sur différents secteurs de l’économie en termes d’emplois, de valeur ajoutée ou de rentrées fiscales.
- Distinction des effets : L’analyse distingue les effets directs sur les premiers fournisseurs du projet, les effets indirects sur les fournisseurs secondaires et les effets induits ou multiplicateurs.
- Limitation des impacts économiques : Les impacts économiques ne mesurent pas les avantages d’un projet, de sorte que les résultats de ce type d’analyse ne doivent pas être utilisés pour justifier ou sélectionner un projet.
- Modèles d’analyse : Les analyses d’impacts sont souvent fondées sur des modèles qui supposent une économie de sous-emploi généralisé des ressources productives, ignorant ainsi les effets de déplacement de l’activité économique par le mécanisme des prix.
- Analyse coûts-efficacité : Cette méthode compare des projets en fonction de leur coût différentiel par unité d’efficacité additionnelle. L’efficacité est mesurée en unités physiques de l’avantage principal recherché.
- Application spécifique : L’analyse coûts-efficacité est particulièrement utile pour comparer des projets ayant un avantage principal semblable. La sélection de projets mutuellement exclusifs repose sur un processus séquentiel, comprenant l’élimination d’options fortement ou faiblement dominées.
- Analyse coûts-utilité: L’ACU est une forme particulière de l’analyse coûts-efficacité, principalement utilisée dans le domaine de la santé. L’efficacité y est mesurée par un indicateur d’utilité, souvent le QALY (Quality-Adjusted Life Year), qui combine l’espérance de vie et la qualité de la vie.
- Évaluation de la qualité de la vie : La qualité de la vie, en tant que bien non marchand, peut être évaluée par différentes approches de préférences déclarées ou au moyen d’un processus de transfert.
Retour sur la motivation
Dans les années 1970, les Forces armées des États-Unis ont identifié le besoin d’un avion-cargo capable de transporter de lourds équipements sur de longues distances, tout en étant en mesure d’atterrir dans des conditions difficiles. Au début des années 1980, la proposition de McDonnell Douglas (désormais Boeing) pour le développement de l’avion C-17 Globemaster a été retenue, avec un plan initial de livraison de 120 appareils. Cependant, le développement de cet avion a rencontré divers problèmes, notamment des dépassements de coûts, ce qui a conduit le Congrès américain, en 1993, à exiger une analyse indépendante pour déterminer si le programme C-17 devait être poursuivi ou si des alternatives s’avéreraient plus appropriées. Comment aborder cette évaluation ? Une analyse coûts-avantages ne convient pas ici, car la monétisation des avantages diffus poserait des défis considérables.
Résolution
Une analyse d’impacts économiques aurait permis de comparer les retombées économiques des différentes options considérées. Cependant, il est important de rappeler que ces retombées ne mesurent pas les avantages d’un projet et ne tiennent pas compte des coûts d’opportunité. Malgré ces limitations, ce type d’analyse est souvent utilisé pour promouvoir des programmes de défense (voir, par exemple, PwC Strategy &, 2024, sur les impacts économiques du programme de développement de l’avion de combat Eurofighter Typhoon).
Pour évaluer la pertinence de poursuivre le programme C-17, l’Institute for Defense Analyses a mené une analyse coûts-efficacité (ACE). Les étapes clés de cette analyse ont été les suivantes :
- Identification des alternatives au projet de référence : Les options envisagées comprenaient l’extension de la durée de vie des avions existants (C-141), la militarisation d’avions commerciaux comme le Boeing 747-400, le développement de nouveaux modèles et la réduction du nombre de C-17 commandés. Au total, 27 configurations de flottes, y compris le scénario de référence avec 120 C-17, ont été analysées. Toutes ces configurations avaient une capacité théorique de charge journalière semblable.
- Mesure de l’efficacité des 27 configurations : L’efficacité a été mesurée en termes de quantité de cargos (y compris du cargo surdimensionné) et de troupes pouvant être livrés dans un délai donné pour répondre à différents types de missions. Des modèles de simulation ont été utilisés, prenant en compte les caractéristiques et les contraintes de chaque configuration (temps de chargement, vitesse, autonomie de vol, besoin de ravitaillement en carburant, durée de vol maximale par jour, etc.).
- Évaluation des coûts : Les coûts ont été évalués en incluant le développement, l’acquisition, l’entretien et le soutien opérationnel pendant 25 ans, avec un taux d’actualisation de 4,5 %.
- Comparaison des alternatives dans un plan efficacité-coûts : Voir Greer, (2010).
Sur la base de cette ACE, il a été décidé de poursuivre le programme C-17 tel quel, car l’analyse a conclu qu’il était coût efficace par rapport aux autres options analysées.
Exercices
- À la suite d’un tremblement de terre, un gouvernement veut dépêcher une équipe de nettoyage. L’équipe de 32 personnes peut nettoyer 1 km2/h, au coût de 15 $ de l’heure par travailleur (projet A). Il est proposé d’augmenter à 48 personnes l’équipe de nettoyage, qui aurait alors une productivité de 1,8 km2 de l’heure, au même salaire horaire (projet B). Quel est le ICER (B par rapport à A) ?
- Une agence de santé effectue une analyse coûts-efficacité de quatre stratégies de traitement pour éviter les récidives d’AVC. Les coûts et l’efficacité dans le tableau ci-dessous sont calculés pour traiter annuellement toutes les personnes qui subissent un premier ACV. Toutes les valeurs ont été actualisées adéquatement. Quelle option recommandez-vous si une seule option doit être sélectionnée, et que le seuil critique s’élève à 15 000 $ par récidive évitée.
| Traitement | Coût ($) | Nombre de récidives évitées |
| A | 2 000 000 | 200 |
| B | 3 500 000 | 250 |
| C | 5 000 000 | 500 |
| D | 8 000 000 | 800 |
- Un organisme environnemental vous demande d’évaluer trois nouveaux projets de protection de milieux humides. Les coûts par superficie d’aires protégées sont listés en valeur actualisée dans le tableau ci-dessous. Le projet A est l’alternative en place (le statu quo), et les projets sont mutuellement exclusifs. Déterminez l’option qui doit être recommandée en fonction du seuil critique qui sera retenu par les pouvoirs publics.
| Projet | Coût ($) | Aire protégée (km2) |
| A (statu quo) | 410 000 | 60 |
| B | 830 000 | 65 |
| C | 890 000 | 79 |
| D | 900 000 | 75 |
- Vous êtes responsable d’évaluer si un programme de vaccination contre le zona chez les personnes de 50 ans et plus serait coût efficace. Vous savez que le zona peut laisser des séquelles neurologiques et être très douloureux s’il n’est pas traité rapidement, mais qu’il ne cause pas beaucoup de décès. Quel type d’analyse proposez-vous d’utiliser et pourquoi ?
- Des cardiologues s’intéressent à différents médicaments pour prévenir les maladies du cœur chez les patients à risques. Les nouveaux médicaments s’ajoutent à ceux que le patient prend déjà, car leurs actions sont complémentaires. Le Tableau 12 présente les coûts et la réduction annuelle du risque d’accidents cardiaques associés aux différentes thérapies. Les interventions sont classées selon un ordre établi par des considérations médicales.
| Ordre | Intervention | Coût | % de réduction du risque |
| 1 | A- Aspirine | 200 $ | 2,4 % |
| 2 | B – Aspirine + antihypertenseur | 600 $ | 4,1 % |
| 3 | C – Aspirine + 2 antihypertenseurs | 1500 $ | 7,3 % |
| 4 | Aspirine + 2 antihypertenseurs + hypocholestérolémiant | 6000 $ | 10,3 % |
Inspiré de Marshall (2003)
En supposant que les pouvoirs publics utilisent une norme maximale de 30 000 $ par accident cardiaque évité, déterminez l’intervention qui doit être sélectionnée.
6. Dans le cadre d’une consultation prébudgétaire, une coalition en faveur de la promotion de la culture au Québec a commandé une analyse des impacts économiques et fiscaux des dépenses culturelles (Paradis, Ruscio et Dufresne, 2020). D’après cette étude, il n’existe « aucune raison économique valable de ne pas investir en culture, même si le seul facteur considéré est le développement économique ». L’étude recommande ainsi une augmentation des dépenses culturelles par le gouvernement, en s’appuyant sur les arguments suivants :
- « La culture exerce un rayonnement important sur le reste de l’économie, à travers ses achats auprès de divers fournisseurs et les dépenses des travailleurs dans le reste de l’économie.
- Chaque dollar de production économique (PIB) en culture s’accompagne de 0,70 $ à 0,90 $ en production additionnelle dans le reste de l’économie (moyenne des industries : 0,70 $).
- Chaque tranche de 100 M $ dépensés en culture (excluant les télécommunications) représente 1540 emplois, soit nettement plus que la moyenne des industries québécoises (1030 emplois).
- Les revenus fiscaux des activités économiques associées à la culture compensent pour les subventions que reçoivent les organismes culturels. » (Paradis, Ruscio et Dufresne, 2020, p. 4).
Effectuez une analyse critique de ces arguments.
Annexe 1. La notion de DALY
Le DALY (Disability-Adjusted Life Year, ou Année de vie ajustée en fonction de l’incapacité) est une mesure qui évalue la charge de morbidité d’une population en combinant les années de vie perdues en raison de la mortalité prématurée (YLL, Years of Life Lost) et les années vécues avec une incapacité (YLD, Years Lived with Disability). Créé par la Banque mondiale dans les années 1990, cet indicateur est essentiel pour quantifier l’impact des maladies sur la santé publique.
Les composantes du DALY
- Les années de vie perdue : Cette composante mesure les années de vie perdues à cause des décès prématurés. Elle est calculée en soustrayant l’âge au moment du décès de l’espérance de vie moyenne. Par exemple, si une personne meurt à 50 ans, alors que l’espérance de vie est de 80 ans, cela correspond à 30 YLL.
- Les années vécues avec un handicap : Cette composante quantifie les années vécues avec une incapacité due à une maladie ou à une condition de santé. Elle prend en compte à la fois la prévalence de la condition et le degré d’incapacité, qui est exprimé par un poids variant de 0 (absence d’incapacité) à 1 (incapacité totale).
Le DALY est un outil clé dans l’évaluation des interventions de santé, notamment pour les analyses coûts-efficacité. En intégrant à la fois la mortalité et l’incapacité, le DALY permet de mesurer l’impact des interventions sur la santé de la population de manière globale. Les décideurs en santé publique peuvent comparer différentes interventions en termes de DALY évités. Par exemple, une campagne de vaccination pourrait réduire le nombre de DALY associés à une maladie infectieuse, tandis qu’un programme de prévention des maladies chroniques pourrait également montrer des résultats significatifs.
Bibliographie
Brazier, J., Deverill, M. et Green, C. (1999). A review of the use of health status measures in economic evaluation. Journal of Health Services Research & Policy, 4(3), 174–184. https://doi.org/10.1177/135581969900400310
Brazier, J., Green, C., McCabe, C. et Stevens, K. (2003). Use of visual analog scales in economic evaluation. Expert Review of Pharmacoeconomics & Outcomes Research, 3(3), 293-302. https://doi.org/10.1586/14737167.3.3.293
Centre de collaboration nationale des maladies infectieuses. (2015). Comprendre la mesure agrégée utilisée pour estimer la charge des maladies, Projet 211. https://ccnmi.ca/publications/comprendre-la-mesure-agregee-utilisee-pour-estimer-la-charge-des-maladies/
Devlin, N., Parkin, D. et Janssen, B. (2020). Methods for analysing and reporting EQ-5D data. Springer. https://www.ncbi.nlm.nih.gov/books/NBK565678/
Fauteux, V. et Poder, T. G. (2017). État des lieux sur les méthodes d’élicitation du QALY. International Journal of Health Preference Research, 1, 2-14. https://doi.org/10.21965/IJHPR.2017.001
Yeung, MW., Tuite, A., Ximenes, R., Cernat, A., Tunis, MC. et Sander, BH. (2024). Guide d’interprétation de l’économie de la santé. Gouvernement du Canada. https://www.canada.ca/fr/sante-publique/services/immunisation/comite-consultatif-national-immunisation-ccni/methodes-processus/guide-interpretation-economie-sante.html
Graig, D. H. (2007). Regional economic impact analysis and project evaluation. UBC Press.
Marchand, G. (2023). Le modèle intersectoriel du Québec : Fonctionnement et applications, Édition 2023. Institut de la Statistique du Québec. https://statistique.quebec.ca/fr/fichier/le-modele-intersectoriel-du-quebec-fonctionnement-et-applications-edition-2023.pdf
Marshall, T. (2003). Coronary heart disease prevention: insights from modeling incremental cost effectiveness. BMJ, 327(7426), 1264-1267. https://doi.org/10.1136/bmj.327.7426.1264
McEwan, P. J. (2012). Cost-effectiveness analysis of education and health interventions in developing countries. Journal of Development Effectiveness, 4(2), 189-213. https://doi.org/10.1080/19439342.2011.649044
Paradis, P. E., Ruscio, C. et Dufresne, É. (2020). Analyse des impacts économiques et fiscaux d’un développement durable et permanent de la culture du Québec. Coalition la culture, le cœur du Québec. https://raiq.ca/wp-content/uploads/2020/01/Me%CC%81moire-e%CC%81conomique-culture-CCCQ-AppEco_2020-VF.pdf
PwC Strategy&. (2024). Industrial and Economic Impact of the Eurofighter Programme, Final Study Report – Executive summary. https://eft-main-production-statamic.s3.amazonaws.com/pwc/pwc_executive-summary.pdf
Richardson, J., Mckie, J. et Bariola, E. (2014). Multiattribute utility instruments and their use. Dans A. J. Culyer (Éd.), Encyclopedia of Health Economics (vol. 2, p. 341-357). Elsevier. https://doi.org/10.1016/B978-0-12-375678-7.00505-8
Tuominen, P., Reda, F., Dawoud, W., Elboshy, B., Elshafei, G. et Negm, A. (2015). Economic appraisal of energy efficiency in buildings using cost-effectiveness assessment. Procedia Economics and Finance, 21, 422-430. https://doi.org/10.1016/S2212-5671(15)00195-1
Vahidnia, F. et Walsh, J. (2002). Cost-Effectiveness of Traffic Safety Interventions in the United States. Traffic Safety Center, Business, Housing and Transportation Agency, State of California. https://escholarship.org/uc/item/06w1b608
Yeh, S. S. (2010). The cost effectiveness of 22 approaches for raising student achievement. Journal of Education Finance, 36(1), 38-75. https://dx.doi.org/10.1353/jef.0.0029.
- Tel que mentionné au chapitre 12, cet argument ne s’applique pas aux projets financés par des parties externes à l’horizon spatial qui génèrent des impacts supplémentaires dans l’économie. Le deuxième argument reste cependant valable dans cette situation. ↵
- Pour une présentation plus détaillée, voir Graig (2007) et Institut de la Statistique du Québec (2023). ↵
- La distinction entre les effets directs et indirects dans les analyses d’impacts économiques est donc différente de celle employée dans l’ACA. ↵
- Pour simplifier, on suppose que, sans intervention, ces personnes à très haut risque vont développer la malaria à coup sûr. ↵
- Cette section s'inspire du Guide d'interprétation de l'économie de la santé, publié par le Gouvernement du Canada (2024). ↵
- Cette section s'inspire du Guide d'interprétation de l'économie de la santé, publié par le Gouvernement du Canada (2024). ↵
- En Anglais, Health-Related Quality of Life, abrévié HRQoL. ↵
- D’autres indicateurs comme le DALY (Disability-ajusted life-year) peuvent également être utilisés (voir le Centre de collaboration nationale des maladies infectieuses, 2015). ↵
- En supposant que le taux d’actualisation est égal à zéro. ↵
- Souvent les analyses dans le domaine médical simulent l’impact d’un traitement sur une population synthétique représentative. Dans ce contexte, chaque individu a une probabilité de décéder à la fin de chaque année, dépendant du traitement. Dans ce cas, le gain de QALY du traitement pour une personne prend la forme suivante : [latex]\Delta QALY = \sum_{t=1}^{T} QALY_t = \sum_{t=1}^{T} \Delta p_t \times \Delta u_t[/latex], avec T la durée maximale de l’analyse, c’est-à-dire le nombre d’années jusqu’à ce que toute la population disparaisse, [latex]\Delta p_t[/latex] le changement dans la probabilité de décès provoquée par le traitement et [latex]\Delta u_t[/latex] le changement dans le score d’utilité. ↵
- C’est la raison pour laquelle certaines législations aux États-Unis, comme The Patient Protection and Affordable Care Act (Obamacare), interdisent explicitement l’utilisation de cette approche. ↵

