18 L’incertitude, les risques et les biais
Motivation et objectifs d’apprentissage
 Pour faire face à la dégradation des matériaux d’un monument, les autorités ont le choix entre deux approches de restauration qui garantiront la même qualité de restauration. La première option utilise une approche traditionnelle pour laquelle l’estimation du coût d’un million de dollars est très fiable. La deuxième adopte une nouvelle approche encore peu employée, mais qui devrait permettre d’effectuer la restauration pour la moitié du coût. Elle comporte cependant la probabilité de 40 % de dépassement de coût de 350 %. Quelle option recommanderiez-vous ?
Pour faire face à la dégradation des matériaux d’un monument, les autorités ont le choix entre deux approches de restauration qui garantiront la même qualité de restauration. La première option utilise une approche traditionnelle pour laquelle l’estimation du coût d’un million de dollars est très fiable. La deuxième adopte une nouvelle approche encore peu employée, mais qui devrait permettre d’effectuer la restauration pour la moitié du coût. Elle comporte cependant la probabilité de 40 % de dépassement de coût de 350 %. Quelle option recommanderiez-vous ?
Dans le chapitre 6, nous avons présenté les règles de décision à appliquer dans le contexte de l’ACA. La règle de décision première veut qu’un projet soit recommandé si sa valeur actuelle nette (VAN) est positive, c’est-à-dire si ses avantages sociaux sont supérieurs aux coûts sociaux. Lorsque le choix porte sur deux projets mutuellement exclusifs, il faut sélectionner celui qui aboutit à la VAN la plus élevée. Ces règles supposent cependant que la VAN a été évaluée avec certitude, ce qui est rarement le cas dans la réalité. L’évaluation des coûts, des avantages et de la durée d’un projet s’avère le plus souvent incertaine et soumise à de nombreux risques. Comment documenter ces risques et ces incertitudes ? Comment affectent-ils la sélection de projets ? Y a-t-il des biais systémiques dans l’ACA ? Nous explorons ces enjeux dans ce chapitre.
À la fin du chapitre, vous serez en mesure de comprendre :
- Les notions de risque et d’incertitude et leurs implications pour la sélection de projets ;
- Les différentes formes d’analyses de sensibilité ;
-
Les causes de la malédiction des mégaprojets.
18.1 Incertitude, risques et choix de projets
Le risque correspond à une situation dans laquelle la réalisation finale est inconnue, mais les résultats possibles et leur distribution de probabilités sont connus a priori. En revanche, l’incertitude correspond à une situation dans laquelle la réalisation finale, les résultats possibles et leur distribution de probabilités sont inconnus a priori.
Par exemple, au jeu de pile ou face, les résultats possibles et leurs probabilités de réalisation sont connus a priori, ce qui en fait une situation à risque. En revanche, un projet de tunnel dans un sol qui n’a pas été caractérisé représente une situation incertaine, puisque l’ensemble des possibles et leurs probabilités de réalisation ne sont pas connus. Il est plus facile conceptuellement d’analyser les risques que l’incertitude.
On distingue le risque spécifique et le risque systémique. Le risque spécifique, aussi appelé « idiosyncratique » ou « diversifiable », résulte de facteurs aléatoires propres au projet. Par exemple, la VAN d’une campagne de vaccination va dépendre du taux de vaccination de la population, qui peut être impacté par des effets indésirables médiatisés. Le risque systémique, ou non diversifiable d’un projet résulte de facteurs généraux non spécifiques au projet, comme l’état de la conjoncture économique. La VAN d’une nouvelle autoroute sera moins élevée que prévue si la croissance économique est plus faible qu’attendue.
La VAN d’un projet dépend donc des risques spécifiques et systémiques, et elle est soumise à l’incertitude. Comment cela devrait-il affecter les règles de sélection ?
Les risques et les choix de projets
La théorie de l’utilité espérée de von Neumann et Morgenstern permet d’analyser la prise de décision dans un environnement risqué. Appliquée à l’ACA, cette théorie postule que le choix entre deux projets risqués dépend non seulement de la VAN espérée des projets, mais également de l’importance des risques et de l’attitude du décideur face à ces risques.
Illustrons ces notions à partir d’un exemple. Le Tableau 18.1 montre la VAN de deux projets mutuellement exclusifs. Le projet A comporte un risque, car avec une probabilité de 0,2, sa VAN est négative à -1 million de dollars, et avec une probabilité de 0,8, sa VAN est de 6,5 millions de dollars. La valeur espérée de la VAN de ce projet correspond à la valeur moyenne de sa VAN pondérée par les probabilités, soit :
Valeur espérée de la VAN du projet A = 0,2 x (-1 million $) + 0,8 x 6,5 millions $ = 5 millions $
Le projet B ne présente pas de risque, et sa VAN est également de 5 millions de dollars.
| Projet | VAN faible
(probabilités) |
VAN élevée
(probabilités) |
VAN espérée |
| A | -1 million $
(0,2) |
6,5 millions $
(0,8) |
5 millions $ |
| B | — | 5 millions $
(1) |
5 millions $ |
Dans ce contexte, la VAN espérée est la même, alors qu’un projet est risqué, tandis que l’autre ne l’est pas. Dans ce cas, la décision dépendra de l’attitude face aux risques du décideur. Si celui‑ci est neutre face aux risques, les deux projets seront jugés équivalents, puisqu’ils mènent à la même VAN attendue. En revanche, en cas d’aversion aux risques, le projet B sera préféré, puisque le projet B offre une valeur certaine. Le projet A sera préféré en cas de goût pour le risque, puisqu’il offre la possibilité d’obtenir plus de 5 millions de dollars.
Généralement, l’ACA s’effectue en supposant la neutralité face aux risques, de sorte que les règles de sélection en présence de risques deviennent :
- Projets non mutuellement exclusifs et sans contrainte budgétaire : Recommander les projets pour lesquels la valeur espérée de la VAN est positive ;
- Projets mutuellement exclusifs : Recommander le projet pour lequel la valeur espérée de la VAN est la plus élevée ;
- Projets en présence d’une contrainte budgétaire : Recommander le projet ou les projets qui mènent à la somme des valeurs espérées de la VAN la plus élevée et dont la somme des valeurs attendues des coûts respecte le budget.
L’hypothèse de neutralité face aux risques dans l’ACA est généralement justifiée par deux principaux arguments :
- La possibilité d’éliminer le risque spécifique d’un projet par la diversification de l’ensemble des projets menés. En effet, en présence d’un grand nombre de projets, on s’attend à ce que certains se comportent mieux que prévu, ce qui compensera pour les projets qui réussiront moins bien ;
- Le risque systématique d’un projet est faible.
La validité de ces justifications est néanmoins remise en question (voir Atkinson et al., 2018). En effet, la diversification complète n’est pas nécessairement possible, et les risques systémiques peuvent s’avérer non négligeables. De plus, l’importance de la demande d’assurance individuelle souligne la présence d’aversion face aux risques. Les choix collectifs devraient donc éventuellement refléter cette aversion. De plus, il est certainement avisé de ne pas sous-estimer les risques mineurs, mais qui pourraient entraîner des conséquences catastrophiques et irréversibles, une situation qui peut se produire lorsque l’on se focalise exclusivement sur la valeur attendue.
En pratique, il n’existe pas de manière uniforme et reconnue pour prendre en compte l’attitude face aux risques dans le processus de choix des projets. Le plus souvent, les risques sont analysés selon des analyses de sensibilité quantitative ou qualitative (voir section 18.2). Les résultats de ces analyses sont ensuite pris en compte de manière ad hoc pour établir des recommandations.
Des processus plus formels sont parfois employés par certaines autorités. Par exemple, les autorités françaises tiennent compte du risque systémique dans la détermination du taux d’actualisation social (voir chapitre 17). Il est également possible d’exiger que les coûts comprennent une réserve, afin de réduire la probabilité d’un dépassement de coût. Dans la mesure où le montant de cette réserve dépend de l’importance des risques et de l’incertitude, elle pourrait affecter la sélection des projets (voir la section 18.3).
L’incertitude et le choix de projet
L’incertitude, par nature, peut difficilement donner lieu à une analyse de sensibilité quantitative, puisque l’ensemble des résultats possibles et leurs probabilités de réalisation ne sont pas connus. L’incertitude fait donc le plus souvent l’objet d’une évaluation de type qualitative.
Dans un environnement caractérisé par l’incertitude, la flexibilité de pouvoir accélérer, reporter, modifier l’ampleur du projet, ou même décider de l’abandonner, devient particulièrement important. En d’autres termes, la souplesse d’un projet procure un avantage distinct, souvent désigné sous le terme de « valeur de quasi-option »[1]. Cette flexibilité permet de s’adapter aux changements et aux informations nouvellement disponibles, optimisant ainsi les résultats potentiels du projet en fonction de l’évolution du contexte.
Par exemple, lors de la décision entre l’implantation d’un système d’autobus rapide et celle d’un tramway, la première alternative se distingue par sa plus grande flexibilité, attribuable à des coûts initiaux moins élevés. Cette flexibilité s’avère particulièrement avantageuse face à des variations de la demande de transport en commun, rendant l’ajustement des itinéraires d’autobus plus simple et plus rapide par rapport à ceux d’un tramway. Cette caractéristique de flexibilité devrait être prise en compte dans l’ACA de ces deux options.
Il est possible d’évaluer l’avantage de ces différentes formes de flexibilité à partir des techniques d’analyse financière des options réelles, mais les applications dans l’ACA restent assez limitées (par exemple Kind et al., 2017 pour une application dans le domaine du contrôle des inondations).
18.2 L’analyse de sensibilité
La manière la plus courante de documenter les risques et l’incertitude dans l’ACA consiste à effectuer des analyses de sensibilité quantitative et qualitative.
18.2.1 L’analyse quantitative
L’analyse de sensibilité quantitative vise à documenter comment la VAN d’un projet évolue en fonction des valeurs des principaux paramètres de l’ACA. Comme nous l’avons mentionné au Chapitre 2, trois types d’analyse sont possibles :
- Par paramètre ;
- Par scénario ;
- Par simulation.
L’analyse par paramètre
L’approche la plus simple et la plus courante consiste à documenter comment la VAN change lorsqu’on modifie la valeur d’un paramètre à la fois. Par exemple, il peut s’agir d’illustrer comment la VAN évolue si l’on change le taux d’actualisation social. Si le taux de base s’établit à 5 %, l’analyse de sensibilité par paramètre recalculera la VAN en utilisant une valeur plus faible et une valeur plus élevée, par exemple 3 % et 7 %, soit les deux valeurs recommandées par le gouvernement du Canada (voir le Chapitre 17, section 4). L’analyse doit se concentrer sur les paramètres qui peuvent avoir un impact notable sur la VAN et dont la valeur est incertaine. Les résultats de ces changements sont souvent présentés sous forme d’un diagramme de Tornado (voir le Chapitre 2 pour un exemple).
Il est également possible de montrer l’évolution de la VAN en fonction d’un intervalle de valeur de paramètre. Par exemple, la Figure 18.1 expose l’évolution de la VAN d’un projet de développement d’une voie réservée pour une ligne d’autobus en fonction de l’achalandage annuel anticipé. Dans certains cas, cette approche permet de mettre en évidence le point mort ou le seuil de rentabilité du projet en fonction d’un paramètre, soit la valeur de ce dernier, telle que la VAN = 0. Dans notre exemple, il faut un peu plus de 30 000 utilisateurs par année pour rendre le projet socialement rentable. On suppose que la valeur des autres paramètres est fixée à leur valeur principale.
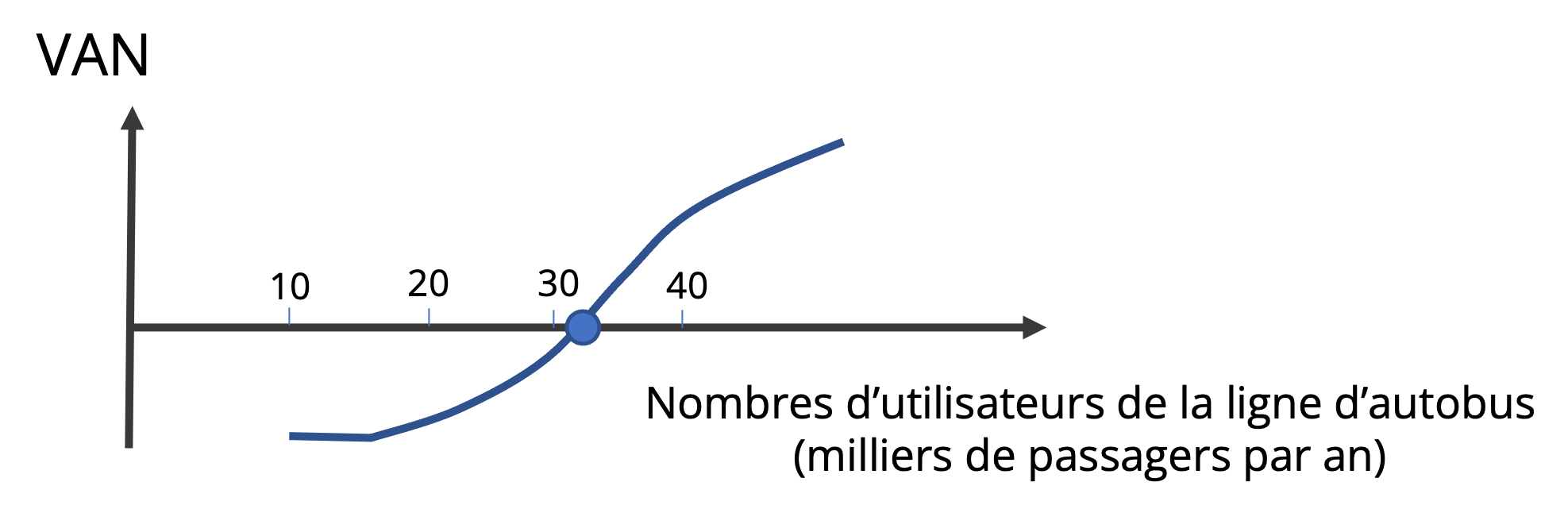
L’analyse de sensibilité par paramètre a l’avantage d’être simple et facile à interpréter. Cependant, elle ne fournit pas toujours une évaluation précise des risques entourant un projet, notamment si les valeurs de plusieurs paramètres sont corrélées. Par exemple, dans le cas de la ligne d’autobus, le nombre d’utilisateurs dépend de la croissance économique de la région, qui influence également la valeur du temps. Si le dynamisme économique dans la région est moindre que prévu dans le scénario principal, non seulement l’achalandage sera plus faible, mais la valeur des gains de temps par utilisateur du projet sera également moindre. C’est ce type de situation que permet d’analyser l’approche par scénario.
L’analyse par scénario
Dans cette approche, l’analyste construit différents scénarios correspondant à des combinaisons des valeurs des paramètres. À côté du scénario principal, il peut concevoir un scénario optimiste (par exemple, avec un coût moindre, un achalandage plus important, un taux d’actualisation plus faible, etc.) et un scénario pessimiste (dépassement de coût, croissance économique faible, valeur du temps réduite, etc.).
Comme l’approche par paramètre, l’approche par scénario est aussi relativement facile à mettre en application. Cependant, elle dépend des choix de l’analyste, ce qui ouvre la porte à la subjectivité. L’approche par simulation vise à systématiser et à expliciter les hypothèses sur les risques.
L’analyse par simulation
Avec cette approche, le risque lié à la valeur des paramètres clés est exprimé au moyen de fonctions de distribution statistique, telles que les distributions uniforme, triangulaire ou normale. Le choix de ces distributions devrait se fonder sur des observations historiques, des analyses empiriques ou des recommandations d’experts.
Une fois les propriétés statistiques des paramètres déterminées, on procède, par algorithme, à un très grand nombre de simulations, c’est-à-dire à des tirages de la valeur des paramètres (par exemple, un tirage aléatoire indique un taux d’actualisation de 5,45 % et une élasticité de la demande de 0,5). Chaque tirage de la valeur des paramètres permet de déterminer une valeur de la VAN. En effectuant un très grand nombre de tirages (par exemple, 10 000) qui mènent à une VAN différente, il est possible de simuler la distribution statistique de la VAN, comme l’illustre la Figure 18.2. Dans cet exemple, on trouve environ 40 % de chance que la VAN soit négative. Il est possible de calculer la valeur attendue et son écart-type (une mesure de dispersion[2]).
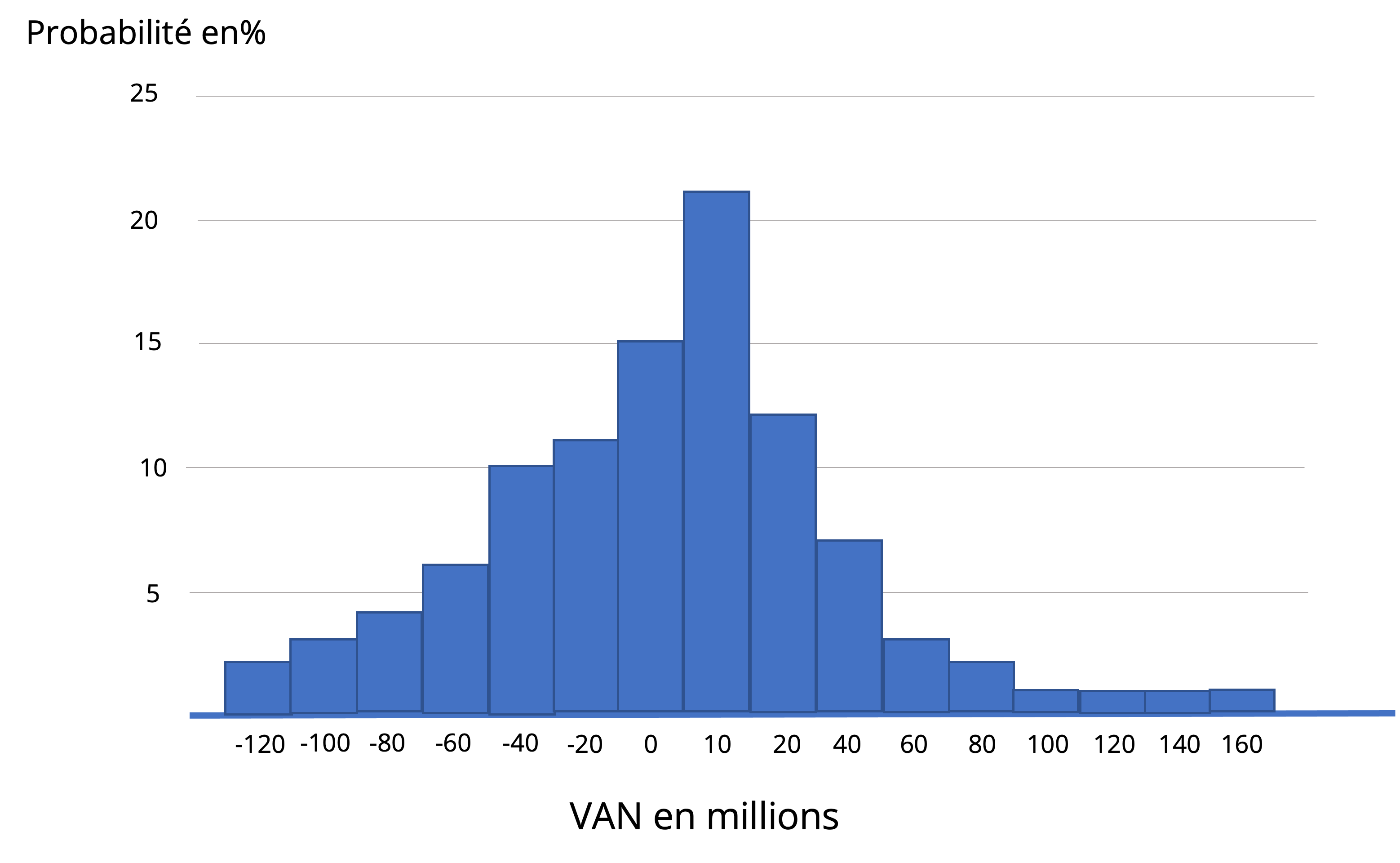
18.2.2 L’analyse qualitative
L’analyse qualitative vise à élargir la perspective, notamment en discutant de l’incertitude ou des risques qui ne peuvent pas être analysés dans l’analyse quantitative. Il peut s’agir de discuter des effets plus diffus que l’ACA ne prend pas en compte, mais que les décideurs pourraient vouloir considérer malgré tout. Certains des enjeux fréquents rencontrés par les projets sont discutés dans la prochaine section.
18.3 La malédiction des mégaprojets
Il n’existe pas de définition officielle d’un mégaprojet, mais d’après Flyvbjerg (2017), un mégaprojet présente généralement les caractéristiques suivantes : il est complexe, il dure plusieurs années, coûte généralement plus d’un milliard, implique de nombreux partenaires et entraîne des impacts importants.
Flyvbjerg et Bester (2021) ont analysé la performance de 2 062 projets publics provenant de 104 pays au cours de la période se situant entre 1927-2013, couvrant huit catégories d’investissements (ponts, bâtiments, systèmes de bus rapides, barrages, centrales électriques, trains et tunnels). La comparaison entre les prévisions et la réalisation montre une forte tendance à sous-estimer les coûts de 40 % en moyenne et à surestimer les avantages de 10 % en moyenne. Les avantages des projets de systèmes de bus rapides et des projets ferroviaires semblent particulièrement surestimés (environ 60 % et 35 % respectivement). De plus, ces grands projets sont généralement livrés avec beaucoup de retard par rapport à l’échéancier prévu.
Ces constatations ont amené Flyvbjerg (2017) à proposer une loi, « The Iron Law of Megaprojects », qui s’énonce comme suit : « Over budget, over time, under benefits, over and over again. ». En français, la malédiction des grands projets peut se résumer par la formule : « Dépassements de coûts, retards, avantages exagérés, encore et toujours »[3].
La malédiction des grands projets : le Réseau Express Métropolitain de Montréal.

Ce projet de métro léger, initié en 2015, prévoit à terme 67 km de rails et 26 stations. En 2016, le coût initial était évalué à 5,5 milliards de dollars avec une mise en service d’un premier tronçon en 2021. Après l’ajout de stations, le coût a augmenté à 6,3 milliards de dollars. En 2023, le coût prévu a bondi à 7,95 milliards de dollars, soit 45 % de plus que la première estimation, ce qui correspond au taux de dépassement moyen dans le secteur du rail. Le premier tronçon comprenant cinq stations a été mis en service à l’été 2023. Il est trop tôt pour se prononcer sur les avantages de ce projet.
L’étude de la performance des projets, réalisée par Marcellis-Warin et al. (2014) ainsi que Flyvbjerg (2011), identifie une série de facteurs de risque associés aux dépassements de coûts et de délais des projets, comme détaillé dans le Tableau 18.2.
| Facteurs de risques | Exemple |
| Caractéristiques du projet |
|
| Complexité du projet |
|
| Changements apportés en cours de réalisation |
|
| Processus de planification insuffisant |
|
| Gouvernance du projet |
|
| Instabilité politique et incertitude réglementaire |
|
| Facteurs externes |
|
| Facteurs économiques |
|
| Fraudes |
|
Cependant, il faut se poser la question de savoir pourquoi ces risques sont si souvent sous‑estimés lors des ACA. Selon Flyvberg et al. (2007) et Flyvbjerg (2011), le biais d’optimisme et la manipulation stratégique forment les causes profondes de la dérive récurrente des grands projets. Comme nous l’avons décrit au chapitre 3, le biais d’optimisme correspond à un biais cognitif conduisant à une sous-évaluation des risques. La manipulation stratégique désigne l’action intentionnelle de représenter un projet sous un jour favorable. Ce phénomène se manifeste particulièrement dans des environnements compétitifs où plusieurs projets rivalisent pour l’obtention de financements. Dans de tels contextes, les promoteurs, entrepreneurs, analystes et politiciens sont fortement incités à enjoliver la présentation de leurs projets. Flyvbjerg (2011) résume cette idée à travers l’équation suivante :
Sous-estimation des coûts + Surévaluation des avantages = Approbation du projet.
Pour contrer cette malédiction, Flyvbjerg propose d’ajuster les évaluations d’un projet en se fondant sur certaines expériences accumulées dans des projets semblables. La prévision par classe de référence (reference class forecasting) consiste donc à ajuster les prévisions internes d’un projet à partir de sources externes historiques. Cette procédure est utilisée au Royaume-Uni, aux Pays‑Bas, au Danemark ainsi qu’en Suisse.
Elle comprend trois étapes, que nous illustrons par une estimation des coûts :
- L’identification de la classe de référence, c’est-à-dire la désignation d’un ensemble de projets déjà réalisés et de nature comparable ;
- La distribution des probabilités dans la classe de référence du pourcentage des dépassement des coûts ;
- L’ajustement de l’estimation interne du coût du projet sur la base de la distribution externe et du risque de dépassement des coûts jugé acceptable.
Pour illustrer cette procédure, supposons un projet de train léger dont la distribution des probabilités du coût total a été estimée dans le cadre d’une ACA (voir Figure 18.3). L’espérance du coût du projet sur la base de l’évaluation interne monte à 800 millions de dollars. L’analyse de sensibilité montre cependant qu’avec ce montant, les probabilités de dépassement des coûts s’élèvent à 50 %. Par prudence, supposons que l’analyste ajoute une réserve de 26 millions de dollars, de sorte que le risque de dépassement des coûts soit réduit à 30 %.
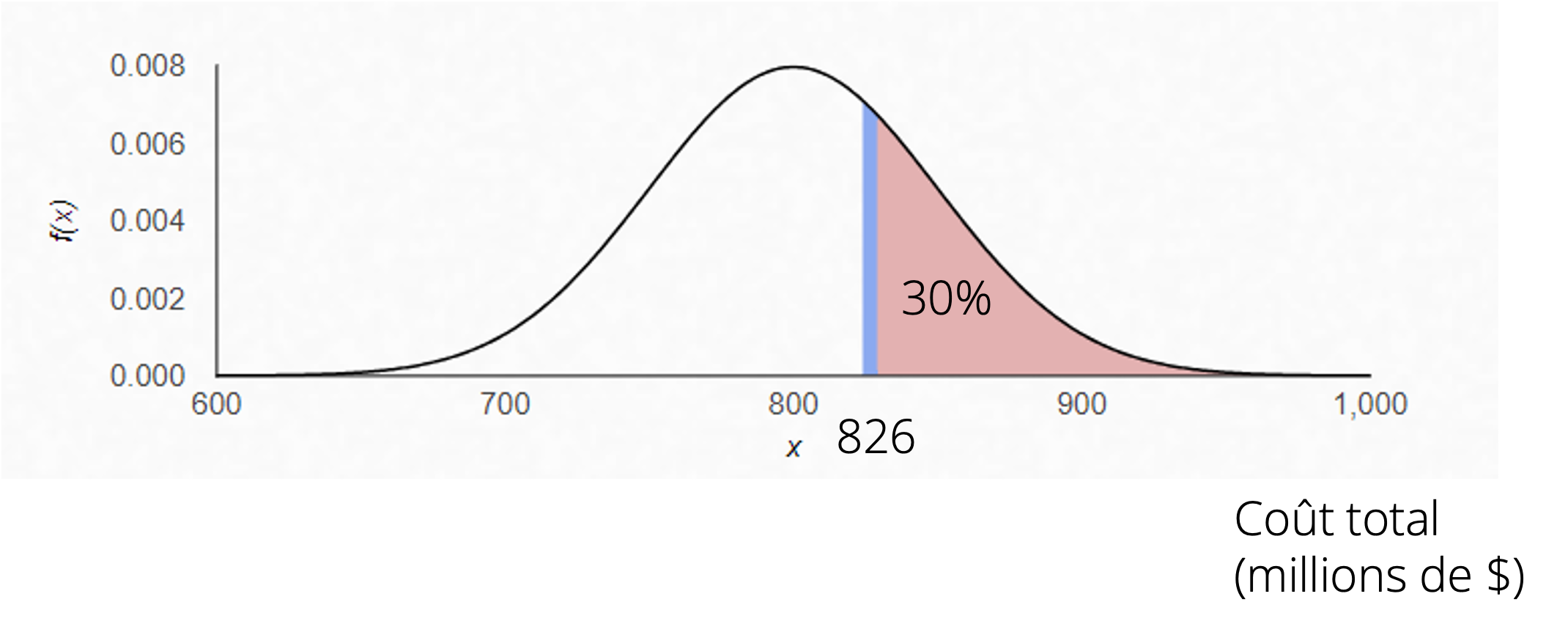
L’analyse externe des dépassements de coûts pour des projets comparables indique une distribution de probabilités telle qu’illustrée à la Figure 18.4. Le dépassement de coûts moyen pour ce type de projet est donc de 40 %. Cela signifie qu’il faudrait accroître la réserve à 40 % du montant initial du projet, de sorte que le coût du projet s’élèverait à 1,12 milliards de dollars. Avec cet ajustement, la probabilité de dépassement des coûts serait cependant de 50 %. Pour réduire ce risque à 30 %, l’ajustement du coût interne du projet devrait se situer à 50 %, de sorte que le coût total du projet soit de 1,23 milliards de dollars.
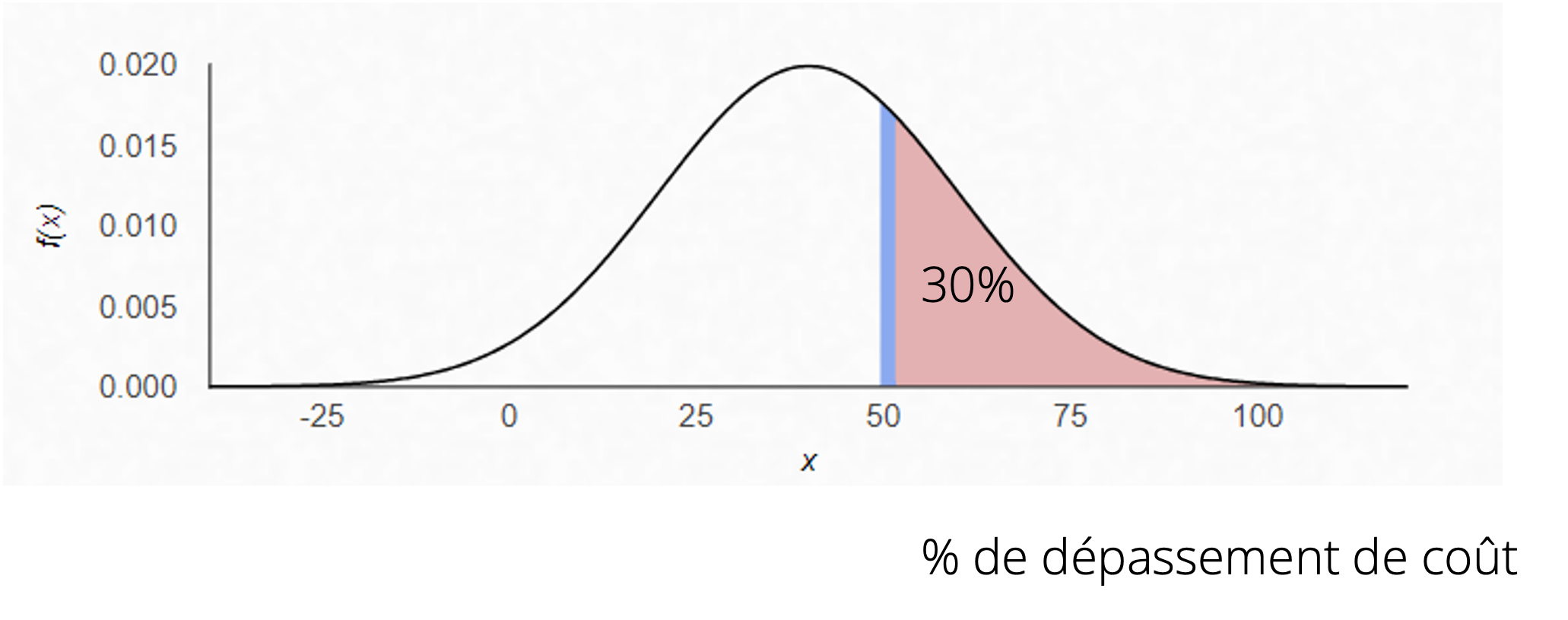
18.3 Conclusions
Éléments clés à retenir
- Les coûts, les avantages et l’échéancier d’un projet sont soumis à des risques et à des incertitudes qui doivent être documentés dans l’ACA au moyen d’analyses de sensibilité quantitative et qualitative.
- Les risques se caractérisent par un ensemble de réalisations possibles et une distribution de probabilités, tandis que l’incertitude correspond à des situations pour lesquelles les possibilités et leurs probabilités ne sont pas connues.
- On distingue les risques spécifiques du projet des risques systémiques provenant de l’environnement conjoncturel général.
- La manière de prendre en compte les risques et l’incertitude dans le processus de sélection de projets n’est pas uniforme dans la pratique.
- Les règles des décisions fondées sur la valeur espérée de la VAN impliquent la neutralité face aux risques, une hypothèse dont la validité est critiquée.
- La prise en compte du risque systémique s’effectue parfois par des ajustements du taux d’actualisation.
- La prise en compte des risques peut également se réaliser par l’inclusion de réserves, afin de réduire les risques de dépassement des coûts. Le montant des réserves devrait dépendre des risques et de l’incertitude du projet.
- L’analyse de sensibilité quantitative peut se réaliser par paramètre, par scénario ou par une analyse de Monte-Carlo.
- L’analyse du rendement des grands projets montre une tendance récurrente à une sous‑estimation importante des coûts, une surévaluation des avantages et des retards dans la livraison.
- Ces observations ne peuvent se comprendre par des erreurs aléatoires. Elles s’expliqueraient plutôt par le biais d’optimisme et par la manipulation stratégique des estimations.
-
La prévision par classe de référence est un moyen proposé pour améliorer l’évaluation des grands projets. Il s’agit d’effectuer des ajustements dans les estimations internes d’un projet en s’appuyant sur l’expérience acquise dans des projets comparables.
Retour sur la motivation
Pour faire face à la dégradation des matériaux d’un monument, les autorités ont le choix entre deux approches de restauration qui garantiront la même qualité de restauration. La première option utilise une approche traditionnelle pour laquelle l’estimation du coût d’un million de dollars est très fiable. La deuxième utilise une nouvelle approche encore peu employée, mais qui devrait permettre d’effectuer la restauration à la moitié du coût. Cependant, il existe une probabilité de 40 % de dépassement du coût de 350 %. Quelle option recommanderiez-vous ?
Réponse
Dans ce contexte décisionnel caractérisé par un risque défini, pour lequel les issues potentielles et leurs probabilités respectives sont clairement identifiées, l’adoption d’une posture de neutralité par rapport au risque du côté des autorités publiques conduit à privilégier une décision fondée sur le coût attendu des deux options de restauration.
L’approche traditionnelle : Cette méthode est associée à un risque quasi nul, avec un coût estimé à 1 million de dollars, offrant ainsi une prévisibilité financière totale.
La nouvelle approche : Le calcul de la valeur attendue du coût dans cette méthode se détaille comme suit : 0,6 x 0,5 million (sans dépassement) plus 0,4 x [0,5 x (1 + 3,5)] millions (en cas de dépassement), ce qui équivaut à 1,2 millions de dollars.
Dans ces conditions, l’approche traditionnelle apparaît comme la plus judicieuse, offrant une solution moins coûteuse. Cette recommandation demeure inchangée, même dans l’hypothèse où les autorités publiques manifesteraient une aversion au risque, étant donné que l’option traditionnelle élimine toute incertitude financière à un coût attendu moindre.
Exercices
- (*) Un projet d’usine de biométhanisation vise à convertir les déchets organiques de gaz naturel des résidents d’une ville. Quels sont, d’après vous, les principaux paramètres et les principales données qui devraient faire l’objet d’une analyse de sensibilité dans ce projet ?
- Pour illustrer d’une manière simple le principe de la méthode de Monte-Carlo, supposons que les coûts d’un projet puissent varier uniformément entre 5 et 15 millions de dollars, tandis que les avantages du projet fluctueraient uniformément de 1 à 32 millions de dollars. Les deux distributions sont supposées indépendantes.
En utilisant Excel, effectuez 100 tirages aléatoires des coûts et des avantages. Calculez ensuite la VAN qui résulte de chaque tirage. Puis, déterminez la moyenne et l’écart-type de la VAN en vous appuyant sur ces 100 simulations.
Déterminez ensuite, à partir des résultats de vos 100 tirages, les estimations du coût, de manière que la probabilité de dépassement de coût soit de 50 % et de 25 %.
AIDE : Fonctions EXCEL à utiliser TABLEAU.ALEA (ou alternativement RAND), MOYENNE, STDEV, PERCENTILE
Bibliographie
Atkinson, G., Groom, B., Hanley, N. et Mourato, S. (2018). Environmental Valuation and Benefit-Cost Analysis in U.K. Policy. Journal of Benefit-Cost Analysis, 9(1), 97–119. https://doi.org/10.1017/bca.2018.6
Boardman, A. E., Greenber, D. H., Vining, A. R. et Weiner, D. L. (2018). Cost-benefit analysis: Concepts and practice (5e éd.). Cambridge University Press.
De Marcellis-Warin, N., Peignier, I., Leenhouts, R., Teodoresco, S. et des Chênes, M. (2014). Étude des facteurs de risques de dépassements de coûts dans les projets de construction de routes et de grands travaux au Québec (2014RP-13), CIRANO. https://cirano.qc.ca/files/publications/2014RP-13.pdf
Flyvbjerg, B. (2011). Over budget, over time, over and over again: Managing major projects. Dans P. W. G. Morris, J. Pinto et J. Söderlund (Éds.), The Oxford handbook of project management (p. 321-344). Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199563142.003.0014
Flyvbjerg, B. (2017). Introduction: The iron law of megaproject management. Dans B. Flyvbjerg (Éd.), The Oxford handbook of megaproject management (p. 1-18). Oxford University Press. https://doi.org/10.1093/oxfordhb/9780198732242.013.1
Flyvbjerg, B. et Bester, D. W. (2021). The cost-benefit fallacy: why cost-benefit analysis is broken and how to fix it. Journal of Benefit-Cost Analysis, 12(3), 395-419. https://doi.org/10.1017/bca.2021.9
Flyvbjerg, B., Holm, M. S. et Buhl, S. (2007). Underestimating costs in public works projects: error or lie? Journal of the American Planning Association, 68(3), 279-295. https://doi.org/10.1080/01944360208976273
Kind, J., Wouter Botzen, W. J. et Aerts, J. C. (2017). Accounting for risk aversion, income distribution and social welfare in cost‐benefit analysis for flood risk management. WIREs Climate Change, 8(2), 1-20. https://doi.org/10.1002/wcc.446
Différence entre la somme des avantages et des coûts en dollars de l’année de référence, obtenue à l’aide d’une actualisation.
Étude de l’évolution de la valeur actualisée nette lors de changements des paramètres et des prévisions. Il existe trois types d’analyse de sensibilité : par paramètre, par scénario et par simulation de Monte-Carlo.
Rendement auquel la collectivité renonce en investissant dans un projet.
Outil d’évaluation économique d’un projet alternatif à l’ACA.
Elle consiste à calculer les entrées, les sorties et les besoins de financement pendant la durée du projet ; établir son montage financier, c’est-à-dire déterminer les modes de financement (emprunts, émissions d’obligations) et répartir les responsabilités entre les partenaires.
Il ne s’agit donc pas d’une évaluation des coûts et des avantages sociaux du projet, mais plutôt des coûts et des avantages financiers des partenaires. Cette analyse sert notamment à évaluer la rentabilité privée du projet pour ses partenaires. Les données produites dans le cadre d’une analyse financière sont souvent très utiles pour la réalisation d’une ACA.
Variation en pourcentage de la quantité demandée à la suite d’une variation de 1 % du prix. Elle s’exprime souvent en valeur absolue, donc sans le signe négatif. Une demande parfaitement inélastique possède une élasticité-prix nulle et est représentée par une droite verticale. Une demande parfaitement élastique possède une élasticité-prix infinie et elle correspond à une droite horizontale.
Hausse générale des prix au fil du temps.
Situation liée à un nombre limité d’offreurs (monopole/oligopole) ou de demandeurs (monopsone/oligopsone), entraînant une réduction de la quantité échangée et une perte sèche. En présence de pouvoir de marché, le prix ne reflète plus le coût marginal ni la valeur marginale.
Erreur systématique dans la perception et le traitement de l’information.

