16 Applications : La valeur du temps, de la vie et du carbone
Un gouvernement envisage d’augmenter la limite de vitesse de ses autoroutes de 100 km/h à 120 km/h. Les principaux impacts à évaluer dans une ACA de ce projet sont les suivants :
- Les gains de temps engendrés par l’augmentation de la vitesse ;
- Les impacts sur la sécurité routière, étant donné que ce projet pourrait augmenter les risques d’accidents et de mortalité sur les routes ;
- Les impacts sur l’environnement, notamment en ce qui concerne les changements climatiques.
Cette ACA nécessiterait donc d’établir des « prix de référence », notamment pour une heure de temps de déplacement économisé, pour une vie humaine et pour une tonne de carbone. Comment les méthodes présentées dans les chapitres précédents permettent-elles de déterminer ces valeurs ?
Ce chapitre vise à répondre à cette question. La valorisation du temps, d’une vie et d’une tonne de carbone sont des impacts intangibles qui se retrouvent fréquemment dans les ACA. Le chapitre offre également un aperçu des connaissances acquises et des défis non résolus dans l’évaluation de ces effets.
À la fin de ce chapitre, vous vous trouvez en mesure de comprendre les enjeux associés à l’évaluation :
- Du temps ;
- De la vie humaine ;
- Du carbone.
16.1 La valeur du temps
16.1.1 La définition du concept
Le temps constitue une ressource précieuse possiblement impactée par un projet. Par exemple, un projet visant à améliorer les transports en commun peut réduire le temps de déplacement des usagers, tandis qu’un investissement dans les services d’urgence peut réduire les temps d’attente. Pour évaluer ces avantages, il est nécessaire d’estimer la valeur du temps, plus précisément la valeur du temps économisé.
La valeur du temps (VT) désigne la valeur monétaire que les individus attachent à la réduction du temps qu’ils doivent consacrer à une activité spécifique. Elle est communément exprimée en termes monétaires par heure économisée.
La VT correspond donc au montant maximal que les individus sont prêts à payer pour économiser une heure qu’ils auraient autrement consacrée à une activité donnée. Cette valeur est déterminée par le coût d’opportunité, c’est‑à‑dire la valeur de cette heure dans son utilisation alternative la plus précieuse. L’utilisation alternative la plus évidente est le travail pour lequel une valeur monétaire est disponible, à savoir le salaire net. Cependant, un individu peut souhaiter consacrer l’heure économisée à une activité autre que le travail. Cela peut-il affecter sa VT ?
Becker (1965) propose un modèle théorique d’allocation optimale du temps dans lequel le temps est considéré à la fois comme un intrant pour la production de revenu (temps de travail) et pour la consommation (par exemple, il faut du temps pour cuisiner un repas, regarder un film ou pratiquer un sport). Dans ce modèle, l’allocation optimale du temps par l’individu aboutit à une VT à la marge qui est égale pour toutes ses activités, y compris pour le travail. Dans ce contexte, la VT est équivalente au salaire net, quel que soit l’usage de l’heure économisée. La VT est donc souvent évaluée par le salaire net.
Cependant, ce modèle suppose que les individus peuvent choisir librement leur nombre d’heures travaillées. En réalité, des contraintes existent sur le temps de travail, ce qui peut rendre la VT différente du salaire. Par exemple, si un individu est contraint de travailler plus d’heures qu’il ne le souhaite (par exemple, un employé à temps plein n’a pas la flexibilité de réduire ses heures de travail ou l’employeur le contraint à faire des heures supplémentaires), le salaire peut sous-estimer sa VT.
De plus, le temps alloué à une activité peut directement influencer l’utilité, ce qui rend la valeur du temps subjective et dépendante de l’activité et de l’individu. Par exemple, pour certaines personnes, le temps de déplacement lors d’un voyage peut être perçu comme un avantage plutôt que comme un inconvénient, car elles peuvent apprécier les paysages. Par ailleurs, le consentement à payer pour économiser une heure dans le trafic peut s’avérer plus élevé que celui pour réduire le temps de déplacement dans un environnement sans congestion. Une heure d’attente à un arrêt de bus peut avoir une VT différente d’une heure passée dans le bus. De même, la VT peut être relative et dépendre de la durée totale du déplacement. Économiser 15 minutes sur un trajet d’une heure peut ne pas avoir la même valeur que sur un trajet de 10 heures.
En résumé, le salaire net peut servir de première approximation de la VT. Cependant, il est essentiel de déterminer plus précisément la VT associée à une activité particulière lorsque les gains de temps constituent une composante importante d’une ACA. Cela s’avère d’autant plus crucial lorsque les préférences individuelles, les contraintes de temps ou la nature spécifique de l’activité peuvent influencer la valeur que les individus accordent à leur temps.
16.1.2 La détermination empirique de la valeur du temps
La plupart des études sur la valeur du temps ont été menées dans le domaine du transport. Comme nous l’avons expliqué au chapitre 7, les choix de transport dépendent du prix généralisé, qui englobe non seulement les dépenses monétaires, mais également les coûts implicites, en particulier celui du temps. Par conséquent, il est possible de déduire la VT en examinant les choix réels ou hypothétiques en matière de transport. Par exemple, la valeur du temps peut être évaluée en observant les choix réels des voyageurs entre différents modes de transport ayant des vitesses et des coûts variés, tels que la voiture ou l’avion, ou entre une route à péage plus rapide et une route congestionnée, mais gratuite.
Cependant, il est de plus en plus courant d’utiliser l’analyse conjointe (voir le Chapitre 15), qui consiste à présenter à un échantillon de la population des choix de transport hypothétiques impliquant un arbitrage entre le temps et l’argent. Cette approche offre l’avantage de permettre d’analyser le comportement des individus face à l’introduction de nouveaux modes de transport, tel un système de train léger.
La détermination de la VT à partir de choix réels ou hypothétiques nécessite cependant la création et l’estimation de modèles mathématiques spécifiques, ce qui dépasse le cadre de ce manuel. Néanmoins, l’annexe 1 de ce chapitre présente une brève introduction au modèle de l’utilité aléatoire additive, qui se trouve à la base de nombreuses analyses en transport. De plus, l’encadré ci-dessous illustre un exemple de détermination de la VT à partir d’une analyse conjointe.
Il est également possible d’établir la VT associée à une activité spécifique en utilisant la méthode de l’évaluation contingente. Par exemple, Van Den Berg, Gafni et Portrait (2017) ont évalué la VT des patients dans un contexte hospitalier à Amsterdam, aux Pays-Bas. Ils ont évalué le consentement à payer pour réduire le temps d’admission, le temps de traitement, le temps d’attente ainsi que le temps de déplacement.
La VT dans un contexte universitaire

Barla et al., (2015) évaluent la VT des membres de l’Université Laval qui utilisent principalement l’automobile individuelle pour se rendre sur le campus. Cette évaluation est menée à l’aide d’une enquête en ligne dans laquelle les participants doivent effectuer des choix hypothétiques de modes de transport entre l’automobile individuelle, le bus et les modes de déplacement non motorisés. Deux attributs sont employés pour définir différents scénarios : les temps de déplacement et certaines composantes des coûts monétaires. Afin de rendre les scénarios hypothétiques plus réalistes, les répondants se voient rappeler leur situation actuelle, et les scénarios sont calibrés en fonction de celle-ci. Par exemple, les participants peuvent être invités à indiquer quel mode de transport ils choisiraient si les coûts de stationnement étaient doublés ou si le temps de déplacement en bus était réduit de 50 %. Un exemple de ce type de scénario est présenté dans le Tableau 16.1.
| Ci-dessous, votre situation actuelle (approximative) qui vous fait choisir l’automobile comme mode principal de déplacement. |
||
| Automobile | Bus | Mode non motorisé |
| Coût du stationnement | Abonnement | Coût |
| 300 $ par session | 200 $ par session | les mêmes que vous payez actuellement. |
| Temps de déplacement | Temps de déplacement | Temps de déplacement |
| 35 min. | 70 min. | les mêmes que vous payez actuellement. |
Quel mode de transport choisiriez-vous si vous étiez confronté aux conditions suivantes ? |
||
| Automobile | Bus | Mode non motorisé |
| Coût du stationnement | Abonnement | Coût |
| 600 $ par session | Gratuit | les mêmes que vous payez actuellement. |
| Temps de déplacement | Temps de déplacement | Temps de déplacement |
| 43,75min. | 70 min. | les mêmes que vous payez actuellement. |
L’analyse statistique de ces données de choix repose sur l’estimation d’un modèle multinomial logit à effet aléatoire. Cette analyse de l’arbitrage entre le temps et le coût monétaire permet de déterminer la valeur du temps, qui peut varier en fonction des modes de transport et des caractéristiques des répondants. Les résultats de l’étude suggèrent une valeur moyenne du temps de 4 $ de l’heure pour les déplacements en voiture et de 6 $ de l’heure en autobus.
16.1.3 Consensus et défis concernant la valeur du temps
Il existe un grand nombre d’études empiriques visant à déterminer la VT, principalement dans le contexte du transport. Boardman et al., (2018) ainsi que le Victoria Transport Policy Institute (s.d.) proposent des synthèses à ce sujet. De plus, plusieurs méta-analyses ont été réalisées sur ce thème, notamment par Abrantes et Wardman (2011) pour le Royaume-Uni et par Wardman et al., (2016) pour l’Europe. En revanche, les études canadiennes sur la VT sont rares.
Certains consensus émergent des recherches sur la VT :
- La VT dépend positivement et fortement du niveau de revenu. En pratique, elle est souvent exprimée comme une fraction du salaire brut, ce qui suppose implicitement une élasticité de la VT par rapport au revenu unitaire. La méta-analyse de Wardman et al., (2016) confirme que cette hypothèse est réaliste ;
- Le motif de déplacement constitue un déterminant important de la VT. Il est essentiel d’établir une distinction entre les déplacements liés aux affaires et les autres déplacements, tels que les trajets domicile-travail, les déplacements de loisirs ou pour d’autres motifs ;
- La VT augmente avec la distance du déplacement, avec une élasticité estimée entre 0,1 et 0,2. Cependant, cette relation n’est probablement pas linéaire. De nombreuses études distinguent entre les déplacements locaux et les déplacements interurbains ;
- Les conditions de déplacement, telles que l’attente ou la congestion, jouent également un rôle important dans la détermination de la VT ;
- Le mode de transport influence la VT, mais il est difficile de distinguer l’effet spécifique du mode de transport de celui de la composition socioéconomique de la clientèle de chaque mode. Par exemple, la valorisation plus élevée du temps économisé en avion est probablement due en partie au fait que les passagers aériens ont généralement un revenu moyen plus élevé ;
- La VT semble être plus élevée en Europe qu’en Amérique du Nord ;
- Le niveau de confort d’un mode de transport en commun influe sur la valeur du temps, et le taux de remplissage des véhicules constitue l’un des éléments essentiels de ce confort ;
- La fiabilité du temps de déplacement est également un élément pour lequel il existe une valeur spécifique pour laquelle les individus sont prêts à payer.
Plusieurs autorités ont adopté des directives précises concernant la valorisation du temps dans le cadre de projets de transport. Par exemple, en France, Baumstark et al. (2013) consacre deux chapitres à ce sujet. Au Royaume-Uni, le Département des Transports émet des directives détaillées sur les valeurs du temps à utiliser pour les projets de transport (voir le Transport Analysis Guidance).
Au Canada, Zhang et al., (2004) ont réalisé une revue des connaissances sur la valeur du temps dans le domaine du transport[1]. Leurs principales recommandations sont résumées dans le Tableau 16.2. Parmi celles-ci, ils recommandent notamment l’utilisation de facteurs d’ajustements en cas de congestion, pour les déplacements à pied ou en cas d’attente. Ces ajustements reflètent la désutilité de ces situations.
| Élément | VT recommandée |
| Déplacements privés (loisirs et trajet domicile-travail) | 50 % du salaire net |
| Déplacements d’affaires (payés par l’employeur) | Le salaire brut plus les autres avantages sociaux |
| Déplacement en période de congestion | 2 x VT |
| Déplacement à pied | 2 x VT |
| Temps d’attente | 2,5 x VT |
| Élasticité VT par rapport au revenu | 0,75 |
| Élasticité VT par rapport à la distance | 0,3 |
| Source : S’appuie sur les recommandations de Zhang et al., (2004). | |
Il convient de préciser que les innovations technologiques, notamment la connectivité, ont probablement entraîné une réduction de la valeur du temps, en particulier pour les modes de transport qui ne nécessitent pas une attention constante. En effet, les temps de déplacement peuvent désormais être utilisés pour travailler en ligne ou se divertir, grâce aux nouvelles technologies (voir ITF, 2019).
16.2 La valeur statistique d’une vie
16.2.1 La définition et l’utilisation du concept
La réduction des risques de mortalité constitue souvent un résultat de projets dans les domaines de la santé, du transport, de la sécurité ou de l’environnement. Pour évaluer cet avantage, il est nécessaire d’établir une valeur de la vie humaine. Bien que cela puisse sembler délicat au point de vue éthique, il est important de souligner qu’il ne s’agit pas de mettre une valeur sur la vie d’une personne spécifique face à une mort certaine.
La valeur statistique d’une vie (VSV) mesure le consentement à payer pour réduire le risque de mortalité prématurée. Par convention, elle est exprimée sous la forme de la volonté à payer pour sauver une vie, même si dans la réalité, elle repose sur le consentement à payer pour une petite réduction du risque de mortalité.
Exemple : La VSV et le risque d’une maladie mortelle
Le consentement à payer maximal pour éliminer le risque de mortalité prématurée liée à une maladie a été évalué à 200 $ par an et par personne exposée. On sait également que le risque de décès prématuré causé par cette maladie est de 1 sur 10 000, et que la population exposée à ce risque est de 200 000 personnes. Déterminez la VSV dans cette situation.
Réponse
- Le consentement total à payer de la population = 200 $ x 200 000 = 40 millions de dollars;
- Le nombre de vies sauvées en moyenne par an =[latex]\frac{1}{10\ 000} \times 200\ 000[/latex] = 20 ;
- La VSL est donc, dans cet exemple, de [latex]\frac{40 \text{ millions}}{20}[/latex] = 2 millions de dollars.
Une méthode alternative de résolution consiste à diviser le consentement individuel par la réduction du risque, soit :
[latex]\frac{200\$}{(\frac{1}{10 \ 000})}[/latex] = 2 millions de dollars
Le concept de VSV est aujourd’hui largement utilisé aux États-Unis et dans d’autres juridictions pour évaluer les avantages des interventions qui modifient les risques de mortalité prématurée. Cela permet d’apporter une certaine cohérence à nos choix collectifs et de réduire l’arbitraire dans les décisions politiques.
À cet égard, Viscusi et al., (1997) ont calculé la VSV implicite de différentes réglementations en matière de santé et de sécurité adoptées aux États-Unis dans les années 1970 et 1980, soit avant l’obligation d’effectuer des ACA. Leurs résultats révèlent des valeurs de VSV implicites très variables. Par exemple, certaines réglementations, telles que l’obligation d’installer des sacs gonflables dans les automobiles, ont permis de sauver des vies à de faibles coûts (environ 100 000 $ par vie sauvée en dollars de 1984). En revanche, d’autres réglementations impliquaient une VSV de plus d’un milliard de dollars (par exemple, les limites d’exposition au formaldéhyde en milieu de travail en 1987).
16.2.2 La détermination empirique de la VSV
Historiquement, la valeur statistique de la vie (VSV) s’établissait sur la base de la contribution nette d’un individu à la richesse collective. Par exemple, le coût associé à un décès prématuré s’évaluait en calculant le revenu net de la consommation qu’un individu aurait pu générer s’il avait eu une durée de vie normale.
Cette approche a cependant été critiquée, car elle aboutissait à des résultats discutables, notamment avec des valeurs négatives pour certains individus, et elle ne reflétait pas le concept de consentement à payer pour réduire les risques.
Aujourd’hui, l’évaluation de la VSV s’établit à partir de techniques plus sophistiquées, comme celles qui ont été exposées dans les chapitres précédents. Les prochains paragraphes décrivent brièvement certaines applications de ces techniques.
La méthode hédonique des salaires
La méthode hédonique des salaires, initialement proposée par Thaler et Rosen (1975), consiste à estimer une équation de salaire ou équation de Mincer de la forme suivante :
[latex]\ ln(w_{i,j,k})=\alpha + \beta \text{Risque}_{j,k} + \gamma X_{i,j,k} + \epsilon_{i,j,k}[/latex]
où :
[latex]w_{i,j,k}[/latex]: le salaire horaire du travailleur i employé dans l’industrie j dans une occupation k ;
[latex]\text{Risque}_{j,k}[/latex]: le risque de mortalité d’un accident de travail dans l’industrie j et l’occupation k. Cette variable provient souvent des statistiques officielles et se mesure en nombres annuels de décès liés au travail par 100 000 travailleurs ;
[latex]X_{i,j,k}[/latex]: un ensemble de variables qui déterminent le niveau de revenu (telles que l’âge, le sexe, le niveau d’éducation, d’expérience, les conditions de travail, etc.) ;
[latex]\epsilon_{i,j,k}[/latex]: un terme d’erreur aléatoire qui capte les éléments influençant le salaire, mais qui ne sont pas observables ;
[latex]\alpha , \beta , \gamma[/latex]: les paramètres à estimer à partir des données et de techniques statistiques appropriées.
L’estimation doit s’effectuer sur des données comprenant suffisamment d’observations pour permettre d’établir la prime salariale nécessaire pour compenser une unité supplémentaire de risque, toutes autres choses étant égales par ailleurs. Dans ce contexte, il s’agit d’évaluer le consentement à recevoir.
L’estimation de l’équation de salaire pose différents défis économétriques que nous ne décrivons pas ici. Une fois le paramètre estimé, la VSV s’obtient comme suit[2] :
[latex]VSV= \beta \times w \times h \times 100\ 000[/latex]
avec h représentant le nombre d’heures de travail par année.
En s’appuyant sur cette approche, Kniesner et al., (2012) ont estimé une équation de salaire à partir de données américaines concernant 2 036 hommes observés à plusieurs reprises entre 1993 et 2001. Le risque moyen annuel dans leur échantillon est de 6,4 décès par 100 000 travailleurs. Leur analyse économétrique a révélé une VSV comprise entre 4 et 10 millions de dollars US.
Les principales critiques de cette approche sont les suivantes :
- Risque de biais de sélection : Les personnes qui choisissent des métiers risqués peuvent manifester une aversion au risque moindre que les autres membres de la population. Dans ce cas, la prime salariale qu’elles reçoivent sous-estime le consentement à payer pour réduire le risque dans la population en général ;
- Niveau d’information sur les risques : Si les travailleurs possèdent une connaissance imparfaite des risques, leur salaire peut ne pas refléter de manière adéquate le risque objectif ;
- Imperfections du marché du travail : Des distorsions telles que la présence de syndicats ou le pouvoir de monopsone peuvent faire en sorte que les primes de risque versées ne reflètent pas fidèlement la valeur statistique de la vie ;
- Autres risques : Les primes salariales peuvent également compenser d’autres types de risques, tels les accidents non mortels entraînant des blessures ou une invalidité. Comme les risques de ces différents types d’événements sont souvent fortement corrélés, il est difficile de distinguer la prime liée au risque de décès de celle compensant les autres risques.
Ces critiques soulignent les limites et les défis associés à l’utilisation de l’approche hédonique des salaires pour estimer la valeur statistique de la vie.
La méthode hédonique sur des biens durables
La méthode hédonique peut également être appliquée à des biens durables dont la valeur est influencée par le risque de mortalité. Par exemple, certaines analyses étudient la valeur des maisons en fonction des risques de mortalité dans le quartier. Gayer, Hamilton et Viscusi (2000) ont obtenu une VSV de 7,2 millions de dollars américains en examinant le lien existant entre la valeur des propriétés et la proximité d’un site chimique contaminé, ce qui accroît la probabilité de mortalité par le cancer.
De plus, certaines études estiment la VSV à partir de régressions hédoniques du prix des automobiles, car certains véhicules sont plus sécuritaires que d’autres. Par exemple, Rohlfs, Sullivan et Kniesner (2015) ont inféré une VSV de 9 à 10 millions de dollars américains sur la base de la prime accordée aux automobiles qui disposaient de sacs gonflables, à la fin des années 1990.
Les dépenses d’évitement
Les dépenses pour des achats de biens ou de services motivés directement par la réduction du risque de mortalité permettent de déduire la VSV. Par exemple, si l’achat d’un supplément alimentaire coûte 25 $ par année et que son seul avantage consiste à réduire le risque annuel de mortalité d’une personne sur 100 000, cela implique une VSV d’au moins 2,5 millions de dollars pour les personnes qui achètent ce produit.
Cependant, les biens et les services de sécurité procurent souvent d’autres avantages, tels la prévention de maladies non mortelles, ce qui rend l’analyse un peu plus complexe. La VSV a été déduite notamment en analysant les dépenses pour l’achat de casques de vélo (Jenkins, Owens et Wiggings, 2001), de détecteurs d’incendie (Garbacz, 1989) et pour l’achat de nourriture bio pour les bébés (Maguire et al., 2004).
Les approches fondées sur les préférences déclarées
L’évaluation contingente et autres méthodes connexes sont de plus en plus utilisées pour établir la VSV (Kniesner et Viscusi, 2019, OCDE, 2012). Le principe de ces méthodes consiste à demander à un échantillon représentatif de la population combien les répondants seraient prêts à payer pour réduire leur risque de décès. Toutefois, le défi majeur de ces méthodes réside dans la nécessité de rendre les choix présentés aussi compréhensibles et réalistes que possible.
Au Canada, les études utilisant des données de préférence déclarées sont encore relativement rares, et la plupart d’entre elles datent. À titre d’exemple, nous pouvons mentionner l’étude de Chestnut, Rowe et Breffle (2012), résumée dans l’encadré ci-dessous.
Le cancer ou l’accident cardiaque et la VSV au Canada et aux États‑Unis
 Chesnut, Rowe et Breffle (2012) ont mené deux enquêtes en ligne auprès d’adultes âgés de 35 à 84 ans, l’une avec 885 répondants américains et l’autre avec 641 répondants canadiens (à l’exception du Québec). Ces enquêtes visaient à évaluer le consentement à payer pour réduire le risque de mortalité annuelle de 1, 2 et 5 pour 10 000 par cancer ou par défaillance cardiaque. Les participants devaient envisager un paiement hypothétique pour participer à des activités de prévention coûteuses, telles que des tests de dépistage annuels non couverts par l’assurance ou l’achat de suppléments et de produits naturels. Les questionnaires précisaient que ces programmes ne présentaient pas d’effets secondaires, et que les répondants devraient payer chaque année pendant le reste de leur vie pour bénéficier des effets escomptés.
Chesnut, Rowe et Breffle (2012) ont mené deux enquêtes en ligne auprès d’adultes âgés de 35 à 84 ans, l’une avec 885 répondants américains et l’autre avec 641 répondants canadiens (à l’exception du Québec). Ces enquêtes visaient à évaluer le consentement à payer pour réduire le risque de mortalité annuelle de 1, 2 et 5 pour 10 000 par cancer ou par défaillance cardiaque. Les participants devaient envisager un paiement hypothétique pour participer à des activités de prévention coûteuses, telles que des tests de dépistage annuels non couverts par l’assurance ou l’achat de suppléments et de produits naturels. Les questionnaires précisaient que ces programmes ne présentaient pas d’effets secondaires, et que les répondants devraient payer chaque année pendant le reste de leur vie pour bénéficier des effets escomptés.
Le consentement à payer a été évalué à l’aide de quatre choix binaires, dans lesquels les participants devaient choisir entre la réduction du risque et le coût à payer. Certains choix comprenaient le statu quo comme option, c’est‑à-dire aucune réduction du risque ni du coût supplémentaire.
En plus de ces choix binaires, les répondants devaient indiquer leur consentement maximal à payer pour réduire leur risque de mortalité par cancer ou accident cardiaque à l’aide d’une carte de paiement de 0 $ à 6 200 $ par année. Pour aider les répondants à comprendre les choix proposés, le questionnaire commençait par une présentation des risques réels de mortalité par cancer et par accident cardiaque en fonction de l’âge, suivie de questions visant à vérifier la compréhension des participants.
L’analyse statistique a examiné l’effet de plusieurs facteurs explicatifs sur le consentement à payer, notamment la nature du risque (cancer ou accident cardiaque), l’importance de la réduction du risque, l’âge, le revenu du ménage, une estimation de la qualité de vie attendue au cours des 10 prochaines années, l’attitude face au risque et la présence d’enfants.
Les principaux résultats de l’analyse des choix binaires sont les suivants :
- Le consentement à payer augmente avec l’importance de la réduction du risque, et l’élasticité est estimée à 0,3 ;
- Il n’existe aucune prime spécifique pour éviter le cancer, le consentement à payer ne dépend donc pas de la cause de la mortalité ;
- L’élasticité du consentement à payer par rapport au revenu s’estime à environ 0,5 ;
- L’âge n’a aucun effet statistiquement significatif sur le consentement à payer pour réduire les risques de mortalité ;
- L’aversion au risque des répondants a un effet positif sur le consentement à payer ;
- Les résultats pour le Canada et les États-Unis sont très semblables ;
- L’analyse des déterminants du CAP obtenus à partir de la carte de paiement a donné des résultats assez semblables, à quelques exceptions près. Par exemple, l’âge semble produire un effet positif sur le consentement à payer, dans cette approche.
La valeur statistique de la vie humaine (VSV) estimée à partir des choix binaires se situe entre 4 et 5 millions de dollars américains de 2012. En revanche, la valeur estimée à partir des réponses obtenues avec une carte de paiement s’avère deux fois moins élevée. Les auteurs suggèrent que les répondants peuvent accorder moins d’importance au coût dans l’approche par choix binaires, car celle-ci exige du répondant de traiter plus d’informations.
Le transfert de valeur
Le transfert de valeur constitue une approche particulièrement pertinente pour évaluer la VSV, car de nombreuses estimations de la VSV existent déjà dans divers contextes et ont été obtenues à l’aide de différentes méthodes. Plusieurs méta-analyses ont été réalisées pour analyser les facteurs contextuels susceptibles d’influencer cette valeur. Parmi les ajustements habituels figurent le taux de change et le niveau de revenu. En ce qui concerne ce dernier point, plusieurs études se sont penchées sur la manière dont la VSV évolue en fonction du revenu. La prochaine section abordera l’état actuel des connaissances sur la VSV, en mettant notamment l’accent sur sa relation avec le revenu.
16.2.3 L’état des connaissances et les défis concernant la valeur statistique d’une vie humaine
Les estimations de la VSV varient considérablement d’une étude à l’autre. Par exemple, l’OCDE a réalisé une méta-analyse portant sur 856 évaluations de la VSV fondées sur des données de préférences déclarées. Parmi ces évaluations, 32 % ont attribué une valeur inférieure à 1 million de dollars américains de 2005, 24 % se situent entre 1 et 3 millions, et 15 % dépassent les 20 millions de dollars.
Les balises utilisées par différentes agences officielles présentent également des variations importantes. Par exemple, selon Robinson et al. (2010), les valeurs utilisées par les organismes de réglementation américains pour la VSV varient de 1 à 21 millions de dollars américains de 2007. De son côté, la Commission européenne recommande une fourchette de 1 à 2 millions d’euros de 2000. Au Canada, le Guide d’analyse coût‑avantages pour le Canada de 2023 recommande une valeur de 6,5 millions de dollars canadiens (de 2007), ajustée en fonction de l’inflation. Au Québec, Rojas et al. (2023) propose deux estimations distinctes de la VSV. La première, évaluée à 4,1 millions de dollars, est dérivée en utilisant la méthode de la disposition à payer. La seconde, quant à elle, est fixée à 2,6 millions de dollars et est calculée d’après la méthode du capital humain. Ces valeurs sont exprimées en dollars canadiens de l’année 2019.
Sur la base des résultats d’une méta-analyse, l’OCDE (2012) formule les recommandations suivantes :
- Au sein d’une même juridiction, il est recommandé, pour des raisons éthiques, d’utiliser la même valeur statistique de la vie pour tous les individus, indépendamment de leurs revenus. Ainsi, il convient d’éviter d’appliquer une VSV moindre à des projets affectant des personnes à faible revenu ;
- Cependant, il est conseillé d’ajuster la VSV en fonction du revenu moyen de la juridiction. Par exemple, il est normal que le Québec utilise une VSV moins élevée que les États-Unis, étant donné que le niveau de vie y est inférieur. En cas d’utilisation de la méthode de transfert de valeur, l’OCDE recommande d’appliquer une valeur d’élasticité du revenu de 0,8 pour les pays développés, avec une analyse de sensibilité à 0,4. Il est également recommandé d’ajuster la VSV en fonction de la croissance économique d’une juridiction ;
- Il n’existe pas de preuves solides indiquant que le consentement à payer pour réduire le risque diminue avec l’âge. Par conséquent, il est inapproprié de réduire la VSV en fonction de l’âge. En revanche, il semble que le consentement à payer pour réduire les risques de mortalité des enfants soit plus élevé, ce qui pourrait justifier l’ajout d’une prime pour les enfants ;
- Les preuves disponibles ne permettent pas non plus d’établir de lien clair entre la nature du risque et la VSV. Certaines études suggèrent l’existence d’une prime pour éviter certains risques, tels que le cancer, mais les résultats restent trop fragmentaires pour recommander des ajustements spécifiques.
Les défis de la VSV
En plus des limites associées aux méthodes d’estimation mentionnées précédemment, le concept et l’utilisation de la VSV posent d’autres enjeux (Bosworth, Hunter et Kibria, 2017).
1. Une mesure fondée sur une faible variation de risque
Durant la pandémie de COVID-19, le concept de VSV a été utilisé pour effectuer des ACA de différentes politiques publiques, telles que la distanciation sociale (par exemple, Thunström et al., 2020). L’utilisation de la VSV dans ce contexte a été contestée (Colmer, 2020), car cette valeur est déterminée sur la base de petites variations du risque de mortalité et non pour des contextes comme le COVID-19, alors que les risques s’avéraient importants.
2. Des biais cognitifs dans la perception des risques
Les méthodes s’appuyant sur les préférences déclarées sont particulièrement sensibles aux biais cognitifs. Des recherches ont montré que les individus ont tendance à surévaluer les risques faibles tels que l’écrasement d’un avion ou un acte terroriste, tandis qu’ils ont tendance à sous-évaluer les risques plus courants, tels que la mortalité liée aux accidents de voiture ou à la surconsommation d’aliments industriels.
De plus, il semble qu’il existe une aversion à l’ambiguïté, c’est-à-dire une préférence pour des situations où les risques sont connus plutôt que mal définis. Cette aversion pour l’ambiguïté peut conduire à une surestimation de la valeur statistique de la vie lorsqu’elle est établie à partir de risques mal définis.
3. Les biais dans le processus de publication
Pour les chercheurs, il est plus probable de publier des résultats qui sont élevés, statistiquement significatifs et qui confortent les consensus établis. Par conséquent, il est possible que les études qui obtiennent des valeurs faibles de la VSV ne soient pas retenues ni même soumises pour publication.
Pour évaluer ces enjeux, certaines méta-analyses pondèrent les observations en fonction de leur écart-type, ce qui signifie qu’une estimation de la VSV avec un écart-type faible aura plus de poids. Cette correction semble aboutir à une réduction parfois importante de la VSV (Doucouliagos et al., 2012).
4. Le risque d’instrumentalisation
Enfin, le choix de la valeur de la VSV dans un contexte où il existe une fourchette importante de valeurs crée un risque d’instrumentalisation. Les analystes peuvent avoir intérêt à sélectionner une VSV élevée pour justifier le plus d’interventions réglementaires possibles, ce qui peut influencer les décisions politiques et l’allocation de ressources.
16.3 Le coût social du carbone
La lutte contre les changements climatiques est devenue une préoccupation majeure des politiques publiques au cours des dernières décennies. Dans ce contexte, l’analyse des politiques climatiques nécessite l’évaluation de la valeur d’une tonne de carbone émise, ou au contraire, réduite ou évitée.
Le coût social du carbone (CSC) (social cost of carbon) constitue une mesure monétaire des dommages présents et futurs engendrés par l’émission d’une tonne supplémentaire de dioxyde de carbone (CO2) dans l’atmosphère lors d’une année donnée.
Il est important de souligner les aspects suivants de cette définition :
- Le CSC vise à évaluer les dommages à l’échelle mondiale ;
- En raison de la durée du cycle du carbone, l’horizon temporel pris en compte s’étend sur 100 ans ou plus. Par conséquent, le choix du taux d’actualisation social pour agréger les impacts dans le temps revêt une importance capitale ;
- Le CSC est un coût marginal, car il correspond au coût engendré par une tonne supplémentaire de CO2, compte tenu du stock de carbone déjà présent dans l’atmosphère. Cette caractéristique implique que le CSC augmente avec le temps, car la quantité totale de carbone dans l’atmosphère, et donc les dommages marginaux, augmentent année après année.
L’intégration des dommages mondiaux dans l’évaluation du coût social du carbone (CSC) entraîne souvent une asymétrie spatiale dans l’évaluation des avantages et des coûts des projets liés aux changements climatiques. Par exemple, tandis que les coûts d’un programme de réduction des émissions de gaz à effet de serre peuvent être uniquement calculés au niveau national, les avantages sont souvent estimés à l’échelle mondiale.
Il convient néanmoins de rappeler que l’Organisation de coopération et de développement économiques (OCDE) recommande de prendre en compte les impacts internationaux lorsque des traités internationaux exigent le contrôle de ces effets, ou lorsque des considérations éthiques le justifient (voir Chapitre 2).
L’évaluation du CSC est complexe et comporte une grande part d’incertitude. Au Canada, le CSC utilisé par le gouvernement fédéral est établi sur la base de la méthode du transfert, à partir de recommandations effectuées aux États‑Unis. L’ajustement principal concerne la conversion en dollars canadiens. La dernière mise à jour date de décembre 2022.
Les recommandations américaines utilisées par Environnement Canada ont été établies en 2009 sous la présidence d’Obama par un groupe de travail interdépartemental, avec des mises à jour en 2016 et en 2021. Jusqu’à la dernière mise à jour, les évaluations s’appuyaient sur des estimations provenant de trois modèles d’évaluations intégrés : les modèles DICE, PAGE et FUND, qui sont brièvement présentés dans l’encadré ci-dessous. Depuis 2021, le coût social du carbone (CSC) est évalué à partir d’un modèle d’évaluation intégré qui incorpore les avancées scientifiques les plus récentes (US EPA, 2023).
Les modèles d’évaluation intégrés
Les modèles d’évaluation intégrés sont des modèles multidisciplinaires qui lient un modèle économique à des modèles du climat, de l’atmosphère, des océans et du cycle du carbone, entre autres. La Figure 16.1 illustre la structure générale de ces modèles.
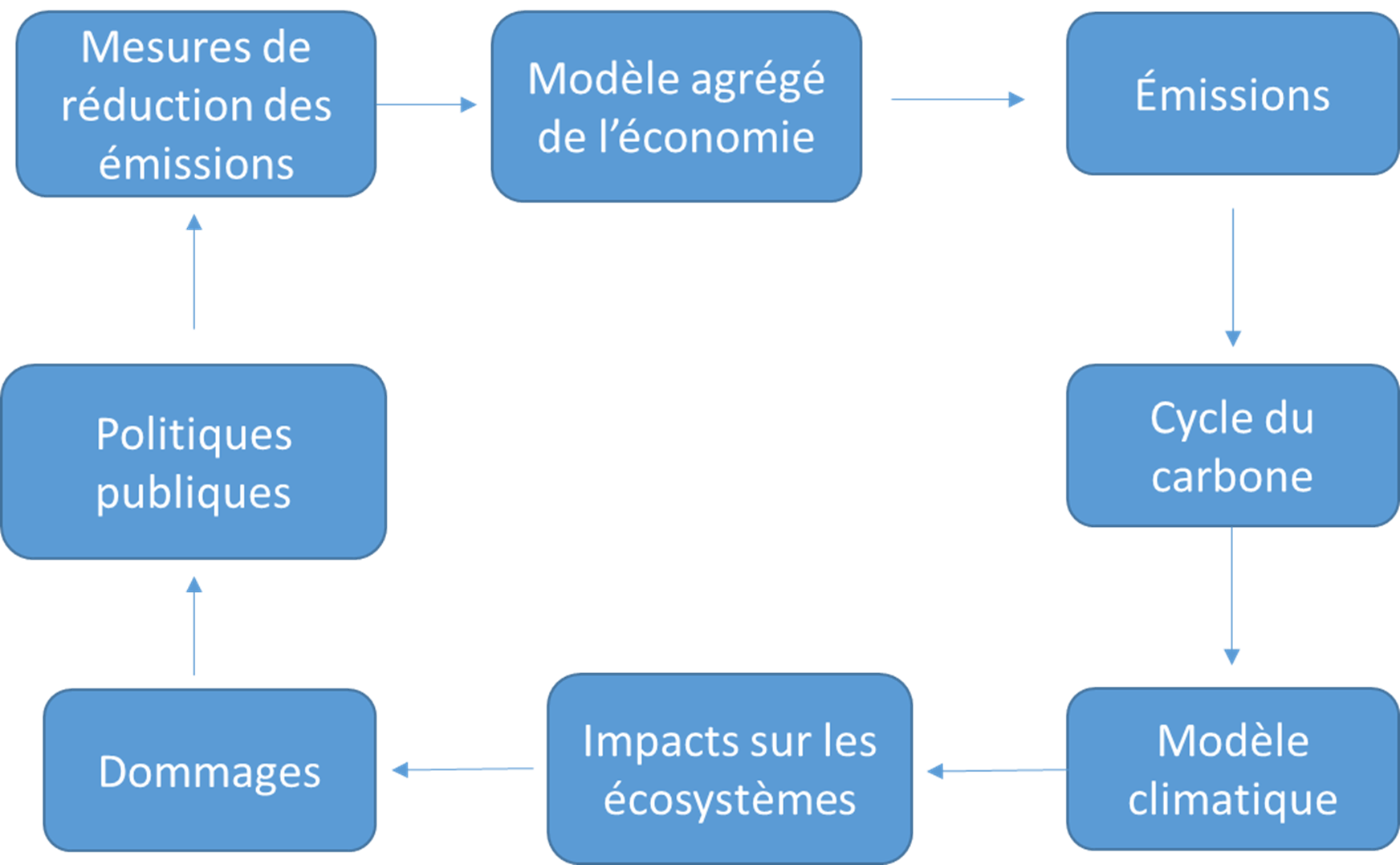
Il s’agit de modèles probabilistes dans lesquels les valeurs des paramètres proviennent de distribution de probabilités. Selon Metcalf et Stock (2017), les principales sources de variations entre les modèles sont : la sensibilité du climat à la concentration de CO2, les fonctions de dommages, le traitement des événements peu probables, mais catastrophiques, et le taux d’actualisation.
La fiabilité de ces modèles est remise en question par certains, comme par l’économiste Robert Pindyck.
A plethora of integrated assessment models (IAMs) have been constructed and used to estimate the social cost of carbon (SCC) and evaluate alternative abatement policies. These models have crucial flaws that make them close to useless as tools for policy analysis: certain inputs (e.g., the discount rate) are arbitrary, but have huge effects on the SCC estimates the models produce; the models’ descriptions of the impact of climate change are completely ad hoc, with no theoretical or empirical foundation; and the models can tell us nothing about the most important driver of the SCC, the possibility of a catastrophic climate outcome. IAM-based analyses of climate policy create a perception of knowledge and precision, but that perception is illusory and misleading.
Source : Pindyck, 2013, p. 860
DICE
Le modèle DICE, pour « Dynamic Integrated model of Climate and The Economy », a été créé par le lauréat du prix Nobel d’Économie 2018, William Nordhaus. Il s’agit d’un modèle d’évaluation intégré qui vise à évaluer les politiques climatiques en prenant en compte les interactions entre l’économie, le cycle du carbone, les changements climatiques et les politiques publiques. DICE est un modèle néoclassique de croissance, dans lequel les émissions de gaz à effets de serre (GES) entraînent un impact négatif sur le capital naturel. Les investissements dans la réduction des GES entraînent une réduction de la consommation actuelle, mais permettent d’éviter des dommages futurs. Les recommandations en matière de politique climatique sont établies à partir d’un processus d’optimisation non linéaire d’une fonction de bien-être social.
FUND
Le modèle FUND, qui signifie « Climate Framework for Uncertainty, Negociation and Distribution », intègre des scénarios et des modèles simples de la population, de la technologie, de l’économie, des émissions, de la chimie de l’atmosphère, du climat et du niveau des mers. Ce modèle prend en compte 16 régions dans le monde et couvre la période de 1950 à 2300. Initialement développé par l’économiste néerlandais Richard Tol, le modèle FUND a été largement utilisé par le Groupe d’experts intergouvernemental sur l’évolution du climat (GIEC ou IPCC en anglais). Il est connu pour produire souvent des CSC plus bas que les modè DICE et PAGE.
PAGE
Le modèle PAGE, qui signifie « Policy Analysis of the Greenhouse Effect », a été créé par Chris Hope de l’Université de Cambridge. Ce modèle couvre dix périodes de 2000 à 2200 et divise le monde en 9 régions. Il s’agit d’un modèle stochastique dans lequel les principaux paramètres sont définis par des distributions de probabilités. Le modèle intègre des dommages économiques et non économiques, ainsi que la possibilité d’effets catastrophiques liés aux changements climatiques.
Le modèle PAGE a été utilisé comme base pour l’ACA des changements climatiques dans le rapport Stern de 2007, qui a été commandé par le gouvernement britannique. Dans ce contexte, un taux d’actualisation de 1,4 % a été utilisé. Le modèle prend également en compte des aspects d’équité, en tenant compte de l’utilité marginale décroissante de la consommation.
Le Tableau 16.3 présente une sélection des valeurs recommandées par Environnement Canada (2023) pour le coût social du carbone [3]. Il est important de noter que le prix du carbone établi par le système québécois de plafonnement et d’échange de droits d’émission ne correspond pas nécessairement au CSC. En effet, ce prix dépend de la quantité de permis mis en marché par le gouvernement. Il ne sera égal au CSC que si la quantité de permis correspond au niveau d’émissions socialement optimales [4].
| Année | CSC/CS-CO2 |
| 2020 | 247 |
| 2021 | 252 |
| 2022 | 256 |
| 2023 | 261 |
| 2024 | 266 |
| 2025 | 271 |
| 2030 | 294 |
| 2040 | 341 |
| 2050 | 394 |
| Source : Environnement et changement climatique Canada (2023) |
|
16.4 Conclusions
Éléments clés à retenir
- La valeur du temps est un paramètre utilisé fréquemment dans les ACA dans le domaine des transports.
- Elle mesure le consentement à payer pour épargner du temps lors d’un déplacement.
- Cette valeur est liée au salaire, mais elle dépend également des préférences et des conditions du déplacement.
- La détermination empirique de la valeur du temps s’effectue en analysant des choix réels ou hypothétiques qui traduisent un compromis entre le temps et les coûts monétaires.
- De nombreuses études ont été menées sur la valeur du temps et ses déterminants, ce qui permet d’envisager l’utilisation de la méthode de transfert.
- Bien que la valeur statistique d’une vie s’exprime sous la forme du consentement à payer pour éviter un décès, elle s’appuie en fait sur la mesure de la volonté à payer pour une petite réduction du risque de décès.
- La valeur de la vie peut être évaluée à partir de la méthode hédonique du salaire, des biens durables ou des dépenses d’évitement. Les méthodes directes sont cependant de plus en plus utilisées.
- Les évaluations de la valeur de la vie sont très variables, mais elles sont le plus souvent comprises entre 5 à 10 millions de dollars dans les pays développés. Cette valeur augmente avec le niveau de vie d’un pays.
- Il n’est pas justifié sur le plan empirique de réduire la valeur de la vie avec l’âge, mais une prime pour les enfants peut être justifiée.
- Le coût social du carbone mesure la valeur des dommages actuels et futurs totaux engendrés par l’émission d’une tonne supplémentaire de carbone.
- Il s’agit d’un paramètre important pour les ACA des politiques climatiques.
- L’évaluation de la valeur du coût social du carbone s’appuie sur des modèles d’évaluation intégrés complexes.
- Il existe beaucoup d’incertitude sur l’évaluation de ce paramètre, et sa valeur dépend notamment du taux d’actualisation utilisé pour additionner les dommages dans le temps.
- Plusieurs juridictions statuent sur les valeurs qui doivent être utilisées dans les ACA des politiques publiques.
Retour sur la motivation
Un gouvernement envisage d’augmenter la limite de vitesse de ses autoroutes de 100 km/h à 120 km/h. Les principaux impacts à évaluer dans une ACA de ce projet sont les suivants :
- Les gains de temps engendrés par l’augmentation de la vitesse ;
- Les impacts sur la sécurité routière, étant donné que ce projet pourrait augmenter les risques d’accidents et de mortalité sur les routes ;
- Les impacts sur l’environnement, notamment en ce qui concerne les changements climatiques.
Cette ACA nécessiterait donc d’établir des « prix de référence », notamment pour une heure de temps de déplacement économisé, pour une vie humaine et pour une tonne de carbone. Comment les méthodes présentées dans les chapitres précédents permettent-elles de déterminer ces valeurs ?
Résolution
Le but principal de ce chapitre est de répondre aux interrogations soulevées dans cet exemple. En outre, Van Benthem (2015) examine les avantages et les coûts sociaux associés à l’augmentation de la limite de vitesse de 55 à 65 mi/h sur les autoroutes de l’ouest des États-Unis entre 1987 et 1996. Selon cette analyse, une augmentation de 10 mi/h de la limite de vitesse entraîne une augmentation de la vitesse réelle de 3 à 4 mi/h, ce qui engendre une augmentation des accidents de 9 à 15%, avec des conséquences souvent mortelles. Cette augmentation de la vitesse est également associée à une détérioration de la pollution atmosphérique, ayant des impacts significatifs sur la santé publique.
Ainsi, les coûts sociaux résultant de cette augmentation de vitesse sont estimés être de deux à sept fois supérieurs aux avantages sociaux. L’auteur soutient également que cette conclusion reste valable même en prenant en compte les performances des véhicules plus récents.
Exercices
1.(*) Pour dissoudre un caillot sanguin lors d’une crise cardiaque, le médicament actuellement utilisé comporte un risque de 5 sur 100 000 cas de réactions allergiques mortelles. Les autorités sanitaires évaluent l’utilisation d’un nouveau médicament plus dispendieux, mais qui réduit le risque de réactions mortelles à 3 cas sur 100 000. Pour le reste, ces deux médicaments sont équivalents. Les autorités utilisent comme balise dans les décisions d’approbation des nouveaux médicaments une valeur statistique de la vie de 5 millions de dollars. Dans ces conditions, pour être accepté en fonction de la balise, le coût supplémentaire du nouveau médicament peut être au maximum de :
a) 40 $ ;
b) 55 $ ;
c) 75 $ ;
d) 100 $ ;
e) 150 $;
f) 175 $ ;
g) 250 $ ;
h) Aucune des réponses ci-dessus.
2. Quel est le rôle du coût social du carbone dans l’évaluation des investissements et des projets à faible émission de carbone ?
3. (*) Aux États-Unis, l’administration Trump (2017-2021) a revu la méthode de calcul du coût social du carbone proposée par l’administration Obama (2009‑2017). Les deux principaux changements apportés à cette méthode ont été les suivants : i) la considération des dommages exclusivement aux États‑Unis plutôt que des dommages mondiaux ; ii) l’utilisation d’un taux d’actualisation de 7 à 10 %, au lieu du taux de 3 %. Expliquez comment ces changements ont pu affecter la valeur attribuée au coût social du carbone. Discutez du bien-fondé de ces changements.
4. Concernant le concept de valeur du temps épargné, veuillez brièvement répondre aux questions suivantes :
a) Comment la valeur du temps épargné est-elle généralement mesurée et exprimée ?
b) Pourquoi la valeur du temps épargné n’est-elle pas toujours égale au salaire net ?
c) Comment la valeur du temps épargné varie-t-elle selon le mode de transport (voiture, transport en commun, marche, etc.) et selon le type de déplacement (travail, loisirs, courses, etc.) ?
Annexe 1
Les données récoltées sur les choix réels ou hypothétiques présentent le plus souvent un caractère discret, c’est-à-dire que la variable à expliquer (par exemple, le choix du mode de transport) ne constitue pas une variable continue, mais plutôt une variable ayant un nombre limité de valeurs. Par exemple, si un travailleur a le choix entre se rendre au travail en voiture, en autobus ou par un mode non motorisé, la variable « choix de mode de transport » comprend trois valeurs possibles, par exemple 1 = voiture, 2 = autobus et 3 = mode non motorisé. L’analyse économétrique des variables discrètes exige l’utilisation de techniques particulières – l’économétrie des choix discrets – dont la présentation détaillée dépasse le cadre de ce manuel. Mentionnons simplement que ces techniques sont souvent fondées sur le modèle de l’utilité aléatoire additive introduite par McFadden (1974). Dans ce modèle, on suppose qu’un individu i effectue un choix de mode de transport en comparant le niveau d’utilité qu’il obtiendrait avec chaque mode, selon la fonction suivante :
[latex]U_{im}=V_{im} + \epsilon _{im}[/latex]
avec :
i : l’indicateur du répondant.
m : l’indicateur du mode (m = 1 pour la voiture, m = 2 pour l’autobus et m = 3 pour un mode non motorisé).
[latex]V_{im}[/latex]: la partie systématique de l’utilité, c’est-à-dire qu’on peut expliquer.
[latex]\epsilon _{im}[/latex]: un terme d’erreur qui représente les caractéristiques non observables du répondant et de ces alternatives qui vont influencer son choix (par exemple, son niveau de conscience écologique ou son goût pour la conduite automobile).
Pour la partie systématique, on suppose que :
[latex]V_{im}= V(z_{im},s_i; \beta )[/latex]
avec :
[latex]z_{im}[/latex]: des variables d’attribut qui caractérisent le mode m pour le répondant i, par exemple, le temps de déplacement, le coût du mode, son niveau de confort.
[latex]s_i[/latex]: les variables qui caractérisent le répondant i et qui affectent son utilité pour les différents modes, comme l’âge, le sexe ou le niveau de revenu.
[latex]\beta[/latex]: représente les paramètres qu’on vise à estimer.
Les fonctions [latex]U_{im}[/latex] et [latex]V_{im}[/latex] sont des fonctions d’utilité indirectes conditionnelles à un choix de mode. Ainsi, [latex]U_{i1}[/latex] représente le niveau d’utilité que le répondant i peut atteindre conditionnellement à ce qu’il prenne l’automobile. De plus, il s’agit de fonctions d’utilité indirecte obtenues après un processus d’optimisation sous contrainte budgétaire, de sorte qu’elles dépendent des prix et du revenu plutôt que des quantités.
On suppose que les décideurs sont rationnels, de sorte que i va choisir le mode qui lui permet d’atteindre le niveau d’utilité conditionnelle le plus élevé. Par exemple, il choisira l’automobile si [latex]U_{i1} > U_{i2} \text{ et } U_{i1} > U_{i3}[/latex]. Cependant, comme on n’observe pas [latex]U_{im}[/latex] ( [latex]\epsilon_{im}[/latex] n’est pas observable), le choix doit s’analyser en termes de probabilités. Ainsi, la probabilité que i choisissent l’automobile est donnée par :
[latex]P_{i1} = \Pr[U_{i1} > U_{i2} \text{ et } U_{i1} > U_{i3}][/latex]
Si l’on suppose que [latex]\epsilon _{im}[/latex] est identiquement et indépendamment distribué suivant une distribution de Gumbel, on obtient un modèle logit multinomial, de sorte que la probabilité prend la forme explicite suivante [5] :
[latex]P_{i1} = \frac{e^{V_{i1}}}{e^{V_{i1}} + e^{V_{i2}} + e^{V_{i3}}}[/latex]
Souvent la partie systématique de l’utilité est une fonction linéaire des paramètres et des variables, soit :
[latex]V_{im} = \beta_0 + \beta_c c_{im} + \beta_t t_{im} + \beta_z z_{im} + \beta_s s_i[/latex]
avec :
[latex]c_{im}[/latex]: le coût monétaire d’un déplacement avec le mode m pour le répondant i.
[latex]t_{im}[/latex]: le temps de déplacement avec le mode m pour le répondant i.
[latex]z_{im}[/latex]: d’autres variables d’attributs.
[latex]s_{i}[/latex]: les variables de contrôle des caractéristiques de l’individu i.
Avec les données appropriées, il est possible d’estimer les paramètres . À partir de ces estimations, le consentement maximum à payer à la marge pour réduire le temps de déplacement en maintenant le niveau d’utilité constant, soit la VT, est donnée par :
[latex]\left. \frac{\Delta c}{\Delta t} \right|_{\Delta V=0} = -\frac{\beta_t}{\beta_c} = V_T[/latex]
Au moyen de spécifications plus complexes, la VT peut varier entre les individus, en fonction de leurs caractéristiques socioéconomiques ou même entre les modes.
Bibliographie
Abrantes, P. A. et Wardman, M. R. (2011). Meta-analysis of UK values of travel time: An update. Transportation Research Part A: Policy and Practice, 45(1), 1-17.
https://doi.org/10.1016/j.tra.2010.08.003
Barla, P., Lapierre, N., Daziano, R. A. et Herrmann, M. (2015). Reducing automobile dependency on campus using transport demand management: A case study for Quebec City. Canadian Public Policy 41(1), 86-96. 10.3138/cpp.2013-018
Baumstark, L., Bonnet, J., Croq, A., Ducos, G., Meunier, D., Rigard-Cerison, A. et Roquigny, Q. (2013). L’évaluation socioéconomique des investissements publics. Commissariat général à la stratégie et à la prospective https://www.strategie.gouv.fr/
sites/strategie.gouv.fr/files/archives/CGSP_Evaluation_socioeconomique_17092013.pdf
Becker, G. S. (1965). A Theory of the Allocation of Time. The Economic Journal, 75(299), 493-517. https://www.jstor.org/stable/pdf/2228949.pdf
Boardman, A. E., Greenberg, D. H., Vining, A. R. et Weiner, D. L. (2018). Cost-benefit analysis: Concepts and practice (5e éd.). Cambridge University Press.
Bosworth, R. C., Hunter, A. et Kibria, A. (2017). The value of a statistical life: economics and politics. STRATA: Logan, UT, USA.
Chestnut, L. G., Rowe, R. D. et Breffle, W. S. (2012). Economic Valuation of Mortality‐Risk Reduction: Stated Preference Estimates from the United States and Canada. Contemporary Economic Policy, 30(3), 399-416. https://doi.org/10.1111/j.1465-7287.2011.00269.x
Colmer, J. (2020). What is the meaning of (statistical) life? Benefit–cost analysis in the time of COVID-19. Oxford Review of Economic Policy, 36(Issue Supplement 1), S56–S63. https://doi.org/10.1093/oxrep/graa022
Doucouliagos, C., Stanley, T.D. et Giles, M. (2012). Are estimates of the value of a statistical life exaggerated? Journal of Health Economics, 31(1), 197-206.
https://doi.org/10.1016/j.jhealeco.2011.10.001
Environnement et changement climatique Canada (2023). Estimation du coût social des gaz à effet de serre – Orientation provisoire actualisée pour le gouvernement du Canada. https://www.canada.ca/fr/environnement-changement-climatique/services/changements-climatiques/recherche-donnees/cout-social-ges.html
Garbacz, D. (1989). Smoke detector effectiveness and the value of saving a life. Economics Letters, 31(3), 281–286. https://doi.org/10.1016/0165-1765(89)90015-3
Gayer, T., Hamilton, J.T. et Viscusi, W.K. (2000). Private Values of Risk Tradeoffs at Superfund Sites: Housing Market Evidence on Learning about Risk. Review of Economics and Statistics, 82(3), 439-451. https://doi.org/10.1162/003465300558939
ITF. (2019). What is the Value of Saving Travel Time? (Roundtable no 176). OECD Publishing. https://doi.org/10.1787/25198785
Jenkins, R. R., Owens, N. et Wiggins, L. B. (2001). Valuing reduced risks to children: the case of bicycle safety helmets. Contemporary Economic Policy, 19(4), 397-408.
https://doi.org/10.1093/cep/19.4.397
Kniesner, T. J., Viscusi, W. K., Woock, C. et Ziliak, J. P. (2012). The value of a statistical life: Evidence from panel data. Review of Economics and Statistics, 94(1), 74-87.
https://doi.org/10.1162/REST_a_00229
Maguire, K. B., Owens, N. et Simon, N. B. (2004). The Price Premium for Organic Babyfood: A Hedonic Analysis. Journal of Agricultural and Resource Economics, 29(1), 132-149.
Metcalf, G. E., et Stock, J. H. (2017). Integrated assessment models and the social cost of carbon: a review and assessment of US experience. Review of Environmental Economics and Policy, 11(1), 80-99.
McFadden, D. (1974). The measurement of urban travel demand. Journal of Public Economics, 3(4), 303-328. https://doi.org/10.1016/0047-2727(74)90003-6
OECD (2012). Mortality risk valuation in environment, health and transport policies. OECD Publishing. https://doi.org/10.1787/9789264130807-en
Pindyck, R. S. (2013). Climate change policy: what do the models tell us? Journal of Economic Literature, 51(3), 860-872. http://dx.doi.org/10.1257/jel.51.3.860
Rojas, F., López-Castro, M. A. et Júnior, R. P. (2023). Guide de l’analyse avantages-coûts des projets publics en transport routier, Partie 2 : Paramètres (valeurs de 2019). Ministère des Transports et de la Mobilité durable. https://www.transports.gouv.qc.ca/
fr/entreprises-partenaires/entreprises-reseaux-routier/guides-formulaires/
documents-gestionprojetsroutiers/guide-avantages-couts-projets-publics.pdf
Thaler, R. et Rosen, S. (1975). The Value of Saving a Life: Evidence from the Labor Market. Dans N. E. Terleckyj (Éd.), Household Production and Consumption, (p. 265–301). Columbia University Press. https://www.nber.org/system/files/chapters/
c3964/c3964.pdf
Thunström, L., Newbold, S. C., Finnoff, D., Ashworth, M. et Shogren, J. F. (2020). The Benefits and Costs of Using Social Distancing to Flatten the Curve for COVID-19. Journal of Benefit-Cost Analysis, 11(2), 179–195. https://doi.org/10.1017/bca.2020.12
Robinson, L. A., Hammitt, J. K., Aldy, J. E., Krupnick, A. et Baxter, J. (2010). Valuing the risk of death from terrorist attacks. Journal of Homeland Security and Emergency Management, 7(1), 1-25. https://doi.org/10.2202/1547-7355.1626
Rohlfs, C., Sullivan, R. et Kniesner, T. (2015). New estimates of the value of a statistical life using air bag regulations as a quasi-experiment. American Economic Journal: Economic Policy, 7(1), 331-359. http://dx.doi.org/10.1257/pol.20110309
US EPA (2023). Report on the Social Cost of Greenhouse Gases: Estimates Incorporating Recent Scientific Advances. https://www.epa.gov/system/files/
documents/2023-12/epa_scghg_2023_report_final.pdf
Van Benthem, A. (2015). What is the optimal speed limit on freeways? Journal of Public Economics, 124, 44-62. http://dx.doi.org/10.1016/j.jpubeco.2015.02.001
Van den Berg, B., Gafni, A. et Portrait, F. (2017). Attributing a monetary value to patients’ time: A contingent valuation approach. Social Science & Medicine, 179, 182-190. https://doi.org/10.1016/j.socscimed.2017.02.025
Viscusi, W., Hakes, J. et Carlin, A. (1997). Measures of mortality risks. Journal of Risk and Uncertainty, 14, 213-233. https://doi.org/10.1023/A:1007799508646
Wardman, M., Chintakayala, V. P. K. et de Jong, G. (2016). Values of travel time in Europe: Review and meta-analysis. Transportation Research Part A: Policy and Practice, 94, 93-111. https://doi.org/10.1016/j.tra.2016.08.019
Zhang, A., Boardman, A. E., Gillen, D., et Waters, II. W. G. (2004). Towards estimating the social and environmental costs of transportation in Canada : A Report for Transport Canada. Centre for Transportation Studies. http://www.bv.transports.gouv.qc.ca/
mono/0965490.pdf
- Pour le Québec, voir Rojas et al., 2023. ↵
- En effet, étant donné la forme semi-log de l’équation de salaire, on obtient que [latex](\frac{\delta w}{\delta \text{Risque}}) * (\frac{1}{w})=\beta[/latex] de sorte que la prime sur le salaire horaire pour un risque de 1/100 000 est de [latex](\frac{\delta w}{\delta \text{Risque}})=\beta \text w[/latex]. Pour obtenir une valeur annuelle, il faut multiplier par h. Enfin, on multiple par 100 000, l’inverse du changement de risque, pour obtenir la valeur de la vie humaine. ↵
- Environnement Canada établit le CSC entre 2020 à 2080 et celui de deux autres gaz à effet de serre, soit le méthane et l’oxyde nitreux. ↵
- En 2023, le prix sur le marché du carbone est d’environ 50 $ la tonne. ↵
- Si l’on suppose des distributions normales à la place, on obtient le modèle probit multinomial. ↵
L’impact d’un projet se manifestant au-delà des cadres des marchés structurés, tel que les bénéfices environnementaux ou l’amélioration de la qualité de la vie contrastant avec les effets marchands mesurables. Cette distinction, bien qu’importante, peut parfois s’avérer ambiguë.
Montant maximum que les bénéficiaires d’un projet sont prêts à débourser pour en profiter, ou que les victimes d’une nuisance consentent à payer pour l’éviter. Dans certaines situations, le CAP peut s’observer sur les marchés par les comportements d’achat. En revanche, dans d’autres situations où il n’existe pas de marché, il est nécessaire de recourir à des techniques particulières pour l’évaluer.
Méthode consistant à demander directement à un échantillon représentatif de la population concernée d’évaluer leur consentement à payer maximal (CAP) ou le consentement à recevoir minimal (CAR) pour un changement dans un bien non marchand.
Montant minimum que les bénéficiaires d’un impact doivent recevoir pour qu’ils acceptent de s’en priver ou que les victimes d’une nuisance demandent comme compensation pour l’endurer. Dans certaines situations, le CAR peut s’observer sur les marchés par les comportements d’achat. En revanche, dans d’autres situations où il n’existe pas de marché, il est nécessaire de recourir à des techniques particulières pour l’évaluer.
Hausse générale des prix au fil du temps.
Étude de l’évolution de la valeur actualisée nette lors de changements des paramètres et des prévisions. Il existe trois types d’analyse de sensibilité : par paramètre, par scénario et par simulation de Monte-Carlo.
Durée pendant laquelle les coûts et les avantages d’un projet sont comptabilisés. Il s’agit souvent d’une question complexe à laquelle se mêlent des considérations d’ordres technique et pragmatique. Généralement, adopter un horizon court assure une meilleure fiabilité des prévisions, mais avec le risque d’ignorer les effets à plus long terme.
Rendement auquel la collectivité renonce en investissant dans un projet.
Coût de production d’une unité supplémentaire.
Méthode consistant à utiliser des valeurs de référence tirées d’études existantes. Le transfert peut s’effectuer directement ou peut nécessiter certains ajustements pour tenir compte des différences de contexte entre le projet à l’étude et celui de l’étude à l’origine du transfert.
Le bien-être social, ou « bien-être collectif », reflète l’efficacité avec laquelle une société parvient à utiliser ses ressources pour accroître le niveau de satisfaction ou d’utilité de ses membres. Il dépend du niveau de bien-être des individus, de l’efficacité économique et l’équité dans la distribution des ressources. Le bien-être social s’étend donc au-delà de la simple accumulation de richesses matérielles, pour englober des aspects plus larges de la vie en société, visant une amélioration globale des conditions de vie et une réduction des inégalités.

