14.1 La méthode des dépenses de mitigation

Cette approche est également appelée « méthodes des dépenses d’évitement, d’atténuation ou de protection ».

14.1.1 Le principe et le champ d’application

Pour contrer un impact intangible indésirable comme le bruit, les victimes investissent dans des mesures d’évitement, d’atténuation ou de protection. Par exemple, les résidents vivant près d’une route bruyante peuvent investir dans des fenêtres à triple vitrage. Ces dépenses de mitigation peuvent être directement ajoutées à l’évaluation monétaire des dommages (voir la section 13.1), puisqu’il s’agit en effet d’un coût réel.

Alternativement, les dépenses de mitigation peuvent aussi servir à déterminer le consentement à payer pour le bien non marchand. L’approche consiste à exploiter le lien de substitution entre l’effet primaire (le changement dans le bien non marchand) et l’effet secondaire (les dépenses sur un bien marchand), comme l’illustre la Figure 14.1. Grâce à un modèle théorique, il est en effet possible de calculer l’effet primaire à partir de l’effet miroir (voir Dickie, 2017).

 

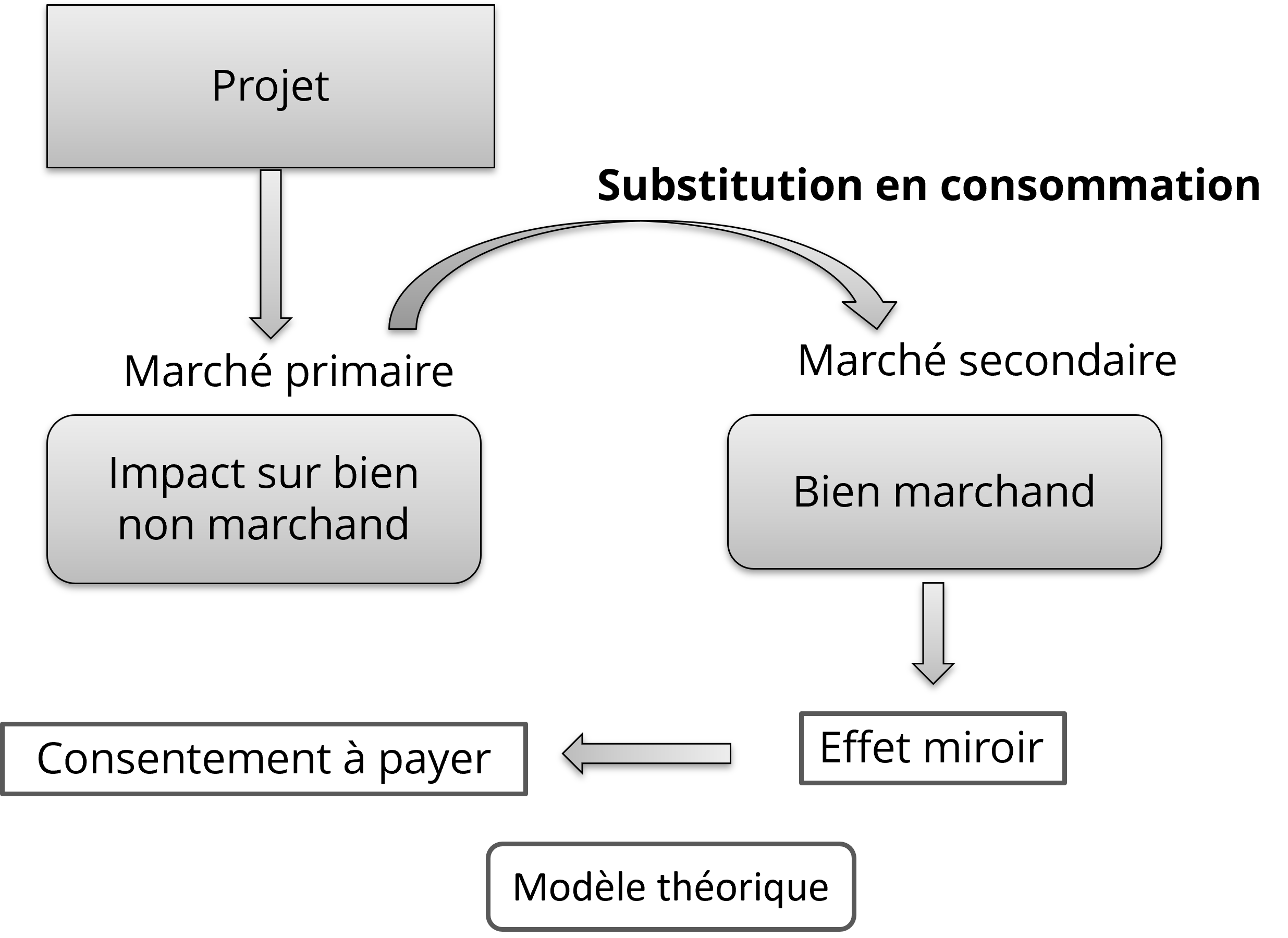
Cette approche repose souvent sur l’idée qu’il existe une « fonction de production » qui détermine le niveau d’une caractéristique procurant directement de l’utilité^[1] à l’individu. Par exemple, un individu valorise sa santé pulmonaire. Le niveau disponible de cette caractéristique est produit par un bien public non marchand et par un bien privé marchand. La santé pulmonaire d’une personne asthmatique dépend positivement de la qualité de l’air et de médicaments pour réduire les crises d’asthme, notamment les bronchodilatateurs. La qualité de l’air et les bronchodilatateurs sont donc des substituts pour « produire » la santé pulmonaire. Plus formellement, le modèle prend la forme suivante :

[latex]U_i(S_i,x_i)[/latex]

U_i est la fonction d’utilité (ou de bien-être) de l’individu i, qui dépend positivement de S_i, le niveau de santé pulmonaire, et de x_i, qui représente de manière générique les autres déterminants. Par ailleurs, S_i est une fonction de la qualité de l’air ambiant (QA), un bien public non marchand, et de la prise d’un médicament (m_i) pour contrôler les crises d’asthme, un bien privé marchand^[2]. On a donc :

[latex]S_i=S(QA,m_i)[/latex]

QA et m_i sont donc des intrants substituts dans la fonction de production de la santé pulmonaire de l’individu. Évidemment, la spécification théorique implique des hypothèses dont la validité doit être justifiée par l’analyste. Dans notre exemple, est-il réaliste de supposer que QA n’a pas d’effet direct sur le niveau d’utilité ?

Un projet industriel qui cause une réduction de QA provoque une augmentation de m_i. Les dépenses d’évitement se mesurent donc par [latex]P_m *\Delta m_i[/latex]_, avec P_m le prix du médicament. Le modèle théorique permet de déterminer le consentement à payer, associé à la dégradation de la qualité de l’air, à partir de l’observation sur les dépenses d’évitement. Il permet aussi de mettre en évidence les hypothèses nécessaires pour faire cette conversion. Dans des cas très particuliers ou en supposant des hypothèses restrictives, l’effet miroir mesurera directement l’effet primaire. Cependant, le plus souvent, le lien est plus complexe.

Pour appliquer cette méthode, il faut qu’il existe des biens marchands substituts au bien non marchand concerné par le projet. Le Tableau 14.1 montre quelques exemples d’applications.

Tableau 14.1 Exemples d’applications de la méthode des dépenses de protection

Effets intangibles	Biens marchands substituts
Pollution qui affecte la santé	Médicaments, soins de santé, purificateurs d’air, masques, réduction des activités à l’extérieur, achat d’équipements sportifs pour l’intérieur
Pollution de l’eau	Systèmes de filtration, achats d’eau en bouteille
Changements climatiques	Climatisation
Valeur de la vie humaine	Dépenses pour réduire les risques : Système de sécurité des véhicules automobiles ; Détecteurs d’incendie ; Mesures de sécurité au travail ; Casques de vélo ; Dépenses pour des crèmes solaires.

14.1.2 Les avantages et les limites

Cette méthode présente l’avantage de s’appuyer sur l’observation de choix réels effectués par des individus. Lorsqu’elle est menée rigoureusement, elle permet d’évaluer le consentement à payer et d’expliquer les hypothèses et les limites de cette estimation. Le développement du modèle théorique et son estimation empirique peuvent cependant être complexes, de sorte qu’en pratique, les études se limitent souvent à valoriser les dépenses d’évitement, sans les convertir de manière rigoureuse en une mesure de l’effet primaire. Cela pose plusieurs problèmes.

1. Les dépenses d’évitement sous-estiment l’effet direct

La quantité demandée de la caractéristique qui est valorisée par l’individu (S_i dans notre exemple) risque de changer à la suite du projet. En effet, le projet industriel dégrade la qualité de l’air, ce qui a pour conséquence d’augmenter le prix implicite pour atteindre un niveau donné de santé pulmonaire S_i. Après le projet, le niveau de S_i risque donc d’être diminué. Cela a pour conséquence que les dépenses d’évitement observées sous-estiment l’impact du projet sur QA. En effet, on voudrait estimer le niveau des dépenses d’évitement tel que S_i reste le même qu’avant le projet.

2. Le bien privé peut générer d’autres avantages

Les dépenses liées à l’installation de fenêtres à triple vitrage pour réduire le bruit du trafic d’une nouvelle autoroute peuvent servir à établir le coût externe du bruit de ce projet. Cependant, ce type de fenêtres permet aussi des économies d’énergie. Dans ce cas, les dépenses de mitigation pourraient surestimer les effets d’un projet qui affecte le niveau du bruit, puisque certaines de ces dépenses peuvent être motivées par des gains énergétiques.

3. Les dépenses d’évitement dépendent du niveau d’information

La réponse dans les marchés aux impacts d’une dégradation d’un aspect intangible dépend du niveau d’information des individus sur les effets nuisibles provoqués par cette dégradation. Si un projet affecte la qualité de l’eau des nappes phréatiques d’une région, mais que ses habitants ne sont pas informés des conséquences, on n’observera pas de dépenses d’évitement, alors que le dommage est pourtant bien réel.

En conclusion, cette méthode permet, soit de compléter l’analyse des impacts monétaires (voir chapitre 13) en ajoutant les dépenses d’évitement, soit de déduire l’effet primaire moyennant le développement d’un cadre théorique rigoureux. Le prochain encadré montre un exemple d’utilisation de cette approche.

14.2 La méthode hédonique

14.2.1 Le principe et le champ d’application

Cette méthode s’appuie sur l’analyse de la valeur de biens hétérogènes ou différenciés comme les maisons ou les voitures. Le principe veut que la valeur du bien dépende de ses caractéristiques, mais également de la quantité et/ou de la qualité des biens non marchands. Par exemple, la valeur d’une maison est tributaire de ses caractéristiques, comme de sa superficie, du nombre de salles de bain et de la présence d’un garage, mais elle découle aussi de la qualité de l’environnement où elle se situe. Une maison se vendra moins cher qu’une autre en tout point identique si elle est localisée dans un quartier plus bruyant. Ainsi, en analysant la décote des propriétés causée par le niveau du bruit extérieur, il est possible d’établir le consentement à payer pour la quiétude. D’autres caractéristiques intangibles peuvent aussi être valorisées, comme la qualité de l’air, la proximité d’un lac ou la nuisance des éoliennes.

La plupart des études hédoniques utilisent les propriétés comme bien différencié, mais certaines prennent aussi la valeur des véhicules automobiles afin d’analyser le consentement à payer pour réduire les risques de mortalité. Certains véhicules sont en effet équipés de dispositifs qui réduisent les risques d’accident, ce qui affecte aussi leur prix de vente.

Plusieurs études hédoniques exploitent également les variations du taux des salaires selon les caractéristiques de l’environnement de travail, comme le niveau de bruit, la qualité de l’air ou les risques de mortalité accidentelle. Dans cette section, nous illustrons la méthode à partir de la valeur des propriétés, mais le chapitre 16 fournit un exemple d’analyse hédonique s’appuyant sur les salaires pour établir la valeur d’une vie humaine.

Une étude hédonique comprend normalement deux étapes. La première étape consiste à estimer économétriquement une fonction hédonique, à partir de laquelle on déduit les prix hédoniques. La deuxième étape vise à estimer la demande pour le bien intangible. Examinons plus en détail ces deux phases en prenant un exemple dans lequel on essaie de mesurer l’avantage brut d’un projet d’amélioration de la qualité de l’air dans une région urbaine à partir de la valeur des propriétés.

Étape 1: L’estimation de la fonction hédonique

Pour réaliser une étude hédonique, il faut disposer de données qui permettent de mesurer statistiquement le lien qui existe entre la valeur marchande et la caractéristique intangible d’intérêt, toutes autres choses étant égales par ailleurs. Dans notre exemple, il faut disposer des données de transaction immobilière, avec les caractéristiques des propriétés et un ou plusieurs indicateurs de la qualité de l’air dans le voisinage. Les données doivent comprendre suffisamment de variabilité au niveau de la qualité de l’air pour pouvoir identifier l’effet spécifique de cette caractéristique sur le prix de vente. Ces données sont utilisées pour estimer statistiquement une fonction hédonique du type suivant :

[latex]VP_i=f(c1_i,c2_i…,cn_i,QA_i,Z_i)[/latex]

avec VP_i la valeur marchande de la propriété i, c1_i,c2_i…,cn_i ses caractéristiques (par exemple, la taille de la résidence, la superficie du terrain, le nombre de salles de bain ou la présence d’une piscine), QA_i une mesure de la qualité de l’air dans le voisinage et Z_i, d’autres variables de contrôle. L’estimation économétrique de cette relation permet d’établir l’impact de la qualité de l’air (QA) sur la valeur marchande des propriétés (VP), alors que toutes les autres caractéristiques demeurent identiques.

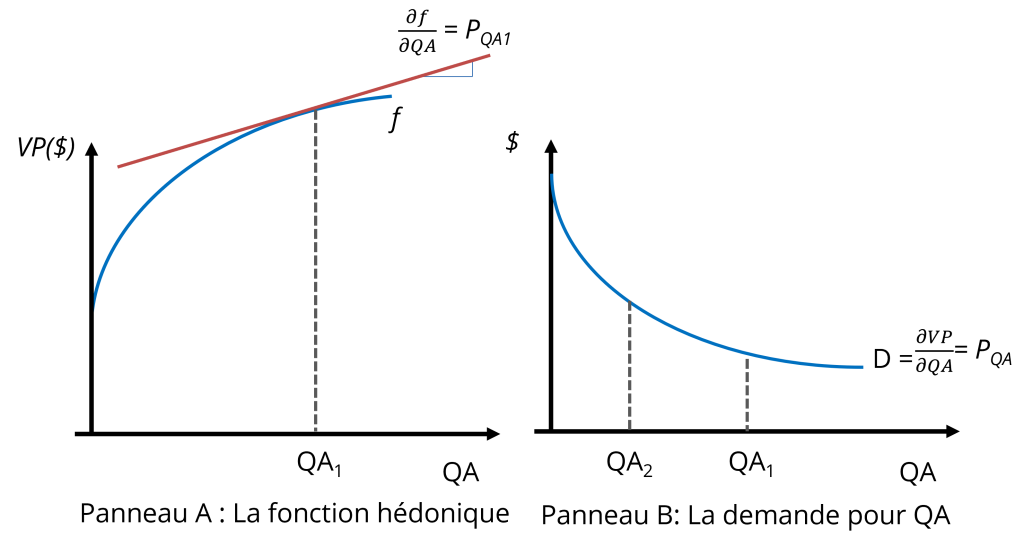
La théorie économique prédit qu’une amélioration de la qualité de l’air augmente la valeur d’une propriété, mais que cet impact diminue au fur et à mesure que QA augmente, à cause d’un effet de satiété. Cela signifie donc que la forme fonctionnelle de la fonction VP estimée doit être concave, comme dans la Figure 14.2, dans le panneau de gauche.

Les résultats de l’étape 1 permettent déjà d’évaluer l’impact de certains projets, comme l’illustre l’encadré sur l’ACA de la décontamination de sites industriels en Nouvelle-Écosse.

Étape 2 : La dérivation de la demande pour QA

À partir des résultats de l’estimation de la fonction hédonique, les prix hédoniques (P_QA dans notre exemple) s’obtiennent en prenant la dérivée partielle de VP par rapport à QA, de sorte que [latex]P_{QA}=\frac{\delta VP}{\delta QA}[/latex].

Graphiquement, P_QA correspond à la pente de la tangente de la fonction VP. Ces prix mesurent le consentement marginal à payer pour QA en fonction de la valeur de QA, ce qui correspond à des observations de la courbe de la demande pour QA. Le panneau B de la Figure 14.2 illustre la demande ainsi obtenue à partir de la fonction hédonique. Le coût d’un projet qui dégrade la qualité de l’air de QA₁ à QA₂ se mesure par l’aire de la surface sous la courbe D, entre QA₁ et QA₂.

Précisons que cette surface mesure une valeur actualisée (ou « capitalisée », dans le langage de l’immobilier), c’est-à-dire qu’elle mesure la valeur actualisée du consentement à payer annuel pour éviter cette dégradation. La capitalisation s’appuie sur un taux d’actualisation qui reflète les préférences intertemporelles des acheteurs, ce qui ne correspond pas nécessairement au taux d’actualisation social.

Pour que les prix hédoniques ainsi obtenus mesurent le consentement marginal à payer pour QA, certaines conditions doivent être vérifiées. Il faut notamment que :

• Le marché immobilier soit concurrentiel et se trouve en équilibre à long terme avec un grand nombre d’acheteurs et de vendeurs ;
• Les coûts de transaction soient faibles ;
• Le marché ne soit pas affecté par d’autres distorsions importantes comme des contraintes sur les prix.
• Les acheteurs disposent réellement de la possibilité d’effectuer un choix entre le prix des résidences et la qualité de l’air.
• L’information sur QA doit être connue des acheteurs.

Par ailleurs, en pratique, il faut aussi tenir compte de l’hétérogénéité des propriétaires. Par exemple, il est probable que le consentement à payer pour QA dépende du niveau de revenu. Cela complique l’estimation de D, puisqu’il faut alors tenir compte des caractéristiques socioéconomiques des acheteurs. Par ailleurs, la demande pour QA peut également dépendre du prix hédonique d’autres caractéristiques qui sont des substituts ou des compléments à QA. Ainsi, la deuxième étape consiste à spécifier et à estimer statistiquement un modèle pour la demande QA.

14.2.2 Les avantages et les limites

Cette approche a l’avantage de reposer sur des bases théoriques précises et de fournir, si les hypothèses nécessaires sont respectées, une évaluation du consentement à payer pour un bien non marchand à partir de choix réels.

Cependant, elle souffre aussi de plusieurs limitations :

1. L’accès aux données pour réaliser une étude hédonique peut être difficile. Par exemple, les données des transactions immobilières sont souvent très coûteuses à obtenir. L’échantillon doit avoir une taille suffisante et comprendre un large éventail de caractéristiques, afin d’éviter des biais causés par des variables manquantes ;
2. Comme nous l’avons mentionné précédemment, le marché du bien marchand utilisé doit être actif et exempt de distorsions significatives, ce qui peut limiter le champ d’application. Par exemple, il n’est pas recommandé d’effectuer une analyse hédonique du prix des maisons dans une région rurale où l’on trouve peu de transactions immobilières ou dans une région où les prix de l’immobilier sont fortement régulés ;
3. Ce type d’analyse est sujet à des difficultés d’ordre statistique, comme des problèmes de biais de sélection, de multi‑colinéarité, d’hétéroscédasticité ou de corrélation des termes d’erreurs ;
4. Il faut également rappeler que l’impact sur la valeur d’un bien durable, comme une maison ou une voiture, est en fait une actualisation (ou une capitalisation) des impacts annuels. L’actualisation se fait sur la base d’un taux d’actualisation privé qui n’est pas observé et qui ne correspond pas nécessairement au taux social.

14.3 La méthode des coûts de transport

14.3.1 Le principe et le champ d’application

Cette méthode est principalement utilisée pour établir les avantages engendrés par des sites récréatifs comme un parc naturel, une plage, un musée ou un paysage. Elle peut aussi servir à évaluer la valeur de caractéristiques non marchandes d’un site, par exemple, la valeur associée au fait que l’eau d’un lac soit d’une qualité qui permette la baignade.

Cette technique exploite un lien de complémentarité entre un bien non marchand gratuit ou pour lequel le prix n’a pas été établi selon les règles du marché, avec pour conséquence qu’il ne varie pas assez dans le temps pour permettre d’identifier la demande. Par exemple, les tarifs d’un musée varient très peu dans le temps ou s’ajustent uniquement à l’inflation.

Plus spécifiquement, cette technique exploite le fait que pour bénéficier du site récréatif, les usagers doivent aussi supporter un coût de déplacement qui varie en fonction du lieu de provenance du visiteur. Cette source de variabilité est ainsi exploitée pour déduire la réaction de la demande du site à un changement du prix généralisé ou pour mesurer comment la demande du site dépend de ses caractéristiques intangibles.

Sur le plan méthodologique, deux approches sont possibles :

1. Les modèles avec un site unique ;
2. Les modèles à utilité aléatoire.

Les modèles à site unique estiment directement la demande pour un site, en particulier sur base des coûts d’accès et du nombre de visites effectuées. Les modèles à utilité aléatoire visent à expliquer le choix d’un site parmi un ensemble de sites possibles. Chaque approche comporte de nombreuses variantes qu’il n’est pas possible de détailler dans ce chapitre (voir Parsons, 2017, pour plus de détails). Dans cette section, nous présentons le principe général de la méthode des coûts de transport au moyen d’un exemple fictif et d’une modélisation simple avec un site unique.

Exemple : la valeur d’une plage

Afin d’évaluer la valeur d’une plage fictive, une enquête a été réalisée auprès de ses visiteurs pour déterminer leur provenance, leurs caractéristiques sociodémographiques et la fréquence annuelle de visite de cette plage. Par ailleurs, on sait que 40550 visiteurs ont payé leur droit d’entrée de 4$/jour durant l’année de référence. Pour simplifier, nous supposons que tous les visiteurs ont utilisé l’automobile pour se rendre à cette plage. Le Tableau 14.2 montre les réponses de quelques répondants.

Tableau 14.2 Quelques observations à partir de la base de données de la fréquentation de la plage

Répondant	Provenance	Fréquence	Classe de revenus	Âge	Situation familiale	Nombres d’accompagnants
1	Ville A	3	50-75	45	Couple	2
2	Ville B	1	> 100	57	Couple	1
3	Ville B	2	75-100	34	Famille	3
4	Ville C	5	75-100	65	Couple	2
5	Ville D	7	< 50	25	Seul	0

Dans notre exemple, la provenance correspond à la ville d’origine, mais en pratique, la provenance pourrait être déterminée plus précisément par le code postal ou par l’adresse exacte du domicile. Par ailleurs, d’autres variables sociodémographiques pourraient être incluses, comme le niveau d’éducation, le type d’activités pratiquées à la plage, les autres plages visitées durant l’année, etc.

À partir de l’information sur la localisation, il est possible de calculer pour chaque répondant le prix généralisé d’une visite, qui dépend du temps de déplacement (aller-retour), de la valeur du temps (qui dépend du revenu du répondant), des coûts d’utilisation de l’automobile, du prix d’entrée et éventuellement du coût du stationnement. Le calcul du prix généralisé doit aussi tenir compte du nombre d’accompagnants, par exemple, en divisant le coût total d’une visite par le nombre de personnes.

On obtient ainsi un nuage de points dans lequel chaque point correspond à un répondant et mesure sur l’axe horizontal le nombre de visites par année et sur l’axe vertical le prix généralisé, comme l’illustre la Figure 14.3.

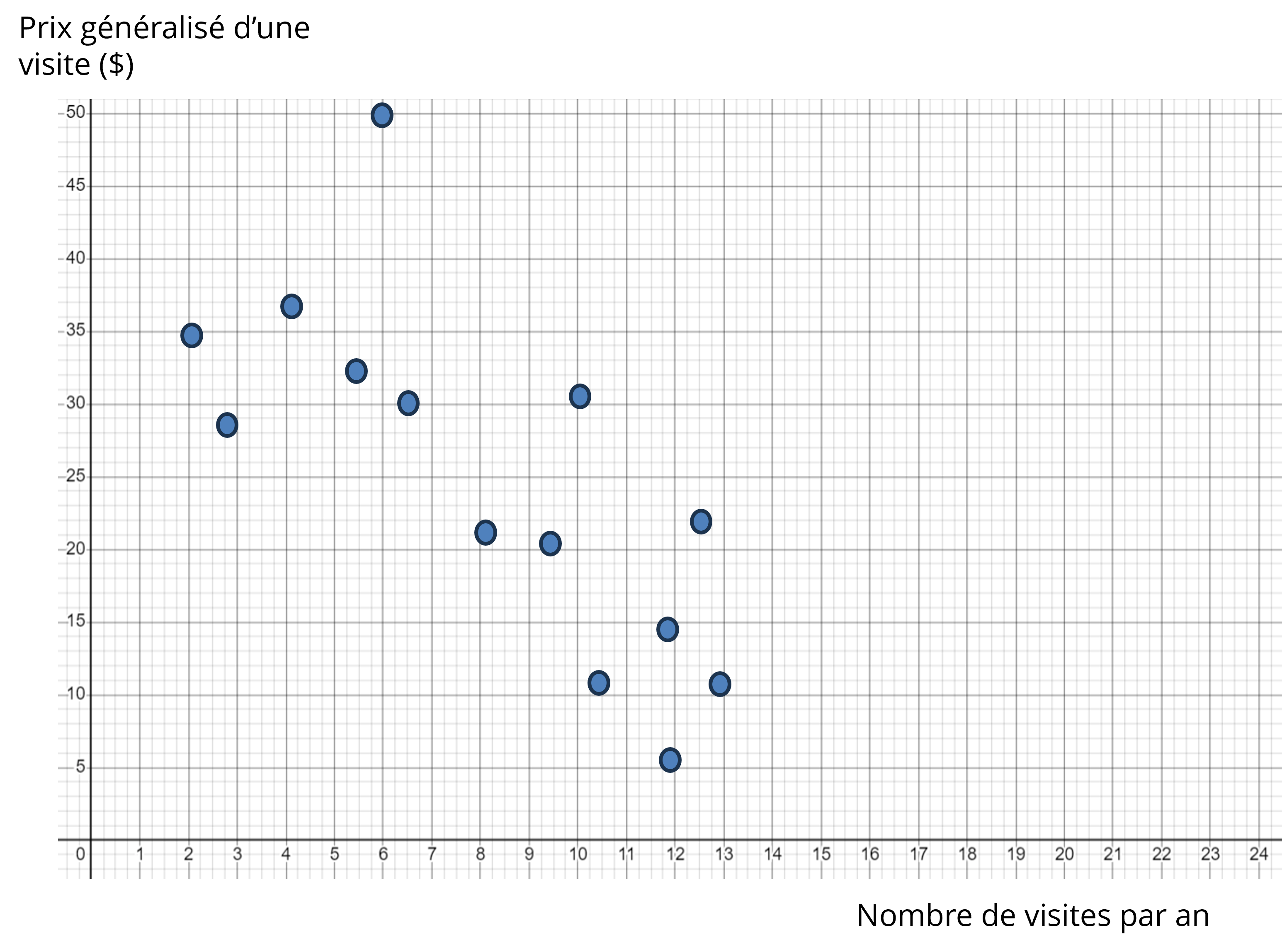
À partir des données, il est possible d’estimer statistiquement la fonction de la demande suivante :

[latex]\text{Visite}_i=f\left(\text{Prix}_i,\text{PS}_i,\text{SD}_i\right)[/latex]

Avec

Visite_i : le nombre de visites annuelles à la plage pour le répondant i ;

Prix_i : le prix généralisé d’une visite à la plage ;

PS_i: les prix généralisés vers des plages substituts pour le répondant i. À partir de l’information sur le lieu de résidence du répondant, il est en effet possible de déterminer le prix généralisé pour d’autres plages accessibles. Cela correspond à prendre en compte le prix des biens substituts ;

SD_i : les caractéristiques sociodémographiques du répondant i qui déterminent ses préférences (par exemple, le revenu, la structure familiale, le type d’activités à la plage, l’âge, etc.).

Une forme fonctionnelle simple souvent estimée est la forme log-linéaire :

[latex]\ln⁡ \left( \text{Visite}_i \right) = \alpha \text{Prix}_i + \beta \text{PS}_i + \gamma \text{SD}_i[/latex]

L’analyse statistique (par exemple, la méthode des moindres carrés) permet d’obtenir une valeur estimée pour des paramètres [latex]\alpha[/latex], [latex]\beta[/latex] et [latex]\gamma[/latex]. Cette procédure permet de déterminer la courbe de la demande du répondant i, en remplaçant SD_i et PS_i par leur valeur. Par exemple, on obtient :

[latex]\ln \left( \text{Visite}_i \right) = -0,01 \text{Prix}_i + 1,5[/latex]

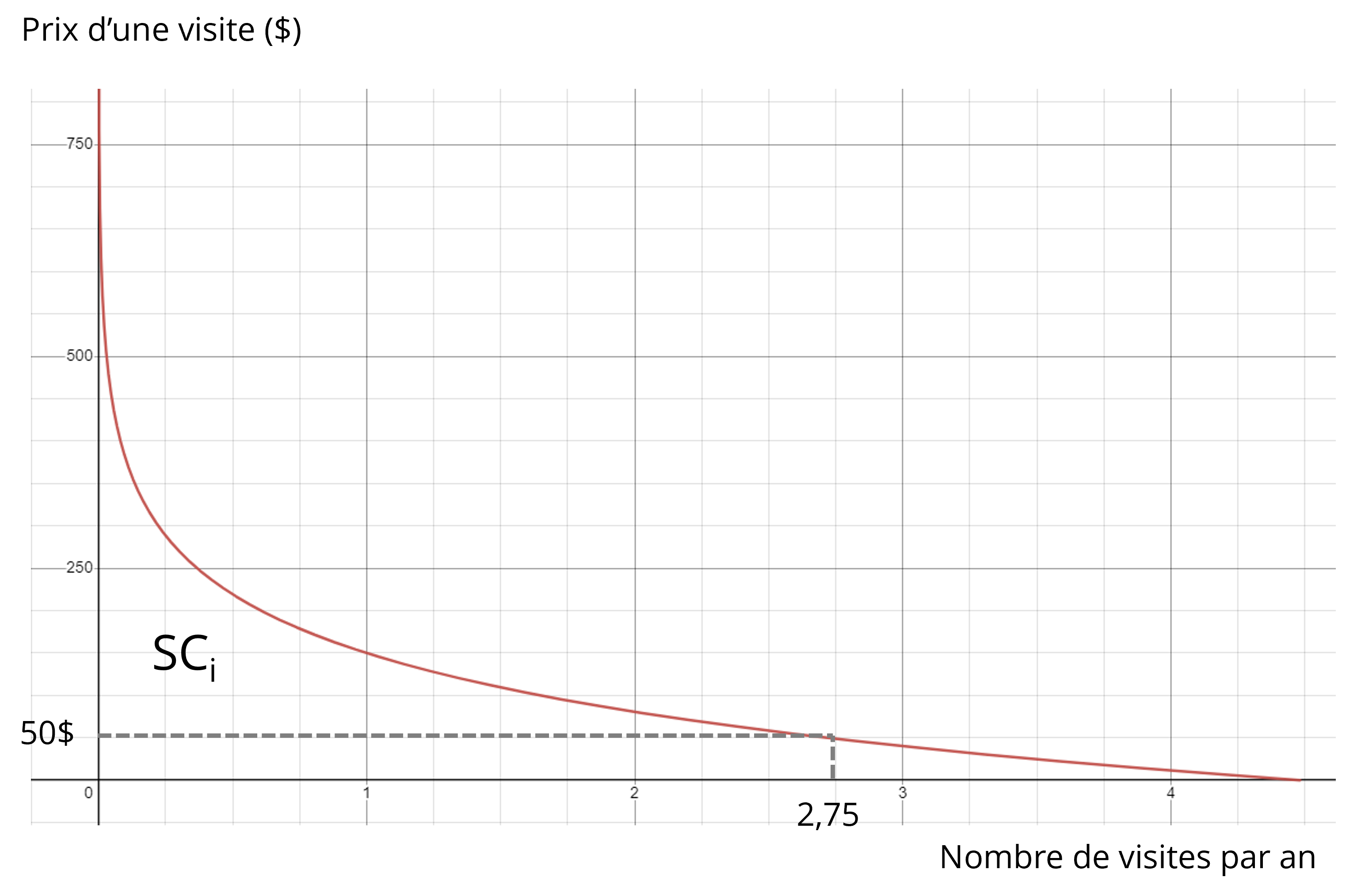
En inversant cette fonction, on obtient la fonction inverse de la demande, qui qualifie le prix comme une fonction de la quantité. La Figure 14.4 illustre cet exemple. Supposons que le prix généralisé pour le répondant i soit de 50$ par visite, le modèle prévoit 2,75 visites par année. Le surplus du consommateur pour ce répondant correspond à l’aire de la surface SC_i. Avec une demande log-linéaire, le surplus du consommateur correspond à [latex]\text{Visite}_i/\left(-\alpha\right)[/latex], soit 2,75/0,01 ou 275$ dans notre exemple. Il est ainsi possible de calculer le surplus pour chacun des répondants, puis d’extrapoler le surplus total pour l’ensemble des visiteurs, en supposant que l’échantillon soit représentatif.

 

14.3.2 Les avantages et les limitations

De nombreux sites touristiques ou récréatifs récoltent des données sur la provenance géographique de leurs visiteurs, de sorte que ces données sont généralement disponibles. Par ailleurs, cette méthode s’inscrit directement dans le cadre des fondements de la microéconomie.

L’application de cette approche comporte cependant plusieurs défis :

1. Un même déplacement est souvent associé à plusieurs motifs (visite d’amis, visite d’autres sites, travail). Dans le cas des déplacements à plusieurs motifs, la répartition des coûts de déplacement entre les motifs complique énormément l’analyse (voir Paterson, 2017) ;
2. Cette procédure peut souffrir d’un biais de sélection menant à une surestimation des avantages liés à l’usage du site. En effet, il est possible que les personnes qui visitent un site présentent des caractéristiques non observables qui expliquent en partie leur attrait pour le site (par exemple, un attrait particulier pour les plages). Cela signifie donc que l’extrapolation des valeurs à l’ensemble de la population peut s’avérer problématique. Il peut alors être conseillé d’effectuer une enquête non seulement auprès des visiteurs, mais aussi auprès de l’ensemble de la population concernée par le site ;
3. La valeur accordée au temps constitue un paramètre qui peut entraîner un impact important sur les résultats. Or, l’évaluation de la valeur du temps pour un déplacement motivé par le loisir est délicate, puisqu’il est possible que la valeur accordée au temps soit faible, voire négative. En effet, le temps passé sur une route panoramique peut procurer un certain avantage.

14.4 Conclusions

Exercices

(*) 1. Une plage est accessible gratuitement. Une enquête a révélé que les personnes qui habitent à moins de 10 km de la plage la visitent en moyenne 4 fois par année. Leur coût de déplacement pour visiter la plage est évalué à 10 $ par visite par personne. Les personnes qui habitent entre 10 km et 20 km visitent la plage en moyenne 2 fois par année. Leur coût de déplacement est en moyenne de 20 $ par visite par personne. Environ 10 000 personnes demeurent à moins de 10 km et 25 000 habitent quelque part entre 10 et 20 km de la plage. À partir de ces données, déterminez le surplus généré par la plage pour la population qui habite à moins de 10 km. [Utilisez une extrapolation linéaire].

(*) 2. Une étude hédonique a été réalisée pour évaluer l’impact des nuisances créées par la proximité d’éoliennes dans une région. Les résultats de l’estimation économétrique de la fonction hédonique sont les suivants :

log(VP)= a₀ + a₁ logX – 0,03 D[500_1000] – 0,07 D[<500]

avec

VP : la valeur des propriétés,

X : des variables de contrôle,

D[500_1000] : une variable dichotomique égale à un, si la propriété est localisée entre 500 mètres et 1000 mètres d’une éolienne,

D[<500] : une variable dichotomique égale à un, si la propriété est localisée à moins de 500 mètres d’une éolienne.

Les coefficients rapportés ci-dessus sont statistiquement significatifs. L’étude hédonique montre également qu’il n’y a aucun effet statistiquement significatif sur les propriétés situées à plus d’un kilomètre d’une éolienne. Le Tableau 14.3 montre la valeur moyenne des propriétés par zone et le nombre de propriétés concernées. À partir de ces informations, valorisez les nuisances associées à la présence d’éoliennes dans cette région.

Tableau 14.3 Valeur moyenne des propriétés

Zones touchées	Valeur moyenne des propriétés	Nombre de propriétés
500 à 1000 mètres	115 000 $	750
< 500 mètres	95 000 $	69

Bibliographie

Bruneau, J. et Mahoney, C. (2022). Intermediate Microeconomics. University of Saskatchewan Edition, https://openpress.usask.ca/econ211/

Dickie, M. (2017). Averting Behavior Methods. Dans: P. A. Champ, K. J. Boyle et T. C. Brown (Éds.) A Primer on Nonmarket Valuation. (2e éd., p. 293-346). Springer Dordrecht. https://doi.org/10.1007/978-94-007-7104-8_8

Ferrara, I., McComb, S., et Missios, P. (2007). Local willingness-to-pay estimates for the remediation of the Sydney tar ponds in Nova Scotia. Canadian Public Policy, 33(4), 441‑458. https://doi.org/10.3138/cpp.33.4.441

Martin, F. (1994). Determining the size of museum subsidies. Journal of Cultural Economics, 18, 255-270. https://doi.org/10.1007/BF01079759

Nelson, J. P. (2004). Meta-analysis of airport noise and hedonic property values. Journal of Transport Economics and Policy, 38(1), 1-27.

Parsons, G.R. (2017). Travel Cost Models. In: Champ, P., Boyle, K., Brown, T. (eds) A Primer on Nonmarket Valuation. The Economics of Non-Market Goods and Resources, vol 13. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-7104-8_6

Wrenn, D. H., Klaiber, H. A., & Jaenicke, E. C. (2016). Unconventional shale gas development, risk perceptions, and averting behavior: Evidence from bottled water purchases. Journal of the Association of Environmental and Resource Economists, 3(4), 779-817. https://doi.org/10.1086/688487