17 Le taux d’actualisation social
Motivation et objectifs d’apprentissage
Si l’on utilise un taux d’actualisation social de 7 %, la valeur actuelle nette (VAN) d’un projet de tramway est négative, mais elle deviendra positive si l’on se sert d’un taux de 4 %. Comment formuler une recommandation dans ce contexte ?
Le choix du taux d’actualisation social (TAS) peut entraîner des répercussions importantes sur les résultats des ACA. En effet, comme nous l’avons expliqué au chapitre 6, un taux plus élevé signifie qu’on accorde moins d’importance aux impacts futurs d’un projet. Dans le cas de projets tels que celui du tramway, qui génèrent des coûts initiaux importants, mais des flux de revenus réguliers tout au long de leur durée de vie, un taux d’actualisation plus élevé tendra souvent à réduire la VAN.
La détermination du TAS représente donc une question capitale qui fait encore débat. Rappelons que le TAS doit mesurer le coût d’opportunité social des ressources mobilisées dans le projet. Ce chapitre examine les méthodes et les enjeux liés au choix de ce paramètre crucial.
À la fin de ce chapitre, vous serez en mesure de comprendre :
- La méthode de détermination du TAS fondée sur une moyenne pondérée des taux du marché ;
- La méthode qui s’appuie sur l’évaluation des préférences intertemporelles ;
- Les enjeux associés à l’actualisation sur de longues périodes ;
- Les approches et les taux utilisés par différentes juridictions.
17.1 Le taux d’actualisation social comme moyenne pondérée des taux du marché
17.1.1 Le marché des capitaux
Pour comprendre cette approche, il est utile de décrire brièvement le fonctionnement d’un marché des capitaux dans un contexte très simple : celui d’une économie fermée et sans distorsion. Cela implique qu’on ne constate ni entrée ni sortie de capitaux du pays, aucune taxe, aucun risque ni asymétrie de l’information. Dans ce monde idéal, la demande en capitaux reflète les décisions d’investissement des entreprises, tandis que l’offre traduit les décisions d’épargne des particuliers.
La demande de capitaux
À tout moment, il existe un ensemble de projets d’investissement, chacun ayant son propre taux de rendement interne privé, soit ρi pour le projet i. La Figure 17.1 présente l’exemple de trois projets d’investissements classés par ordre décroissant de leur taux de rendement interne. La décision d’entreprendre chaque projet dépend de la comparaison entre le taux d’intérêt sur le marché et le taux de rendement interne. Par exemple, si le taux d’intérêt auquel l’entreprise peut financer un projet s’avère supérieur à 19 %, aucun de ces projets ne sera rentable, et la demande de capitaux sera nulle. Si le taux est égal ou inférieur à 19 %, mais supérieur à 10 %, seul le projet A sera réalisé, et la demande en capitaux sera de 5 millions de dollars. Dans la fourchette se situant entre 8 % et 10 %, les projets A et B seront rentables, ce qui entraînera une demande de 8 millions de dollars. Enfin, pour un taux inférieur ou égal à 8 %, les trois projets seront rentables, et la demande en capitaux augmentera à 18 millions de dollars. La Figure 17.1 illustre la demande de capitaux dans notre exemple. Avec un très grand nombre de projets potentiels, la demande en capitaux peut être représentée par une courbe continue et décroissante, comme le montre la Figure 17.2.

La demande de capitaux reflète l’arbitrage entre le taux de rendement interne des projets d’investissement et le taux d’intérêt sur le marché, c’est-à-dire le coût du financement des projets. Pour un taux d’intérêt donné, le projet d’investissement réalisé à la marge a donc un taux de rendement interne égal au taux d’intérêt.
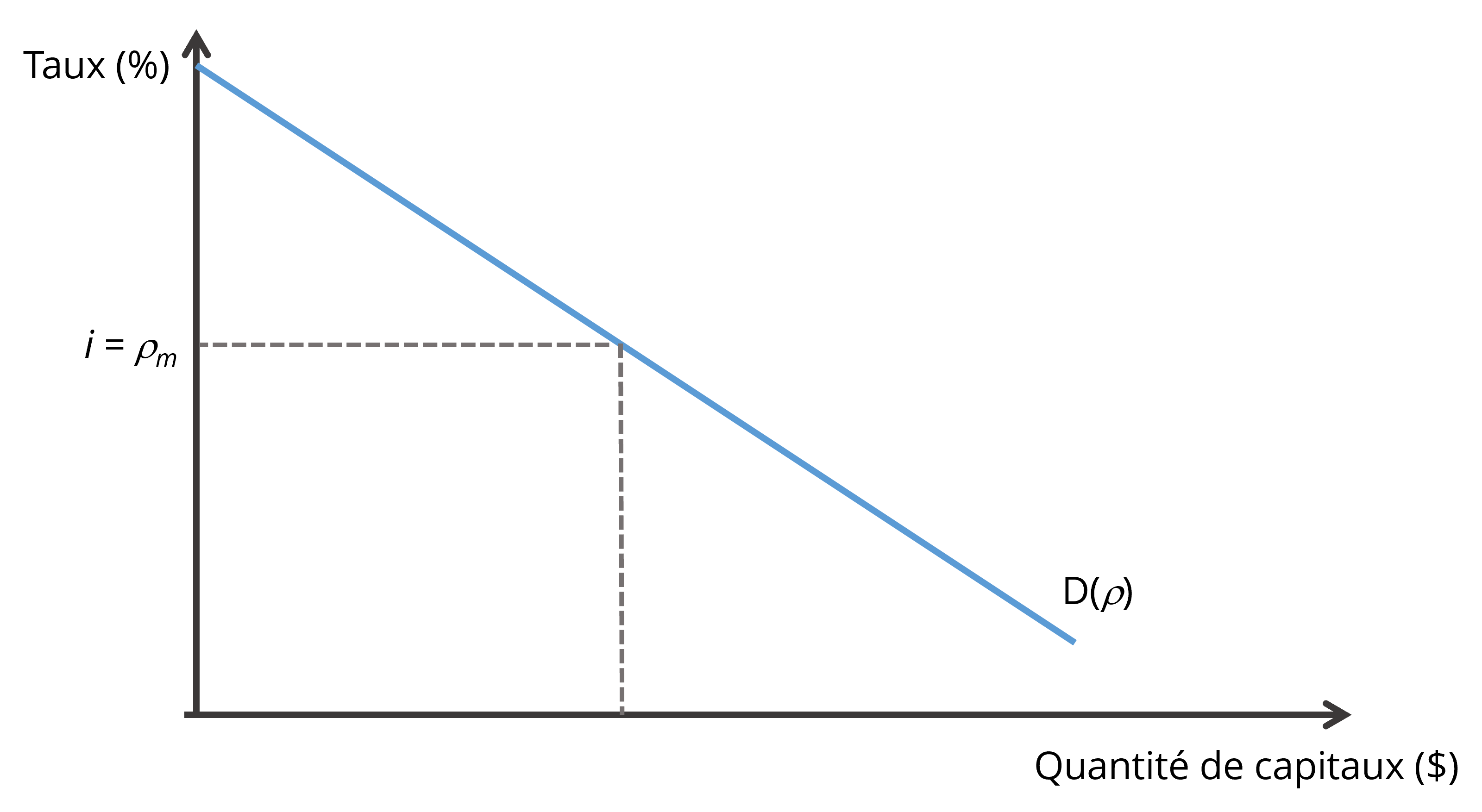
L’offre de capitaux
Dans notre économie simplifiée, l’offre de capitaux provient de l’épargne des individus. Les décisions d’épargne reflètent l’arbitrage entre la consommation actuelle et la consommation future. En effet, l’épargne constitue un moyen de déplacer la consommation dans le temps. Ce compromis dépend du taux de préférence intertemporel.
Le taux de préférence intertemporel, noté par δ, mesure le taux d’intérêt minimum exigé pour renoncer à consommer 1$ aujourd’hui pour pouvoir consommer (1 + δ %) à l’avenir.
Si une personne présente un δ égal à 20 %, cela signifie qu’elle sera prête à consommer moins aujourd’hui si le montant ainsi épargné lui rapporte 20 % d’intérêt. Au niveau individuel, on s’attend à ce que δ augmente au fur et à mesure que le montant déjà épargné s’accroît. L’offre individuelle d’épargne augmente donc avec le taux d’intérêt. Par ailleurs, le taux de préférence intertemporel est variable au sein de la population. Cela entraîne également que la courbe de l’offre de capital augmente avec le taux d’intérêt, puisque plus le taux d’intérêt est élevé, plus de personnes épargneront. La Figure 17.3 illustre la courbe de l’offre de capitaux. Si le taux d’intérêt est de i %, la quantité de capitaux offerts est de Q0, et le taux de préférence intertemporel à la marge est égal à i %. L’épargnant à la marge sera donc indifférent à épargner ou à consommer davantage aujourd’hui.
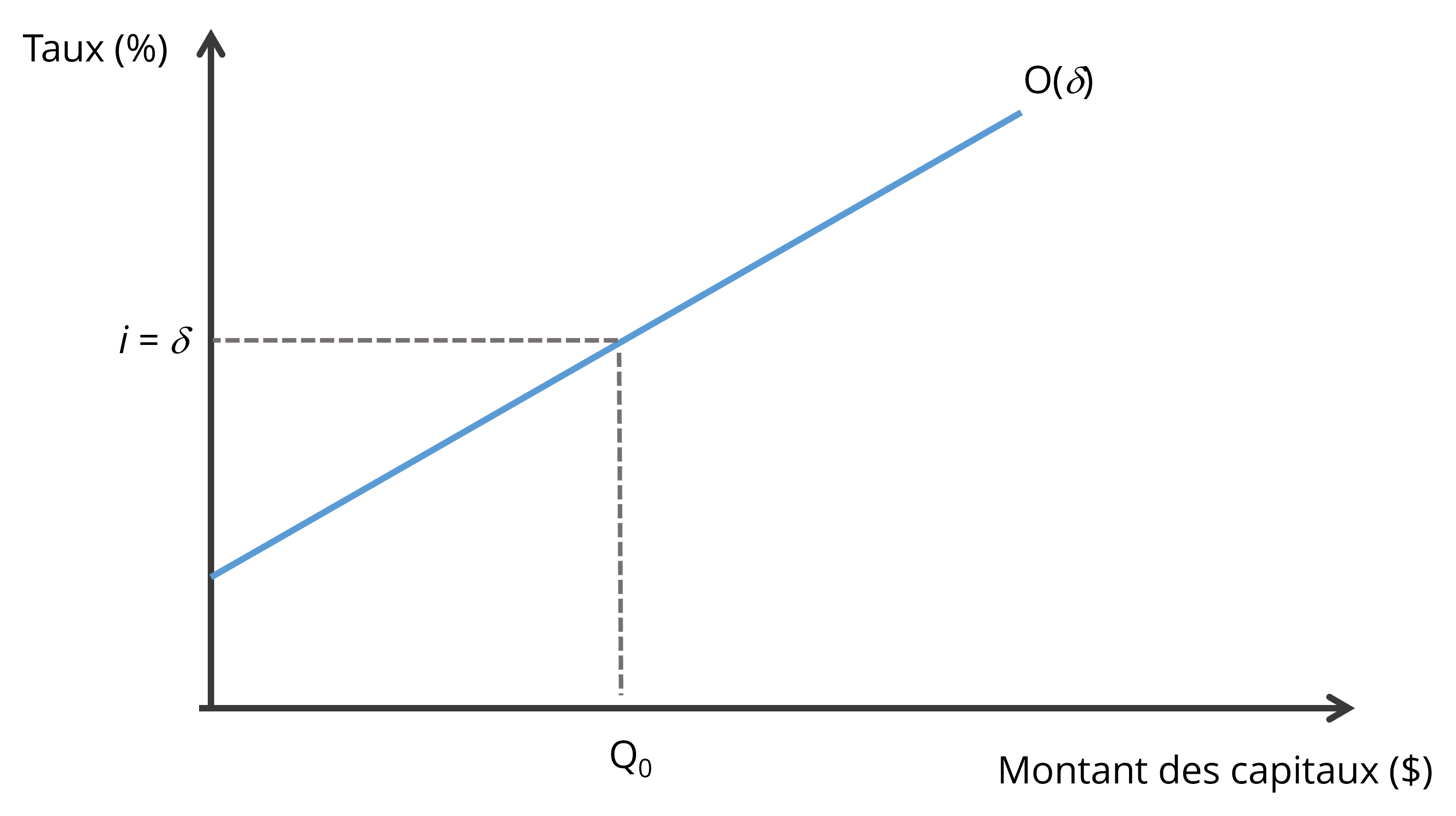
L’équilibre du marché des capitaux
Dans cette situation idéalisée, l’équilibre se produit à l’intersection de l’offre et de la demande, au taux d’intérêt d’équilibre i* (voir la Figure 17.4). Ce taux représente à la fois le coût de renonciation des investissements à la marge et le taux de préférence intertemporel à la marge.
Dans ce contexte, l’ACA d’un projet additionnel dont la taille n’est pas susceptible d’influencer le taux d’intérêt d’équilibre doit être évaluée en utilisant un TAS égal à i*. En effet, peu importe que les fonds investis dans le projet proviennent d’un accroissement de l’épargne ou d’un évincement d’autres projets, le coût de renonciation est i*, puisque i* = ρ = δ.
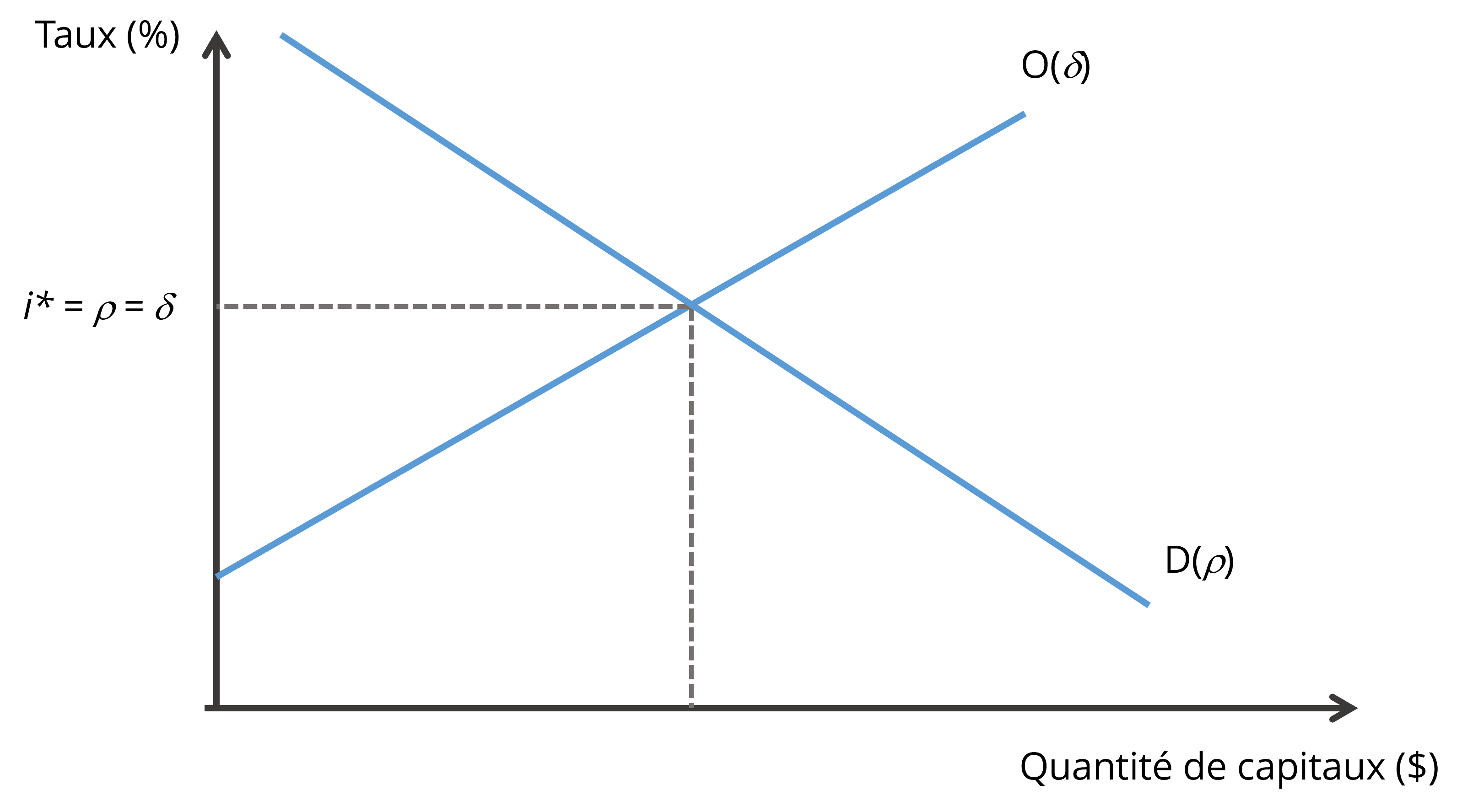
En présence de distorsion
Comme c’est le cas pour d’autres marchés, celui des capitaux est affecté par des distorsions, ce qui fait varier le coût de renonciation des fonds investis dans un projet en fonction de leur provenance. On peut illustrer cela en supposant la présence d’une taxe sur l’épargne de t%. Comme mentionné précédemment, cette taxe engendre une disparité entre le taux payé par les demandeurs de capitaux et celui reçu par les individus qui les fournissent. Dans la Figure 17.5, le taux d’intérêt d’équilibre i* reflète le taux de rendement de l’investissement à la marge, mais il ne représente plus le taux de préférence intertemporel à la marge, puisque δ = i* – t.
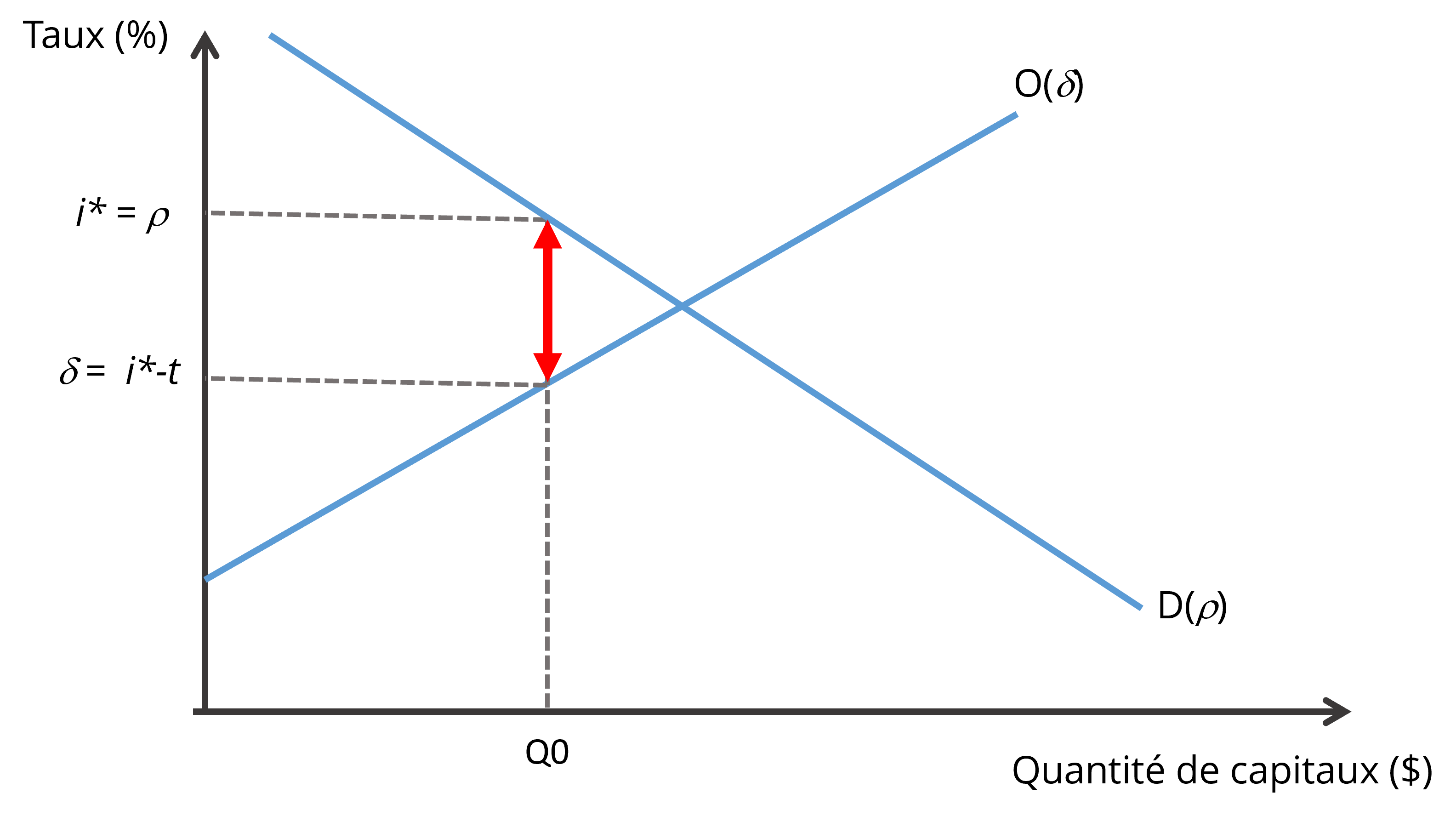
Un nouveau projet (P) entraîne un déplacement de la demande de capitaux vers la droite (voir la Figure 17.6). Une partie des capitaux du projet provient d’un évincement d’autres projets (entre Q’ et Q) et est valorisée au coût de renonciation i*. En revanche, la partie qui résulte d’un accroissement de l’épargne (entre Q0 et Q1) enregistre un coût de renonciation de i* – t. Il s’agit donc ici du même raisonnement que nous avons effectué pour d’autres intrants au chapitre 11.

Cet exemple illustre le fait que la provenance des capitaux d’un projet détermine le taux d’actualisation. Ainsi, Harberger (1969) propose d’évaluer le taux d’actualisation social à partir d’une moyenne pondérée suivant la provenance des fonds, comme nous le décrivons dans la prochaine sous-section.
Le TAS comme moyenne pondérée des taux du marché
Dans une économie ouverte, les fonds pour soutenir un projet peuvent aussi provenir d’emprunts externes. Dans ce contexte, le taux d’actualisation social peut être évalué comme une moyenne pondérée suivant la formule suivante :
TAS% = a ρ%+b δ%+(1-a-bi)%
dans laquelle
TAS % : représente le taux d’actualisation social en pourcentage ;
a : la part des ressources du projet qui provient d’un évincement des investissements privés de l’économie ;
ρ% : le taux du rendement interne à la marge des investissements privés ;
b : la part des ressources du projet provenant d’un évincement de la consommation privée (épargne) ;
δ % : le taux de préférence intertemporelle à la marge ;
i % : le taux d’intérêt sur les emprunts étrangers à la marge.
La mise en application pratique de cette formule exige d’accorder une valeur à chacun de ces paramètres, ce qui pose plusieurs défis :
- Les taux doivent représenter ce qui prévaut à la marge plutôt qu’en moyenne. Par exemple, si un projet gouvernemental évince un investissement privé, il s’agira d’un investissement à la marge dont la rentabilité sera plus faible que la moyenne des investissements. L’utilisation d’un taux de rendement moyen sur les investissements risque donc de surestimer le taux à la marge. En revanche, le taux moyen sur l’épargne sous-évalue le taux de préférence intertemporelle à la marge ;
- Les marchés des capitaux proposent un grand nombre de taux, qui varient notamment en fonction du risque. Chaque projet soumis à une ACA est également caractérisé par un risque spécifique, ce qui pourrait justifier que le taux d’actualisation social comprenne une prime de risque spécifique. Ce n’est cependant pas l’approche généralement recommandée. Il est plutôt proposé d’utiliser un taux d’actualisation social sans prime de risque spécifique, l’argument voulant que les pouvoirs publics disposent d’un large éventail de projets, ce qui permet la diversification des risques spécifiques. En revanche, comme le rappellent Boyer, Gravel et Mokbel (2013), les projets entraînent aussi un risque systémique non diversifiable. Nous reviendrons sur cet aspect à la section 17.2 et au Chapitre 18;
- L’évaluation des poids n’est pas simple, car elle exige de déterminer l’élasticité des différentes sources possibles de capitaux à la suite d’une variation des taux.
Le Tableau 17.1 présente des évaluations du TAS pour le Canada et pour le Québec en se fondant sur cette approche. On constate que le TAS recommandé par le ministère des Transports et de la Mobilité durable (Rojas et al, 2023a et b) pour les ACA des projets publics en transport routier est assez faible, à 2,7 %. Cette évaluation repose sur les taux en vigueur en 2019, une période caractérisée par des niveaux particulièrement bas. Il est généralement conseillé d’opter pour l’utilisation de taux moyens historiques, c’est-à-dire des taux calculés sur la base d’une moyenne sur plusieurs années, afin de garantir une estimation plus représentative et fiable.
| Source | ρ | δ | i | a | b | TAS |
| Canada | ||||||
| Jenkins et Kuo (2007) | 11,5 | 4 | 6 | 0,4616 | 0,1538 | 8,23 |
| Boardman et al., (2010) | 7 | 1,75 | 3,9 | 0,4616 | 0,1538 | 5 |
| Québec | ||||||
| Rojas et al. (2023b)* | 3,25 | 2,25 | – | 0,46 | 0,54 | 2,7 |
| * Le paramètre ρ est calculé à partir d’une moyenne pondérée, intégrant 10 % du taux S&P et 90 % du rendement des obligations sur 20 ans émises par des sociétés canadiennes. Quant à δ, il se base sur la moyenne des taux suivants : les dépôts de 5 ans des particuliers, les certificats de placement garanti (CPG) de 5 ans, ainsi que les obligations de 10 et 20 ans émises par le Québec, en plus de la moyenne de l’indice S&P. Les pondérations appliquées dérivent de la proportion des investissements en capital fixe des entreprises et de l’épargne personnelle par rapport à la somme de ces deux agrégats macroéconomiques, à laquelle s’ajoute le total de la consommation des biens durables et semi-durables. | ||||||
La confusion entre le taux de financement d’un projet et le taux d’actualisation social
 Il est crucial de ne pas confondre le taux auquel les pouvoirs publics peuvent financer un projet et le taux d’actualisation social, comme l’expliquent Boyer, Gravel et Mokbel (2013). Les pouvoirs publics bénéficient généralement de taux de financement avantageux, car ils ne sont pas tenus de verser une prime de risque aux prêteurs. Cependant, cela ne signifie pas que le risque associé à ces projets publics disparaît. En réalité, c’est la population, au moyen des taxes et des impôts, qui supporte le risque et, par conséquent, le coût en cas de problème dans un projet. Ainsi, l’utilisation de taux sur les obligations gouvernementales pour la détermination du TAS est contestable.
Il est crucial de ne pas confondre le taux auquel les pouvoirs publics peuvent financer un projet et le taux d’actualisation social, comme l’expliquent Boyer, Gravel et Mokbel (2013). Les pouvoirs publics bénéficient généralement de taux de financement avantageux, car ils ne sont pas tenus de verser une prime de risque aux prêteurs. Cependant, cela ne signifie pas que le risque associé à ces projets publics disparaît. En réalité, c’est la population, au moyen des taxes et des impôts, qui supporte le risque et, par conséquent, le coût en cas de problème dans un projet. Ainsi, l’utilisation de taux sur les obligations gouvernementales pour la détermination du TAS est contestable.
17.2 Le TAS et le taux de préférence intertemporel social
Une stratégie alternative d’évaluation du TAS se fonde sur le Taux de Préférence Intertemporelle Social (TPIS), qui est le taux implicite choisi par la société pour répartir les ressources entre la consommation actuelle et future. Cette méthode est particulièrement pertinente dans le contexte où le financement des projets gouvernementaux provient principalement des recettes fiscales actuelles ou de l’augmentation de la dette publique, qui nécessitera à terme un remboursement par le biais de taxes futures. Ainsi, selon cette perspective, les projets gouvernementaux tendent à se substituer principalement à la consommation, actuelle ou future, plutôt qu’aux investissements privés.
Le taux de préférence intertemporel social est bien entendu lié au taux δ discuté précédemment. Toutefois, il faut également tenir compte de la croissance attendue du niveau de vie et de l’évolution de l’utilité marginale à consommer. Plus précisément, à partir d’un modèle de croissance néoclassique, Ramsey (1928) a dérivé la formule suivante :
TPIS = δ + g ε
dans laquelle :
TPIS : représente le taux de préférence intemporel social;
δ : le taux de préférence intertemporel, souvent caractérisé de « pur », pour mieux le distinguer du TPIS ;
g : le taux de croissance attendu de la consommation par personne ;
ε : la valeur absolue de l’élasticité de l’utilité marginale de la consommation par rapport à la croissance, soit le pourcentage de réduction de l’utilité marginale de la consommation à la suite de la croissance de 1 % du niveau de la consommation.
L’explication de l’équation connue sous le nom de « formule de Ramsey » repose sur un principe clair : la répartition des ressources entre la consommation présente et future doit considérer l’impatience « pure » des individus ainsi que l’ajustement pour la croissance économique anticipée. Cette dernière affecte l’utilité marginale d’un dollar de consommation future, la rendant inférieure à celle d’un dollar consommé aujourd’hui, si l’on suppose que la croissance économique se maintient. Autrement dit, la formule de Ramsey prend en compte à la fois le désir d’une satisfaction immédiate et les attentes quant à la croissance économique future, qui influencent la valeur attribuée à la consommation future par rapport à la consommation actuelle.
L’analyse de cette formule dans un contexte multigénérationnel est particulièrement éclairante. En effet, la lutte contre les changements climatiques impose des sacrifices à la génération existante pour fournir des avantages (plus précisément, pour éviter des coûts) aux générations futures. L’arbitrage doit donc prendre en compte le fait que les générations futures devraient, si le développement économique se poursuit, devenir plus riches, de sorte que l’utilité marginale future sera plus faible que l’utilité marginale actuelle. En d’autres termes, un dollar sacrifié réduit davantage le bien-être actuelle que l’augmentation du bien-être dans le futur par un dollar supplémentaire.
En s’appuyant sur l‘évolution historique du taux de croissance au Canada, Boardman et al., (2010) proposent d’employer g = 1,7 %, avec une analyse de sensibilité à 1,5 % et 2 %. Pour ε et ρ, ces auteurs effectuent une revue des évaluations existantes et proposent d’utiliser une valeur de 1,5 pour ε, avec une analyse de sensibilité à 1 et à 4, et une valeur de 1 pour ρ. Sur cette base, le TAS au Canada devrait être de 3,5 %, avec une analyse de sensibilité variant entre 1,5 % et 7 %.
En France, l’application de la formule de Ramsey a été étendue pour inclure le risque systémique associé à un projet (Baumstark et al., 2013). Dans cette perspective, le risque systémique d’un projet ne pourrait pas être éliminé par la diversification en raison de sa corrélation avec les tendances globales de l’économie. Par exemple, les avantages nets d’un projet de transport sont souvent positivement corrélés à la croissance économique, ce qui implique un risque de rendement inférieur en cas de détérioration des conditions économiques générales. Un tel risque devrait donc se traduire par une augmentation du TAS. À l’inverse, un projet dont les avantages nets sont susceptibles de s’accroître dans un contexte de ralentissement économique présente un risque spécifique négatif, justifiant ainsi l’adoption d’un TAS réduit. Un exemple est celui de la fréquentation hospitalière, qui tend à s’intensifier en période de récession économique.
Un comité d’experts mandatés par le gouvernement français (Gostner et Ni, 2023) recommande d’ajuster le TAS selon le risque systémique d’un projet en utilisant la formule suivante :
TAS = TAS sans risque + β x Prime de risque systémique
β mesurant la sensibilité des avantages nets futurs du projet par la croissance du PIB par habitant. Le TAS sans risque est déterminé selon la formule de Ramsey.
Pour l’année 2021, le comité recommande les valeurs suivantes :
- Taux sans risque de 1,2 % ;
- Prime de risque de 2 % ;
- β = 1,1 pour des projets en transport urbain ;
- β = 1,2 pour le transport régional ;
- β = 1,7 pour le transport sur une longue distance ;
- β = 1,4 pour le transport ferroviaire de fret ;
- β = 1 pour d’autres projets en attendant les résultats d’études sectorielles complémentaires.
17.3 Le TAS et horizon temporel
Comme mentionné dans le chapitre 6, l’actualisation fait en sorte que la valeur accordée aux avantages futurs décroît de manière géométrique au fil du temps. Cela conduit à ce que, plus ou moins rapidement, les conséquences futures se retrouvent à être considérées comme négligeables. Prenons l’exemple d’un taux d’actualisation social fixé à 3,5 %. Dans ce cas, une somme d’un milliard de dollars perçue dans 50 ans présente une VAN de 179 millions de dollars. Si cette même somme est reçue dans 100 ans, la VAN diminue à 32 millions de dollars, et elle chute à 10 millions de dollars si le paiement s’effectue dans 200 ans.
Cela peut s’avérer problématique lorsqu’on analyse des projets qui comportent des conséquences sur les générations futures, car cela leur accorde très peu de poids. Il existe donc un risque de « dictature du présent ». Un projet qui coûte peu aujourd’hui pour prévenir des dommages importants dans un avenir lointain pourrait ne pas passer le test de l’ACA. Cela représente assez bien l’enjeu de la lutte contre les changements climatiques. Ainsi, certains chercheurs, comme Stern (2007), recommandent d’utiliser un TAS égal à zéro (ou très faible) pour analyser les projets multigénérationnels (dès que T > 50 ans).
Cependant, comme le souligne Nordhaus (2007), l’utilisation d’un TAS très faible peut mener à une « dictature du futur ». En effet, étant donné que les générations futures seront plus nombreuses que la génération actuelle, un projet qui exige des sacrifices énormes aujourd’hui pour engendrer des avantages modestes, mais durables dans le temps pourrait passer le test de l’ACA. Par exemple, un projet qui coûte un milliard de dollars aujourd’hui et qui générera 11 millions de dollars pendant 100 ans serait jugé rentable.
La détermination du TAS pour des projets s’étendant sur un très long horizon demeure un enjeu débattu. Une solution proposée consiste à diminuer le TAS avec le temps. Par exemple, Boardman et al., (2010) proposent la structure de TAS suivante :
[latex]\text{TAS} = \begin{cases} 3.5\% & \text{pour } t = 1 \text{ à } 50 \\ 2.5\% & \text{pour } t = 51 \text{ à } 100 \\ 2\% & \text{pour } t = 101 \text{ à } 200 \\ 1.5\% & \text{pour } t > 200 \end{cases}[/latex]
Cette approche, semblable à l’actualisation hyperbolique, repose sur l’idée que l’importance accordée aux avantages futurs décroît de manière accélérée initialement, pour ensuite ralentir progressivement à mesure que l’on envisage un horizon temporel plus lointain. Cette notion trouve notamment son fondement dans les observations expérimentales qui mettent en lumière cette tendance comportementale chez les individus. Par exemple, des études, comme celle de Green et al. (1994), ont montré que les personnes ont une préférence pour recevoir 5 000 $ immédiatement plutôt que 7 000 $ dans un an. Cependant, ces mêmes personnes opteraient pour 7 000 $ dans six ans au lieu de 5 000 $ dans cinq ans.
L’adoption de cette méthode d’actualisation vise à reconnaître les impacts significatifs, mais éloignés dans le temps, tout en évitant de placer le futur dans une position de suprématie absolue. Néanmoins, l’actualisation hyperbolique peut conduire à des décisions temporellement incohérentes. Dans l’exemple mentionné, au bout de cinq ans, l’individu pourrait regretter sa décision initiale, souhaitant alors avoir opté pour la réception immédiate de 5 000 $ plutôt que d’attendre un an supplémentaire pour obtenir 7 000 $.
17.4 En pratique
Malheureusement, il n’existe pas de consensus sur le choix du TAS, ni même sur la méthodologie pour le déterminer. De plus, on recense encore plusieurs enjeux conceptuels non résolus. Plusieurs organismes et juridictions ont adopté des normes ou des recommandations sur le TAS, comme le montre le Tableau 17.2. Par exemple, la dernière mise à jour du Guide de l’analyse coûts-avantages pour le Canada recommande d’utiliser un taux de base de 7%, sauf pour des projets en matière d’environnement et de santé, pour lesquels le taux peut être réduit à 3%.
Comme mentionné à la section 17.1, le ministère des Transports et de la Mobilité durable du Québec recommande un taux d’actualisation de 2,7%, ce qui est probablement trop bas, puisque ce taux s’appuie sur les valeurs des taux d’une année durant laquelle les taux étaient historiquement bas.
L’Agence de la protection de l’environnement des États-Unis conseille de présenter initialement les coûts et avantages d’un projet sous forme de flux temporels non actualisés. La VAN est ensuite calculée en employant deux types de TAS : l’un reflétant le coût d'opportunité du capital privé, et l’autre basé sur le taux de préférence intertemporelle. Cette méthodologie vise à offrir aux décideurs une analyse plus nuancée de la rentabilité sociale d’un projet. Il est également essentiel de rappeler l’importance de réaliser une analyse de sensibilité sur le TAS pour appréhender l’impact de variations de ce taux sur l’évaluation du projet.
En s’appuyant sur les évaluations disponibles, l’utilisation d’un TAS de 7% avec une analyse complémentaire à 3% semble judicieuse pour des projets générationnels. Pour des projets dont la portée est multigénérationnelle (de plus de 50 ans), une analyse avec un TAS qui diminue avec le temps peut également s’avérer justifiée.
| Juridiction et organisme | TAS réel | Remarque |
| Canada – Guide d’analyse coûts-avantages pour le Canada | 7 % | 3% pour des projets en environnement et en santé. Moyenne pondérée et formule de Ramsey |
| Québec – Rojas et al. (2023b) | 2,7 % | Moyenne pondérée |
| Québec – Tagne Kuelah (2016) | 6% | Recommandation fondée sur Montmarquette et Scott (2007) et Boyer, Gravel et Mokbel(2013) |
| U.S., Environmental Protection Agency (2010) | 3% et 7% | Pour les projets de plus de 50 ans, utiliser 3% et utiliser l’actualisation hyperbolique. |
| U.S., Office of Management and Budget (2018) | 3% et 7% | 3% correspond au rendement moyen des obligations d’État à 10 ans et 7 % au rendement moyen avant impôt du capital privé. |
| France, Gostner et Ni (2023) | 1,2% | Ajout d’une prime pour le risque systémique allant jusqu’à 3 % |
| UK, HM Treasury Green Book (2018) | 3,5% | Pour les projets d’une durée supérieure à 30 ans, le TAS est ajusté à 3 % pour la période couvrant de 31 à 75 ans et réduit à 2,5 % pour celle s’étendant de 76 à 125 ans. |
17.5 Conclusions
Éléments clés à retenir
- Le choix du TAS peut entraîner des conséquences importantes sur l’ACA.
- Malheureusement, il n’existe pas de consensus sur le choix du TAS, et plusieurs enjeux conceptuels sont encore débattus.
- La méthode de la moyenne pondérée prend en compte la source des fonds investis, comme l’évincement des investissements privés, la consommation privée ou les emprunts à l’étranger, pour mesurer le coût d’opportunité social du capital.
- La méthode du taux de préférence intertemporelle sociale s’appuie sur l’analyse du choix de la société entre le présent et l’avenir.
- L’actualisation à très long terme (T > 50 ans) présente des défis en termes d’équité entre les générations, car elle peut sous-représenter les générations futures ou au contraire leur accorder trop de poids. Une solution proposée consiste à utiliser un TAS qui diminue avec le temps, malgré que cette approche soulève des questions de cohérence.
- En pratique, certaines juridictions ont adopté des normes sur le TAS.
- En l’absence de normes, l’actualisation avec un TAS de 3 % et de 7 % semble judicieuse pour les projets de cinquante ans et moins. Pour les projets de plus de cinquante ans, il peut être utile d’actualiser avec un TAS décroissant dans le temps.
- Une ACA devrait aussi présenter les flux d’avantages et de coûts au cours du temps, sans les actualiser, en plus d’effectuer une analyse de sensibilité par rapport au TAS.
Retour sur la motivation
La VAN d’un projet de tramway est négative si l’on utilise un taux d’actualisation sociale de 7 %, mais devient positive si l’on utilise un taux de 4 %. Comment faire une recommandation dans ce contexte ?
Solution
Évidemment, il n’existe pas de réponse précise à cette question. L’analyste doit faire preuve de jugement, tout en étant le plus transparent possible dans ses recommandations. Dans cette situation, l’analyste devra, notamment :
- Vérifier si le commanditaire de l’ACA dispose d’une valeur de référence pour le TAS ;
- Si ce n’est pas le cas, il faudra tenir compte de la durée de vie du projet. Dans le cas d’un tramway, sa durée de vie est généralement inférieure à 50 ans, ce qui signifie qu’il ne s’agit pas véritablement d’un projet ayant des conséquences sur plusieurs générations ;
- Il convient également de prendre en compte la nature des principaux avantages. Un tramway peut contribuer à réduire la pollution, ce qui pourrait justifier l’utilisation d’un taux plus faible. Cependant, ce n’est probablement pas l’impact principal du projet. L’avantage principal est souvent lié aux gains de temps et de confort pour les usagers ;
- Il faudra également considérer éventuellement le risque systémique du projet. Les avantages nets sont certainement positivement liés aux conditions économiques, ce qui pourrait justifier l’ajout d’une prime de risque ;
- Il est conseillé de présenter l’évaluation de l’avantage net au fil du temps, sans actualisation ;
- Il est également nécessaire d’effectuer une analyse de sensibilité de la VAN du projet par rapport au TAS. Il serait probablement utile de déterminer le taux de rendement interne du projet ;
- La recommandation devra également tenir compte des variations de la VAN et du taux de rendement interne du projet en fonction des autres paramètres déterminants de l’ACA.
Exercices
- Expliquez brièvement pourquoi le taux d’intérêt sur le marché des capitaux n’est pas nécessairement une bonne mesure du taux d’actualisation social.
- À partir des notions de dictature du présent et de l’avenir, expliquez les enjeux associés à l’actualisation de projets visant à réduire les émissions de gaz à effets de serre.
- Qu’est-ce que l’actualisation hyperbolique ?
- Veuillez expliquer succinctement l’intuition sous-tendant la formule de Ramsey.
- Expliquez brièvement les deux approches principales pour déterminer le taux d’actualisation social.
Bibliographie
Baumstark, L., Bonnet, J., Croq, A., Ducos, G., Meunier, D., Rigard-Cerison, A. et Roquigny, Q. (2013). L’évaluation socioéconomique des investissements publics. Commissariat général à la stratégie et à la prospective https://www.strategie.gouv.fr/
sites/strategie.gouv.fr/files/archives/CGSP_Evaluation_socioeconomique_17092013.pdf
Boardman, A.E., Moore, M.A. et Vining, A.R. (2010). The Social Discount Rate for Canada Based on Future Growth in Consumption. Canadian Public Policy, 36(3), 325-343. https://doi.org/10.3138/cpp.36.3.325
Boyer, M., Gravel, É., et Mokbel, S. (2013). The valuation of public projects: Risks, cost of financing and cost of capital. Commentary-CD Howe Institute, (388). https://acces.bibl.ulaval.ca/login?url=https://www.proquest.com/scholarly-journals/valuation-public-projects-risks-cost-financing/docview/1438025725/se-2
Gostner, C. et Ni, J. (2023). Guide de l’évaluation socioéconomique des investissements publics : Comité d’experts des méthodes d’évaluation socioéconomique des investissements publics. France Stratégie. https://www.strategie.gouv.fr/sites/
strategie.gouv.fr/files/atoms/files/fs-2023-guide-evaluation-investissements-publics-septembre.pdf
Green, L., Fry, A. F. et Myerson, J. (1994). Discounting of delayed rewards: A life span comparison. Psychological Science, 5(1): 33–36. https://doi-org.acces.bibl.ulaval.ca/
10.1111/j.1467-9280.1994.tb00610.x
Harberger, A. C. (1969). The Social Opportunity Cost of Public Funds. Western Agricultural Economics Research Council, The Discount Rate in Public Investment Evaluation, Denver, Col.
HM Treasury (2018). The Green Book: Central Government Guidance on Appraisal and Evaluation (p. 104). https://assets.publishing.service.gov.uk/government/uploads/
system/uploads/attachment_data/file/685903/The_Green_Book.pdf
Jenkins, G. et Kuo, C.-Y. (2007). The Economic Opportunity Cost of Capital for Canada – An Empirical Update (Working Paper No. 1133). Queen’s Economics Department. https://www.econ.queensu.ca/sites/econ.queensu.ca/files/qed_wp_1133.pdf
Montmarquette, C., et Scott, I. (2007). Taux d’actualisation pour l’évaluation des investissements publics au Québec (2007RP-02). CIRANO. https://cirano.qc.ca/files/publications/2007RP-02.pdf
Nordhaus, W. D. (2007). A Review of the Stern Review on the Economics of Climate. Journal of Economic Literature, 45(3), 686–702. http://piketty.pse.ens.fr/
files/Nordhaus2007b.pdf
Office of Management Bureau (2018). Discount Rates for Cost-Effectiveness Analysis of Federal Programs: Revision to Appendic C of OMB Circular A-94. https://www.federalregister.gov/documents/2018/02/08/2018-02520/discount-rates-for-cost-effectiveness-analysis-of-federal-programs
Ramsey, F. P. (1928). A Mathematical Theory of Saving, The Economic Journal 38(152), 543-559.
Rojas, F., López-Castro, M. A. et Júnior, R. P. (2023). Guide de l’analyse avantages-coûts des projets publics en transport routier, Partie 1 : Méthodologie. Ministère des Transports et de la Mobilité durable. https://www.transports.gouv.qc.ca/fr/entreprises-partenaires/entreprises-reseaux-routier/guides-formulaires/documents-gestionprojetsroutiers/guideaac-methodologie.pdf
Rojas, F., López-Castro, M. A. et Júnior, R. P. (2023). Guide de l’analyse avantages-coûts des projets publics en transport routier, Partie 2 : Paramètres (valeurs de 2019). Ministère des Transports et de la Mobilité durable. https://www.transports.gouv.
qc.ca/fr/entreprises-partenaires/entreprises-reseaux-routier/guides-formulaires/
documents-gestionprojetsroutiers/guide-avantages-couts-projets-publics.pdf
Stern, N. (2007). The Economics of Climate Change: The Stern Review. Cambridge University Press. https://doi-org.acces.bibl.ulaval.ca/
10.1017/CBO9780511817434
Tagne Kuelah, J.-R. (2016). L’évaluation du rendement d’une dépense publique : Un précis méthodologique à l’usage des évaluateurs de programmes du Ministère. Ministère de l’Économie, de la Science et de l’Innovation. https://www.economie.gouv.qc.ca/
fileadmin/contenu/publications/administratives/rapports/rendement_depense_publique.pdf
US Environmental Protection Agency (2010). Guidelines for preparing Economic Analyses (pp. 6-18). https://www.epa.gov/sites/production/files/2017-08/documents/
ee-0568-50.pdf
Différence entre la somme des avantages et des coûts en dollars de l’année de référence, obtenue à l’aide d’une actualisation.
Situation dans laquelle l’une des parties prenantes de la transaction détient plus d’informations pertinentes que l’autre. Cette disparité dans la distribution des informations peut conduire à des inefficacités sur les marchés.
Taux d’actualisation calculé de telle manière que la valeur actualisée nette (VAN) calculée avec ce taux s’avère nulle.
Étude de l’évolution de la valeur actualisée nette lors de changements des paramètres et des prévisions. Il existe trois types d’analyse de sensibilité : par paramètre, par scénario et par simulation de Monte-Carlo.
Processus d’application de formules mathématiques, comportant le taux d’actualisation social comme paramètre clé, pour calculer la valeur actuelle (exprimée en monnaie de l’année de référence) des avantages ou des coûts qui seront réalisés dans l’avenir. Cette technique permet de comparer des coûts et des avantages qui se manifestent à différents moments dans le temps, en tenant compte du coût d’opportunité des ressources investies dans un projet. Par essence, l’actualisation reflète le rendement auquel la société renonce en orientant ses ressources vers un investissement donné, plutôt que vers la meilleure alternative possible.
Le coût de renonciation du capital, également connu sous le nom de « coût d’opportunité du capital », désigne le rendement qu’un investisseur sacrifie en choisissant d’investir dans un projet particulier plutôt que dans une alternative jugée équivalente en termes de risques.
Établit dans quelle mesure les avantages sociaux d’un projet excèdent les coûts sociaux.

